基于機器學習的基坑變形預測研究
楊建新 唐海英
(湖南省核工業(yè)地質局三0二大隊,湖南郴州 423000)
0.引言
隨著城市化建設的高速發(fā)展[1],地下空間的開發(fā)利用不斷深化,基坑的開挖規(guī)模日益增長。與此同時,在基坑開挖的過程中,其往往會對其周邊環(huán)境產生影響,影響周邊建筑物及基坑自身安全。而基坑工程在大型工程建設當中,能夠保證周圍土體穩(wěn)定性,因此具有重要意義。在進行基坑建設當中,基坑的變形預測及其監(jiān)測顯得至關重要[2]。
一般而言,常見的基坑變形研究方法,主要包括數值模擬[3]、理論計算[4]以及智能算法預測[5]等。在數值模擬方面,Liu Haiming等[6]利用基于有限差分算法的FLAC3D軟件,選用2種本構模型,對地面沉降進行了模擬,通過與現場監(jiān)測數據進行對比,研究了基坑開挖影響范圍。劉冰冰[7]采用ABAQUS數值軟件,對西安地鐵四號線基坑工程沉降進行了模擬分析,研究了基坑開挖降水對相鄰建筑物的影響。在理論計算方面,國外學者Peck[8]基于大量的基坑工程數據,提出了基坑地表沉降的計算公式,并得到了廣泛應用。此后,段紹偉等[9]根據長沙市地鐵開挖的實測數據,采用回歸分析方法對Peck沉降計算公式進行了修正。數值模擬及理論計算為現場基坑建設提供了理論指導,但是由于基坑變形的復雜性及隨機性,導致現場實際沉降與理論計算具有一定的偏差,而智能算法能夠避開基坑變形的內在機理,具有良好的預測能力,目前已經成為基坑變形預測的主要技術手段[10]。
基于此,本文將主要利用隨機森林、決策樹、支持向量機3種機器學習算法,結合上海某深基坑實測數據,對基坑的變形量進行預測,分析了基坑沉降的影響因素。
1.機器學習算法介紹
1.1 決策樹算法
決策樹算法是目前最常見的機器學習算法之一,其通過信息熵作為判別標準,將決策樹葉節(jié)點上的值為輸出樣本信息,而非葉節(jié)點上的值為數據樣本中某個屬性的劃分點,樣本數據根據該屬性上的不同分割點而被劃分為多個子數據集[11]。建立決策樹的核心在于非葉節(jié)點上屬性的選擇,即如何選擇適當的屬性及屬性的分割點對樣本數據進行劃分。
對于回歸問題,常用的算法為CART決策樹算法。對于給定的訓練T={(x1,y1),(x2,y2),...(xn,yn)},根據訓練數據集中的幾個或者全部特征,按一定的方法對樣本數據進行分割,從而建立相應決策樹,使得決策樹中葉子結點上的值與訓練樣本中的值相等或接近。決策樹建立過程中的核心問題是非子葉節(jié)點上特征的選擇。假如選擇訓練集T中的j號特征中的s分量作為分割訓練集的閾值,原數據集將分為R1={x|Rj≤s},R2={x|Rj>s}兩部分,分割后模型的輸出值與實際y值的均方誤差可表示為:
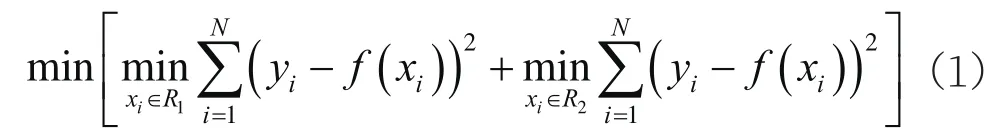
式中,f(xi)代表模型的輸出值,其越接近實際值y,說明模型精度越高。
1.2 隨機森林算法
隨機森林的基本思想是通過Bagging集成,將多個弱決策樹求解結果取平均值,從而獲得具有較高精確度和泛化性能的算法[12]。模型如圖1所示,通過Bootstrap重采樣技術,從原始訓練數據集D中有放回地重復隨機抽取k個樣本,生成新的訓練數據集,然后基于新生成的k個訓練集建立k顆決策樹,將這k顆決策樹組成隨機森林。隨機森林的計算結果等于每顆決策樹的計算結果求的平均值。
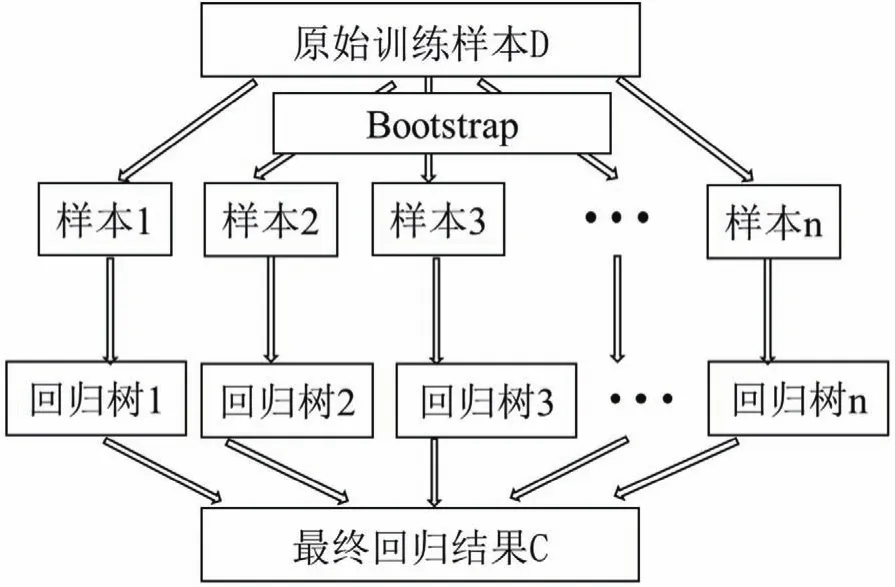
圖1 隨機森林示意圖
1.3 隨機森林算法
支持向量機是將實際問題通過非線性變換Φ(x)轉換到高維的特征空間,再利用各種優(yōu)化算法求得最大分類間隔,以使樣本點能夠線性可分地轉換到所得到的高維空間。在這些樣本點中,有一部分位于最大分類間隔的超平面之上,即支持向量點[13]。
支持向量機原理如圖2所示,設待求解的數據集為(x1,y1),(x2,y2)…(xn,yn),x∈R,y∈R,i=1…N。xn為輸入數據,y為輸出數據,通過使所有的樣本點離超平面的總偏差最小,此時可建立如下關系式:
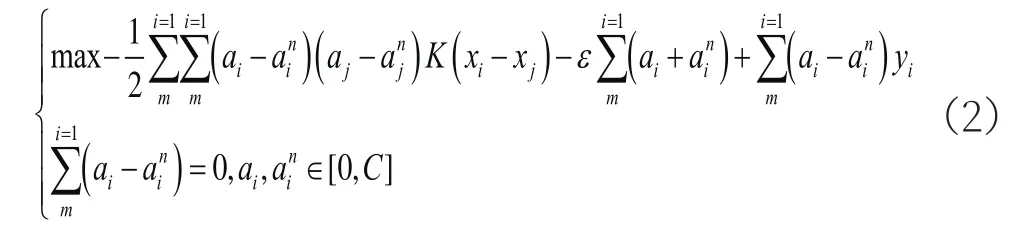
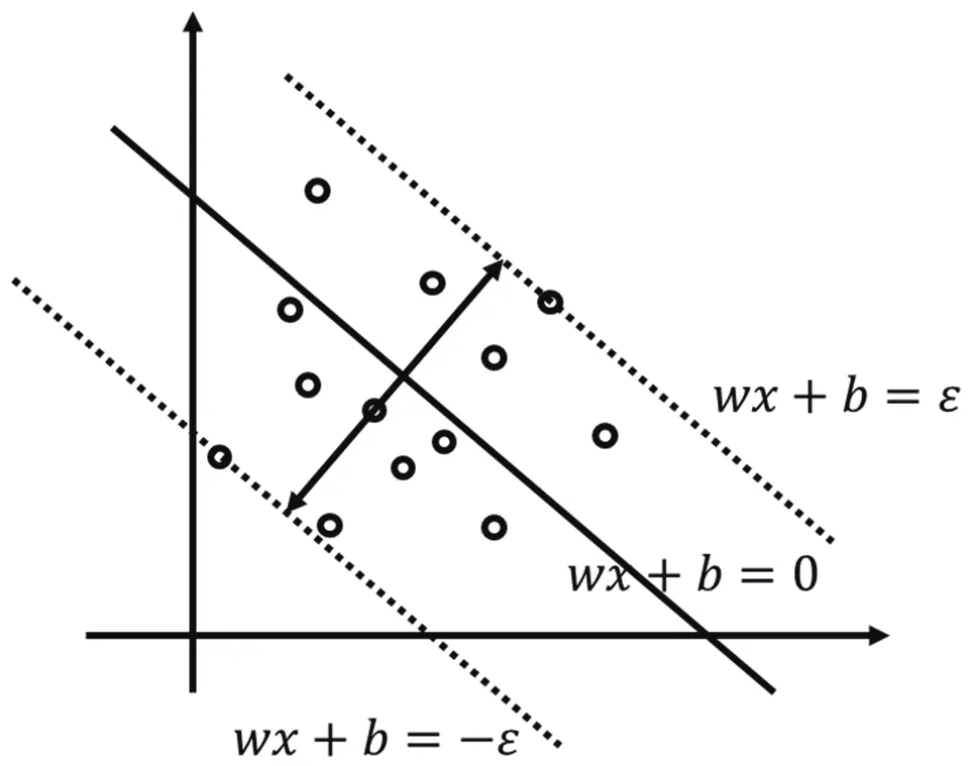
圖2 支持向量機示意圖
式中,C、ε為懲罰因子和不敏感損失參數,w,b最優(yōu)決策函數的函數系數,其映射關系為y=wTΦ(x)+b,K(xi,xj)為核函數,常見的核函數包括線性核函數、多項式核函數、徑向基核函數等。通過KKT對線性規(guī)劃進行求解,其中ai、ain為拉格朗日乘子,系數ai-ain不為0,因此映射關系可以轉換為:
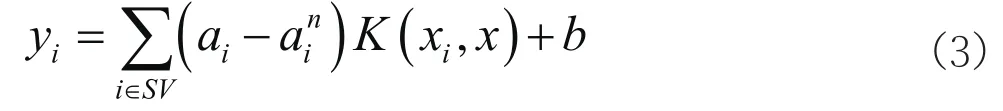
2.基于機器學習的基坑沉降變形預測
2.1 工程分析
基坑開挖對于周邊地面變形的影響不可忽視,其往往是多因素的共同作用的結果。主要包括:施工工況、巖土層參數、支護結構剛度以及支撐形式等,每種因素對于周邊地面變形的影響程度及方式不同,應用傳統的理論計算方法,難以考慮多種因素建立準確的基坑沉降預測模型,機器學習方法為此提供了可靠途徑。
以上海某基坑工程為例,在現場施工過程中,通過記錄基坑開挖深度、開挖面以上地層內摩擦角值、土體粘聚力值、土體重度、地層滲透系數、監(jiān)測點距離及監(jiān)測點沉降的實測值。圖3為選取的輸入變量與基坑變形量的Pearson相關系數圖,可以衡量變量之間的線性相關,數值的取值范圍為[-1,1]。其中,-1表示為負相關,1表示為正相關。當數值越接近1或-1時,表示相關度越強,越接近0時,則表示相關度越弱。可以看出,輸入變量與輸出變量之前存在一定的相關性。
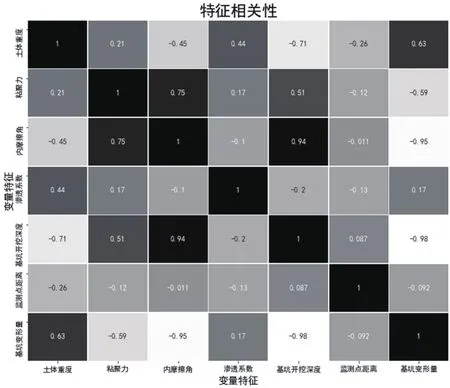
圖3 輸入變量與輸出變量相關系數圖
基于此,本文選取100組監(jiān)測數據作為訓練樣本和測試樣本建立預測模型,選取的監(jiān)測數據涵括開挖前、開挖中及基坑施工后全周期,隨機抽取80%的數據作為訓練集,剩下20%的數據作為測試集,分別基于決策樹算法、隨機森林算法及支持向量機算法進行模型預測。
2.2 機器學習超參數調整及其評價指標定義
通過調整模型超參數,以獲得最優(yōu)化模型,提高機器學習模型的預測準確性。本文基于網格搜索交叉驗證方法(GridSearchCV)進行超參數調整[14]。如圖4所示為5折交叉驗證示意圖,其原理為通過將超參數數據集分為n個子集,以一個子集作為驗證集,其余n-1個子集作為訓練集,得到模型的結果,并通過循環(huán)變換驗證集,重復上述過程,選取模型表現最優(yōu)的超參數數據集作為模型的超參數。

圖4 交叉驗證示意圖
本文采用擬合優(yōu)度R2和均方根誤差RMSE統計指標作為本文機器學習預測模型精確度的評價指標,其定義如下式所示:
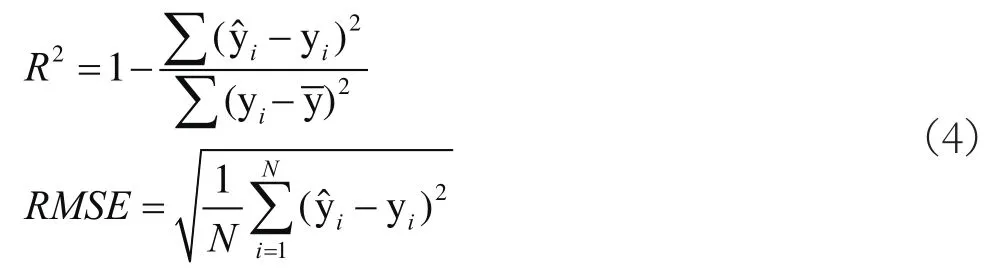
2.3 預測結果及分析
在機器學習中,使用網格搜索交叉驗證獲得的最佳超參數組合進行建模,各模型在測試集上的性能表現見表1所示。可以看出,支持向量機具有較差的預測效果,隨機森林和決策樹算法具有較高的預測精度,其擬優(yōu)度都超過了0.9,且均方根誤差在2以下。其中隨機森林算法預測能力最好,這主要是由于輸入數據與輸出數據具有高度非線性,因此集成算法能夠具有較高的表現能力。
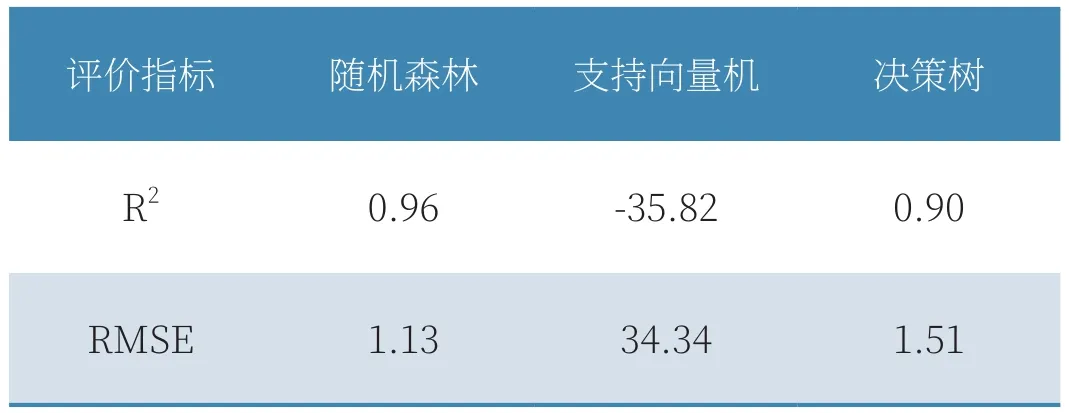
表1 機器學習預測結果對比
通過上述分析,利用3種機器學習模型對整個數據集進行建模分析,最終的結果如圖5所示。可以看出,基于隨機森林模型和決策樹模型的預測值均較好地分布在理想擬合線附近,其最大相對誤差為0.35%,具有較高的穩(wěn)定性。而基于支持向量機模型的預測值則表現較差,其最大相對誤差為10.34%,難以滿足工程實際要求。總的來說,不同機器學習算法,由于其內核計算方法的差別,在同一工程數據的預測應用中表現出精度差異。
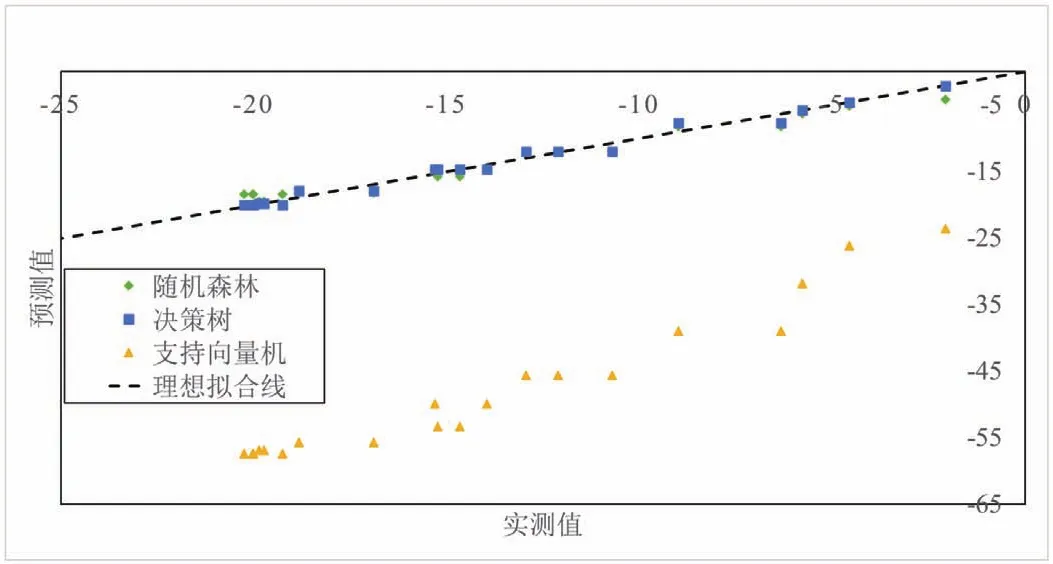
圖5 隨機森林預測結果
基坑周邊沉降實測值和基于隨機森林模型的預測值如表2所示,可以看出,對于本文所研究的基坑,基于隨機森林模型的預測結果雖有一定的波動,但仍在可接受的范圍之內,其相對誤差范圍為0.13%~2.01%,平均相對誤差為0.97%,對于基坑變形預測來說其精度滿足要求[15]。
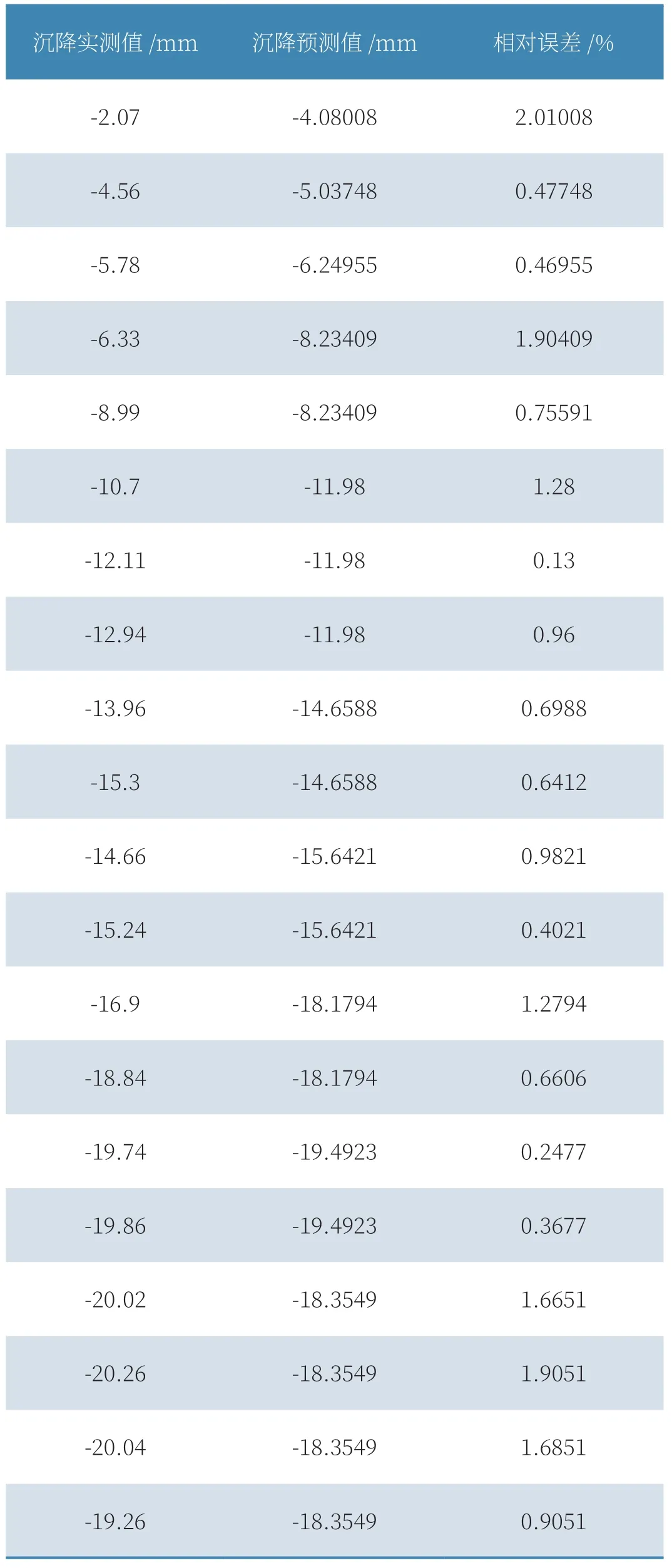
表2 位移實測值與預測值的比較
2.4 影響因素分析
影響基坑沉降的因素很多,但是不同的因素對沉降的影響程度不一樣。在機器學習算法中,函數“feature_importance_”對各影響因素的重要性給出了定量解釋,具體數學過程如下[16]:
(1)對每一顆決策樹,建立決策樹前將數據集分為訓練集和預測集,選擇沒有參與建立決策樹的預測集數據進行預測,計算出預測值與試驗值的誤差,記為err1。(2)隨機對預測集數據中樣本的影響因素(因變量)X加入噪聲干擾(即隨機改變樣本在特征X的值),再次計算預測值與試驗值之間的誤差,記為err2。(3)假設森林中有N棵樹,則影響因素(因變量)X的重要性為:
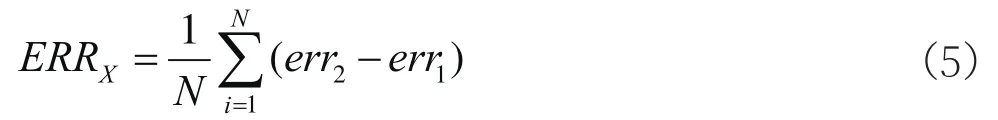
當加入隨機噪聲后,模型的精度會發(fā)生變化(即err2改變),err2改變的幅度即反映出輸出結果對X變量的敏感性,假如X變量對結果無影響,則err2與err1相等,即是ERRX等于0,ERRX越大,說明X變量對于樣本的預測結果有很大影響,進而說明該特征的重要程度比較高。進一步基于隨機森林模型分析了各影響因素對于基坑沉降的敏感性影響如圖6所示。圖6中所有的重要性系數總和為1,從中可以看出內摩擦角、粘聚力和檢測點距離的相對重要性系數分別為0.245、0.231和0.22,為所有影響因素中較高的3個得分值。在隨機森林模型中,影響因素的重要性排名為內摩擦角>粘聚力>監(jiān)測點距離>土體重度>基坑開挖深度>土體滲透系數,證明了土層本身性質對于基坑的沉降影響至關重要。
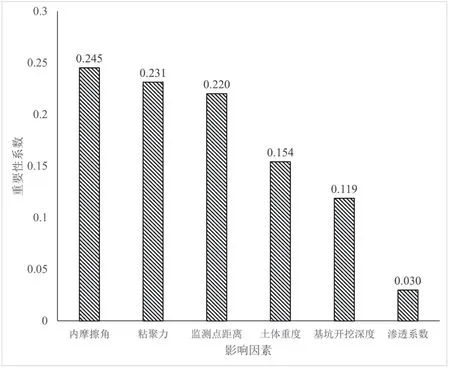
圖6 隨機森林模型生成的特征重要性
3.結論
本文基于機器學習中的決策樹、隨機森林和支持向量機算法對基坑沉降進行預測,得出主要結論如下:
(1)傳統的模型一般難以考慮基坑的復雜性,本文基于基坑實測數據,建立了基坑沉降預測的機器學習模型,并通過與實測數據進行對比分析,結果表明基于隨機森林的預測模型表現優(yōu)于其他2種模型,其最大相對誤差為2.01%。(2)影響因素分析結果表明,眾多影響因素中,內摩擦角對基坑沉降的影響最顯著,但土層力學性質等特征的影響較為平均,而土層滲透系數對于基坑沉降的影響較小。本文研究結果為基坑工程建設提供有益參考。

