使用時序技術對云平臺基礎費用數據的波動性分析
于曉雷


摘要:企業上云已經成為提高企業IT水平、增加IT效率的有效方式,本文以云平臺管理中的基礎費用為研究對象,結合現代統計方法中的ARIMA模型,綜合運用現代統計方法,在對云平臺基礎費用結合ARIMA模型進行分析的基礎上,實現對未來基礎費用的預測和分析,為企業的決策提供可參考的方法和數據。本文擬從針對云平臺數據進行分析預測的實際需求;目前學界使用ARIMA算法進行時序分析的現狀和成果;傳統和現代的一些主流的時序數據分析技術和方法;針對云平臺的基礎費用、使用時序預測技術的分析、預測和校驗四部分進行探討。
關鍵詞:時序預測;ARIMA模型;云平臺;基礎費用預測
中圖分類號:TP311? ? ? 文獻標識碼:A
文章編號:1009-3044(2021)17-0028-03
開放科學(資源服務)標識碼(OSID):
1 序言
SAP云平臺是基于CloudFoundry技術建立的新一代PAAS平臺,可以幫助用戶快速實現SAP產品的功能擴展和無縫集成,支持用戶業務創新。作為SAP云平臺的運營方,為了保障服務的高效性,節省云平臺的運營成本,需要建立精細化、體系化的服務級云成本優化工具,為運維人員提供可視化的云成本分析和智能化的資源消耗預測和優化建議,并最終實現對資源的一鍵式優化執行,達到自動化、智能化降本增效的效果。
在實際生產實踐中,數據的波動性分析是很常見的一項工作。SAP云平臺在阿里云是采用了“按使用的時長后付費+ 預留實例資源”的模式,這種模式需要提前向阿里云申請后付費配額,一旦用量超過信用額度限制,將無法實現基礎資源擴容。因此,在這種情況下,提前預測服務用量及其阿里云資源消耗量就顯得比較重要。
時間序列分析是一種在各個生產領域有著廣泛使用的數據預測和分析方法,該方法可以根據時間序列數據建立對未來數據進行預測是時序模型,并對未來的數據有著比較好的預測效果和結論,對于科學決策有著比較好的參考和輔助決策效果。本文研究探討了如何使用時序分析技術來對云平臺基礎費用量進行預測,以便根據預測銷量,及時調整技術方案,并做出可行的商業對策,為云平臺更高效、平穩地運行打下良好的基礎。
2 時序數據分析方法
2.1 時間序列數據分析的方法
時間序列分析的一個主要目的就是根據已有的歷史數據對未來進行預測,時間序列含有不同的成分,比如趨勢、季節、周期性和隨機性等。對于一個具體的時間序列,它可能只含有一種成分,也可能同時含有及幾種成分,二者所用的預測方法是不同的。確定時間序列的成分,可以從繪制時間序列的線形圖入手,或者利用回歸分析擬合一條趨勢線,然后對回歸系統進行顯著性檢驗。如果回歸系數顯著,就可以得出線性趨勢顯著的結論。
2.2 現代的時間序列分析技術
現代的時間序列分析典型代表是由Box-Jenkins提出的一系列預測方法,包括:AR模型、MA模型、ARMA模型、ARIMA模型等。
1)AR模型,自回歸模型,其優點是利用自身的歷史數據進行預測,所需的數據不多。缺點是收到了一定限制,要求自回歸系統必須小于0.5,否則不宜采用。這種模型只適合應用于預測與自身前期密切相關的時間序列數據,不能預測受外界影響較大的數據
2)MA模型,滑動平均模型,是模型參量法高分辨率譜分析方法之一,也是現代譜估計中常用的模型。通常用于處理正弦信號,多用于機械零件的故障診斷和分析。
3)ARMA模型,自回歸滑動平均模型,是研究時間序列的最重要的方法之一,屬于AR模型和MA模型的混合模型。
4)ARIMA模型,差分整合移動平均自回歸模型,是時間序列預測的現代方法之一。
3 使用ARIMA模型進行時序數據分析
3.1 數據來源及其分析選型
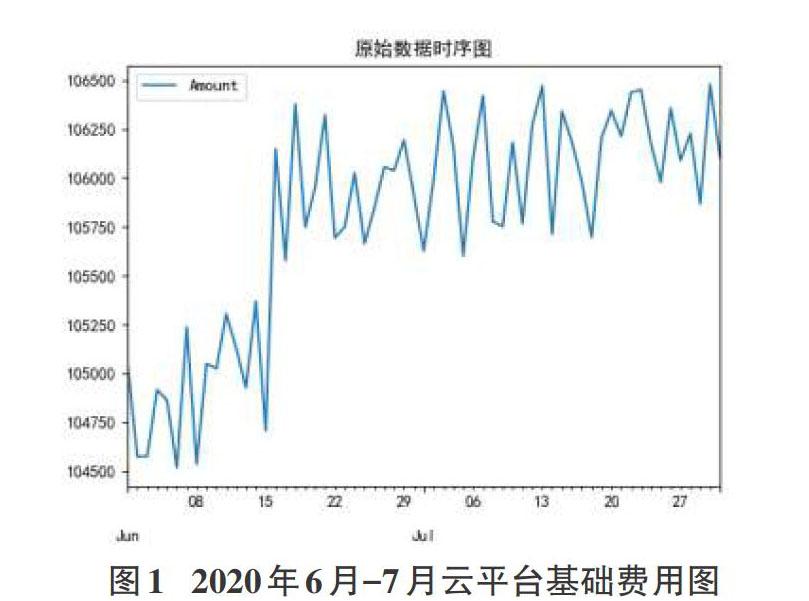
本文的數據來自云平臺的基礎費用數據,以未經過RI(折扣優惠)的原始數據作為依據,按天排列的等時數據,分別以日期和對應的基礎費用金額為橫軸和縱軸坐標,進行繪圖,如下:
根據圖1顯示的數據,可以發現2020年6月-7月云平臺基礎費用總體趨穩,其間有若干小幅波動和一個比較明顯的波動。長期趨勢基本平穩,但是小幅向上。
根據基礎費用圖形分析,本文擬采用基于ARIMA模型的時間序列分析方法來預測未來一段時間的平臺基礎費用。ARIMA模型只能處理平穩時間序列,所以使用ARIMA模型對序列進行處理的時候,首先需要將非平穩時間序列轉化為平穩序列,然后進一步通過對因變量的滯后項進行回歸,以及對隨機誤差進行回歸處理從而建立起來預測模型。該模型的數學表達式為:ARIMA(p,d,q)。
3.2 ARIMA模型對數據的處理、分析以及實證
3.2.1 原始數據穩定性檢驗
在對基礎費用進行預測和分析的時候,前提是要求數據平穩,因此在對數據進行分析和處理之前首先要確定時間序列數據的平穩性。由圖1可知,數據存在一定的小幅波動,2020年6月15日有稍大幅度波動,因此可以采用差分處理方法使數據保持平穩性。而檢驗序列數據是否平穩,可以采用時序圖檢驗,自相關檢驗,單位根檢驗等方法來檢驗。
1)時序圖檢驗,從圖1中可以發現,數據為非平穩系列,有一定幅度波動,并有向上趨勢。判斷為非平穩時序數據序列。
2)ADF檢驗,也即單位根檢驗,來對數據的平穩性進行分析。本文使用Python中的statsmodels模塊來檢驗原始數據的平穩性。
結果顯示,原始序列的ADF檢驗P值為:0.2144471525 5903202,顯著大于0.05,因此可以判斷該序列為非平穩序列。
3)自相關和偏自相關檢驗:這里同樣可以使用Python代碼,來對數據序列進行自相關和偏自相關的檢驗,所得原始數據的自相關圖和偏自相關圖如下:
觀察圖2的自相關圖和圖3 的偏自相關圖,可以發現:自相關圖顯示自相關系數波動和振幅較大,呈倒三角分布,說明序列的相關性非常強,屬于非平穩序列。同樣偏自相關圖也有類似特點。
3.2.2 原始數據白噪聲檢驗
ARIMA模型對于時序數列的處理,必須是平穩且非白噪聲序列,所謂白噪聲,指完全隨機,在任何兩個時間點上的隨機變量均沒有任何關聯,沒有任何可以發現和利用的動態規律,不能通過歷史數據推斷和預測未來數據的數據系列。本文可以通過statesmodel中的acorr_ljungbox方法來判斷原始處理的數據系列是否為白噪聲。
結果顯示,原始序列的白噪聲的p值為5.21711013e-08,不屬于白噪聲系列。
3.2.3 原始數據的一階差分處理
綜上結果,需要對數據進行平穩性處理,擬先采用差分方法。差分變換為通過對數據序列逐項進行相減來消除序列數據中的線性趨勢。對數據進行差分,可以嘗試采用一階差分,如果線性趨勢沒有消除,則可以繼續采用二階差分,具體公式如下:
同樣可以使用Python代碼進行一階差分,print(u'差分序列的ADF檢驗結果為:', ADF(Difference_data[u'amount差分'])) #平穩性檢測。
3.2.4 一階差分數據的穩定性校驗
對于一階差分數據,同樣可以進行時序圖檢驗、ADF檢驗以及自相關、偏自相關檢驗。
1)觀察時序圖(見圖4),可以發現,數據序列趨于平穩,圍繞均值做平緩波動,已經屬于平穩系列。
2)自相關檢驗
觀察自相關圖(圖5)和偏自相關圖(圖6),可以發現自相關和非自相關都有著較強的短期相關性,大部分值位于置信區間內。
綜上所述,可以明顯判斷出來,一階差分之后的數列是平穩的。
3.2.5 一階差分數據的白噪聲檢驗
根據前述,由于ARIMA模型要求時序數列必須是非白噪聲序列,因此我們還需要對差分之后的數據進行檢驗,確認差分之后的數據為非白噪聲時序數據。本文同樣通過statesmodel中的acorr_ljungbox方法來判斷差分處理的數據系列是否為白噪聲。
結果顯示,差分序列的白噪聲的p值為5.61810719e-06,則經過差分處理之后的數據系列不是白噪聲系列。
3.2.6 AMRIA模型預測及結論
經過差分處理之后,可以發現時間序列數據的平穩性已經符合ARIMA模型的要求,接下來要確定p、q的參數值,結合一階差分后的ACF和PACF的圖形觀察,可以初步確定:
ACF在一階之后截尾,PACF在1階之后拖尾,則可以暫定p=1,q=1。接下來,使用代碼得出了5天的預測結果(包含預測結果、標準誤差、置信區間信息):
(array([106297.67658519, 106280.45417936, 106315.839 85059, 106338.01452291,
106363.50675599]), array([322.99742609, 324.82316709, 341.95101241, 353.25939582,
365.35637135]),array([[105664.61326296,106930.73990742],
[105643.81247051, 106917.09588821],
[105645.62818179, 106986.05151938],
[105645.63882989, 107030.39021592],
[105647.42142661, 107079.59208536]]))
這里獲得的是一個元組,元組中一共有三個元素,分別是:預測結果、標準誤差、置信區間。
3.3 ARIMA預測模型的數據檢驗
本文以八月份真實基礎費用金額的前五天數據作為對比和驗證數據,針對預測數據進行對比和雅正,考察數據模型的擬合度。
針對表2數據進行檢驗,可以發現表2的真實基礎費用均在預測的95%的置信區間內,并且預測均值和實際基礎費用發生額相差很小。故可以認為ARIMA(1,1,1)模型能夠滿足實際企業云平臺相關預測的需要。
4 結語
云平臺基礎費用具有一定的波動性,同時具有等時的時分性,同時數據之間具有相互的獨立性,對此,本文采用統計學的方法建立了ARIMA模型,探討了通過時間序列的ARIMA模型針對基礎費用進行預測的可行性,并結合歷史數據以及Python中的statsmodels模型對歷史數據進行了分析和處理,得到了歷史數據的預測結論。
期待本文對企業的基礎費用預測和銷售策略選擇,以及產業優化和布局的決策能提供一定的輔助手段,可以讓企業有針對性地拓展云業務,為企業在云業務的大潮中站穩腳本提供一個有效的技術方法和手段。
參考文獻:
[1] 賈俊平,等.統計學(第六版)[M].北京:中國人民大學出版社,2015.
[2] 姚加林,皮珊.基于ARIMA模型的高鐵浮動票價與票額分配優化方法[J].鐵道科學與工程學報,2020,17(7):1655-1661.
【通聯編輯:李雅琪】

