同構式解題舉隅
2021-08-05 08:27:32蔣滿林
數理化解題研究 2021年16期
蔣滿林
(福建省古田縣第一中學 352200)
一、預備知識
指對混雜恒等式:xex=lnex·ex=tlnt(t=ex);xlnx=elnx·lnx=tet(t=lnt).
這兩個恒等式就是通常所說的指對混雜同構式,簡稱同構式,它在解決某些指、對函數混雜問題往往能收到時事半功倍的效果,下面結合例子說說同構式的具體應用.
二、同構式解題
1.利用同構式求參數范圍
例1(2020山東21,海南22題)已知函數f(x)=aex-1-lnx+lna.
(1)略;
(2)若f(x)≥1,求a的取值范圍.

評注構造同構式ex-1+lna+x-1+lna≥x+lnx=elnx+lnx,再利用函數g(t)=et+t的單調性進行解題,避免了遇字母就討論的基本思路,創新思維視角、簡化過程計算,提高解決問題的能力.
2.利用同構式求參數最值



3.利用同構式證明不等式
例3 已知函數f(x)=2x-lnx.
(1)求函數f(x)的單調區間;


4.利用同構式計算函數值
例4 已知x0是函數f(x)=x2ex-2+lnx-2的零點,計算e2-x0+lnx0的值.


三、變式練習

2.已知函數f(x)=2ae2x-lnx+lna,若f(x)≥0恒成立,求實數a的最小值.
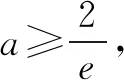
附參考解答


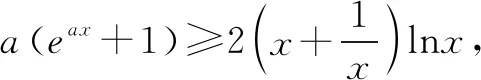
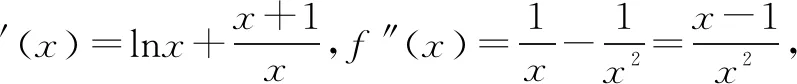
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
中等數學(2022年2期)2022-06-05 07:10:50
中學生數理化·七年級數學人教版(2021年11期)2021-12-06 05:38:48
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10

