高中生數(shù)學建模能力培養(yǎng)途徑的思考

張樹懷

(江蘇省泰州市姜堰區(qū)溱潼中學225508)

高中數(shù)學教學中培養(yǎng)學生的建模能力，不僅能提高學生運用數(shù)學知識解決實際問題的能力，而且有助于促進學生核心素養(yǎng)的提升，因此，應做好高中數(shù)學建模知識總結，結合自身教學經(jīng)驗，積極尋找培養(yǎng)學生建模能力的有效途徑，將培養(yǎng)工作融入到相關教學環(huán)節(jié)之中，促進學生建模水平與建模能力的明顯提升.

一、注重建模基礎知識講解

建模對學生的各項能力要求較高，因此教學中應注重為學生講解建模基礎知識，使學生掌握建模的步驟與細節(jié)，為其靈活應用于解題中做好鋪墊.一方面，講解教材中模型內(nèi)容時應注重運用多媒體技術，如結合多媒體課件講解二次函數(shù)、指數(shù)函數(shù)、冪函數(shù)等，使學生認識到其都屬于數(shù)學模型，更好的吸引學生的注意力.同時，注重在課堂上與學生積極互動，營造寬松活潑的課堂氛圍，激發(fā)學生學習數(shù)學模型的積極性，尤其互動過程中學生表現(xiàn)較為積極，正確回答出提出的問題時應注重給予學生鼓勵，使其嘗到學習數(shù)學建模知識的成就感，更加積極主動的投入到數(shù)學建模學習中.另一方面，課堂上注重給學生留下一定的時間，要求學生總結數(shù)學建模的步驟，思考建立數(shù)學模型時的一些細節(jié)，掌握扎實的數(shù)學建模理論.

最終學生通過回顧所學，認真的討論得出構建數(shù)學模型時，可按照以下步驟進行：實際問題→建立數(shù)學模型→得到數(shù)學結果→解決實際問題.其中為保證構建模型的正確性，學生認識到需要認真審題，充分理解題意，對題干描述進行抽象，找到參數(shù)之間的關系，聯(lián)系所學數(shù)學知識構建模型，尤其應保證數(shù)學模型的參數(shù)范圍應符合實際.

二、做好數(shù)學建模過程示范

高中數(shù)學建模教學中為給學生留下深刻的印象，積累建模的經(jīng)驗技巧，靈活運用所學解決實際問題，應注重結合學生所學做好數(shù)學建模過程的示范.一方面，為學生示范時應注重選擇學生感興趣或較為熟悉的問題情境.建模時應注重與學生一起分析，使其親身體會建模過程，明白如何將實際問題與所學數(shù)學知識建立聯(lián)系.另一方面，認真板書建模過程，并為學生講解建模的技巧，促進學生建模能力的進一步提高.如在講解指數(shù)函數(shù)時，圍繞以下實際問題情景為學生示范數(shù)學建模過程：

例如，某種儲蓄的月利率為0.36%，今存入本金100元，求本金與利息的和y(元)與所存月數(shù)x之間的函數(shù)關系，并計算5個月后的本息和(不計復利)；按復利計算利息的一種儲蓄，本金為a元，每期利率為r，存期為x，寫出本利和y隨存期x變化的函數(shù)式，若存入本金1000元，每期利率為2.25%，試計算5期后的本利和.

題目中已經(jīng)給出y、x，建模過程就是尋找其關系的過程，結合所學的利息、本金、利率關系不難構建數(shù)學模型.因為利息=本金×月利率×月數(shù)，因此可構建一次函數(shù)模型y=100+100×0.36%×x，則當x=5時易得y=101.8元.如按復利計算，可與學生一起分析1期、2期、3期的求解過程，最終歸納出指數(shù)函數(shù)模型.當本金為a時，1期后的本利和y1=a+a×r=a(1+r)；2期后的本利和y2=a(1+r)+a(1+r)×r=a(1+r)2；3期后的本利和y3=a(1+r)3；…則x期后的本利之和為y=a(1+r)x，將a=1000，r=2.25%，x=5代入得到y(tǒng)=1000×(1+2.25%)5=1117.68.

三、及時進行課堂建模訓練

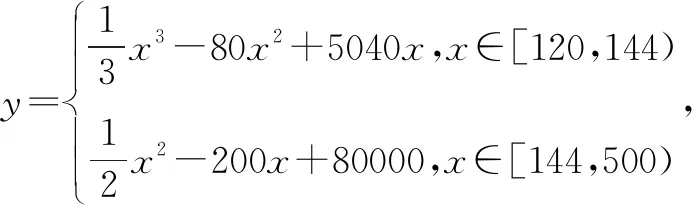
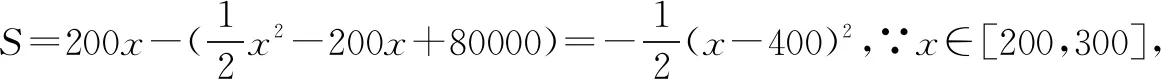
四、積極拓展數(shù)學建模能力

高中數(shù)學教學中為更好的培養(yǎng)學生的數(shù)學建模能力，應注重結合學生實際創(chuàng)設新穎的問題情境，拓展學生的數(shù)學建模視野與能力，提高其數(shù)學建模過程中思維的靈活性.一方面，平時做一個有心之人，注重積累生活中與數(shù)學相關的情境，進行巧妙的設計后在課堂上展示給學生，要求學生構建數(shù)學模型進行作答.另一方面，為提高學生建模的積極性，可將班級學生分成若干小組，在小組間開展數(shù)學建模比賽活動，比一比看哪個小組最先正確的構建出數(shù)學模型、得出正確結果，在課堂上給予表揚，激活數(shù)學課堂的同時，增強學生的合作意識以及集體榮譽感.

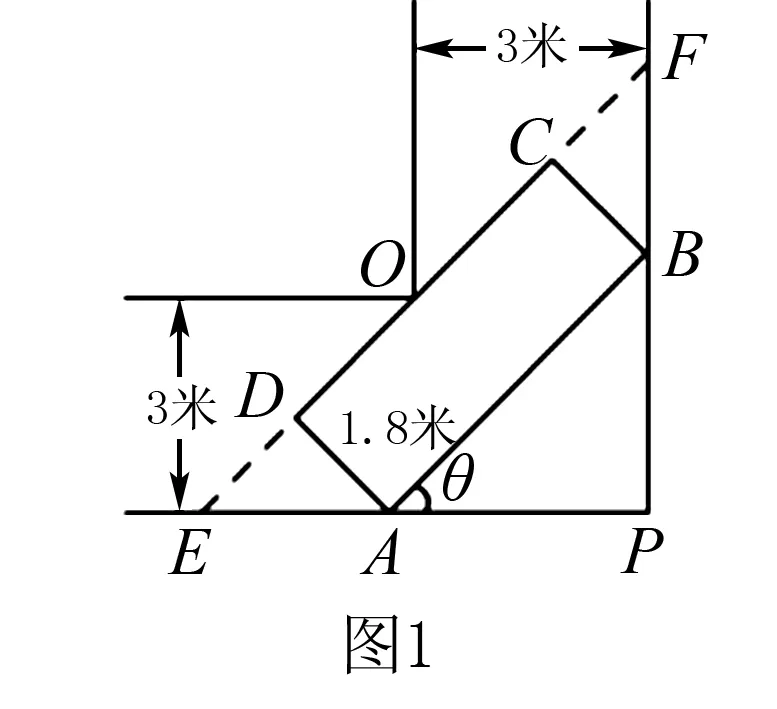
例如，一車庫有一條直角拐彎車道，平面圖如圖1所示，設∠PAB=θ，車道寬3米，現(xiàn)有一輛1.8米寬，4.5米長水平截面可視為矩形的小汽車，問能否順利的通過該拐彎車道？

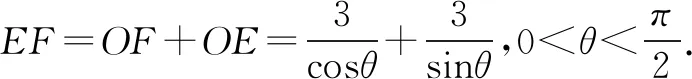
總之，高中數(shù)學教學中為培養(yǎng)學生的數(shù)學建模能力，平時應注重相關教學理論的學習，認真總結自身教學經(jīng)驗，結合學生實際情況尋找切實可行的培養(yǎng)路徑，并在教學中積極的實踐，做好相關培養(yǎng)環(huán)節(jié)的優(yōu)化與調(diào)整，使學生既牢固掌握數(shù)學知識，又促進其數(shù)學建模能力的顯著提升.