借助函數思想 解答數學難題

戴涓涓

(江蘇省南通市海門四甲中學 226100)

函數思想是解決數學問題的一種慣用思想方法，運用函數思想處理的題目往往有著共同屬性，那就是定量和變量之間的聯系.在高中數學解題教學中，函數思想占據著異常重要的地位，教師可根據題目實際情況指導學生靈活運用函數思想，使其將函數的性質與解題當作主要解題思路，把兩種不相干的知識聯系在一起，促使他們快速、正確的解答數學難題.

一、借助函數思想解答方程難題

高中生從小學時期就開始接觸到方程求解類的題目，一開始難度一般，隨著教育階段的提升，解方程的難度系數越來越高，對他們的知識基礎與思維方式也要求更高.在高中數學教學中，方程問題的困難程度與復雜性為學生帶來一定的困擾，教師可指導他們借助函數思想解答方程難題，根據方程中的未知量和已知量建立函數關系，使其迅速理清解題思路.

例1在求解方程lgx+x=2時，已知方程的一個解是x1，10x+x=2的解是x2，求解x1+x2的值.

解析假如按照常規方程法需對兩個式子分別解答，直接處理指數函數10x與對數函數lgx的計算量比較大，教師應指引他們仔細觀察這兩個方程式的基本結構，發現能使用指數函數與對數函數的圖象性質求出答案.又如：解方程(x2-x+1)5-x5+4x2-8x+4=0.分析：題目中是一個一元五次方程，先變形再采用函數性質解決起來比較容易.解：原式變形(x2-x+1)5+4(x2-x+1)=x5+4x，因為函數f(t)=t5+4t在R上單調遞增，又因為f(x2-x+1)=f(x)，則x2-x+1=x，解得x=1，即原方程有唯一實數解為x=1.

在高中數學處理方程問題時，學生運用函數思想通常可以便捷、快速的求出答案，使他們解題思路變得清晰起來，不僅能夠降低解方程的難度，還可以提升解方程的質量與效率.

二、用函數思想解答不等式難題

高中數學教學中的不等式問題，一般是通過>、≥、<、≤等數學符號建立的不平等邏輯關系式，在高考中也占據著一定的分值.面對不等式中的難題，高中數學教師可指導學生使用函數思想建立出合理的函數邏輯關系，把不等式問題轉變成函數問題，再通過解方程的常規手段將不等式的右半部分變成0，最后求出不等式的左半部分，輔助他們解答難題.

例2已知a、b、c∈R，且它們的絕對值均比1小，求證ab+bc+ca+1≥0.

解析學生在看到這道題目時，往往只關注已知條件，發現無從下手，假如換一個角度分析，利用函數思想把證明ab+bc+ca+1≥0轉化成函數中的性質，他們就能夠很輕松的解決.具體證明方法如下：設f(a)=ab+bc+ca+1，得到一個關于a的一次函數，因為a、b、c∈[-1，1]，所以f(1)=b+bc+c+1=b(1+c)+(c+1)=(b+1)(c+1)≥0，f(-1)=-b+bc-c+1=-b(1-c)+(1-c)=(1-b)(1-c)≥0，得知f(a)在[-1，1]上恒為負數，則ab+bc+ca+1≥0.

上述案例，處理該題的關鍵點在于學生要具有一定的函數意識，他們通過函數思想的應用構建出一次函數模型，使其根據一次函數的單調性性質展開證明，最終準確解答這一難題.

三、運用函數思想解答數列難題

數列本身就可以看成一類特殊的函數，由于數列內含有具有一定規律的數字，解題時運用函數思想，把每一項都看作函數的量，借助函數思想求出數列的通項公式，由此順利求解.高中生在處理數列類難題時采用函數思想，應當將數列看作一個函數，列出相應的通項公式，結合函數中已知量與未知量之間的關系建立出函數邏輯關系，輔助他們實現求解的目標.

例3已知等差數列{an}的前n項和Sn=m，前m項和Sm=n(m≠n)，求前m+n項的和Sm+n.

解析教師可指導學生利用函數思想來分析等差數列前n項和Sn滿足的關系從函數視角出發，這是一個必過點(0，0)的二次函數，抓住等差數列求和公式是一種特殊的二次函數這函數思想，將m+n看成一個整體，簡化數列的運算量，使其找到突破口.具體解法如下：

設Sn=An2+Bn(n∈N*)，則得到Am2+Bm=n①，An2+Bn=m②，①-②得到A(m2-n2)+B(m-n)=n-m，由于題目指出m≠n，則A(m+n)+B=-1，A(m+n)2+B(m+n)=-(m+n)，所以得到Sm+n=(m+n).

針對上述案例，在解決數列類問題過程中，教師可以引領學生借助函數思想來分析和解答，把復雜的題目變得簡便化，使其通過認真觀察高效、輕松的解題，突破數列難題的困擾.

四、應用函數思想解答幾何難題

函數思想指的是運用函數概念與性質分析、轉變與求解題目，在高中數學知識體系中，解析幾何是也是一大難點，其中求范圍和最值問題不僅常見，還不易解答.這時高中數學教師可以引領學生應用函數思想來思考解析幾何問題，使其從函數性質推理、判斷題目中存在的某些的函數關系，幫助他們確定正確的解題思路，從而有效降低解析幾何題目的難度.

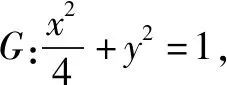
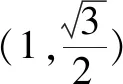
在上述案例中，學生發現本題的命題背景是分式函數，轉化后處理成基本對勾函數或不等式模型，題目由雙變量變成單變量，這是解題的關鍵所在.

五、采用函數思想解題向量難題

平面向量指的是在二維平面內既有方向又有大小的量，與普通的標量相比抽象難懂，而且高中生是初次接觸平面向量，不僅理論知識學習起來難度較大，他們在解題過程中更是困難重重，極易遇到障礙.為幫助學生正確解答平面向量難題，教師可引導他們采用函數思想分析題干內容，理清題目中已知條件與未知條件之間的關系，使其解決難題、求出答案.

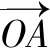
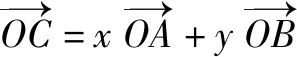
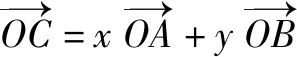
學生使用函數思想這一“代數法”解題，主要考察化歸、轉化及信息遷移能力，解題關鍵在于把向量問題變成三角函數問題，建立出x+y的對應函數式，輕松獲得答案.

總而言之，在高中數學解題教學實踐中，隨著知識難度與深度的提升，題目難度系數也隨之增加，學生遇到難題的概率越來越高，教師需引導他們學會使用函數思想分析與處理題目，使其合理轉化解題思路，找出便捷、高效的解題方法.