基于改進(jìn)飛蛾撲火算法的無(wú)人機(jī)低空突防路徑規(guī)劃
黃 鶴,吳 琨,王會(huì)峰,楊 瀾, 茹 鋒,王 珺
(1. 長(zhǎng)安大學(xué) 電子與控制工程學(xué)院,西安 710064; 2. 長(zhǎng)安大學(xué) 西安市智慧高速公路信息融合與控制重點(diǎn)實(shí)驗(yàn)室,西安 710064; 3. 長(zhǎng)安大學(xué) 信息工程學(xué)院,西安 710064)
無(wú)人機(jī)以低風(fēng)險(xiǎn)、高機(jī)動(dòng)能力等特點(diǎn)被廣泛地應(yīng)用于軍事領(lǐng)域,在執(zhí)行任務(wù)規(guī)劃中,低空突防技術(shù)是無(wú)人機(jī)協(xié)同作戰(zhàn)以及網(wǎng)絡(luò)化作戰(zhàn)的關(guān)鍵技術(shù),合理高效的突防方法可以使無(wú)人機(jī)更有效地躲避威脅區(qū)域,提高任務(wù)執(zhí)行效率及生存幾率,順利完成飛行任務(wù)。
無(wú)人機(jī)突防以有效的規(guī)劃路線(xiàn)方法[1]為基礎(chǔ),其核心取決于尋優(yōu)算法的優(yōu)劣。近年來(lái)國(guó)內(nèi)外學(xué)者在該領(lǐng)域進(jìn)行了大量的研究,提出了諸多有效的突防路徑規(guī)劃算法,如最速下降法[2]、Voronoi 圖法[3]、遺傳算法[4]、A*智能算法[5]等。目前最新、使用最廣泛的方法是采用群體智能優(yōu)化算法求解無(wú)人機(jī)突防路徑的問(wèn)題。唐立等提出了一種基于改進(jìn)的蟻群算法的路徑規(guī)劃方法[6],通過(guò)構(gòu)造泰勒多邊形構(gòu)造路徑可行解并建立路徑安全度約束,縮小搜索范圍,再通過(guò)蟻群算法尋找最優(yōu)路線(xiàn)。該方法提升了尋優(yōu)效率,但路徑的精確度不高。宋宇等提出了一種基于三維規(guī)劃的改進(jìn)粒子群優(yōu)化方法[7],提升了全局及局部搜索性能,但由于將威脅場(chǎng)考慮的比較簡(jiǎn)單,并未考慮地形等因素,因此實(shí)際應(yīng)用效果并不理想。近年來(lái),許江波等通過(guò)自適應(yīng)策略改進(jìn)魚(yú)群算法,利用其全局尋優(yōu)能力解決路徑規(guī)劃問(wèn)題[8],但該算法的不足還是搜索時(shí)間過(guò)長(zhǎng)。
同時(shí),在三維無(wú)人機(jī)路徑規(guī)劃過(guò)程中,由于地形與威脅源的信息量大,使群體智能優(yōu)化算法尋求最優(yōu)路徑時(shí)復(fù)雜度呈現(xiàn)指數(shù)上漲,極易陷入局部最優(yōu)。而飛蛾撲火算法因其獨(dú)特的尋優(yōu)方式及更新策略可以在復(fù)雜度較高的情況下具備良好的尋優(yōu)能力。因此,本文提出一種基于改進(jìn)飛蛾撲火算法的三維無(wú)人機(jī)低空突防方法,在保證高精確度的情況下,盡量縮短尋優(yōu)時(shí)間,快速有效地獲得無(wú)人機(jī)突防的最優(yōu)路徑。
1 無(wú)人機(jī)三維突防環(huán)境建模
在處理靜態(tài)三維環(huán)境的無(wú)人機(jī)突防問(wèn)題時(shí),最重要的是根據(jù)任務(wù)、威脅情況,以及地形等已知因素構(gòu)建三維的地形和威脅環(huán)境約束。本文將基本地形、雷達(dá)監(jiān)測(cè)、火炮威脅、無(wú)人機(jī)物理約束等進(jìn)行數(shù)學(xué)建模,并通過(guò)數(shù)字融合,構(gòu)建出三維環(huán)境下的地形約束。
1.1 地形約束
不同任務(wù)中,無(wú)人機(jī)面臨的實(shí)際戰(zhàn)場(chǎng)環(huán)境是不相同的,根據(jù)海拔不同,將地形分為平原地區(qū),山地地區(qū),丘陵地區(qū)三種地形,其中影響最大因素的是山峰,同時(shí)也要考慮海拔變化帶來(lái)的影響。首先,三維環(huán)境下的山峰建模如下所示:
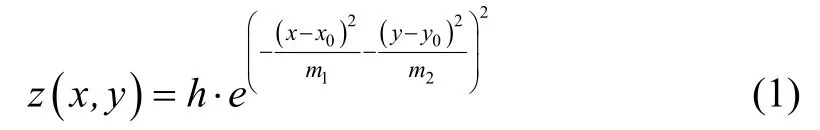
其中,(x,y)為山峰地形在水平平面上對(duì)應(yīng)的坐標(biāo),(x0,y0)為山峰地形在水平平面上的中心點(diǎn)坐標(biāo),h為高度參數(shù),m1和m2反應(yīng)山峰的陡峭程度。另外,航跡點(diǎn)的地形威脅代價(jià)如下:
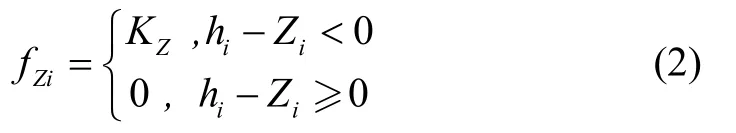
其中:Kz為地形威脅系數(shù),hi為第i個(gè)航跡點(diǎn)的海拔高度,Hi為第i個(gè)航跡點(diǎn)距離地形的垂直高度,fzi為第i個(gè)航跡點(diǎn)對(duì)應(yīng)的威脅代價(jià)。此外,無(wú)人機(jī)低空突防需考慮高程代價(jià),航跡點(diǎn)的高程代價(jià)如式(3)所示:

無(wú)人機(jī)在突防中的地形約束還需要考慮到飛行邊界范圍以及最大飛行高度,保證操控?zé)o人機(jī)的安全性。因此設(shè)定無(wú)人機(jī)飛行水平范圍為(Xmin,Ymin)和(Xmax,Ymax),最大飛行高度為Hmax。
1.2 威脅模型約束
雷達(dá)、電磁威脅、導(dǎo)彈是無(wú)人機(jī)突防的主要威脅來(lái)源,具體建模如下:
(1) 雷達(dá)威脅
雷達(dá)主要通過(guò)電磁波來(lái)探測(cè)目標(biāo)的距離,速度,相對(duì)位置等敵方信息,顯然,要使無(wú)人機(jī)順利突防,必須在飛行過(guò)程中避開(kāi)雷達(dá)的探測(cè)范圍,保證安全。
描述雷達(dá)方程特性的方程如下:
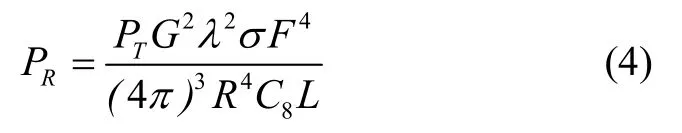
其中,主要因素是P,也就是目標(biāo)和雷達(dá)之間的距離,因此雷達(dá)方程簡(jiǎn)化為雷達(dá)探測(cè)概率模型如下:
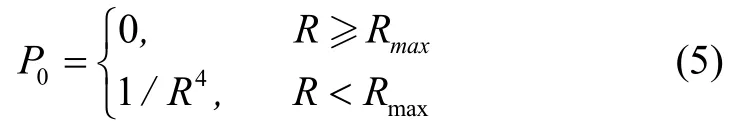
(2) 電磁威脅
一般情況下,電磁威脅可視作半球型,威脅模型如下:
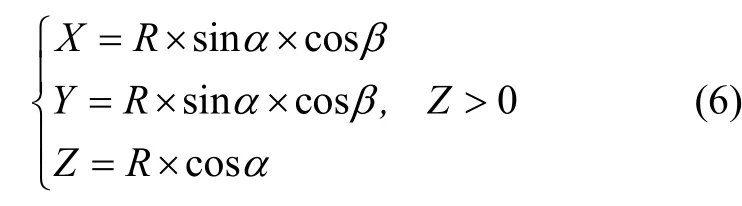
其中,R為電磁干擾的半徑,α為Z 軸正向與半徑的夾角,β為半徑在水平面上的投影與X 軸正向的夾角。
(3) 導(dǎo)彈威脅
敵方導(dǎo)彈的威脅范圍內(nèi)也被稱(chēng)作禁飛區(qū),必須躲避。在三維平面上,導(dǎo)彈威脅范圍近似于一個(gè)半球體。 無(wú)人機(jī)在禁飛區(qū)半徑內(nèi)下被擊中的可能性為:
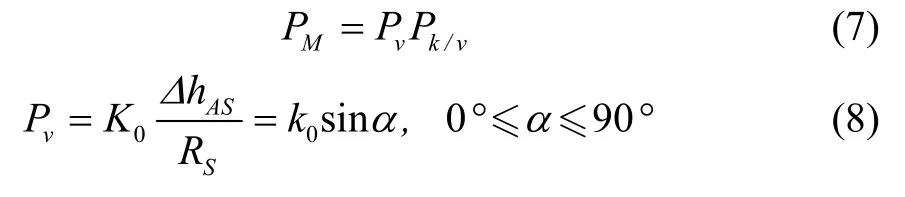
其中,Pk/v為常數(shù),表示無(wú)人機(jī)在禁飛區(qū)半徑內(nèi)被摧毀的概率;K0為比例系數(shù),Rs為導(dǎo)彈威脅中心與無(wú)人機(jī)之間的斜距;α為視線(xiàn)俯視角。則:
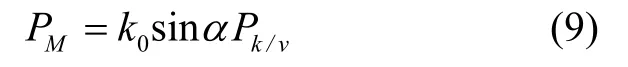
在三維建模過(guò)程中,威脅源半徑較大,而無(wú)人機(jī)限高較低,因此可以將威脅源等效為圓柱地形處理[9]。航跡的威脅代價(jià)如下:

其中,KTj為威脅源j的威脅系數(shù),rij為第i個(gè)航跡點(diǎn)到威脅源j中心的直線(xiàn)距離,RTj為威脅源j的威脅半徑,F(xiàn)T,ij為第i個(gè)航跡點(diǎn)到威脅源j中心的代價(jià)。
1.3 無(wú)人機(jī)約束
無(wú)人機(jī)在飛行過(guò)程中受自身的物理約束,主要有最大轉(zhuǎn)彎角α、最大下滑及爬升角β,以及燃油代價(jià),中燃油代價(jià)用路程表示。各物理約束分別為:
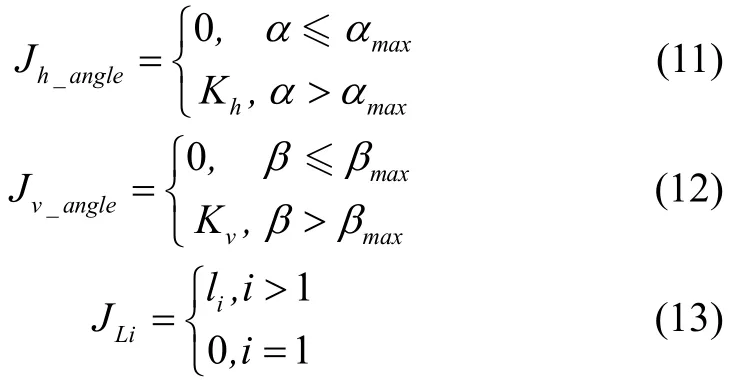
式中,Kh和Kv分別為轉(zhuǎn)彎角和俯仰角威脅系數(shù),Jh_angle,i和Jv_angle,i分別為第i個(gè)航跡點(diǎn)對(duì)應(yīng)的α和β的代價(jià)函數(shù)。綜合各代價(jià)函數(shù),可得出第i個(gè)航跡點(diǎn)的無(wú)人機(jī)物理約束代價(jià)函數(shù)為:
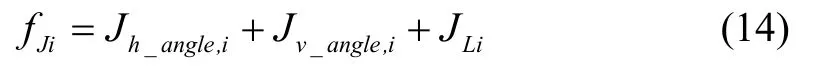
1.4 航跡代價(jià)函數(shù)
將地形約束、高程代價(jià)、威脅模型約束及無(wú)人機(jī)自身物理約束的代價(jià)加權(quán)綜合起來(lái)就構(gòu)成最終的無(wú)人機(jī)代價(jià)函數(shù),如式(15)所示。
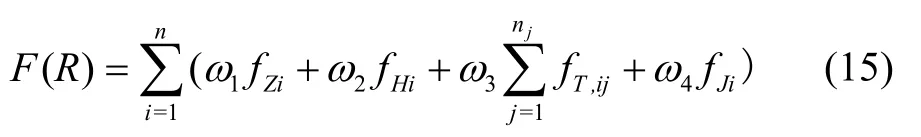
式中,F(xiàn)(R)為整條航跡的代價(jià),ω1,ω2,ω3,ω4為各代價(jià)的權(quán)重。
2 改進(jìn)的飛蛾撲火算法
2.1 飛蛾撲火算法
飛蛾撲火算法(Moth-flame Optimization, MFO)是受到飛蛾圍繞火焰對(duì)數(shù)螺旋線(xiàn)形式運(yùn)動(dòng)的現(xiàn)象啟發(fā)而提出的一種新型的元啟發(fā)算法[10]。在算法中,飛蛾為待優(yōu)化的問(wèn)題,火焰為每次迭代的最優(yōu)解,通過(guò)螺旋更新改變飛蛾自身的位置以及火焰的結(jié)構(gòu)。
2.1.1 飛蛾種群的初始化
定義飛蛾的特征有d維,設(shè)初始飛蛾個(gè)數(shù)為n,路徑點(diǎn)的個(gè)數(shù)為d,則飛蛾種群M如式(16)所示。
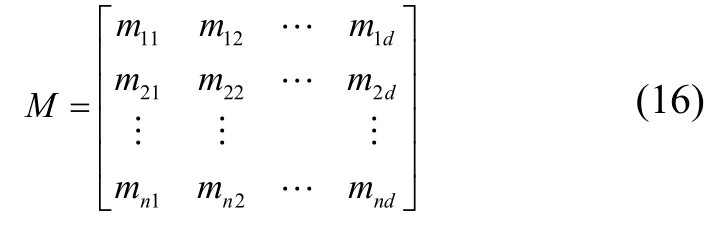
其中,定義Mi為飛蛾種群M中的第i只飛蛾。飛蛾適應(yīng)度的大小由OM表示:

其中,Omi為第i只飛蛾的適應(yīng)度,通過(guò)相應(yīng)的代價(jià)函數(shù)得到。初始火焰的集合與M大小一致,并隨著后續(xù)的迭代,火焰的數(shù)量會(huì)逐漸減小,火焰集合由F表示。
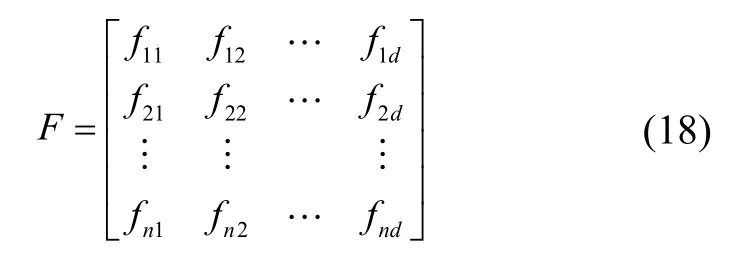
其中,第i個(gè)火焰由Fi表示。火焰的適應(yīng)度值OF的大小同樣為n×1,如式(19)所示。
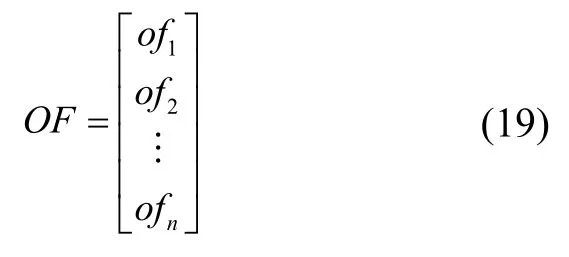
其中,ofi表示第i(i=1,2,…,n)個(gè)火焰的適應(yīng)度值。OF矩陣是OM中每個(gè)向量排序之后的結(jié)果,所以F是M矩陣根據(jù)OF矩陣的排序得到的結(jié)果,這說(shuō)明火焰F是飛蛾M在當(dāng)前迭代搜索中的最優(yōu)解。
2.1.2 迭代更新
MFO 算法每輪的更新機(jī)制可分為兩個(gè)階段:飛蛾撲火、飛蛾棄焰。
(1)飛蛾撲火:根據(jù)飛蛾的趨光性,飛蛾Mi圍繞對(duì)應(yīng)的火焰Fj做對(duì)數(shù)螺旋曲線(xiàn)運(yùn)動(dòng)。定義對(duì)數(shù)螺旋曲線(xiàn)如式(20)所示:
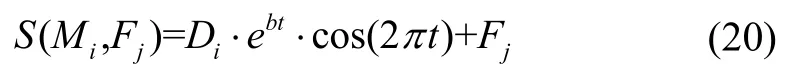
其中,S(Mi,Fj)是飛蛾更新后的新位置,Di是第j個(gè)火焰與第i只飛蛾的歐式距離,b為常數(shù)參數(shù),可調(diào)整對(duì)數(shù)螺旋曲線(xiàn),通常取1。參數(shù)t為[-1,1]范圍內(nèi)的一個(gè)隨機(jī)數(shù),表示當(dāng)前飛蛾的更新位置與火焰的接近度,則t=-1 代表飛蛾與火焰最近,t=1 則兩者相距最遠(yuǎn)。具體過(guò)程如圖1 所示。
(2)飛蛾棄焰:為了提高算法的收斂速度并保證飛蛾種群向最優(yōu)靠近,應(yīng)逐漸減少較差的火焰,飛蛾僅圍繞保留下來(lái)的火焰做旋轉(zhuǎn)運(yùn)動(dòng),從而避免飛蛾丟失最優(yōu)解的情況。火焰自適應(yīng)減少如公式(21)所示:
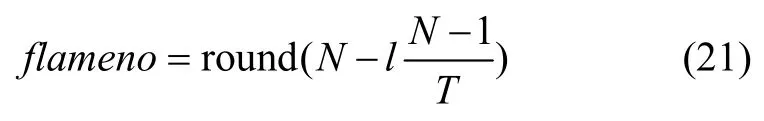
其中,flameno為當(dāng)前火焰數(shù)量,N為種群數(shù),l為當(dāng)前的迭代次數(shù),T為規(guī)定的最大迭代次數(shù)。
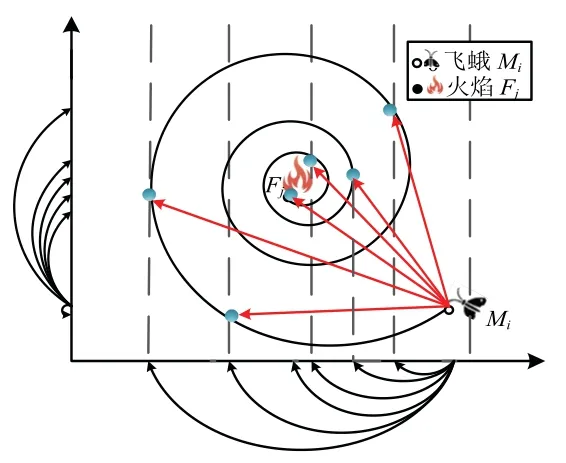
圖1 飛蛾運(yùn)動(dòng)軌跡圖Fig.1 Moth tracks
2.2 基于改進(jìn)的MFO 算法的無(wú)人機(jī)三維路徑規(guī)劃
2.2.1 航跡編碼
在實(shí)際應(yīng)用中,每條路徑都是由多個(gè)航跡點(diǎn)連接而成的線(xiàn)。定義種群中的一只飛蛾Mi即為一條路徑,Mi=[mi1,mi2,……,min],每個(gè)航跡點(diǎn)mi1具有空間三維的屬性(x,y,z)。同時(shí),在利用MFO 算法規(guī)劃三維的無(wú)人機(jī)突防路徑的問(wèn)題時(shí),首先確定航跡點(diǎn)數(shù)n,其次等距離x方向的航跡點(diǎn)坐標(biāo)固定不變,通過(guò)對(duì)y和z坐標(biāo)的尋優(yōu)確定最優(yōu)突防路線(xiàn)。
2.2.2 自適應(yīng)慣性權(quán)重
慣性權(quán)重在平衡算法的全局及局部搜索能力中起著至關(guān)重要的作用。傳統(tǒng)MFO 算法中的火焰并未能被充分利用,因此,本文在飛蛾的更新策略上引入了自適應(yīng)權(quán)重。通常,在群體智能算法中自適應(yīng)權(quán)重加在步長(zhǎng)上,而本文改變其更新機(jī)制,通過(guò)將自適應(yīng)權(quán)重放在火焰上擾動(dòng)火焰的位置保證充分發(fā)揮最優(yōu)解的優(yōu)勢(shì)。自適應(yīng)權(quán)重ρ如下表示:
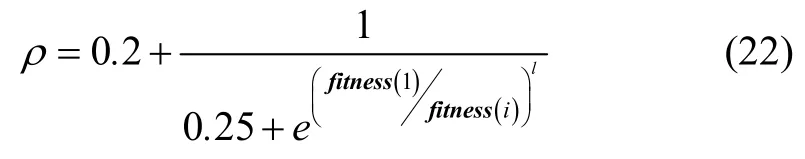
其中,fitness(i)為當(dāng)前迭代中第i只飛蛾的適應(yīng)度,l為當(dāng)前迭代次數(shù),當(dāng)l逐漸增大時(shí),自適應(yīng)權(quán)重ρ趨向于1。引入權(quán)值后的位置更新策略如下:
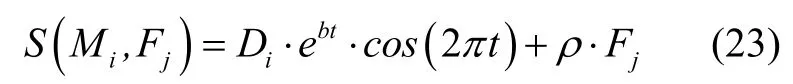
將自適應(yīng)慣性權(quán)重策略引入進(jìn)MFO 的位置更新機(jī)制中,在算法前期,使得不易于快速收斂到局部最優(yōu)解,在迭代過(guò)程中跳出局部最優(yōu)尋求全局最優(yōu)。在尋優(yōu)后期,權(quán)重趨向于1,保證局部最優(yōu)解的精確度。
2.2.3 改進(jìn)的交叉算子與變異算子
遺傳算法在求解多峰函數(shù)及復(fù)雜問(wèn)題時(shí)的高效性非常適合與MFO 相結(jié)合[11-13]。遺傳算子主要包括三個(gè)方面:交叉算子、變異算子、遺傳算子。針對(duì)MFO因自身尋優(yōu)方法存在早熟性,在求解三維環(huán)境下最優(yōu)路徑時(shí)無(wú)法快速定位到最優(yōu)路徑等問(wèn)題,本文將火焰矩陣與遺傳算法的交叉算子、變異算子相結(jié)合并加以改進(jìn),使算法在前期快速跳出局部最優(yōu),增強(qiáng)算法的收斂性能。主要思想是每次迭代時(shí)將最優(yōu)火焰與其余隨機(jī)火焰進(jìn)行交叉重組,并與原來(lái)父代的適應(yīng)度作對(duì)比,若相對(duì)原來(lái)父代適應(yīng)度較優(yōu),則替換父代。交叉算子表示如下:
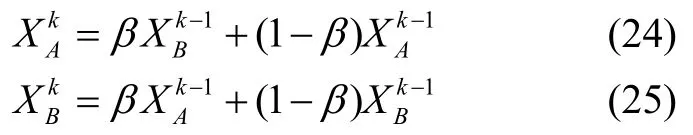
其中,XAk代表第k代火焰矩陣中的最優(yōu)火焰?zhèn)€體,XBk表示此外的任一隨機(jī)火焰?zhèn)€體,β為一系數(shù),當(dāng)β為常數(shù)時(shí),稱(chēng)為均勻交叉算子,當(dāng)β隨迭代次數(shù)改變時(shí),則稱(chēng)為非均勻交叉算子。
新一代的火焰?zhèn)€體主要由系數(shù)β及上一代的個(gè)體來(lái)共同決定,當(dāng)β趨近于0.5 時(shí),子代遠(yuǎn)離父代,可以拓寬搜索空間,保證火焰種群具有多樣性,當(dāng)β遠(yuǎn)離0.5 時(shí),子代靠近父代,保證搜索范圍縮小,使得精確度提高。因此,在交叉算子的基礎(chǔ)上做如下做改進(jìn):
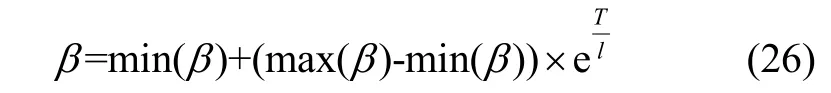
其中,min(β)及max(β)分別代表β的最大值及最小值。β系數(shù)曲線(xiàn)如圖2 所示.
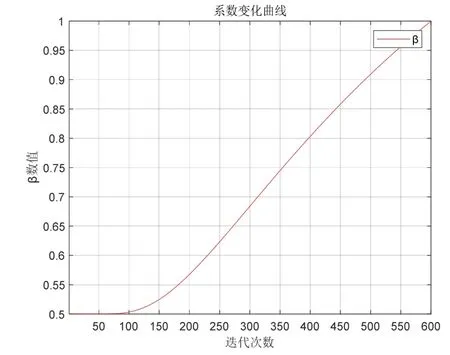
圖2β 系數(shù)變化曲線(xiàn)圖Fig.2 Curve of β coefficient change
由圖2 可知,為了保證在迭代初期XA及XB在后代中有較為平均的基因占比,以及火焰矩陣的多樣性,取β的初始值為0.5,并使其在前期增長(zhǎng)緩慢。隨迭代次數(shù)的增長(zhǎng)β迅速靠近1,使種群多樣性降低,搜索精度增加。
呂曉英(以下簡(jiǎn)稱(chēng)呂):我的審美觀念,或者說(shuō)欣賞趣味,可能是屬于比較傳統(tǒng)的。我以為,小說(shuō)、電影的中心應(yīng)該是故事,音樂(lè)、歌曲的中心是旋律,我喜歡有故事性和旋律性的作品。而當(dāng)今的許多作品卻似乎背離了這種傳統(tǒng)特征,小說(shuō)、電影越來(lái)越不會(huì)講述一個(gè)故事,音樂(lè)、歌曲也越來(lái)越不會(huì)演繹一段旋律。可能就因此,我和許多小說(shuō)的潛在讀者一樣,逐漸放棄小說(shuō),喜歡看電視劇勝過(guò)看電影,因?yàn)樵陔娨晞∵@種文化形態(tài)中,故事性被表現(xiàn)得最為充分。
(2)高斯變異算子
由于地形比較復(fù)雜,在MFO 尋優(yōu)過(guò)程中,個(gè)別航跡點(diǎn)迭代時(shí)無(wú)法跳出局部最優(yōu),使航跡出現(xiàn)較大偏差,需加入高斯變異算子對(duì)航跡點(diǎn)隨機(jī)干擾。設(shè)其中一個(gè)火焰為Fi=[f1f2...fd],每一維度根據(jù)變異率p選擇是否產(chǎn)生變異。假設(shè)第k維產(chǎn)生變異,則高斯變異算子為

其中,fk為火焰第k維的特征,f'k為變異后的特征,λ為系數(shù),受空間大小影響,決定變異的程度大小。
2.3 三次樣條插值平滑路徑算法
在無(wú)人機(jī)實(shí)際飛行中,為了保證無(wú)航跡轉(zhuǎn)彎角平滑,避免無(wú)人機(jī)受到自身物理約束及性能的限制,采用三次樣條改善最終突防路徑。設(shè)最終無(wú)人機(jī)突防路徑為:Z=(z1,z2……zn),每個(gè)路徑點(diǎn)zk(k=1……n)有(x,y,z)三個(gè)維度,分別對(duì)(x1,x2……xn)、(y1,y2……yn)、(z1,z2……zn)做三次樣條插值,最終形成一條光滑路徑,三次樣條插值效果如圖3 所示。
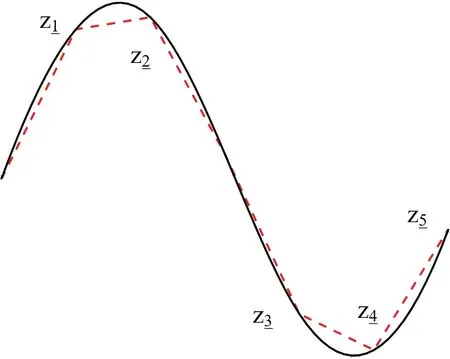
圖3 三次樣條插值優(yōu)化效果圖Fig.3 Cubic spline interpolation optimization effect diagram
總的算法流程如表1 和圖4 所示。

表1 本文算法流程Tab.1 Algorithm flow of this paper
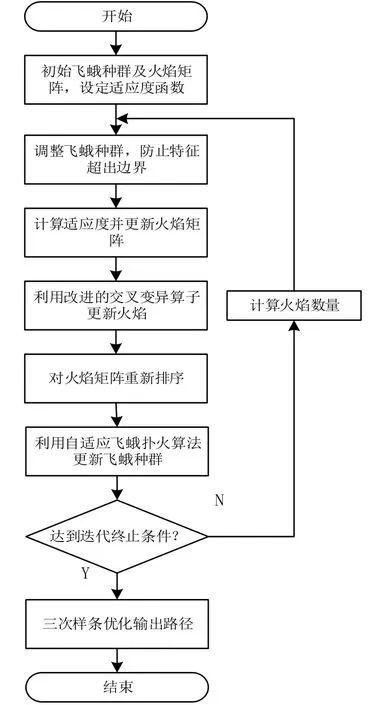
圖4 本文算法流程圖Fig.4 The flow chart of this algorithm
3 改進(jìn)的飛蛾撲火算法對(duì)比實(shí)驗(yàn)
3.1 測(cè)試函數(shù)
由于無(wú)人機(jī)面對(duì)復(fù)雜地形突防時(shí),多極值的尋優(yōu)性能非常關(guān)鍵。選擇使用基準(zhǔn)測(cè)試函數(shù)中兩個(gè)單峰函數(shù)Quartic 和Sum Squares 及兩個(gè)多峰函數(shù)Penalized1和Penalized2 來(lái)評(píng)估算法性能,它們能在復(fù)雜度較高的情況下驗(yàn)證算法能否跳出局部最優(yōu)。測(cè)試函數(shù)描述如下:
(1) Quartic 函數(shù)
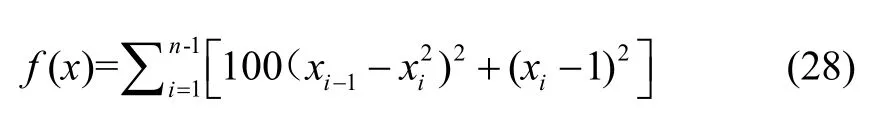
(2) Sum Squares 函數(shù)
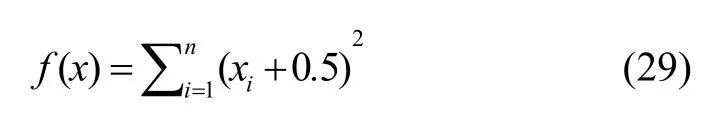
其中,xi∈[-100,100],n=10, 全局最小值處為(0,0…0)。
(3) Penalized 1 函數(shù)
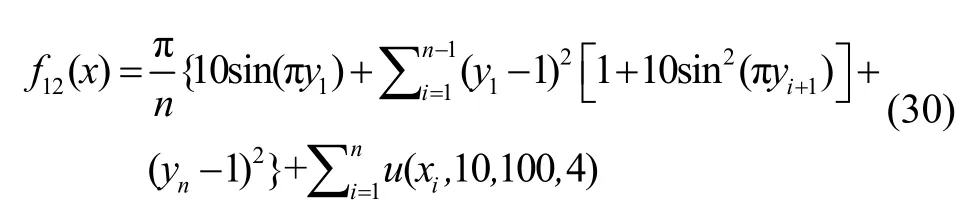
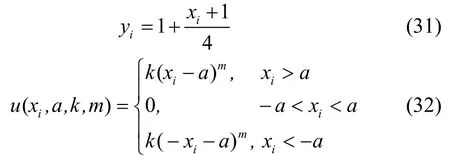
其中,xi∈[-30, 30],n=10,全局最小值處為(0,0…0)。
(4) Penalized 2 函數(shù)
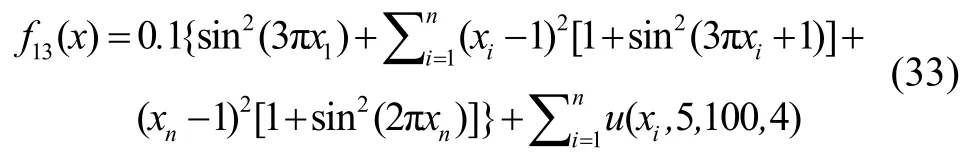
其中,xi∈[-30,30],n=10, 全局最小值處為(0,0…0)。
3.2 實(shí)驗(yàn)驗(yàn)證
采用上述4 種測(cè)試函數(shù)分別評(píng)估MFO 算法、灰狼算法(Grey Wolf Optimizer, GWO)算法[14]以及本文算法的尋優(yōu)性能。圖5 為各算法在不同測(cè)試函數(shù)上的適應(yīng)度曲線(xiàn)圖,表2 列出了各算法經(jīng)過(guò)測(cè)試函數(shù)20次測(cè)試的均值及最優(yōu)值。

由圖5 可知,GWO 在Quartic 函數(shù)上的尋優(yōu)性能相比于MFO 較好,在其余測(cè)試函數(shù)上收斂速度及精度均不如MFO,而本文算法在各測(cè)試函數(shù)上收斂速度及精度均優(yōu)于其余兩種算法,說(shuō)明本文算法在復(fù)雜度較高的測(cè)試函數(shù)上有較強(qiáng)的尋優(yōu)能力。由表2 可知,MFO 在Quartic 函數(shù)上表現(xiàn)較差,其余測(cè)試函數(shù)上最優(yōu)值雖較好,但均值與最優(yōu)值相差較大,波動(dòng)明顯。GWO 在多峰測(cè)試函數(shù)上精度較低,但較為穩(wěn)定。而本文算法在各多峰函數(shù)上精度相比于MFO 及GWO均有較大提升,并且尋優(yōu)穩(wěn)定。這說(shuō)明,本文提出的改進(jìn)方法可以有效幫助MFO 算法跳出局部最優(yōu)解,增強(qiáng)了MFO 算法面對(duì)復(fù)雜問(wèn)題時(shí)的全局尋優(yōu)能力。
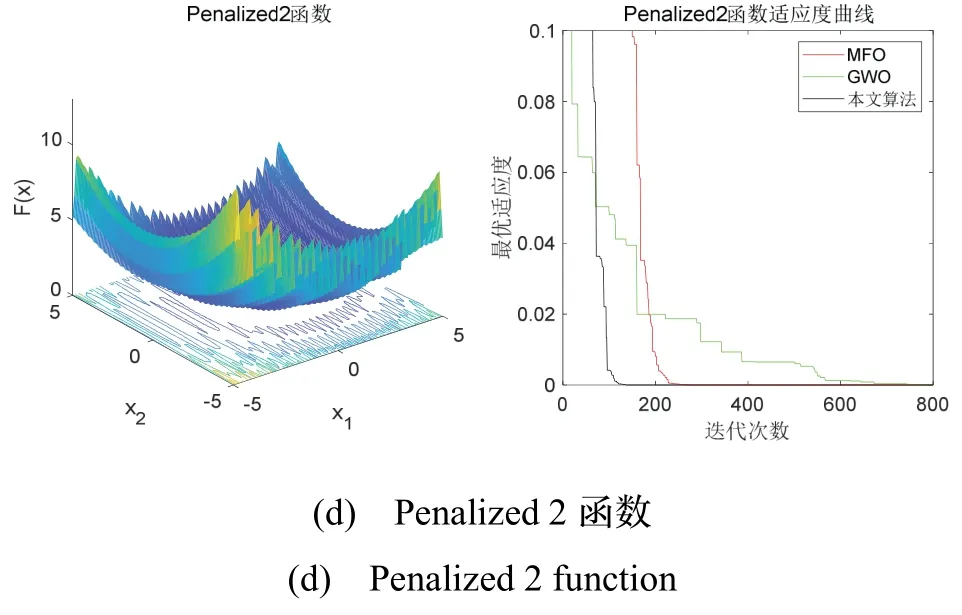
圖5 各算法在測(cè)試函數(shù)上的適應(yīng)度曲線(xiàn)圖Fig.5 The fitness curve of each algorithm on test function
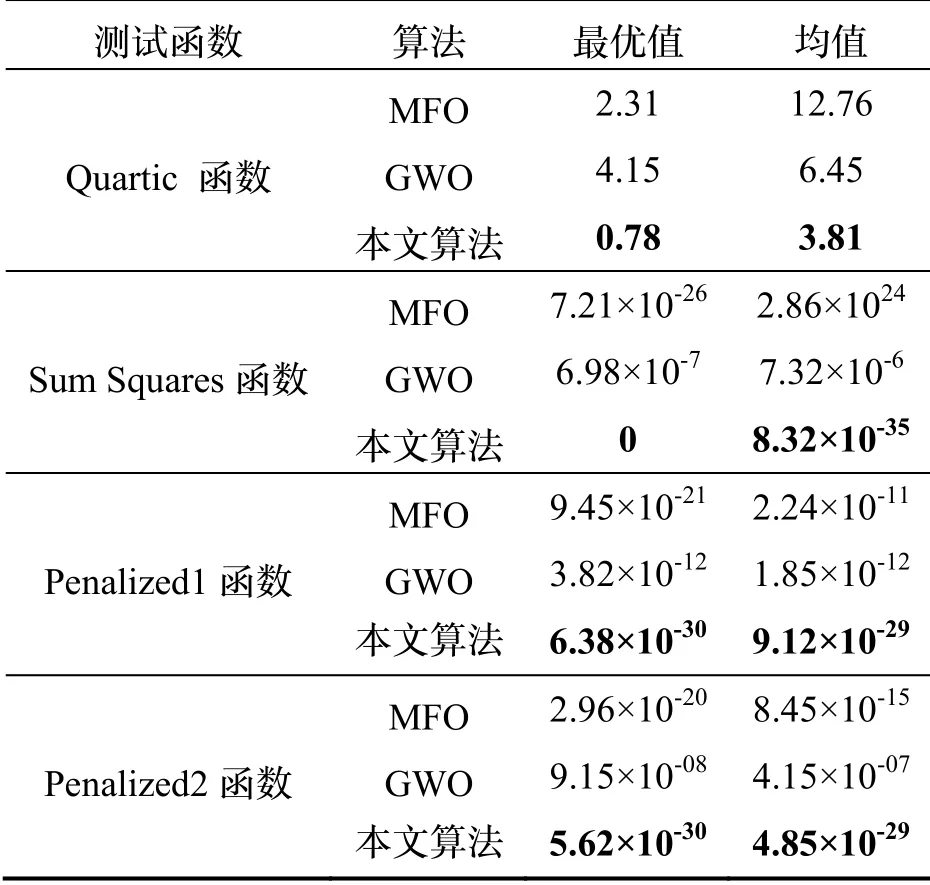
表2 三種算法在測(cè)試函數(shù)上的實(shí)驗(yàn)對(duì)比Tab.2 Experimental comparison of three algorithms on test functions
4 無(wú)人機(jī)突防仿真測(cè)試及分析
仿真測(cè)試計(jì)算機(jī)的CPU 為Intel Core i7-9750U CPU 2.60GHz、內(nèi)存為16GB,操作系統(tǒng)為Windows10,編譯軟件為Matlab R2018a。測(cè)試地形區(qū)域大小為100 km×100 km,測(cè)試限高為4 km。無(wú)人機(jī)航線(xiàn)的起始點(diǎn)與終止目標(biāo)分別為(1, 3, 0.5)及(99, 98, 0.5),敵方雷達(dá)及火炮距離的中心為(20, 13.5, 0)、(85, 60, 0)、(40, 59, 0),作用半徑為9 km。MFO、GWO 和本文算法求得三條路徑的航跡點(diǎn)分別用圓圈、星號(hào)、及正方形表示。各算法種群數(shù)設(shè)為100,最大迭代次數(shù)為800 次。算法參數(shù)以及無(wú)人機(jī)突防軌跡圖分別如表3和圖6 所示。
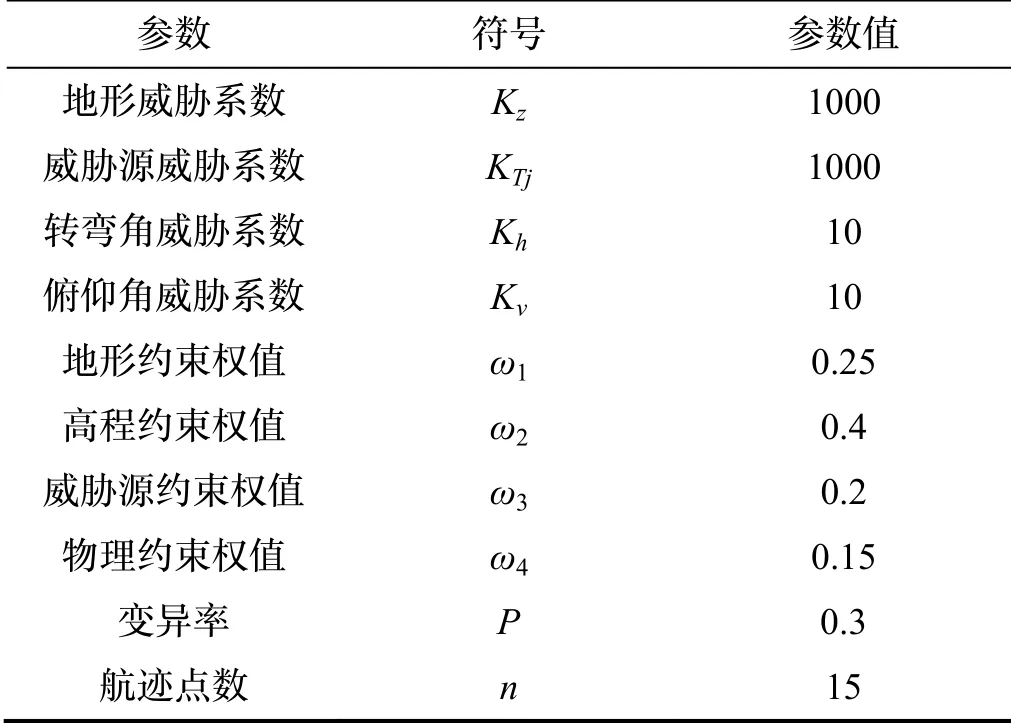
表3 主要參數(shù)Tab.3 Main parameters
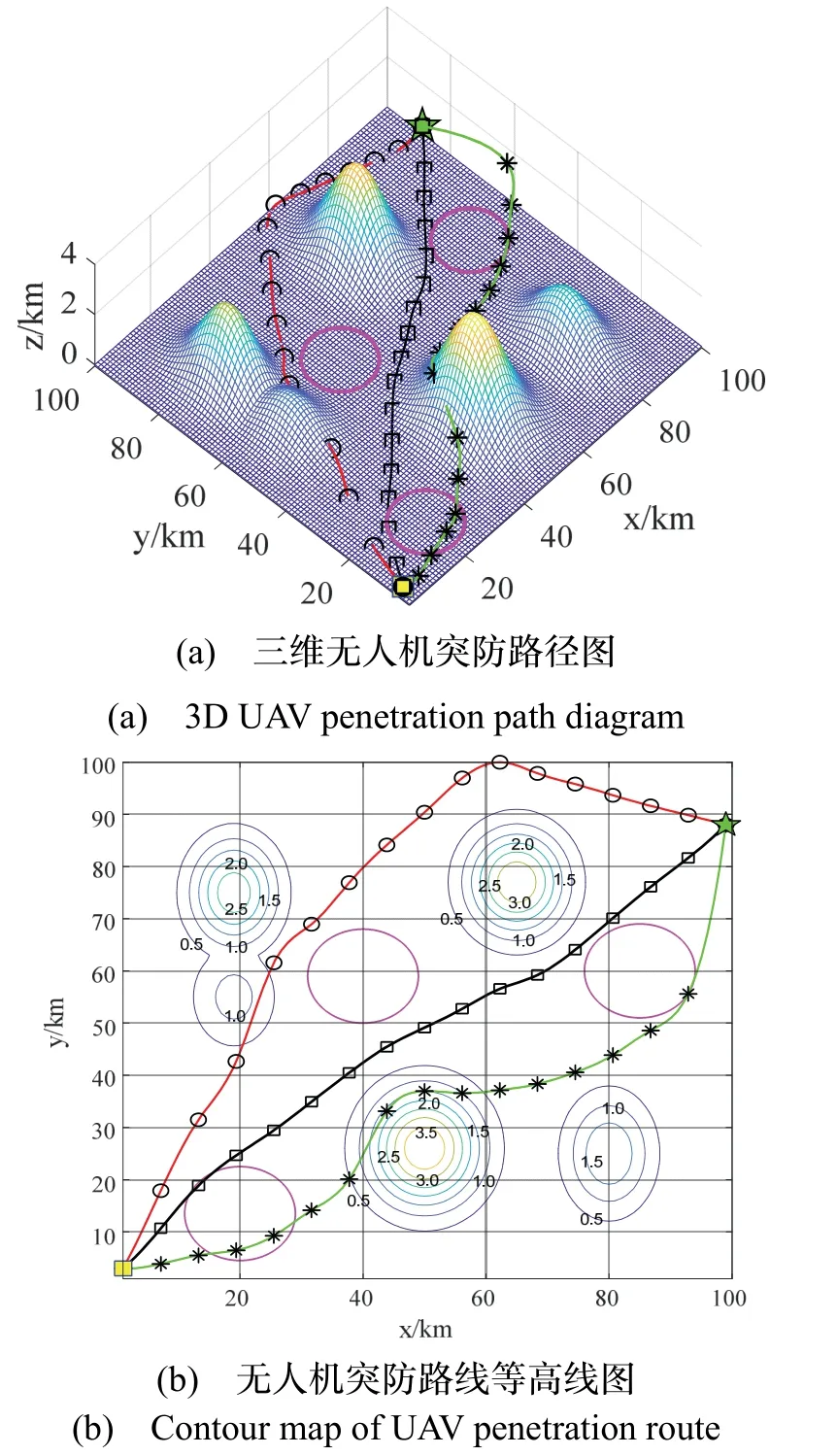
圖6 無(wú)人機(jī)突防路線(xiàn)軌跡圖Fig.6 Path map of UAV penetration route
通過(guò)MFO、GWO、本文算法在無(wú)人機(jī)突防路線(xiàn)軌跡圖中的對(duì)比可以看出,傳統(tǒng)MFO 規(guī)避了威脅源,但路徑中有部分穿過(guò)了地形,規(guī)劃的路線(xiàn)較長(zhǎng);GWO的規(guī)劃路線(xiàn)普遍飛行高度高,穿過(guò)了第一個(gè)威脅源,對(duì)無(wú)人機(jī)自身的物理約束沒(méi)有滿(mǎn)足,俯仰角過(guò)大;而本文算法可以有效地利用地形優(yōu)勢(shì),在規(guī)避山峰地形及各威脅源的同時(shí),滿(mǎn)足無(wú)人機(jī)自身的物理約束,并做到貼地飛行,避免路徑中出現(xiàn)多余路線(xiàn),從而達(dá)到低空突防的目的。算法的航程和最優(yōu)代價(jià)如表4 所示,最優(yōu)航線(xiàn)代價(jià)變化如圖5 所示。
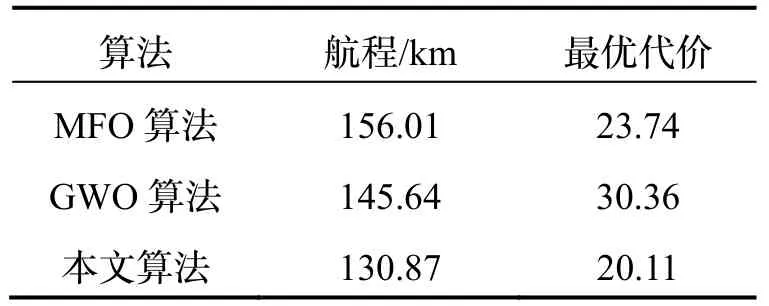
表4 算法航程及最優(yōu)代價(jià)Tab.4 Algorithm voyage and optimal cost
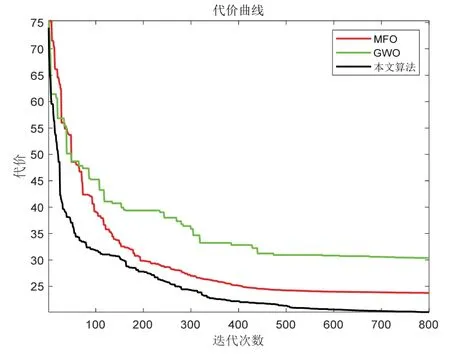
圖7 最優(yōu)路線(xiàn)代價(jià)變化圖Fig.7 Optimal route cost change graph
仿真結(jié)果表明,MFO 在尋優(yōu)前期可以跳出局部最優(yōu),但收斂速度相對(duì)較慢,在迭代到400 次左右陷入局部最優(yōu),求得的突防路徑最長(zhǎng);GWO 在復(fù)雜度較高的情況下效果較差,尋優(yōu)過(guò)程中難以跳出局部極值,且精度較低,難以適應(yīng)三維地形下無(wú)人機(jī)突防路徑規(guī)劃;而本文算法無(wú)論在精度、速度方面,都優(yōu)于MFO及GWO,最短路徑比MFO 及GWO 算法分別降低了25.14 km 和14.77 km,求得路徑最短,代價(jià)分別降低了3.63 及10.25。通過(guò)算法比較,本文算法可以更為有效地避開(kāi)威脅地形及威脅源,利用地形作掩護(hù)實(shí)現(xiàn)低空突防。
5 結(jié) 論
本文針對(duì)無(wú)人機(jī)的低空突防路徑規(guī)劃問(wèn)題,提出了一種基于改進(jìn)MFO 的三維無(wú)人機(jī)低空突防方法。首先,建立三維地形模型、威脅源模型及無(wú)人機(jī)物理約束模型,確定威脅代價(jià)函數(shù)。其次,針對(duì)MFO 算法易發(fā)生早熟收斂,收斂速度慢,陷入局部最優(yōu)等問(wèn)題,提出了兩種改進(jìn)思路:(1)利用自適應(yīng)權(quán)重改變MFO 的更新軌跡,加快算法的收斂速度并改善局部搜索性能;(2)在MFO 中引入交叉算子和變異算子,擴(kuò)大搜索空間,進(jìn)一步提升了算法精度,有效解決了MFO 自身缺陷。最后,利用三次樣條插值改善突防路徑,最大程度避免無(wú)人機(jī)受到自身物理約束的限制。實(shí)驗(yàn)表明,該方法可以更精確、快速地使無(wú)人機(jī)自主避開(kāi)危險(xiǎn)區(qū)域選擇最優(yōu)路徑,實(shí)現(xiàn)低空突防。
 中國(guó)慣性技術(shù)學(xué)報(bào)2021年2期
中國(guó)慣性技術(shù)學(xué)報(bào)2021年2期
- 中國(guó)慣性技術(shù)學(xué)報(bào)的其它文章
- 旋轉(zhuǎn)導(dǎo)向鉆井工具姿態(tài)測(cè)量陀螺儀故障估計(jì)與處理方法
- 基于等效樣本和實(shí)仿融合的現(xiàn)場(chǎng)小子樣試驗(yàn)制導(dǎo)精度評(píng)估方法
- 基于人體上肢運(yùn)動(dòng)信息的助殘手抓取意圖識(shí)別方法
- 空芯微結(jié)構(gòu)光纖陀螺性能提升分析與驗(yàn)證
- A method of heating a spinning metal sphere in an elliptical rotating magnetic field with null-torque
- 基于激光干涉的微重力加速度測(cè)量方法
