暖機對航空發動機性能模型的影響分析
錢仁軍,宋漢強,李本威,朱飛翔,張 赟
(1.海軍航空大學,山東 煙臺 264001; 2.海軍研究院,上海 200436)
1 引言
渦扇發動機在啟動成功后,按照規定需先進行暖機操作,即將高壓轉子轉速保持在一定轉速,并維持一段時間,再將發動機由慢車運行到最大狀態。對應飛機的起飛流程,即在起飛前,需先將飛機運行到暖機位進行暖機,然后行駛到起飛位準備起飛。暖機的存在影響了飛機出動程序和出動路線的規劃,嚴重制約了飛機的出動效率,已經成為提高飛機出動效率的瓶頸問題。
已有研究表明,發動機不暖機直接運行到最大狀態,相比暖機后葉尖間隙有所增大[1]。而發動機性能與葉尖間隙密切相關,葉尖間隙的變化會直接影響到部件的效率和流量,并進一步影響整機性能和油耗[2]。臺架數據也表明,發動機不暖機直接運行到最大狀態與暖機后的最大狀態在性能上存在差異。
航空發動機具有制造成本高和試驗費用高的特點[3],直接在發動機本體上進行暖機對整機性能的影響試驗,不僅試驗費用非常昂貴,同時由于暖機對發動機結構的影響還可能導致對發動機造成額外損傷。發動機性能模型仿真技術已經成為避免以上問題的有效手段[4]。利用發動機性能模型替代真實發動機進行仿真研究,可以獲得不同環境參數和不同狀態下發動機的總體性能,以及一些臺架試車無法測量的參數。
發動機模型建模方法主要有解析法和試驗測定法[5]。解析法又稱為部件法,是利用部件特性數據通過氣動熱力學和共同工作方程建立的模型[6]。試驗測定法是利用不同條件下發動機測得的試驗數據,通過系統辨識方法建立模型,因此試驗測定法建立的模型又稱為辨識模型[7-8]。相比部件級模型,辨識模型對試驗數據要求更高,其試驗成本和試驗難度也都高于部件級模型。
考慮到不暖機直接將發動機運行到最大狀態可能對發動機造成的損傷,無法對發動機進行長時間或者不同環境下的多次不暖機試車,無法獲得足夠的不暖機試驗數據,因此,無法通過建立辨識模型對發動機輸入條件進行泛化。故本文采用部件法建立發動機的性能模型。
發動機部件級建模方法最早是由NASA Lewis研究中心提出[9-10],并在90年代結合面向對象的設計思想,進一步推出了推進系統數值仿真計劃(NPSS)[11]。國內在20世紀90年代后陸續開始采用變比熱法進行部件級建模,其建模方法至今在新型發動機建模領域仍有廣泛應用。盛柏林等[14]沿著某型渦槳發動機的氣路結構進行了部件級建模,并對比了發動機設計點數據和模型性能參數計算結果,驗證了模型的有效性。王元等[15]對變循環發動機建模方法進行了研究,在渦扇發動機性能模型基礎上重新構建了風扇和外涵道模型,并利用NASA試驗數據驗證了模型有效性。王逸維[16]建立了一種三軸拉力式對轉槳扇發動機的仿真模型,其核心機建模采用的是三軸渦軸部件級模型,并基于該模型對槳扇發動機進行了性能評估。以上不同類型發動機性能模型的核心均為利用氣動熱力學描述發動機工作的物理過程,并結合發動機共同工作方程,完成發動機性能模型的構建。
本研究采用變比熱法對某型渦扇發動機進行了部件級建模,并利用臺架測試數據驗證了模型的有效性。將發動機暖機與不暖機2種情況下的實測數據與模型計算值進行對比,分析了暖機對發動機性能模型的影響。
2 發動機部件模型
部件的計算模型是指已知輸入參數,通過氣體動力學和工程熱力學計算出部件的輸出參數。沿著渦扇發動機的氣體流路,對風扇、壓氣機、燃燒室、高壓渦輪、低壓渦輪、混合室、加力燃燒室和尾噴管等部件進行建模,并在尾噴管得到發動機性能的輸出參數。將發動機各部件的計算模型與發動機共同工作方程相結合,就得到發動機的性能模型。本文所用渦扇發動機部件截面如圖1所示。

圖1 渦扇發動機截面示意圖
2.1 風扇模型
定義風扇特性數據中等轉速線上增壓比πc0對應的壓力比函數[17]為:
(1)
式中:πmin為該轉速線上最小增壓比;πmax為該轉速線上最大增壓比。
1) 增壓比πcL、效率ηcL和空氣流量Wa2cor的插值計算
(2)
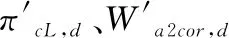
(3)
(4)

(5)
由插值結果的換算流量Wa2cor,求得Wa22:
(6)
(7)

(8)
壓氣機的部件模型具體計算過程與風扇的計算過程相似,不同的是需要增加壓氣機的引放氣。
2.2 燃燒室模型
(9)
式中,σb為燃燒室總壓恢復系數。
2) 油氣比fb和燃燒效率ηb的計算
根據能量平衡和質量平衡公式:
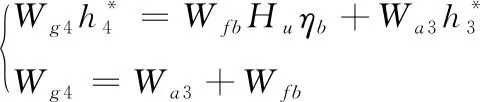
(10)
得到油氣比fb計算公式:
(11)
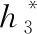
3) 燃油流量Wf的計算
Wf=Wa3fb
(12)
2.3 高壓渦輪模型
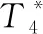
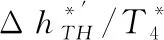
(13)

(14)
(15)
根據換算流量求解出實際流量Wg45,進而求得高壓渦輪功率LTH:
(16)

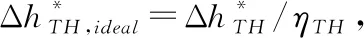
ψ45,ideal=ψ4+Rgln(1/πTH)
(17)
計算求出落壓比πTH:
πTH=[exp((ψ45,ideal-ψ4)/Rg)]-1
(18)
(19)
低壓渦輪具體計算過程與高壓渦輪的計算過程相似,不同的是需要改變冷卻空氣量。
2.4 外涵道模型
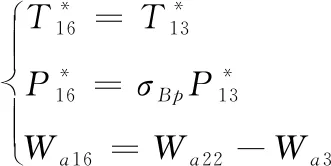
(20)
式中σBp為外涵道總壓恢復系數。
2.5 混合室模型
1) 出口油氣比f6和出口流量Wg6的計算
根據出口燃油流量Wf6=Wg5f5/(1+f5),出口空氣流量Wa6=Wg5/(1+f5)+Wa16,可以求出油氣比f6:
f6=Wf6/Wa6
(21)
出口燃氣流量Wg6:
Wg6=Wg5+Wa16
(22)
(23)
(24)
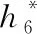
3) 內、外涵入口靜壓P5和P16的計算
根據流量公式和流量函數,可求得入口絕熱指數k5和速度系數λ5。將速度系數λ5和絕熱指數k5代入壓比函數公式:
π(λ)=(1-(k-1)/(k+1)·λ2)k/(k-1)
(25)
求出內涵入口靜壓P5:
(26)
外涵冷流入口的速度系數λ16和靜壓P16計算過程與內涵相同。
流量連續方程:
(27)
動量守恒方程:
(28)
2.6 加力燃燒室模型
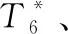
開加力時,計算過程與主燃燒室相同;不開加力時,計算過程為:
(29)
式中,σab為加力燃燒室總壓恢復系數。
2.7 尾噴管模型
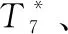
噴管模型為收斂—擴散噴管,其流動過程為絕能過程,相關氣流參數:
(30)
2.7.1設計點狀態
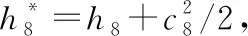
(31)
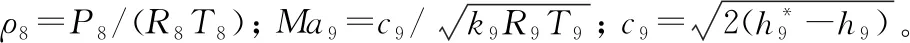
2.7.2非設計點狀態
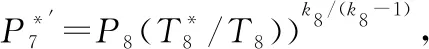
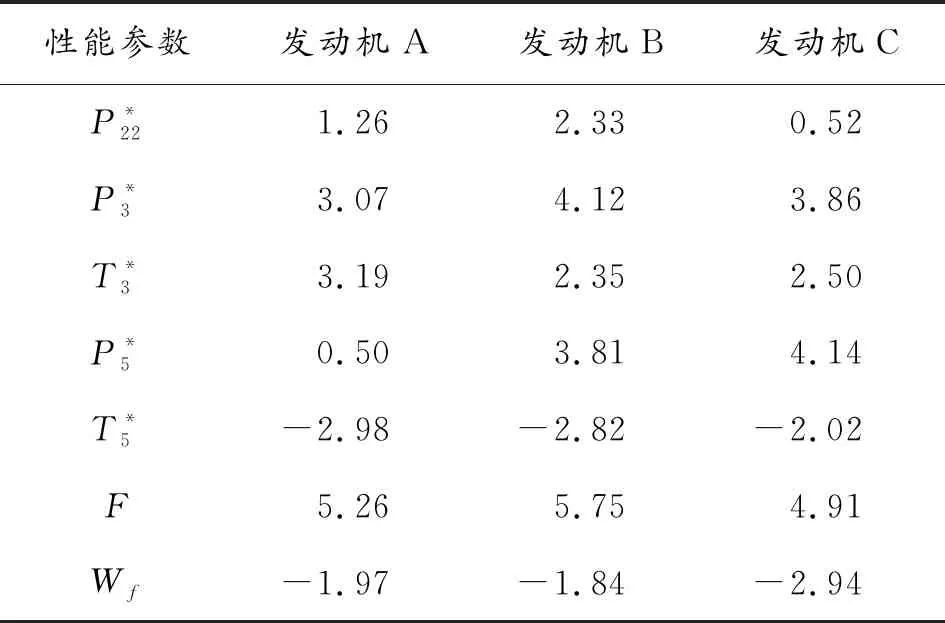
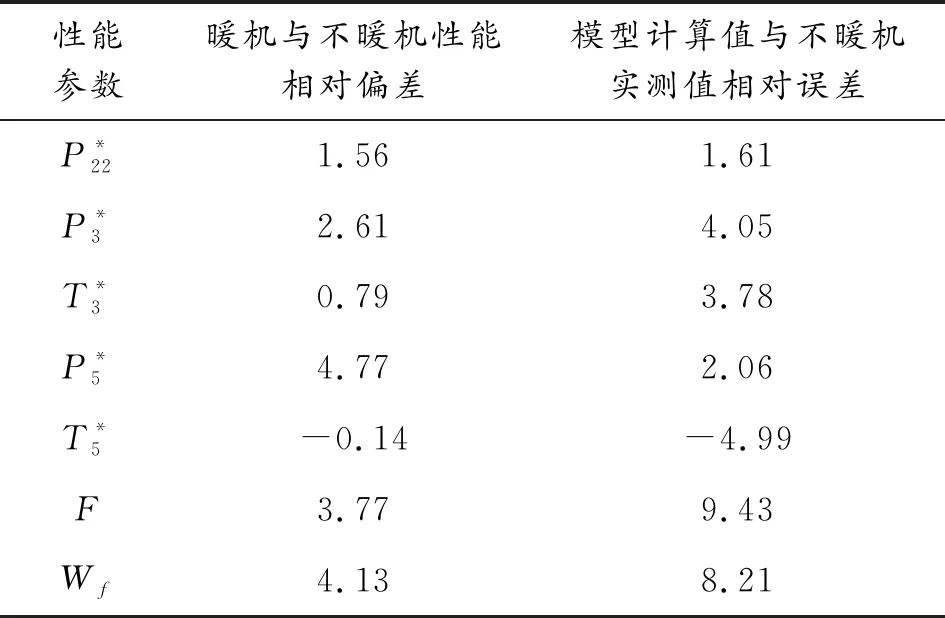
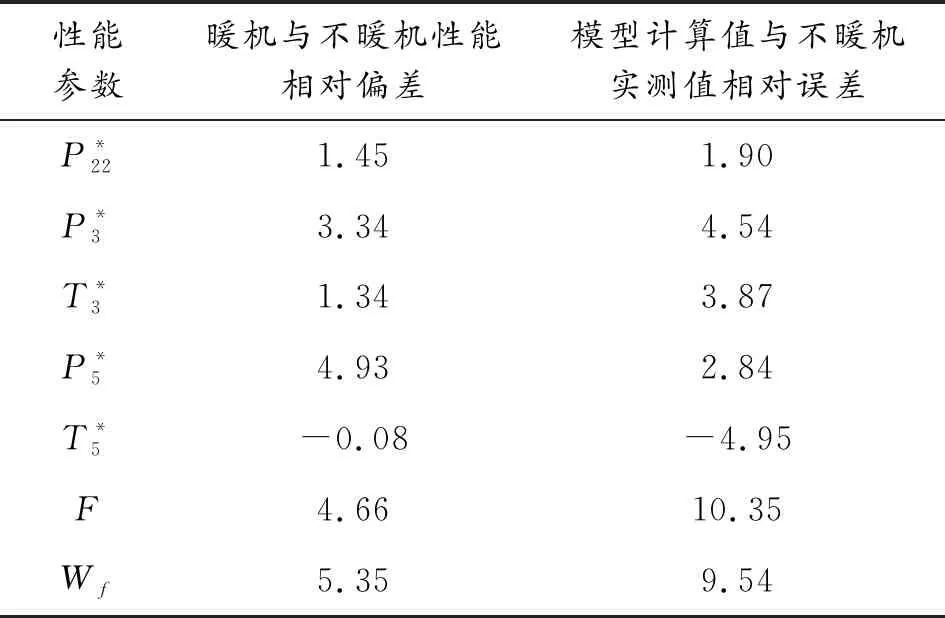
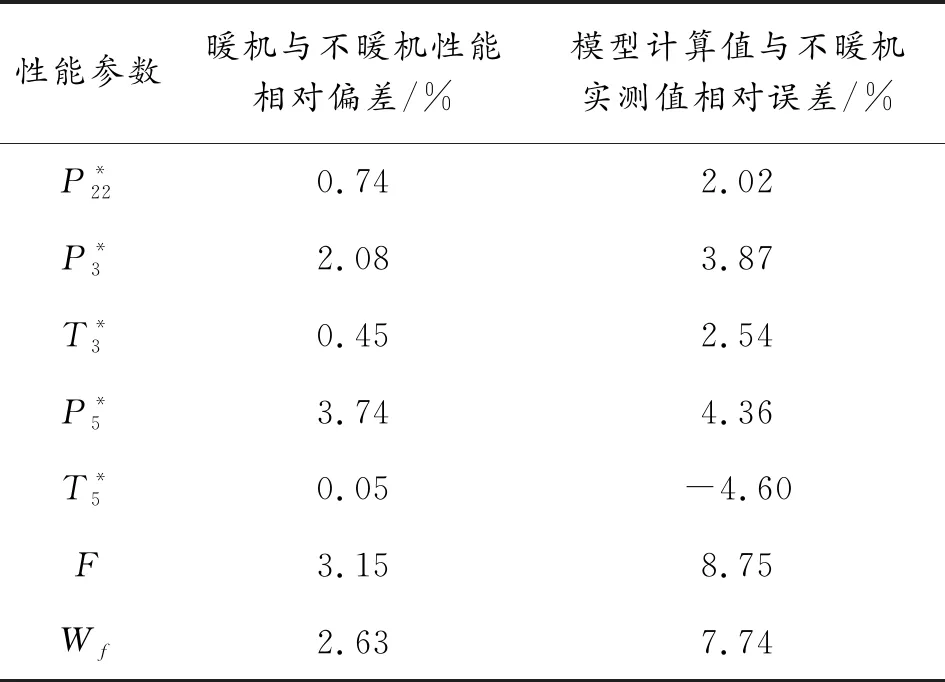
1)P8 重新計算出口靜溫T9,繼而得到出口氣流速度c9: c9=Wg9/[P9/(R9T9)A9] (32) (33) 2)P8≥PH ① 理想完全膨脹 此時A9=A9,ideal,P9=PH。計算過程同設計點相同。 ② 不完全膨脹 ③ 過度膨脹 此時A9>A9,ideal,且在出口將會形成激波。重新迭代計算T9和h9,并計算激波前后的壓力為: (34) 當P9y>PH時,不考慮斜激波的損失,可以近似認為激波前氣流參數就是噴管出口參數。當P9y 2.7.3發動機性能參數計算 發動機推力: F=Wgc9-WaV+(p9-pH)A9 (35) 單位推力: FS=F/Wa (36) 耗油率: (37) 根據發動機共同工作關系,發動機在穩態工作過程應滿足的流量、功率和靜壓平衡方程為: 高壓渦輪流量平衡: (Wa3+Wfb-Wg4)/Wg4=0 (38) 高壓渦輪與壓氣機的功率平衡: (LTH-LcH)/LcH=0 (39) 低壓渦輪流量平衡: (Wa22+Wfb-Wg45)/Wg45=0 (40) 低壓渦輪與風扇的功率平衡: (LTL-LcL)/LcL=0 (41) 混合室入口內涵與外涵的靜壓平衡: (P5-P16)/P5=0 (42) 尾噴口的進口總壓平衡: (43) 發動機部件模型和發動機共同工作方程共同組成了發動機的數學模型,發動機的共同工作點本質就是共同工作方程組的解。因此,發動機數學模型的求解問題就可以轉換為對6個平衡方程所組成的非線性方程組求解問題。發動機非線性模型求解方法通常有牛頓-拉夫遜法和N+1殘量法,本文選擇牛頓-拉夫遜法求解該發動機數學模型: (44) 圖2 發動機模型求解示意圖 選擇該型發動機正常暖機后中間狀態的臺架試車數據作為參考對象,將模型輸入參數中的大氣環境設置為臺架測試環境,驗證上述發動機模型的精度和準確性。將3臺發動機臺架數據和對應測試環境下的模型計算值進行對比,計算結果相對誤差如表1所示。 表1 發動機中間狀態模型計算值與實測值相對誤差 % 從表1中可以看出,性能模型計算值與發動機實測值最大誤差分別為5.26%、5.75%和4.91%,性能模型的最大誤差在5%左右,符合一般情況下的建模精度要求。將表1中各性能參數的相對誤差繪制如圖3。 從圖3中可以看出,3臺發動機性能參數的相對誤差分布基本一致,說明了所建模型的通用性。其中,大部分性能參數都是模型計算值大于實測值。這是由于在建模過程中進行了諸多假設,如:不考慮流道中氣體與各部件之間的熱交換,假設氣體是完全氣體且為一維定常流動等,使得模型的計算過程忽略了發動機實際工作過程產生的一些損失,因此,性能模型的計算結果普遍都偏大。燃油流量和渦輪后溫度比實測值偏小,同樣是由于計算過程忽略了實際工作中諸多損失,從而導致了性能模型可以用更少的燃油產生了更多的推力。 暖機與不暖機2種情況下發動機葉尖間隙會有所差別,不暖機情況下的葉尖間隙大于暖機后的間隙[1]。不暖機產生的間隙變化會直接導致發動機的部件特性發生變化,進而影響發動機的整機性能。 由于暖機與不暖機是針對飛機起飛過程產生影響,而起飛過程中發動機處于最大狀態,因此,本文以發動機最大狀態性能討論暖機影響。 分別對3臺發動機的暖機影響進行臺架試車試驗,獲得發動機暖機與不暖機的性能數據。首先對發動機進行冷推,即發動機在啟動后不暖機直接從慢車一路緩推到最大狀態,得到不暖機的性能數據。然后將發動機油門收回,將發動機狀態降到暖機狀態進行暖機,暖機完成后再次將油門推到最大狀態,得到暖機后的性能數據。用得到的臺架數據進一步計算出暖機與不暖機性能偏差,計算公式為: (45) 式中:Yheating, j為發動機暖機后性能參數實測值;Yunheating, j為發動機不暖機性能參數實測值;j為發動機實測性能參數個數。將3臺發動機暖機與不暖機2種情況下的最大狀態性能實測值進行比較,并將不暖機實測值與模型計算值進行比較,其誤差如表2、表3和表4所示。 表2 發動機A最大狀態相對誤差 % 表3 發動機B最大狀態性能相對誤差 % 表4 發動機C最大狀態性能相對誤差 % 從表4中可以看出,性能模型計算值與不暖機實測值相對誤差較大。在發動機建模的過程中,暖機與不暖機2種情況下發動機的物理過程一樣。但是,由于在建模過程中對發動機進行的諸多假設和簡化處理,使得所建模型只能描述一個狀態,這使得所建模型與真實發動機性能之間存在一些差異,不能描述暖機與不暖機本身存在的性能偏差,導致不暖機情況下模型計算值與發動機實測值相對誤差變大,其最大相對誤差分別為9.43%、9.54%和8.75%,此時原有發動機模型不能準確反映發動機的整機性能。 1) 正常暖機情況下發動機模型精度較高。以3臺發動機的臺架試車數據作為參考對象,將模型輸入中的大氣環境設置為對應發動機臺架測試環境,對比發動機中間狀態的模型計算值與3臺發動機暖機后實測值,其最大誤差分別為5.26%、5.75%和4.91%。性能模型的最大誤差在5%左右,符合一般情況下的建模精度要求,驗證了發動機模型的準確性。 2) 模型性能參數計算值與發動機不暖機實測性能相對誤差較大。由于在建模過程中對發動機進行的諸多假設,使得所建模型與真實發動機性能之間存在一些差異,未能描述不暖機與暖機本身存在的性能偏差。不暖機情況下模型計算值與3臺發動機實測值最大相對誤差分別為9.43%、9.54%和8.75%,此時原有發動機模型不能準確反映發動機不暖機情況下的整機性能。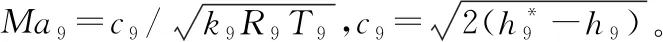
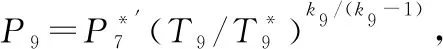
3 發動機共同工作方程
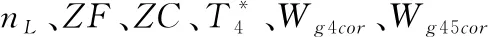
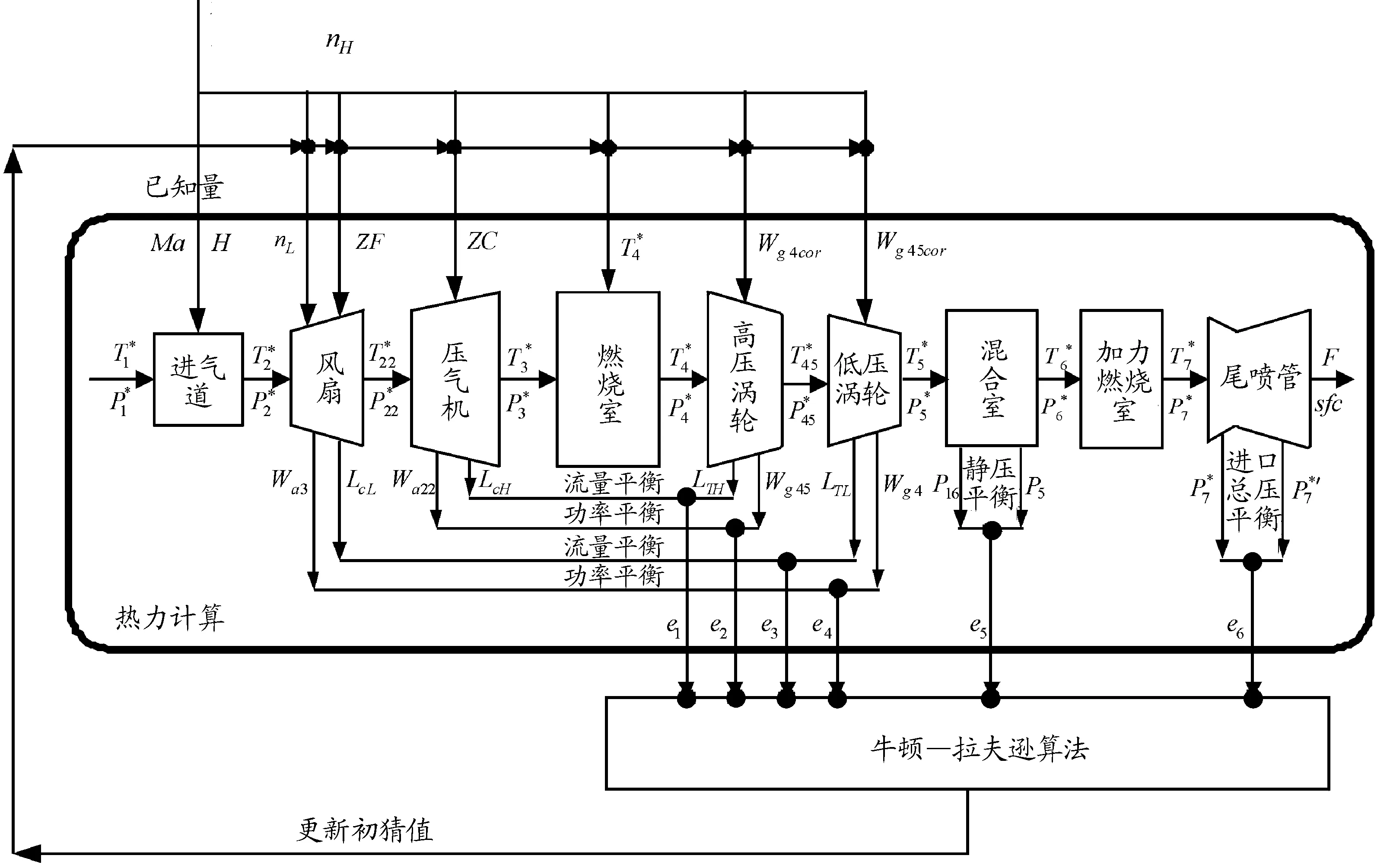
4 模型仿真與驗證
5 暖機對性能模型的影響
6 結論

