探析類比法在高中數學教學中的應用

陳 莉

(江蘇省泰州市泰州中學 225300)

高中數學涵蓋很多的知識點，需要學生深入理解.教學中注重類比法的應用，結合學生熟悉的知識、情境，進行針對性的引導，使學生正確合理的類比，不僅能很好的加深學生印象，而且有助于學生更好的把握數學知識本質，促進高中數學課堂教學效率的明顯提升.

一、類比法用于立體幾何教學

立體幾何是高中數學的重要內容，涉及較多的概念與結論，對學生的記憶以及空間想象能力要求較高.教學中為幫助學生更加清晰的認識立體幾何中點、線、面的空間關系，掌握相關的規律，在解題中靈活應用，應做好充分的教學準備，注重類比法的有效應用.

首先，注重概念的類比.講解立體幾何相關概念時應與學生一起回顧平面幾何知識，如平面幾何中的邊、角與角平分線、圓等.同時，借助多媒體技術為學生展示相關的立體幾何圖形，啟發學生進行類比，使學生對相關的概念有個全面的理解.如可將立體幾何中的面類比為平面幾何中的邊、將二面角及角平分面類比角與角平分線、將球類比圓等.如此既能很好的激發學生的學習興趣，又能使學生更加清晰的認識平面幾何與立體幾何之間的內在關聯.其次，注重性質的類比.立體幾何圖形的性質是高中教學的重要內容，是各類測試以及高考的考查重點，教學中為使學生更好的掌握與理解不同立體幾何的性質，應結合學生已有的知識儲備，引導學生進行合理的類比，降低學習難度，提高學習效率.如在圓中經過切點且垂直于切線的直線必經過圓心，以此可類比出球的相關性質，即，在球中經過切點且垂直于切面的直線必經過球心.在課堂上可給學生留下專門的時間，要求學生嘗試著進行類比，總結相關立體幾何圖形的性質.最后，注重結論的類比.立體幾何圖形中有很多的結論，解題中注重一些結論的應用可獲得事半功倍的解題效果，促進學生學習能力的顯著提升，因此教學中應引導學生回顧所學的平面幾何結論，類比出立體幾何中的結論.

例題如圖1在直角三角形ABC中，∠C=900存在如下結論：①AB2=CA2+CB2；②cos2A+cos2B=1；

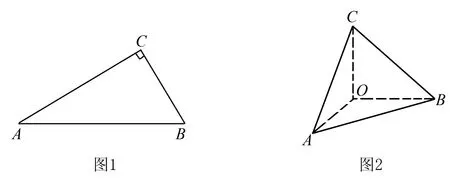
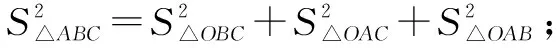
二、類比法用于等比數列教學

高中階段主要學習等差、等比數列，其中學生最先學習等差數列，包括等差數列的概念、性質等.當學生掌握等差數列相關知識時，在進行等比數列教學時可運用類比法開展教學活動，降低學生學習的陌生感，增強其學習等比數列的自信心.運用類比法時應注重以下內容的落實.

其一，鼓勵學生開展自主學習活動.在進行等比數列教學時可結合具體教學內容，給學生預留合理的自主學習時間，要求學生開展自主學習活動.在學習過程中要求學生積極聯系所學的等差數列知識進行合理的類比.同時，注重與學生積極溝通，了解學生自主學習情況，針對學生類比過程中存在的問題，給予針對性的指引，保證其類比的正確性，提高自主學習質量.如在講解等比數列概念時，可要求學生回顧所學的等差數列概念，嘗試著總結等比數列概念，以更好的加深學生印象.同時，通過指引使學生認識到等比數列的首項、公比均不能為零.

其二，結合學生表現給予表揚.運用類比法進行等比數列教學時為提高學生的學習體驗，應注重結合學生的表現給予針對性的表揚，使其嘗到學習的成就感.如在進行等比數列性質教學中，可要求學生結合等差數列中“an=am+(n-m)d”這一性質，通過類比推導等比數列的類似性質，一些學生積極動腦，得出在等比數列中存在的性質為“an=am·qn-m”，顯然類比出的這一性質是正確的.課堂上及時表揚這些學生，使其繼續保持認真學習、積極思考的態度.

其三，借助類比法提升探究能力.教學中發現等比數列的一些習題較為新穎，對學生的探究能力要求較高.教學中為提高學生的探究能力應注重創設新型的問題情景，要求學生進行類比推理，積累探究的經驗與技巧，更好的解答類似的探究問題.

三、類比法用于向量教學

向量在高中數學中占有重要地位，知識點多而零碎，對學生的記憶力要求較高.向量知識應用廣泛，可作為解答其他數學習題的重要工具.教學中為使學生牢固掌握向量知識，并能在解題中靈活應用，為學生數學學習成績的提升奠定堅實基礎，應注重類比法在教學中的應用.

一方面，講解向量相關概念時，為使學生更好的理解，應注重引導學生聯系所學的實數知識，進行正確的類比.如在講解向量的模這一概念時，可使學生將其與實數的絕對值進行類比.通過類比學生能夠深刻的認識到向量的模為正或者為零，但絕對不為負.如此可為其更加深入的學習向量知識做好鋪墊.另一方面，向量有很多的運算規律，一些學生常將其與實數的運算律混淆在一起，在解題中張冠李戴.教學中為使學生更好的掌握向量運算律，應引導學生將向量運算律和實數運算律進行正確的類比.如實數中存在交換律、分配律，通過類比可得到向量的交換律、分配律，以下結論是成立的：①a+b=b+a；②a·(b+c)=a·b+a·c；一些學生通過類比實數的乘法結合律，得出向量的乘法結合律為：(a·b)c=a(b·c)，經驗證這一類比結論是錯誤的.由此啟發學生在類比的過程中還應進行驗證.另外，在進行空間向量知識教學中，可引導學生將其與平面向量進行類比，更加深刻的理解空間向量的計算過程以及計算結論.如已知平面向量a=(x1,y1)，b=(x2,y2)，則其坐標運算為a+b=(x1+x2,y1+y2)，通過類比可得出空間向量的坐標運算為a=(x1,y1,z1)，b=(x2,y2,z2)則a+b=(x1+x2,y1+y2,z1+z2).

四、類比法用于圓錐曲線教學

圓錐曲線是高中數學的重點難點，相關習題計算量較大.教學中為提高學生的解題效率，使學生在解題中少走彎路，應注重運用類比法開展教學活動.教學中既要注重引導學生新舊知識的類比，又要注重圓錐曲線之間的類比.通過類比得出相關結論，直接用于解題中.

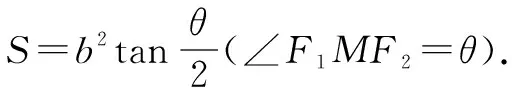
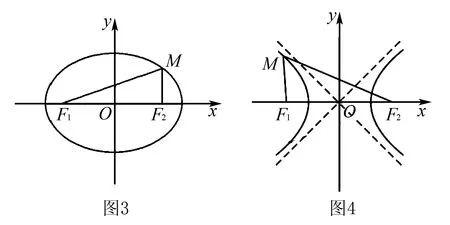
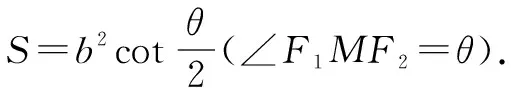
類比法是學習以及研究新問題的重要方法之一.通過類比可使學生在學習中少走彎路，更好的掌握數學知識本質，在解題中以不變應萬變.高中數學教學中既要為學生講解類比，發現相關理論，又要圍繞教學內容積極創設相關的問題情景，啟發與引導學生進行類比推理，尤其鼓勵學生應用類比法注重相互交流經驗，不斷學習他人長處，不斷的充實與提升自己.