簡約 辨析 說理 層次

王冬暉

深度學習，是在教師的引領下，學生圍繞具有挑戰性的學習內容，使其積極參與、體驗成功、獲得發展，旨在引導學生掌握學科的核心知識，把握學科的本質及思想方法。本人結合人教版《義務教育教科書·數學》三年級下冊“口算除法”的教學實踐，通過精巧設計課堂教學環節，搭建探究建構平臺，幫助學生分析不同算法中算理的內在聯系，突出口算除法的算理內涵，展開知識聯結、整合，充分發揮了學生的主體性，搭建了探究建構平臺，培養學生的運算能力，最終學生的素養得以落地。

一、夯實基礎——簡約中突顯本質

布魯納認識發展理論指出：學習本身是一種認識過程，個體的學習總是要通過已知的內部認知結構，對“從外到內”的輸入信息進行整理加工，以一種易于掌握的形式加以儲存。這就需要我們關注新舊知識的連結點和學生的學習起點。

在 “口算除法”的導入時：

師：今天這節課老師跟大家一起學習“口算除法”，這道題會算嗎？

生（齊）：6÷3=2

師：你是怎么想的？

生1：二三得六，6÷3=2（利用乘法口訣解決）

生2：把6個蘋果平均放在3個籃子里，每個籃子放2個（借助生活經驗解決）

……

以上新課引入的片段，雖略顯簡單，但能簡約明了地進入學習主題。本節內容“口算除法”是學生首次接觸“表外除法”（不能直接用乘法口訣求商）。此設計，教師順應學生的學習起點，重點復習“表內除法”口算方法，為學習新知鋪墊，更加夯實了學習新知所必要的基礎，這樣不僅能讓學生在新舊知識對比中，引發新舊沖突，促使學生主動探索口算除法的過程，親身經歷探究過程，而且有利于自主歸納口算方法，增強對表內、表外除法的直觀感受打好基礎。這樣的引入充分體現了新舊知識間的密切聯系，溝通知識脈絡，同時為本節課后續深入探究新知節約了寶貴的時間。

二、多元表征——辨析中悟出道理

數學多元表征是指對數學素材的多元化的呈現，是數學語言化、視覺化等不同體現，它是學生進行數學學習的載體，也是數學學習常用的方法。數學的多元表征不僅能促進學生對數學知識本質的深刻理解，還可以促進數學活動經驗的積累以及良好數學結構的建立。

在“口算除法”的新知學習中：

教師通過“60÷3=20”，引導學生思考：為什么等于20？讓學生采用同桌合作方式或選擇自己喜歡的方式或借助老師提供的學具等自主選擇等靈活學習形式來驗證60÷3的結果。

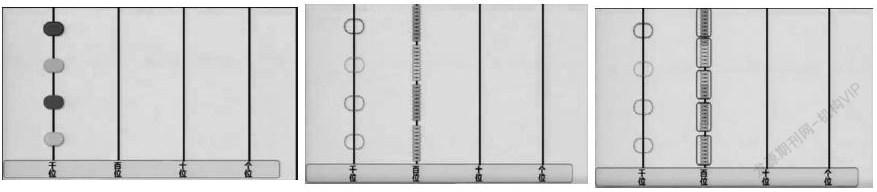
學生上臺分享想法：

操作法驗證（圖1）：選擇用整捆的小棒來分。一捆小棒有10根，把6捆小棒平均分成3份，每份是2捆，就是2個十。

借助法驗證（圖2）：借助計數器來表示。先在十位上撥6顆珠子，表示6個十。平均分成3份，每份就有2顆珠子，就是20。

替代法驗證（圖3）：有6根小棒。每根小棒代表10，把它們平均分成3份，每份就是20。

圖示法驗證（圖4）：我用畫圖的方法。一個圓圈表示10，6個圓圈就有60，平均分成3份，每份就是20。

學生展示分享匯報完之后，教師接著追問：為什么選擇的學具不同，可是結果卻相同？學生思考后得出：“60÷3=20”表示 60就是6個十，除以3表示平均分成3份，結果每份就是20。

小學生的思維特點以形象思維為主，尤其是低年級的學生，他們需要在活動中經歷知識和發展的過程。而操作感知是學生認識數學的重要方式，在操作經驗的基礎上產生不同的表征。教師提供多樣的學具，學生自由選擇表征算理的方式，不同學生呈現的思維形式不同，在表征過程中積累不同經驗，在算理和算法間游離變化，形成計算的認知結構，為理解數學本質打下基礎。本環節設計引導學生自主通過實物、圖形、符號等對60÷3=20的結果進行表征，學生在同與不同的辨析過程中，深刻理解感悟獲得結果的道理，即解決問題方式利用的材料不同，表征的方式也不同，但殊途同歸，不僅獲得了結果，而且獲得了更為廣闊的解題思路和經驗，利于發現“口算除法”背后的“深層算理”。

三、巧設問題——說理中深刻領悟

問題是激發和引領課堂教學的重要推手，是撬動學生思維的杠桿，是驅動學習任務的開始，是師生之間進行知識和情感傳遞的重要載體。思維源于問題，數學的深度學習是基于問題的學習。學生在探索解決問題的過程中，通過觀察、發現、說理、比較等學習方式，使數學知識的理解更加深刻，數學能力與數學思維也得以提高。

在解決了“60÷3”新知學習后，教師設計了以下問題：

問題一：把計數器十位上的6顆珠子移到百位，平均分成三份，每份是多少？怎樣列式？

問題二：如果不撥珠，只列算式你們會算嗎？（600÷3=200）

問題三：像這樣繼續往下寫，還能寫幾個？（師板書6000÷3……）

問題四：仔細觀察這些算式，有什么發現？

學生帶著問題思考學習，問題把學生的思維一步步引向深入。通過觀察、說理、發現：這組算式可以先算6÷3=2，再看被除數中有幾個0，商再添上幾個0。這樣的問題串，為學生搭建了自主探索的學習平臺，意引導學生經歷“幾個十÷3”——“幾個百÷3”——“幾個千÷3”，甚至是“幾個萬÷3”的變化過程以及得數的變化規律（建立模型），通過表達說理完成由知其然向知其所以然的和諧過度，深刻領悟算理本質，同時數學能力與數學思維得以提高。

四、對比抽象——層次中完善建構

數學知識是一個充滿聯系的體系，運算教學更是如此，每個知識之間都有著內在的聯系區別。本節課的教學內容，不僅要讓學生從外在（形上）掌握其求得結果的特殊特征（特殊性），更為重要的是要讓學生領悟其求得結果的一般特征（一般性）即本質特征，為此，必須進行在特殊性的基礎上進行對比變式，從而使學生真正理解領悟算理的本質屬性。