基于DEM克里金插值模型選取及參數計算研究
——以青海省可可西里五道梁地區為例

白冰源，程耀瑜

（中北大學，山西 太原 030051）

0 引言

對于某地區溫度和降水分布插值，可基于ArcMap中的插值分析工具快速實現，目前主流教材對于該類課題則多用反距離權重插值算法（IDW)[1]，然而由于IDW的內插單元值需要針對鄰近區域采樣點進行平均值運算，故需要使得樣本點在空分布上滿足均勻分布。對此，筆者認為在一些實際問題應用中并不能很好滿足上述條件，例如青海省可可西里等偏遠地區氣候惡劣，人跡罕至，且一般面積廣闊，雖然有氣象數據收集站，但數量稀少，難以均勻覆蓋；因此為了解決該類地區數據插值問題，筆者就反距離權重插值算法與克里金插值算法做以比較，并對更為合適的克里金插值算法深入研究分析。

1 研究思路

1.1 反距離權重插值算法（IDW）

IDW（inverse distance weighted）是從插值點與樣本點之間提取距離參量，以此為權重進行加權平均，所賦權重值與距離參量成反比關系。該算法的基本思路是根據周圍離散點的值，通過距離加權來計算點Z的值；故我們可假設一系列離散點分布在平面上，并通過實際測繪得到樣本點的坐標和具體數值為，即有：

1.2 克里金插值算法

克里金插值法又稱空間局部插值法，是基于變異函數理論和結構分析，針對邊界區域的區域變量進行無偏最優估計的主要方法之一[2]。最初于1951年由南非的工程師D.R. Krige首次實踐應用，隨后由法國著名數學家G. Matheron[3]將該方法理論化、體系化，稱為krigine（克里金法）。

在本課題中，克里金法的實質是結合待測地區氣象數據站點的空間方位，指定地理區域的降雨和溫度數據，通過GS+軟件分析所得到的變異函數關鍵參量，以及待插值樣本點的空間位置關系等多個方面，來對未知樣點進行線性無偏、最優估計。其中無偏是指數學期望為零的偏差值，最優是指估計值與實際值之差的平方和最小[4]。

可以簡單表達為

式中，s為待測區域空間坐標點；Z(s)為s處所對應的變量函數值，可分解為確定趨勢值μ(s)和自相關隨機誤差ε(s)，通過對該公式的參量進行不同變化，即可得到多種類型的克里金插值算法[5]。

1.3 兩種插值法異同

（1）相同：兩種算法實現方式均是通過對已知樣本點賦權重值，從而求得未知樣點的值，可統一表示為：

在本課題中，Z(x0)為待插柵格的降雨和溫度的數值；Z(xi)為待插柵格有限空間范圍內已知的氣象站數據；λi為第i個柵格的插值權重；n為已知氣象站數據采樣點的數目。

（2）不同：反距離權重插值方法在賦權重時，僅考慮已知樣本點與待測樣點的距離遠近[6]，而克里金法則結合了變異函數等多個參量信息，尤其是從空間方位上考慮了已知樣本點和待測樣本點兩者的位置關系[3]，故從實際應用角度來看，普通克里金法的插值結果要優于距離加權反比法的插值結果[7]。

1.4 實驗變異函數值

在二階平穩假設的基礎上，有實驗變異函數值的計算公式：

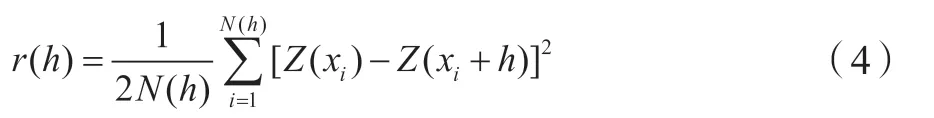
本課題求解實驗變異函數需要以下幾步：（1）選定樣本空間中的某一方向；（2）設定基本滯后距h，該數值一般取空間中各樣本點的基本間距；（3）根據計算得到的不同空間距離h下的實驗變異函數值，再選擇合適的變異函數模型進行后續擬合[8]，進而找到適合分析本課題中所提出的可可西里地區的最優函數模型。

1.5 變異函數模型的參數擬合

為了可以對空間中任意點處的溫度，降水量數值進行估計，需要找到一個合適的理論變異函數模型來擬合所求得的一組實驗變異函數值r(h)。本課題利用GS+軟件探究最優模型，并在ArcMap中進行后續插值。

2 變異函數球狀模型

根據模型結構特點，變異函數理論模型主要有基臺值模型、無基臺值模型以及孔穴效應三大類[9]。本課題研究對象主要是有基臺模型中的球狀模型，因此對球狀模型進行重點介紹，球狀模型的一般公式為：

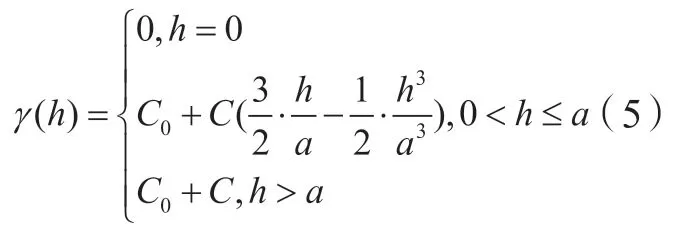
式中，C為拱高；C+C0為基臺值；a為變程參數。

當h=a時，(h)≈C+C，因此，該模型變程A≈a。對模型做均值為0，方差為1的標準化后，有，此時該模型稱之為標準球狀模型。

3 具體操作

本課題以實際工作中最常見的球狀模型、指數模型、高斯模型為理論基礎，通過軟件分析這三種模型在變異函數擬合及克里金插值過程中的差異，并選取最優結果。

3.1 最優變異函數選擇及參數計算

將數據導入GS+中.可得該組數據克里金插值最適的變異函數模型為球狀模型，故進行GIS插值時選擇球狀模型；并且同時可以得到插值最優參數。

3.2 GIS克里金插值

針對上述GS+分析數據，現利用ArcMap進行克里金插值，結果如圖1、圖2所示：

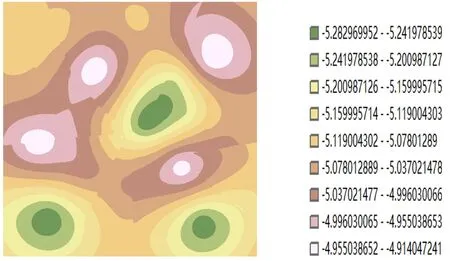
圖1 溫度數據克里金插值結果

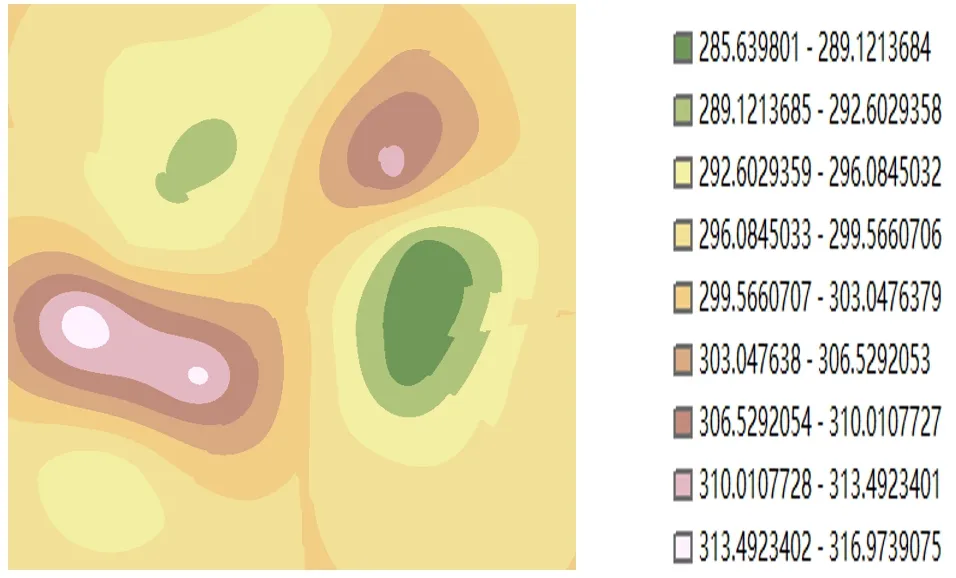
圖2 降水數據克里金插值結果

利用得到的溫度，降水插值結果，進行二值化處理；之后提取滿足該植物生長的4個適合區域并取交集，結果如圖3所示，淺色部分為最適生長區域。

圖3 克里金插值法得出的最適生長區域

4 結語

本課題基于DEM數據，對《基于DEM的青海省可可西里五道梁地區某瀕危植物生長分布預測》論文中所用的IDW算法，選擇采用克里金插值法進行優化；并利用GS+軟件計算得關鍵克里金插值參數，在ArcGIS中實現插值，得到更精確的預測生長結果。