股票價值評估：Gordon增長模型還是ZZ增長模型

摘 要：科技創新和資本市場的發展，凸顯了股權或股票價值評估的重要性。目前流行的評估基本無外乎應用Gordon增長模型的絕對價值評估，以及應用市盈率等評估比率方法的相對價值評估。然而，深入分析發現，Gordon增長模型實際上沒有應用可行性，而評估比率方法沒有理論合理性。多方面比較分析發現，ZZ增長模型（至少）與Gordon增長模型有同樣的理論合理性;同時可以容忍一定的參數估計誤差，有應用可行性。基于ZZ增長模型推導出的三個理論比率模型，可以從根本上改進評估比率方法缺乏理論合理性的缺陷。不僅如此，ZZ增長模型特別適合評估目前兩大方法都不擅長的高增長的股票，這意味著作為ZZ評估系列模型的ZZ增長模型以及ZZ理論比率模型在互聯網和高科技公司的價值評估中大有用武之地。

關鍵詞：股票價值評估;Gordon增長模型;ZZ增長模型;每股紅利;每股收益;市盈率

中圖分類號：F830.91? 文獻標識碼：A

文章編號：1000-176X（2021）07-0074-10

一、引 言

科技和歷史的進程決定了這是一個不平凡的時代。科技與資本相互推波助瀾，成就了波瀾壯闊的創業浪潮和群星璀璨的明星公司。伴隨各種新行業、新業態和新公司的興起以及另外一些行業和公司的衰退，是彼伏此起、經久不息的公司并購熱潮。科創板于2019年6月在上海開市交易，一年以來漲勢兇猛，讓人們見識了科技、資本與實業結合的力量[1]。資本借助科技而加速雪球效應，實業借助資本而扶搖直上……

而這科技與資本的盛宴狂歡也帶動了人們對公司股權價值的關注。公司并購和股票上市其實都是股權的買賣，就像買賣其他東西一樣，買賣股權需要知道其價值多大。因此，股權或股票價值評估以及評估模型成為股票和資本市場關注的焦點。

股權或股票與公司債務資本相對，都是公司的權益資本，上市公司多稱股票，非上市公司多稱股權。因而，股權或股票價值評估也沒有區別，最終都是得出某公司一定比例的股權價值為多少的結論。因此，本文中根據表達的方便可能不加以區分，交替使用股權價值評估或股票價值評估。

Gordon[2-3]增長模型也稱為股利增長模型或常態增長模型，是長期以來股權和股票價值評估領域盡人皆知的模型，是眾多世界級商學院財務管理、證券投資、投資銀行、風險投資等金融相關課程中不可缺少的主角，也在華爾街、倫敦、新加坡、中國香港、上海、深圳等世界知名股票市場中發揮著不可缺少的作用。

除去各種投資分析以及選股方法不論，就能計算股票價值的模型而言，除了Gordon增長模型，還有什么模型呢？在投資分析報告里翻，在流行金融教科書里找，難覓其他模型的蹤影。其他模型即便有，往往是這個模型的某種變型，如將股票紅利換為另一個收益指標如股權自由現金流量、包含Gordon增長模型的兩階段模型或多階段模型[4-5]等。因此，Gordon增長模型不僅是股票價值評估中的主角，而且基本在其中唱獨角戲。

本文拿來比較的ZZ增長模型[6]-[8]，在知名度和流行性方面，完全無法與Gordon增長模型相提并論。然而，畢竟有比較才有鑒別。事實證明，知名度和流行性往往說明不了正誤與好壞。在哥白尼時代，地心說在知名度和流行性上都占壓倒優勢，但最終人們還是明白了其顛倒性錯誤，而正確的正是當時不知名不入流的日心說。

無論如何，有可供比較的模型是好事，起碼有助于擇優應用。當然，萬一經過分析發現Gordon增長模型確實靠不住，則ZZ增長模型也許是解決和解答股權或股票價值評估的希望所在;倘若如此，也算是本文對金融理論與實踐的貢獻了。

二、模型及其理論合理性

Gordon增長模型將股權價值看做是未來現金流量（即紅利）的總現值，ZZ增長模型將股權價值看做是未來要求回收期內股權或股票收益的非折現價值總和，這里的股權收益包括紅利和留存收益即凈收益，在每股的口徑上即是每股收益。

（一）模型形式與自變量

Gordon增長模型為：

P=D1+gk-g=D1k-g（1）

其中，D為當前年度每股紅利（如果評估股權總價值則為紅利總額）;g為紅利永續增長率;D1為明年每股紅利，因而有：D1 = D（1+g）;k為投資者要求收益率即貼現率。可以理解，運用Gordon增長模型，估計的增長率g必須小于貼現率k。

ZZ增長模型為：

P=1+gn-11+gE/g=1+gn-1E1/g（2）

其中，E為當前年度每股收益（如果評估股權總價值則為收益總額）;g為收益（總收益或每股收益）在可預見時期（一般10—20年）的增長率;E1為明年每股收益，因而有：E1 = E（1+g）;n為投資者要求回收期。可以理解，要求回收期是要求收益率即貼現率的倒數。比如，投資者要求收益率為10%，即意味著按照這個要求，每年可以收回初始投資的10%，從而收回全部投資需要10年，即等于1/10%。

兩個模型都是嚴格邏輯推理得出的模型，且都是封閉解模型。推導過程數學上都較為簡單，屬于簡單的初等數學應用。兩個模型有一個一目了然的區別，Gordon增長模型中增長率g的取值有嚴格限制，不能大于或等于貼現率k;而ZZ增長模型中增長率g的取值基本沒有限制，取值為正、為負，以及取值很大，都可以。

（二）模型的理論合理性

符合邏輯是得出正確結論的前提。嚴格邏輯推理有利于保證模型的正確性，數學上簡單也便于檢查和保證推理過程不出差錯。可以說，兩個模型都是從基本概念出發經過嚴格推理得出的結論，邏輯和定量推導過程至今沒有發現差錯。

兩個模型都是綜合考慮風險和收益得出股票價值。Gordon增長模型借助每股紅利D及其增長率g考慮收益，D和g越大，則收益越大;借助貼現率k考慮風險，k值越大，風險越大。ZZ增長模型借助每股收益E及其增長率g考慮收益，E和g越大，則收益越大;借助要求回收期n考慮風險，n值越小，風險越大。

在Gordon增長模型中，D和g越大，計算得出的股票價值越大;而k值越大，計算得出的股票價值越小。類似地，在ZZ增長模型中，E和g越大，計算得出的股票價值越大;而n值越小即風險越大，計算得出的股票價值越小。這意味著，兩個模型都表明價值與風險負相關，與收益及其增長正相關。顯然，兩個模型都是綜合考慮并合理權衡了風險與收益，符合風險與收益決定價值的基本公理，具備理論合理性。

（三）自變量的估計難度

Gordon增長模型要考慮未來很長時期，確切說是無限長時期的情況;而ZZ增長模型只考慮未來有限期中的情況，確切說是可預見時期中的情況。也就是說，Gordon增長模型中的變量估計結果應該要求在無限長時期中有效或合適，而ZZ增長模型中的變量估計結果只要求在有限長時期即大于或等于要求回收期的時間中有效或合適即可。

由于不考慮有關變量隨時間而變化，這里的有效或合適是指估計值應該等于或接近于相應時期中的平均值。可以理解，需要符合或適用的期限不同，變量估計的難度就不相同。Gordon增長模型需要適用的周期長（長很多），因而變量估計的難度大;而ZZ增長模型需要適用的周期短（短很多），因而變量估計的難度小。

同時，具體變量差異也導致估計難度不同。E的估計難度小于D，而n的估計難度也小于k。難度的差異可能直接導致估計結果的質量差異，而且無法通過努力來彌補這種差異。比如，D受所有影響E的因素的影響，同時還受公司分紅政策的影響。由于這個差異，E的取值及其變化直接代表公司的業績或收益情況，但D的取值及其變化可能并不反映公司的業績或收益情況。同樣是增長率，ZZ增長模型中的g是短期中的增長率，而且取值不受限制;相反，Gordon增長模型中的g是無限長期中的增長率，而且取值要嚴格小于k。因而估計Gordon增長模型中的g要比ZZ增長模型中的g難得多。

比如，根據年報數據，包括股權變動調整，過去20年中，海爾每股收益年均增長率為16%左右;假定分紅比率基本不變，則股票紅利增長率也是16%左右。海爾作為我國知名家電公司，其股票基本屬于我國A股市場的藍籌股。基于我國股市和美國股市的經驗[9]-[12]估計，這類股票的合理收益率或適用貼現率應該不超過10%，這意味著如果運用Gordon增長模型，對于海爾未來無限長時期中每股紅利的增長率的估計值應該不超過10%。時間跨度如此之大，如何在不超過10%的范圍內估計出這個增長率呢？

海爾畢竟主體上算傳統行業的公司，換作高科技高增長的公司，如果運用Gordon增長模型，那增長率的估計就更是難上加難了。比如騰訊公司，自從在中國香港上市以來，16年中收益年均增長率大約為45%。假設經過估計，其合適貼現率為15%，如何估計出一個適用于未來無限長時期的增長率，而這個增長率又必須小于15%呢？

當然，如果應用ZZ增長模型，增長率的估計就簡單和容易得多，因為只考慮相對短期（如10—20年）即可;特別方便的是，模型對增長率的取值沒有限制，超過10%、20%甚至50%、100%都沒關系，只要符合相應公司未來增長的情況即可。當然，可以理解，收益預測符合實際情況是所有模型的共同要求，不是該模型的特殊或額外要求。比如，估計海爾今后可預見時期中每股收益的平均增長率為10%—20%，或者騰訊今后可預見時期中每股收益的平均增長率為20%—50%，代入該模型運算都沒有問題。

綜上所述，ZZ增長模型中的自變量估計難度明顯小于Gordon增長模型。不僅如此，ZZ增長模型是真正名副其實的增長模型，因為它可以將任何增長率的取值轉化為相應的股票或股權的價值。對比而言，Gordon增長模型似乎名不副實;模型似乎害怕增長，公司增長率稍微高一點，Gordon增長模型就喪失計算能力，無法應用。

應該明白，兩個模型中的常數或不變增長率g并不要求紅利或收益穩定增長，而是代表未來相應時期中的平均或年均增長率。將年均增長率改為具體逐年預測的增長率將大量增加模型中自變量的個數。對于ZZ增長模型而言，這將增加自變量預測以及模型應用的難度;而對于Gordon增長模型而言，則將使自變量的個數增加到無窮多，從而也就不僅是增加難度的問題，而是直接將模型的應用可行性降低到零。

因此，兩個模型中自變量作為不變的常數代表的是平均值，這不但不是模型的缺點，相反，正是模型的優點。按照平均值來估計或預測不僅確保了模型的簡明，也確保了模型的應用可行性。現實中有人誤以為模型要求公司在未來保持勻速增長，甚至有人提議改正這個不符合實際的“缺點”，實屬理解上的欠缺。

三、模型的應用可行性

不妨設想簡單的數字例子試算一下。

例如，預計股票A、B、C明年的每股紅利都為1元，未來長期中年增長率分別為8%、9%、9.5%。三家公司風險相當，估計的股權適用貼現率都為10%。

基于這些信息，可以應用Gordon增長模型計算股票價值為：

PA = 1/（10%-8%） = 50元，

PB = 1/（10%-9%） = 100元，

PC = 1/（10%-9.5%） = 200元。

請注意，上述舉例用意不在說明如何使用Gordon增長模型，也不說明Gordon增長模型有應用可行性，而是通過具體的計算測試一下模型有無應用上的問題。

可以發現，模型的確有應用問題，計算結果對增長率g非常敏感，一個百分點甚至半個百分點的差異就導致得出的股票價值相差一倍。當然，計算結果對自變量取值非常敏感不一定說明模型不好。準確地說，這說明模型要求應用時對增長率的估計要非常準確，因為增長率上一個或半個百分點的誤差都會導致評估結果的倍數差異。

如前所述，這個增長率的確切概念是股票紅利的永續增長率，也就是未來無限長時期中的平均增長率。這樣的長期增長率預測本身就很難，現在又要求非常準確，自然是難上加難。試想，有誰可以非常準確（比如誤差不超過0.5%）地預測一家公司未來無限長時期中股票紅利的年均增長率呢？

由此判斷，Gordon增長模型并不可靠，或者說，應用可行性不大。進一步分析可以發現，Gordon增長模型還有更致命的問題。不妨思考一個現實問題：已知海爾2019年每股收益為1.29元，分配方案為每10股派發現金股利人民幣3.75元，即每股分紅0.375元。以此為起始點，請問1萬年后，海爾的每股紅利為多少呢？結果如表1所示。其實，雖然課堂教學中反復講，實踐中反復用，但沒有多少人有足夠耐心計算過這樣的問題。

按照Gordon增長模型的永續增長假設，回答這樣的問題需要先預測年均增長率。如前所述，模型要求這個增長率的預測必須非常準確，但無論如何，現實中不同的人預測結果會有差異。表1中的增長率也許代表最為保守的預測，即扣除通貨膨脹后的實際增長率取1%和2%，這可能低于絕大多數人的預測。為避免計算結果數字太大，已經換算為萬元，即相當于初始每股紅利為0.0000375萬元。但即便如此，表1中計算得出的每股紅利還是大得驚人，估計出乎絕大多數人的想象。

業內人士都知道，實踐中應用時這個增長率的取值往往都更大。在很多人看來，像海爾這樣的藍籌股取永續增長率為5%不算樂觀，甚至是非常保守的估計了，像表1中1%、2%這樣的增長率只能屬于股市中最差的少數上市公司，這意味著實踐中的預測比表1顯示的數字還要大得多。也就是說，在Gordon增長模型考慮的周期內，用不著到10 000年，絕大部分上市公司的每股紅利都會變為天文數字。這樣的未來收益“預測”可信嗎？如果不可信，如何相信基于這樣的預測得出的股票價值即Gordon增長模型評估的結果呢？

也許有人會說，今天存在的公司，無論多么紅火多么穩健，10 000年后可能都不存在了，管它預測得對不對呢。然而，如果肯定或大概率確定是不存在，那就意味著每股紅利為0，而不是更大的數字。到底是0還是更大的數字或天文數字，這個問題不能含糊，因為誤差太大了！

也許有人會說，這里的每股紅利數字再大，折現到10 000年，價值也幾乎為0。但是，這樣的說法也不能成立。預測和折現是價值評估中的兩大工作，預測是預測，折現是折現。折現不是掩蓋預測錯誤的工具或擋箭牌。不能因為后面有折現計算，前面的預測就無所謂，就可以將年均增長率為2%情況下，海爾第10 000年的每股紅利等同于0元。可想而知，這樣的誤差在預測中是不允許的，在任何定量理論與實踐中也都是不允許的。

也許有人會說，隨著每股紅利的增大，公司將采用拆股或類似操作，即通過增加股票股數減少每股紅利，使其達到一個適宜的數值范圍，比如達到現在常見的范圍1—10元左右。這樣，就不會有上述天文數字的每股紅利了。但顯然，這個想象也無法成立。因為既然每股的紅利都達到了天文數字，那每股就要拆分出天文數字的股數，才能使每股紅利回歸正常范圍，再乘以公司目前的股數，比如10億股。那就是股票股數為10億個，即更大的天文數字。這樣，到未來足夠長時間，不是每股紅利為天文數字，就是股票股數為天文數字。當然，無論哪個指標為天文數字，都是不正常的情況。其實，在運用Gordon增長模型評估股票價值時，需要通過調整消除拆股或類似操作的影響;也就是說，拆股或類似操作本來就不必在評估時加以考慮。

因此，對于永續或長久增長的假設稍做分析可以發現，Gordon增長模型很難自圓其說。

不僅如此，上述探討又牽扯出Gordon增長模型的另一個問題。既然在考慮的時間周期內公司必然消失，這就意味著任何形式的收益，無論是每股紅利還是每股收益，也都將變為0。從現在的正收益，到未來的零收益，如果要計算平均增長率的話，只能為負數，而不是如目前業內想當然認為和使用的正增長率。上述表1的計算中使用1%、2%這樣很低的正增長率都得出不可思議的每股紅利天文數字，也佐證了負增長率的合理性。也許短期內公司可以保持正增長，甚至有較高的增長率，但在足夠長的時期中，不存在保持連續或平均正增長的可能性。由此可知，多數價值評估與投資分析報告都值得存疑。

即便這個發現不是結論，而是悖論[8]，也至少說明，至今為止，金融領域沒有搞清楚長久或永續增長率究竟是正是負。前面分析已經說明，Gordon增長模型要求應用時估計的增長率必須非常準確;現在又發現，這個增長率其實是正是負都搞不清楚。由此可知，Gordon增長模型其實完全沒有應用可行性。誰也不能在正負都搞不清楚的情況下，準確估計一個變量的取值。一個完全沒有應用可行性的模型在全世界廣泛傳播和應用，甚至成為唯一的股票或股權價值計算模型，這是金融領域的一個奇特現象。這個現象耐人尋味，值得深思。

不妨再看一個數字例子。

股票D、E、F今年的每股收益都為1元，預計未來可預見時期中（15年左右）年均增長率分別為18%、28%、38%。三家公司風險相當，股權資本的適用貼現率都為12%。

可以判斷，上述信息非常符合現實中投資者所關注的內容，即每股收益大小及其增長潛力以及公司的風險情況。然而，這三只股票收益增長率都超過適用的貼現率，其價值已經無法運用Gordon增長模型來計算，只能使用ZZ增長模型計算。

ZZ增長模型需要每股收益E、增長率g以及要求回收期n三個數據。其中，回收期n可以通過要求收益率即貼現率的倒數得到。在本例中，根據適用貼現率12%，可以得出投資者對三只股票的要求回收期都為：1/12% = 8.33年。

因此，三只股票的價值為：

PD=1+18%8.33-11+18%/18%= 19.48（元），

PE=1+28%8.33-11+28%/28%= 31.19（元），

PF=1+38%8.33-11+38%/38%= 49.55（元）。

從上述計算得出的三只股票價值來看，計算結果對增長率取值適度敏感，而不是過度敏感。而且在增長率取值不受限制的同時，要求回收期取值也不受限制，即模型中n的值可以根據情況取任何整數、小數、分數。

本例的計算說明，ZZ增長模型可以輕松解答Gordon增長模型所解答不了的評估問題。既然如此，一個有趣的問題是，對于Gordon增長模型解答不好的問題，如前面A、B、C股票的例子，ZZ增長模型是否可以給予更好的解答呢？

在股票A、B、C的例子中，明年的每股紅利都為1元，未來長期中年均增長率分別為8%、9%、9.5%，股權資本的適用貼現率都為10%。

首先可以判斷，增長率8%、9%、9.5%不可能是永續增長率，因為根據前面的分析，足夠長時期中的增長率不可能為正數。所以，這里的增長率只能是有限期的增長率，或者說，應該是可預見時期的增長率。假設三家公司的分紅比率保持不變，則這里的增長率也是每股收益在可預見時期的增長率。要由紅利數額得出每股收益數額，需要知道分紅比率。由于本例不是具體公司，沒有另外的信息，作為應用演示，不妨假設三家公司分紅比率與我國A股平均的分紅比率相當，即大致為20%。注意，（1+g）E =明年每股收益=明年每股紅利/分紅比率。另外，同樣，貼現率為10%意味著要求回收期為10年。

將這些變量取值代入ZZ增長模型，可得：

PA=1+8%10-1/20%/8%= 56.19（元），

PB=1+9%10-1/20%/9%= 58.37（元），

PC=1+9.5%10-1/20%/9.5%= 59.49（元）。

A、B、C三只股票的評估值分別為56.19元、58.37元、59.49元，對應于三只股票在增長率上略有差異，評估值也略有差異，再次說明ZZ增長模型對增長率取值的適度敏感特征。而前面應用Gordon增長模型計算的股票價值分別為50元、100元和200元。相比而言，哪個模型的計算更為合理，讀者不難作出明確判斷。

綜上所述，ZZ增長模型可以解決Gordon增長模型解決不了的問題，也可以更好地解決Gordon增長模型解決不好的問題。上述兩個例子已經說明，ZZ增長模型對代表收益與風險的三個變量適度敏感，可以容忍一定的變量取值估計誤差，得出的結論合理、可信，這些都說明模型在應用可行性方面沒有問題。而Gordon增長模型對增長率過度敏感，對增長率估計要求非常準確;而現實中其實搞不清楚模型中的長久或永續增長率究竟是正是負，由此決定了該模型其實沒有應用可行性。

四、Gordon增長模型的改進余地

鑒于應用Gordon增長模型時增長率誤差對股票評估值的過度影響，現實應用中有將股票的未來收益期進行階段劃分，只在最后階段應用Gordon增長模型的嘗試，即所謂的兩階段、三階段模型等，期望以此來改進股票價值的評估。

所謂兩階段和三階段模型并未改變Gordon增長模型，本質上是對Gordon增長模型的限制或削弱，即只留部分未來現金流量用Gordon增長模型來評估其價值，然后加上非Gordon增長模型評估的部分得出股權或股票價值。

當然，兩階段和三階段模型改變不了Gordon增長模型的任何缺點，包括其沒有應用可行性的缺點。因此，兩階段和三階段模型不屬于對Gordon增長模型的改進。與其說是改進，不如說是對Gordon增長模型的否定，或者說是部分否定。也就是說，實踐中兩階段和三階段模型的應用正是對本文前面分析結論的佐證。

進一步，兩階段或三階段模型等嚴格講也不是一個模型，而是多個模型的簡單疊加。經過疊加，未知數的個數顯著增加，理論上講，應用難度應該不小于多個模型難度的加和。既然Gordon增長模型本身沒有應用可行性，而兩階段或多階段模型對此又無能為力，那么，這些多階段模型自然也就沒有應用可行性。

如此看來，關鍵還是Gordon增長模型本身有問題。那么，有沒有可能對Gordon增長模型自身加以改進或修正呢？

在折現計算價值的框架內，必然是未來收益折現加總得出價值。對于股票而言，需要考慮未來多少年的收益呢？由于股權沒有到期期限的特征，人們自然容易傾向于按照無限長時間來理解。即便考慮到公司壽命有限，股票收益期不可能超過公司壽命，但由于公司預期壽命難以估計，加之不同公司預期壽命不同，不太可能在模型中加入一個壽命年數變量，自然會取無限長時間。在無限長時間中，股票的收益都表現為紅利收益，因此，按照預期紅利折現得出股票價值有合理性。同時，又不可能逐年預測紅利或紅利增長率。自然而然，紅利預測采用了初始值和不變即平均增長率兩個指標結合的方式。基于這樣的預測和折現計算價值的思路，經過嚴格的邏輯推導，必然得出Gordon增長模型。

這樣看來，Gordon增長模型是通過折現計算價值的。而長期以來，折現方法是綜合考慮資產的風險和收益計算價值的唯一方法。由此可以理解，為什么Gordon增長模型有致命缺陷甚至根本沒有應用可行性，但卻是長期中廣泛應用的唯一模型。其他模型即便有，往往也是該模型的變型，終難擺脫該模型的致命缺陷。

因此，要解決股票或股權價值評估難題，必須突破折現方法的思路框架。也就是說，股票或股權價值評估面臨的問題不是如何改進Gordon增長模型，而是如何另尋思路、另起爐灶解決問題。然而，不用折現方法，用什么方法呢？似乎脫離折現難以找到計算價值的思路。

可喜的是，這個難題已經由ZZ增長模型予以解決。

五、相對價值評估的缺陷與補救

Gordon增長模型和ZZ增長模型都屬于絕對價值評估的方法。現實中的股票或股權價值評估還有一種常見方法，即相對價值評估。絕對價值評估按照資產的風險和收益特征評估其價值，其最大優點是具有理論合理性，因為價值本來就是由資產的風險和收益決定的。相對價值評估按照相關資產的價格評估某個資產的價值，其最大的優點是簡便易行，因此，在現實的資產價值評估包括股票或股權價值評估中得到廣泛應用。

在股票價值評估領域，相對價值評估具體化為應用評估倍數得出股票價值的方法，常用的有市盈率、市凈率和市銷率三大倍數或比率，分別是股票價格與每股收益、每股賬面凈資產以及每股銷售收入的比值。如果要評估一只股票的價值，先根據其他股票或行業平均得出市盈率、市凈率和市銷率的“合理倍數”，再用被評估公司的每股收益、每股賬面凈資產和每股銷售收入與相應的倍數相乘，即得出股票的價值。

前面提到，Gordon增長模型長期以來幾乎是股票或股權價值評估的唯一模型，這個說法在絕對價值評估范圍內不會有異議，但不強調這個范圍也問題不大。原因之一是相對價值評估可以算一種方法，但不太能算得上是一種模型，其計算價值的過程充其量是可比指標（每股收益等）乘上一個倍數。原因之二是市盈率、市凈率和市銷率倍數取決于什么，似乎過于模糊，現實中除了主觀隨意確定就是按照行業平均值或歷史平均值確定，從而使得相對價值評估缺少科學性和合理性，經不起質疑和推敲，難以與正規方法相提并論。

根據市盈率、市凈率和市銷率的概念可知，相對價值評估是根據其他股票的價格評估某股票的價值，這種做法其實需要一個前提才能成立，即其他股票的價格符合或等于價值。可是，既然其他股票的價格等于價值，為什么待評估股票的價格就不等于價值，需要通過評估計算其價值呢？顯然，這個前提不成立。當然，許多人已經認識到相對價值評估的缺陷，強調不應該簡單應用可比公司當前的市盈率、市凈率和市銷率得出待評估股票的價值，而應該根據行業平均或歷史平均的比率計算待評估股票價值。

可是，如果說一家公司一個時點價格不代表價值，那多家公司多個時點價格的平均數就代表價值嗎？其實，無論是行業平均還是歷史平均，平均價格仍然是價格而不是價值。可想而知，取牛市階段的行業平均比率，或者數據中包含的牛市階段占比大，倍數將會偏高，評估出的某股票價值也會偏高;相反，取熊市階段的行業平均比率，或者數據中包含的熊市階段占比大，評估出的某股票價值則會偏低。由于市場價格不是價值，無論是牛市還是熊市都是如此，基于某種平均的評估比率得出的股票價值也就不是價值。

如果說Gordon增長模型具有理論合理性，但缺少應用可行性，那么，相對價值評估則是依據價格評估價值，缺少理論合理性。也就是說，全世界都依賴的兩大股票價值評估方法，一個沒有應用可行性，另一個沒有理論合理性，而且此外基本沒有另外的方法和模型。無論如何，緊急而重要的問題是，究竟應該如何評估股票或股權的價值？或如何找到既有理論合理性又有應用可行性的模型或方法？這正是本文的主題。

相對價值評估理論上不合理的根本原因是用價格代替價值，評估股票價值時無法排除市場定價偏差的影響。既然如此，在計算市盈率時用待評估股票的價值替換可比股票的價格，就可以解決相對價值評估不合理的缺陷。具體而言，在股票價值模型兩邊都除以每股收益E，即可得出理論市盈率。顯然，理論市盈率有合理性，因為它是基于待評估股票的風險和收益特征計算得到的市盈率，也可稱為無泡沫市盈率。用理論市盈率代替主觀隨意確定的市盈率，或者行業或歷史平均的市盈率，就解決了市盈率方法缺乏理論合理性的問題。

不考慮Gordon增長模型的嚴重缺陷，模型兩邊同除以每股收益E，可以得出基于Gordon增長模型的理論市盈率模型，即：

PE=DE1+Gk-g=x1+gk-g（3）

不妨稱式（3）為Gordon市盈率模型。其中，x = D/E，為分紅比率。這個模型表明，理論市盈率取決于分紅比率x、貼現率k以及增長率g。在分紅比率一定的情況下，理論市盈率取決于公司的風險（k）和增長率（g），而且市盈率與公司增長速度正相關，與公司風險負相關。可以理解，這些特征說明模型有理論合理性。然而，分母的（k-g）說明增長率g還是必須小于貼現率k，而且模型的結果（P/E）對增長率g過度敏感，說明該模型“繼承”了Gordon增長模型的缺點，自然也包括沒有應用可行性的缺點。

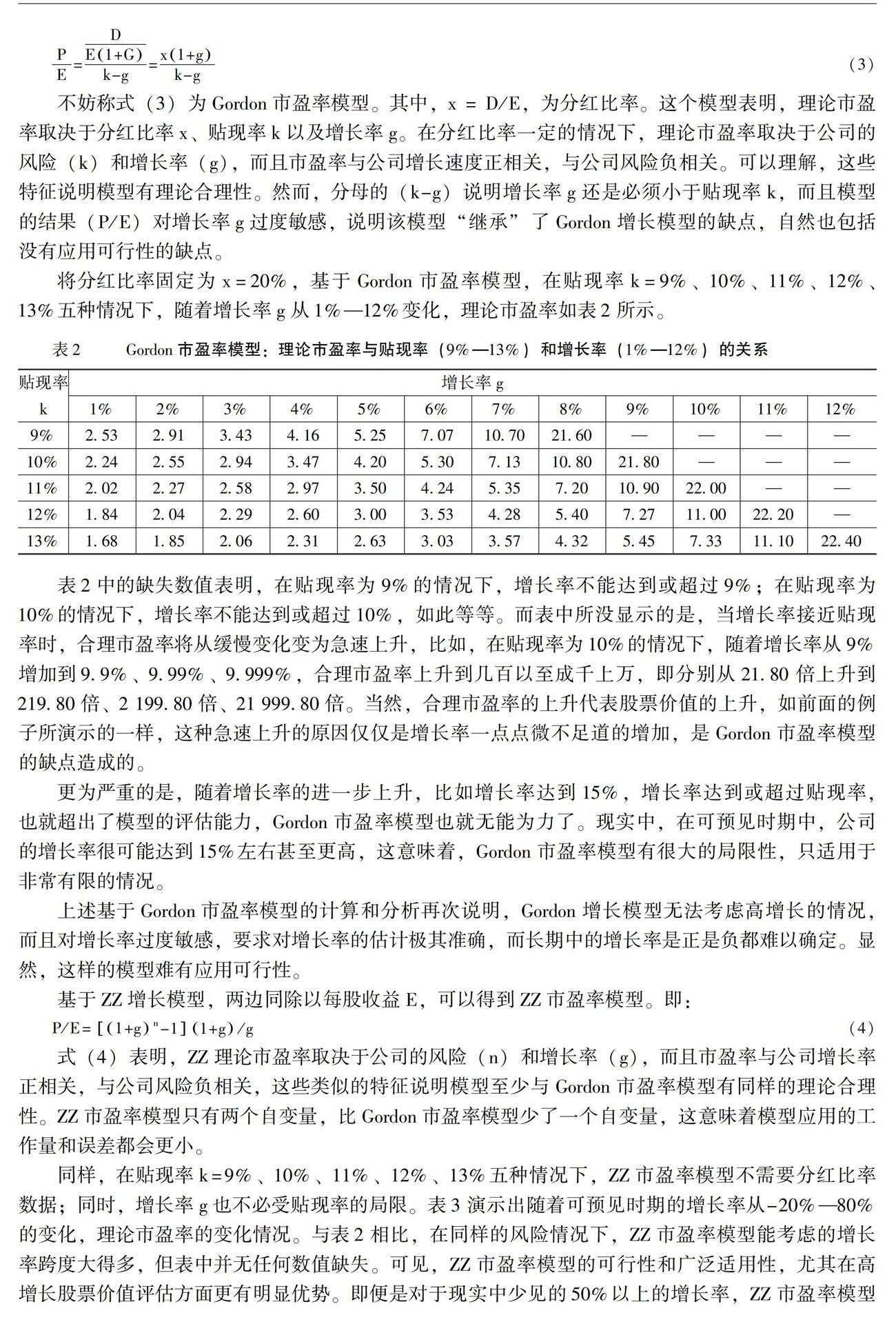
將分紅比率固定為x=20%，基于Gordon市盈率模型，在貼現率k=9%、10%、11%、12%、13%五種情況下，隨著增長率g從1%—12%變化，理論市盈率如表2所示。

表2中的缺失數值表明，在貼現率為9%的情況下，增長率不能達到或超過9%;在貼現率為10%的情況下，增長率不能達到或超過10%，如此等等。而表中所沒顯示的是，當增長率接近貼現率時，合理市盈率將從緩慢變化變為急速上升，比如，在貼現率為10%的情況下，隨著增長率從9%增加到9.9%、9.99%、9.999%，合理市盈率上升到幾百以至成千上萬，即分別從21.80倍上升到219.80倍、2 199.80倍、21 999.80倍。當然，合理市盈率的上升代表股票價值的上升，如前面的例子所演示的一樣，這種急速上升的原因僅僅是增長率一點點微不足道的增加，是Gordon市盈率模型的缺點造成的。

更為嚴重的是，隨著增長率的進一步上升，比如增長率達到15%，增長率達到或超過貼現率，也就超出了模型的評估能力，Gordon市盈率模型也就無能為力了。現實中，在可預見時期中，公司的增長率很可能達到15%左右甚至更高，這意味著，Gordon市盈率模型有很大的局限性，只適用于非常有限的情況。

上述基于Gordon市盈率模型的計算和分析再次說明，Gordon增長模型無法考慮高增長的情況，而且對增長率過度敏感，要求對增長率的估計極其準確，而長期中的增長率是正是負都難以確定。顯然，這樣的模型難有應用可行性。

基于ZZ增長模型，兩邊同除以每股收益E，可以得到ZZ市盈率模型。即：

P/E=1+gn-11+g/g（4）

式（4）表明，ZZ理論市盈率取決于公司的風險（n）和增長率（g），而且市盈率與公司增長率正相關，與公司風險負相關，這些類似的特征說明模型至少與Gordon市盈率模型有同樣的理論合理性。ZZ市盈率模型只有兩個自變量，比Gordon市盈率模型少了一個自變量，這意味著模型應用的工作量和誤差都會更小。

同樣，在貼現率k=9%、10%、11%、12%、13%五種情況下，ZZ市盈率模型不需要分紅比率數據;同時，增長率g也不必受貼現率的局限。表3演示出隨著可預見時期的增長率從-20%—80%的變化，理論市盈率的變化情況。與表2相比，在同樣的風險情況下，ZZ市盈率模型能考慮的增長率跨度大得多，但表中并無任何數值缺失。可見，ZZ市盈率模型的可行性和廣泛適用性，尤其在高增長股票價值評估方面更有明顯優勢。即便是對于現實中少見的50%以上的增長率，ZZ市盈率模型也可以應付自如。注意理解，當增長率為0%時，P/E=n。因此，市場要求收益率為9%、10%、11%、12%、13%情況下，合理的市盈率分別為11.11、10.00、9.09、8.33和7.69倍。

長期以來，股市中主要為傳統行業的股票，人們心目中的合理市盈率范圍為15—30倍左右[13-18]。也就是說，好公司的市盈率可以接近30倍，超過30倍則被看作是高估，這個認知在相對價值評估中有所應用，比如，在主觀隨意確定市盈率的情況下，人們常用的市盈率倍數往往在15—30倍這個范圍。然而，15—30倍市盈率適用于低速或常態增長的公司，并不適用于近些年大量涌現的高速增長的高科技公司和網絡公司。

如果公司在未來一定時期內高速增長，其股票價值應該如何評估？面對這樣的問題，不僅Gordon增長模型無能為力，就連只求簡單方便不求甚解的相對價值評估也無所適從。因為從某種程度上講，相對價值評估屬于基于經驗的評估。既然是基于經驗，當然要靠經驗的長期積累才能獲得有把握的評估。而面對高增長公司，沒有多少人有足夠的經驗。以15—30倍的市盈率經驗值范圍，如何評價動輒幾百倍、上千倍的高科技股票市盈率？

有了ZZ市盈率模型，對合理市盈率的認識就可以超越經驗值范圍。

從表3可以看出，如果公司未來較長時期平均能達到高速增長，幾百倍、上千倍的市盈率都屬于正常，即沒有泡沫。比如，在公司風險情況屬于中等的情況下（貼現率為10%），如果公司可以達到未來十幾年平均增長率為30%、40%、50%、60%、70%、80%左右，則合理的市盈率分別為55.41倍、97.74倍、170.00倍、290.54倍、487.17倍、801.11倍。可以想象，再過幾十年，隨著人們對于高科技高增長公司的見識和經驗的積累，靠主觀確定合適市盈率倍數的能力也會有所提升。但即便如此，主觀確定市盈率顯然也不能達到模型計算的精度。無論何時，靠經驗都只能得出模糊的結論，難以解答精確的定量問題。

在ZZ理論市盈率的基礎上，張志強和俞明軒[8]進一步推導出理論市凈率模型和理論市銷率模型，即：

P/B=1+gn-11+gre/g（5）

P/S=1+gn-11+grs/g（6）

其中，P/B為理論市凈率，re為預計凈資產收益率，即ROE;P/S為理論市銷率，rs為預計銷售利潤率。顯然，ZZ理論市盈率、市凈率和市銷率模型，也都是概念和邏輯嚴謹的封閉解模型，從模型形式到模型中的自變量，都由嚴格而客觀的邏輯推理決定，不是作者自己的主觀選擇，不受作者自己主觀偏好的影響，這意味著這些模型有廣泛而長久的適用性。由ZZ增長模型的特征所決定，這些理論比率模型也都兼有理論合理性和應用可行性，從而可以從根本上全面改變相對價值評估三大比率方法主觀隨意、缺少科學性以及無法適應高科技、高增長股票評估的缺點。

六、結 論

金融是經濟的血脈，股票是金融中最活躍的板塊。股票或股權的并購、上市以及各種交易決定著資金和資源流向、決定著大批公司和行業的格局，也決定著眾多個人的命運。可想而知，每一個這類決策的背后，都有大量的專業人才耗費心血進行分析和計算。在耗費時間精力收集到大量有用信息之后，能夠輸入正確的模型是多么重要！

本文的分析揭示出，作為評估中理論上的主流模型甚至是唯一模型，Gordon增長模型有理論合理性但沒有應用可行性，而實踐中同樣廣泛運用的評估比率方法有應用可行性但沒有理論合理性。運用這兩種評估方法顯然難以得出可信和可靠的評估結論。

經過多方面比較分析發現，ZZ增長模型符合風險與收益決定價值的基本原理，兼有理論合理性和應用可行性，特別是方便評估高增長的股票。不僅如此，基于ZZ增長模型還可以得出市盈率、市凈率和市銷率三大理論比率模型，從而可以改進相對價值評估;不僅可以從根本上提升其理論合理性，而且可以提高其評估能力。

在科技引領經濟、帶動以至決定經濟增長的時代，資本市場迫切需要既有理論合理性又有應用可行性的評估模型，特別是能夠應對高增長特征的模型。可以預計，在這樣一個科技與資本和經濟日益融合和加速發展的時代，缺少科學性和可行性的模型終將退出歷史舞臺，而ZZ增長模型作為真正可以考慮增長的模型，將大有用武之地。

參考文獻：

[1] 楊潔. 科創板開市一周年掃描： 132家企業上市， 總市值逾2.7萬億元 [N]. 中國證券報， 2020-07-21.

[2] Gordon， M. J. Dividends， Earnings， and Stock Prices [J]. The Review of Economics and Statistics， 1959，41（2）： 99-105.

[3] Gordon， M. J. The Savings Investment and Valuation of a Corporation [J]. The Review of Economics and Statistics， 1962，（44）： 37-51.

[4] 師芙琴， 林黎. “兩階段增長”模型應用探析 [J]. 財會通訊（理財版）， 2007，（1）： 26-28.

[5] 高勁. 兩階段增長模型的五種模式——股票定價的股利貼現模型的新思考 [J]. 廣西師范大學學報（哲學社會科學版）， 2007，（5）： 51-55.

[6] 張志強. 高級財務：理論創新與決策應用[M].北京：北京大學出版社，2012.88-115.

[7] 張志強， 趙全海. 確實存在正的永續增長率嗎——關于財務/金融理論的基礎性思考 [J]. 當代財經， 2010，（6）： 48-58.

[8] 張志強， 俞明軒. 理論比率模型與股票價值評估 [J]. 中國資產評估， 2010，（4）： 56-66.

[9] 溫彬， 劉淳， 金洪飛. 宏觀經濟因素對中國行業股票收益率的影響 [J].財貿經濟， 2011，（6）： 51-59.

[10] 馬歡. 我國股票收益率影響因素的實證分析 [J]. 時代金融， 2018，（8）： 31-38.

[11] 王立榮， 李成宇， 洪嘉陽. 我國各行業股票收益率的分布特征 [J]. 當代經濟研究， 2018，（8）： 53-60.

[9] 鄧可斌， 關子桓， 陳彬. 宏觀經濟政策與股市系統性風險——宏微觀混合β估測方法的提出與檢驗 [J]. 經濟研究， 2018， （8）： 68-83.

[10] 張春玲， 姜富偉， 唐國豪. 資本市場收益可預測性研究進展 [J]. 經濟學動態， 2019，（2）： 133-148.

[11] 謝謙， 唐國豪， 羅倩琳. 上市公司綜合盈利水平與股票收益 [J]. 金融研究， 2019，（3）： 189-206.

[11] Fama，E.F.， French，K.R. A Five-Factor Asset Pricing Model [J].Journal of Financial Economics， 2015， 116（1）： 1-22.

[13] Fama，E.F.， French，K.R.International Tests of a Five-factor Asset Pricing Model [J].Journal of Financial Economics， 2017， 123（3） ： 441-463.

[14] Fama，E.F.， French，K.R. Choosing Factors [J]. Journal of Financial Economics， 2018， 128（2） ： 234-252.

[18] Avdisa， E.， Wachter，J.A. Maximum Likelihood Estimation of the Equity Premium [J]. Journal of Financial Economics， 2017，125（3）： 589-609.

[12] Kashyap，R. Solving the Equity Risk Premium Puzzle and Inching Toward a Theory of Everything [J]. Journal of Private Equity Spring， 2018，21（2）： 45-63.

[13] Weber， M. Cash Flow Duration and the Term Structure of Equity Returns [J]. Journal of Financial Economics， 2018， 128（3）： 486-503.

[14] Shi， Z. Time-Varying Ambiguity， Credit Spreads， and the Levered Equity Premium [J]. Journal of Financial Economics， 2019，（134）： 617-646.

[15] Dasilva， A.， Farka，M.， Giannikos，C. Age‐Dependent Increasing Risk Aversion and the Equity Premium Puzzle [J]. Financial Review， 2019，54（2）： 377-412.

[16] Lam， K.， Dong，L.， Yu，B. Value Premium and Technical Analysis： Evidence from the China Stock Market [J]. Economies， 2019， 7（3）： 1-21.

[17] Mehra， R.， Prescott，E.C. The Equity Premium： A Puzzle [J]. Journal of Monetary Economics， 1985，15（2）： 145-61.

[25] Weil， P. The Equity Premium Puzzle and the Risk‐Free Rate Puzzle [J]. Journal of Monetary Economics， 1989，（24）： 401–21.

[26] Kandel， S.， Stambaugh，R.F. Asset Returns and Intertemporal Preferences [J]. Journal of Monetary Economics， 1991，（27）： 39–71.

[27] Fama，E.F. ，French，K.R. Multifactor Explanations of Asset Pricing Anomalies [J]， The Journal of Finance， 1996， 51（1） ： 55-84.

[28] Faugere， C.， Erlach，J.V. The Equity Premium： Explained by GDP Growth and Consistent with Portfolio Insurance [J]. Financial Review， 2006，（41）： 547–64.

[29] Christian，G.， Edward， S.Information and the Equity Premium [J]. Journal of the European Economic Association， 2011，（9）： 871–902.

[18] Lee， E.， Chang， S.K.， Kim，I.M. Equity Premium Over Different Investment Horizons [J]. Empirical Economics， 2015，48（3）： 69-87.

（責任編輯：楊全山）

收稿日期：2021-03-15

作者簡介：

張志強（1965-），男，山東萊州人，副教授，管理學博士，主要從事公司財務與金融研究。E-mail：jinronglilun@126.com