基于學習進階的模型區分
許娟

【摘要】數學模型因為高度抽象,學生往往容易把它們混淆。本文從學習進階的角度為學生提供學習路徑,為學生區分數學模型建立切實可行的行動指南。
【關鍵詞】學習進階? 模型? 活動經驗
學習進階是學習者在學習某一主題的過程中,對于主題內概念的想法與理解程度逐漸加深的發展過程,一般呈現為圍繞核心概念展開的一系列由簡單到復雜、相互關聯的概念序列。
我國數學家徐利治教授認為:“數學模型乃是針對或參照某種事物系統的特征或數量相依關系,采用形式化數學語言,概括地或近似地表述出來的一種數學結構。”數學模型因為高度抽象,學生往往容易把它們混淆。本文從學習進階的角度為學生提供學習路徑,為學生區分數學模型建立切實可行的行動指南。
一、三“階”設計,區分運算規律模型
“階”以學情的把握與分析為重要依據,是一個漸次遞進的過程,學習進階是學習者與知識之間主客體共同作用的結果。對于“乘法結合律和分配律”模型,學生“錯用”“亂用”的情況很嚴重,教師教學時可以根據學生認知的特點,設計三“階”學習任務,引導學生學習,逐步實現基礎性和發展性目標。
1.第一階
我們已經學習了加法、乘法的運算規律,用字母怎么表示?
加法交換律? ? ? ? ? ? ?,加法結合律? ? ? ? ? ? ?,適用于? ? ? ? ? ? 運算;
乘法交換律? ? ? ? ? ? ?,乘法結合律? ? ? ? ? ? ?,適用于? ? ? ? ? ? 運算。
第一階為什么這樣設置?
反思學生的常見錯誤:25×12=25×10×2,沒有凸顯分配律與其他四條運算律的實質性區別。
2.第二階
加法交換律、結合律只適用加法運算,乘法交換律、結合律只適用乘法運算,這四條運算律都是單一運算的規律。教師由此很自然地提出問題:“加法和乘法之間有什么運算規律呢?”讓學生對知識加深印象,不容易弄混概念。
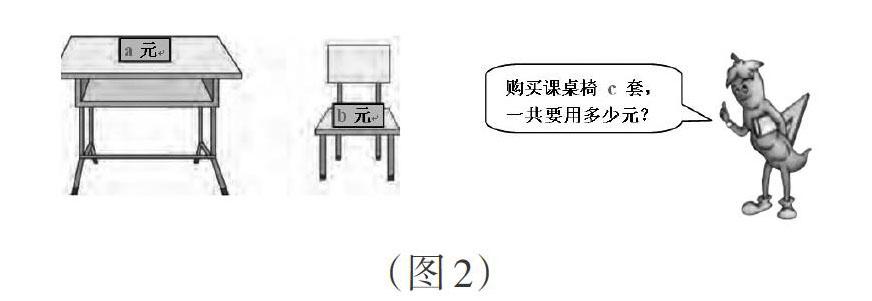
例如,一張桌子50元,一把椅子20元,購買課桌椅3套,一共要用多少元?
學生列式:(50+20)×3=50×3+20×3。
教師提問:為什么這樣算?
實際意義:一套桌椅70元,3套桌椅210元;3張桌子150元,3把椅子60元,一共210元。
算理推導:(50+20)×3=(50+20)+(50+20)+(50++20)=(50+50+50)+(20+20+20)= 50×3+20×3。
3.第三階
把具體的數據換成字母a、b、c(如圖2),總結出乘法分配律:(a+b)×c =a×c+b×c。
三階設計,包含了圖形語言、符號語言、文字語言,如果學生能夠在三種語言之間自主轉換,也就完全理解了乘法分配律。
二、拾“階”而上,區分度量單位模型
1. 一維長度、二維面積單位的區分
將“階”的知識嵌入錯題辨析,不僅有利于教師進行精準的結構性補償教學,而且有利于發展學生的數學學習能力。
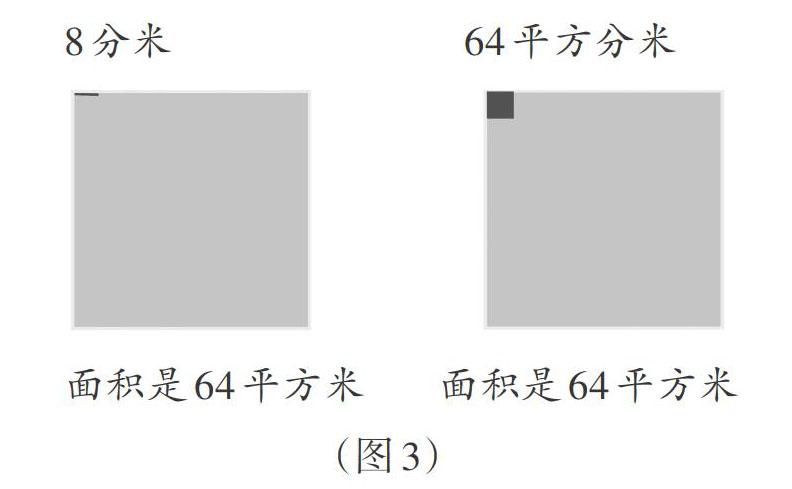
例如:一間會議室面積是64平方米,如果用邊長是8分米的方磚鋪地面,需要多少塊方磚?
有的學生錯誤地列式:64÷8=8(塊)。
根據學生的錯誤,教師需要進行補償性教學:
(1)區分概念,教師比畫1分米、1平方分米、1米、1平方米的大小。
(2)再現性情景應用,根據鋪方磚的場景(如圖3),列式:6400-64-64-64……
(3)生成性情景應用,教師提問:減去多少個64呢?最終列式:6400÷64=100。
8分米? ? ? ? ? ? ? ? ? ? ? ? ? ? 64平方分米
對長度、面積單位模型的區分,教師不僅僅是讓學生復習之前學過的知識,更是為了層層進階,讓學生建立新的學習策略。
2.整數、小數長度單位的區分
著名數學家波利亞曾精辟地指出:“數學有兩個側面,一方面它是歐幾里得式的嚴謹科學,從這個方面看,數學像是一門系統的演繹科學;但另一方面,它是創造過程中的數學,看起來卻像是一門實驗性的歸納科學”,并指出“抽象的道理很重要,但要用一切辦法使他們能看得見摸得著”。
0.6米=6(? ?),要在括號里填合適的單位名稱,學生會在“毫米”“分米”“厘米”三個單位之間猜想。天津的一位教師在上課時,讓學生在尺上標注0.6米,學生給出了3種不同的答案。
如圖(圖4、圖5、圖6):
圖4中,學生認為,有6個“毫米格”,0.6米就是6毫米。圖5中,學生認為,有6個“厘米格”,0.6米就是6厘米。圖6中,學生認為,0.6米是6分米,手指著沒有刻度的米尺,從0.6米(6分米)、0.7米(7分米)、0.8米(8分米)、0.9米(9分米),一直數到1米。前面兩位學生忽然發現:0.6米標在6毫米、6厘米處太小了。學生在數數和比畫的過程中積累了活動經驗。
數學活動經驗是知識、是過程、是經歷,主體性、動態性、活動性是其主要特征。學生在“做數學”的過程中、在“數學化”的過程中、在“數學探究”的過程中,獲得了活動經驗。在“0.6米=6分米”的教學中,活動經驗發揮了關鍵作用,學生從中享受到了學習進階的成功。
(作者單位:江蘇省句容市教師發展中心)

