一種具有動態適應性的狼群算法及其應用

余澤泰 余盟 肖人彬 鐘衛衛 王玉梅

摘要 為了提高狼群算法的適應能力，使其能在復雜環境下具有較高的尋優精度與速度，提出一種具有動態適應性的狼群算法。首先，提出一種動態分群算法，增強狼群算法的全局適應性;其次，定義一種差異度擬熵，構造自適應步長，提高算法在復雜環境下的精度與收斂速度;使用隨機游走環節，增強算法的適應性，縮短計算耗時。在17種測試函數上與其他幾種算法進行對比，顯示所提出算法具有較好的精度與收斂速度。在三維無人機航線規劃問題上驗證了該算法的有效性與實用性。

關 鍵 詞 狼群算法;動態適應性;分群;差異度擬熵

中圖分類號 TP18? ? ?文獻標志碼 A

Dynamical adaptive wolf pack algorithm and its application

YU Zetai， YU Meng， XIAO Renbin， ZHONG Weiwei， WANG Yumei

（Artificial Intelligence and Automation， Huazhong University of Science and Technology， Wuhan， Hubei 430074， China）

Abstract In order to improve the adaptability of the wolf pack algorithm， and provide it with good performance of search accuracy and speed under complex environment， a dynamical adaptive wolf pack algorithm （DAWPA） is proposed. Firstly， a dynamic clustering algorithm is proposed to enhance the global adaptability. Secondly， a difference pseudo entropy is defined to construct self-adaptive variable step-size， which improves the search accuracy and convergence speed. Random scout method is used to enhance the adaptability and shorten the computing time. Then， DAWPA is applied on 17 benchmarks. Compared with several other algorithms， DAWPA has shown better performance on accuracy and speed. Finally， application of DAWPA on 3D UAV route planning problem has demonstrated its validation and utility.

Key words wolf pack algorithm; dynamical adaptability; clustering; difference pseudo entropy

群智能優化算法是通過模擬自然界中生物種群的行為方式，來求解復雜優化問題的智能算法。相比于傳統的優化算法，群智能優化算法在解決一部分NP難問題上展現了良好的效果，得到了大量研究，在解決優化問題上得到了廣泛應用。

國內外學者已經提出了多種群智能算法，如粒子群算法（Particle Swarm Optimization， PSO）和人工蜂群算法（Artificial Bee Colony， ABC）。這兩種算法得到廣泛應用，在優化中展現了獨特的優勢[1]。然而，面對復雜問題時，它們出現了較嚴重的早熟現象[2-3]。

為了解決復雜情況下的尋優問題，在狼群捕獵方式的啟發下，吳虎勝等[4]提出了一種新的群智能優化算法——狼群算法（Wolf Pack Algorithm， WPA），并基于馬爾科夫鏈證明了該算法的收斂性。由于WPA具有較好的全局搜索能力，自提出就引起國內外學者關注，并被應用于生產調度、圖像處理、路徑規劃、云計算等問題[5]，在高維問題上具有較好的收斂與魯棒性[6]。同時，針對一些特殊的問題，一系列衍生的應用算法也被開發出來。例如，應用于0-1背包問題的二進制狼群算法（BWPA）[7];應用于TSP問題的離散狼群算法（DWPA）[8];應用于多目標0-1規劃問題的元胞狼群算法[9];應用于模糊雙層背包問題的改進二進制狼群算法（IBWPA）[10]等。此外，結合BWPA與柔性種群更新策略的柔性二進制狼群算法（FWPA）被應用于解決一系列靜態多維背包問題，展現了優秀的性能[11]。

WPA對高維復雜函數的尋優效果較好，可以有效避免早熟現象。然而，基本狼群算法還存在一些不足。面對問題特征較復雜，如當優化目標為兼具高維、耦合特征、多峰等復雜性質的場景，如具有復雜環境的水下三維路徑規劃問題、高維度多約束的水電站廠內優化運行問題[12-13]，基本狼群算法的適應能力不夠強，較易早熟，因此影響了收斂速度與尋優精度[14]，出現了收斂速度慢、求解精度不夠高和容易陷入局部最優等問題。為了提高其適應性，文獻[15]通過引入精英集策略（Elite Set Strategy）和差分進化改進了WPA的初始解生成方式，提高了面對不同優化問題時的適應能力。文獻[6]給出了基于對立學習的初始解優化方案，提出了對立狼群算法（OWPA），既提高了正常情況下狼群算法的局部搜索能力，又提高了復雜情況下種群分布的多樣性，具有更好的魯棒性。文獻[16]使用Tent混沌映射初始化狼群，在圍攻過程中加入levy飛行方法，提出了一種混沌狼群圍捕算法，提高了算法的實時性。文獻[17]將混沌理論和反向學習結合起來實現狼群算法的優化，通過優化初始解的方式，提高了面對復雜問題時的全局自適應性。文獻[18]基于適應度將狼群分為子群，提出了自適應狼群分組策略，使狼群算法在復雜環境下具有更好的適應能力。針對原始狼群算法游走步長與圍攻步長固定、缺乏局部自適應能力的問題，出現了多種基于迭代次數[19]、歐氏距離[20-21]、適應度函數[22]的自適應步長狼群算法，且得到了較充分的研究。文獻[23]使用基于迭代次數的自適應圍攻步長，將PSO算法中求解當前局部最優的思想引入到游走、召喚行為中，提出一種改進狼群算法，并將其運用于Otsu圖像分割中，提高了分割精度且縮短了分割時間。文獻[24]在游走行為中加入隨機擾動算子，借鑒模擬退火方法改進了圍攻過程，提高了算法的全局搜索能力。文獻[25]在基本狼群算法的基礎上，增加了二次游走與人工狼變異的環節，在應用問題上獲得了較高精度。

本文在以往研究的基礎上，提出一種具有動態適應性的狼群算法（Dynamical Adaptive Wolf Pack Algorithm， DAWPA）。在狼群的群體分工上，通過使用一種動態分群算法，根據環境與狼群分布動態調整子群數量，使算法的全局搜索更充分。在圍攻環節中，定義一種差異度擬熵，構造自適應的圍攻步長。對游走環節，使用隨機游走策略代替貪婪策略，從而增強算法的適應性。使用17種測試函數，通過與其他6種群體智能算法進行對比，顯示DAWPA具有較好的收斂精度與速度。最后，將DAWPA算法應用到復雜三維環境的無人機航路規劃問題上，驗證了該算法的有效性與實用性。

1 基本狼群算法

狼群算法（WPA）通過模擬狼群捕食行為及其獵物分配方式，抽象出游走、召喚、圍攻3種智能行為以及“勝者為王”的頭狼產生規則和“強者生存”的狼群更新機制。其中，游走行為對應于探狼的貪婪搜索，在游走方向中挑選獵物氣味最濃的方向前進。探狼的位置更新規則如下式：

[xpid=xid+sin2π×p/h×stepa]， （1）

式中：[xid]為探狼i在第d維的當前位置; [xpid]為探狼i向第p個方向前進后在第d維所處的位置;h為最大前進方向;[stepa]為游走步長。

召喚行為是頭狼發起召喚，人工狼向頭狼靠近的過程，人工狼的位置更新方式遵從以下公式：

[xi′=xi+stepb?xlead-xi/xlead-xi]， （2）

式中：[xi]為人工狼i更新前的位置;[xlead]為頭狼位置;[stepb]為圍攻步長;[xi′]為人工狼i更新后的位置。當人工狼與頭狼距離小于給定閾值時，人工狼以頭狼位置作為獵物位置，向其發起圍攻。每次人工狼的位置發生變動后，若適應度高于頭狼，位置更新的人工狼將會成為新的頭狼。通過人工狼與頭狼之間的互動，不斷更新狼群的位置，從而逼近最優解。圍攻行為根據下式調整人工狼位置：

[xi′=xi+λ?stepc?xlead-xi]， （3）

式中：[λ]為[-1，1]之間均勻分布的隨機數;[stepc]為人工狼的圍攻步長。

模擬自然界弱肉強食的環境，WPA設置了淘汰弱者的狼群更新機制，并隨機生成新的人工狼進行補充，以保持狼群數量的穩定。

2 具有動態適應性的狼群算法

為了提高基本狼群算法的適應能力，DAWPA首先對狼群群體的分工方式進行調整。WPA采取單一頭狼產生規則，當應用環境復雜時，單頭狼模式難以有效搜索多個局部最優解。文獻[18]采取的分群方法，雖然增強了算法的適應性，但該算法僅根據適應度進行分群，沒有考慮狼群在解空間中的分布情況。為了使子群的劃分合理，除了以適應度的大小挑選子群頭狼外，還需根據頭狼間的距離進行篩選，使分群后子群間距離最大化。此外，還需根據環境不同與狼群分布的變化，動態調整子群劃分，以提高算法的動態適應性。

在基本狼群算法中，圍攻行為的步長是固定值，不具有自適應能力。在局部開發上，自適應步長可以增強算法局部的自適應能力。目前，有基于算法迭代次數與以歐式距離為參數的自適應步長方法。基于迭代次數的自適應步長具有動態的自適應能力，隨著迭代次數的增加，步長逐漸減小。但該方法不具有環境自適應性，對于不同的解空間情況采取的是相同的步長大小，削弱了算法的適應能力。以歐式距離為參數的自適應步長在特征可分時具有環境自適應性，但在實際應用中，問題特征的各個維度之間存在相關性時，歐氏距離就不再適用。

為了增加自適應步長的適用范圍，必須使用一種能處理耦合特征的步長調節參數。圍攻過程反映了頭狼將獵物信息傳遞給人工狼，細化指導其捕獵的過程，可以考慮用熵對頭狼與人工狼之間的信息差進行衡量，隨信息差的減小而逐漸減小圍攻步長。然而，Shannon定義的熵不能衡量序列信息。因此，DAWPA設計了一種差異度擬熵，其具有區分序列的能力。通過對頭狼和人工狼的差異度進行擬熵計算，衡量其信息差，進而構造出自適應步長。

最后，為了增強算法的全局搜索能力，DAWPA對WPA的游走策略進行了調整。WPA的游走環節采取的是貪婪策略，探狼向獵物氣味濃度最高的方向前進。為了增強算法避開局部最優的能力，DAWPA使用隨機游走環節以增強其隨機性，當應用環境的適應度函數計算復雜時，可以有效提高算法的全局搜索能力。

2.1 動態分群策略

在自然界中，狼群具有領域性。在環境復雜的情況下，分布較廣的狼群往往會被環境分割成數個子群。被環境分隔的每個狼群的活動范圍較為固定，且遵循各自頭狼的領導。模擬自然界中狼群的領域性，針對復雜的解空間環境，提出如下的動態分群策略。

Step 1：完成狼群的初始化后，設狼群中共有m只狼，計算m只狼對應的適應度，取適應度最高的個體作為子群1的頭狼。為了獲得子群的頭狼，取適應度前5%的狼個體組成頭狼候選集。除了考慮適應度外，新的子群頭狼應與原來的各個頭狼具有較遠的距離，使各子群對解空間的探索更充分。由于各個頭狼之間距離之和隨頭狼數量增加而增加，因此選取新頭狼的距離閾值應與頭狼數量有關。具體來說，從頭狼候選集中選取滿足的人工狼，將其作為新子群的頭狼。

[i=1udi≥23udmax]， （4）

式中：u為現有子群數;[di] 指當前人工狼與現有的第i個子群頭狼的歐式距離;[dmax]指子群1的頭狼到解空間邊界距離的最大值，代表了解空間中相對大的距離，從而可以將其作為距離閾值。

Step 2：由式（4）可以獲得u個子群頭狼，使用kmeans聚類方法，將m只狼劃分為u個子群。

Step 3：對u個子群的人工狼分別進行游走、召喚、圍攻操作。

Step 4：對Tmax次迭代的狼群算法，則在尋優過程中間隔Tmax/10次迭代完成一次“分裂-合并”的子群動態調整。

a）子群分裂：將每個子群適應度僅次于頭狼的人工狼作為頭狼候選集，選取滿足式（4）的人工狼作為新子群的頭狼。

b）子群合并：對每個子群計算距離[di]，若其不滿足式（4），則將其與距離最近的子群合并。合并的子群頭狼為原有兩個子群中適應度大的頭狼。

Step 5：完成“分裂-合并”操作后，重新使用kmeans算法進行聚類操作。

在簡單問題中，狼群間的適應度與在解空間中的分布差異不大，狼群不會被劃分為多個子群，整個狼群一起進行捕獵。而在復雜問題中，問題的解空間環境往往呈現出高維、多峰的性質，求解過程中可能出現多個接近的局部最優解，動態分群策略將會根據狼群自身的適應度與分布情況，動態地調整子群的數量，各個子群可以同時探索多個局部最優解。基本狼群算法只有單頭狼，所有的人工狼都接受其指導，向唯一的局部最優解方向探索;DAWPA采取的動態分群策略，不固定子群的數量與范圍，隨著實際問題與當前狀態的變化進行不同的分群，使狼群算法具有了動態的適應能力。

2.2 基于差異度擬熵的自適應圍攻行為

設兩頭人工狼的位置向量分別為a， b，則它們的差異度向量定義為：

d={di}={ai-bi}， i=1，…，n.

借鑒文獻[26]定義的擬熵（pseudo entropy），定義一種差異度擬熵如下：

定義1

[PE=-k=1ndkpke1-pk]， （5）

式中， [pk0≤pk≤1] 為k在[dk]中的頻率。式（5）定義的差異度擬熵隨兩個個體之間相對信息差的減小而增大，當兩個個體完全一致，即信息差為0時，差異度擬熵取得最大值為0。

差異度擬熵將差異度向量作為系統，通過衡量差異度的混亂程度，聚合了原個體向量間各個維度的綜合信息，從而可以將其作為自適應步長的控制參數，構建自適應的圍攻行為。

[xi′=xi+λ×stepc×xlead-xi]， （6）

式中：[stepc=21+ePE-1];[λ]為[-1，1]之間的隨機數。使用sigmoid函數可以使步長調節更為平滑，同時將差異度擬熵映射為[0，1]的步長。

通過式（6），以差異度擬熵為參數進行自適應步長控制，可以將頭狼和人工狼各個維度的信息差進行有效聚合，使人工狼更可能找到最優解。由于差異度擬熵統計了差異度向量的元素，反饋的控制參數不易受到特征維度與特征關系的影響，因此在高維、特征存在耦合的情況下精度更高。

2.3 游走環節的隨機化

在基本狼群算法的游走過程中，探狼分別向h個方向游走，選擇氣味最濃的方向前進。這意味著游走過程中需要計算m×h次人工狼的適應度。在實際應用問題中，多次適應度函數的計算使游走環節耗時巨大。游走行為本質上是一種隨機搜索過程，是狼群算法跳出局部最優解的重要環節。由于探狼主要由上一次迭代過程中向頭狼發起圍攻的人工狼組成，距離頭狼較近，選擇適應度最高的方向游走，探狼將繼續靠近頭狼，導致狼群進一步陷入局部最優解。因此，為了使算法跳出局部最優解，設置隨機游走環節，人工狼按照下式更新位置：

[xi′=xi+sin2π×randi1，hh×stepa] （7）

式中，[randi1，h] 指從1到h之間的一個隨機整數。該游走行為代表在h個方向中隨機選取一個方向前進。在隨機游走中，不進行適應度的計算，這意味著在游走過程中不進行頭狼替換的操作，保留原有頭狼進入召喚過程。

隨機游走策略在一段時間內保留了原有頭狼的指導，避免反復更換頭狼而帶來搜索不徹底的問題，使人工狼對解空間的探索更充分，避開了局部最優，因此具有提高全局搜索的適應性的效果。同時也大大減少了適應度計算的耗時，加快了算法的效率。

2.4 綜合效果分析

上節分別介紹了DAWPA所使用的3種技術的作用。在DAWPA的尋優過程中，3種技術之間相互作用，其效果互相影響，彌補了部分缺點，增強了算法效果。所提出技術對算法性能的作用如圖2所示。其中，紅色實線代表正面效應，綠色虛線代表負面效應。

動態分群策略強了算法的全局搜索能力，通過將狼群根據環境劃分為子群，提高了種群分布的多樣性進而增加了覆蓋全局最優解的概率，但其精確度不足。

在進行粗略的全局搜索后，圍攻過程可以掃描鄰近區域，提高算法精度。自適應的圍攻進一步增強了復雜函數環境下的尋優精度。然而，自適應步長的引入增加了計算耗時。

隨機游走環節替代了WPA的貪婪游走，減少了重復計算適應度函數與頭狼更新的過程，避免狼群因過于頻繁地更換頭狼導致搜索不充分。此外，隨機游走環節顯著減少了計算耗時，抵消了自適應圍攻的負面效應。

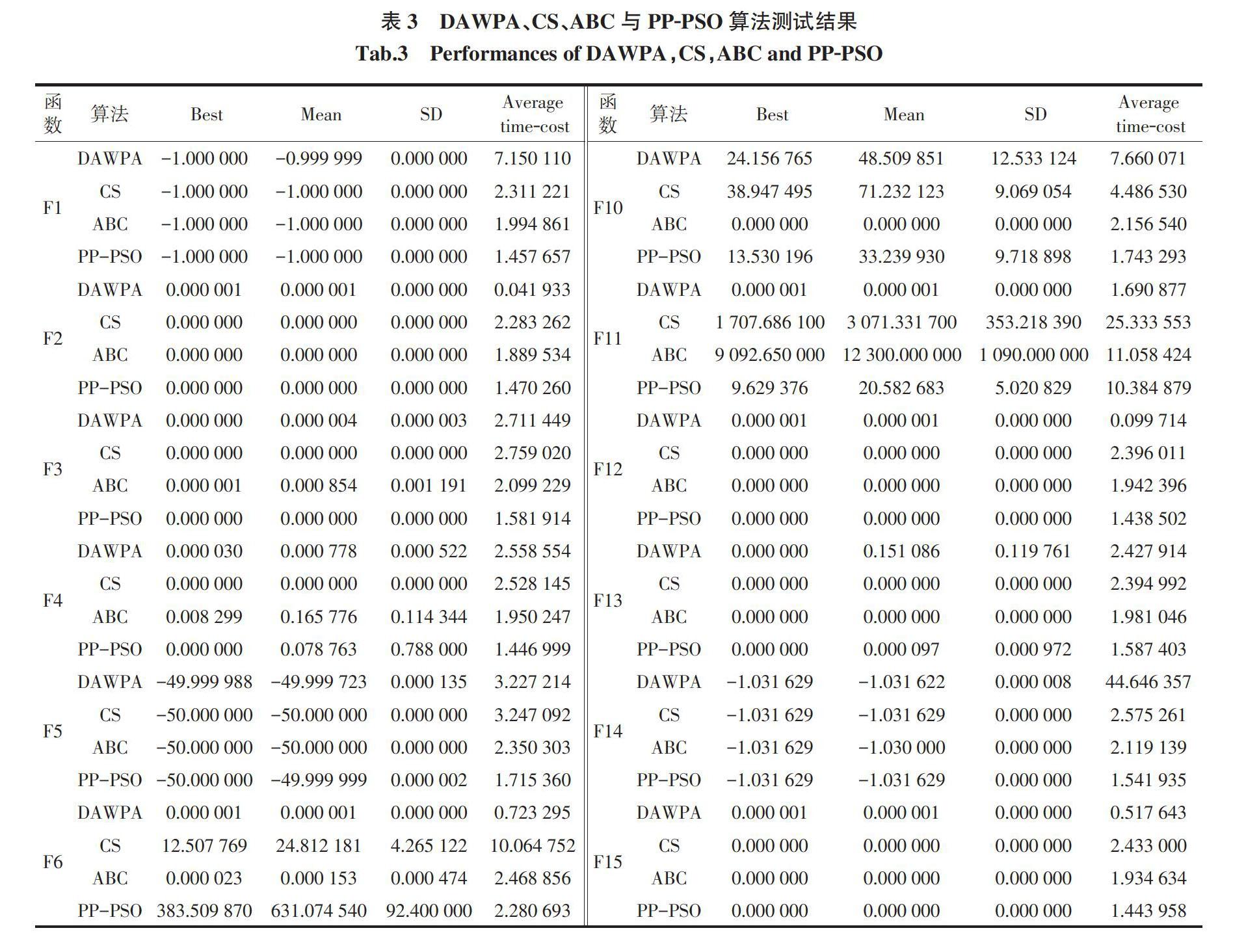
3 DAWPA實現與性能測試

3.1 DAWPA流程

DAWPA的流程圖如圖3所示，其算法步驟如下。

Step 1： 狼群初始化。在解空間中隨機初始化狼群的空間坐標，計算適應度獲得子群1的頭狼。

Step 2： 動態分群環節。根據適應度獲得頭狼候選集，根據式（4）選出子群頭狼，使用kmeans算法分群。

Step 3： 隨機游走環節。根據式（7），令人工狼進行隨機游走，更新其坐標。

Step 4： 各子群的召喚行為。對不同的子群分別進行圍攻，各子群的人工狼分別向各自的頭狼靠近，若人工狼適應度大于頭狼，則其成為新的頭狼。人工狼的位置更新如下式：

[xki′=xki+λbxklead-xki ，]? ? ? ? ? ? ? ? ? ? ? ?（8）

式中：[xki]為第k子群的第i只人工狼; [xki′]為其經過召喚行為后的位置;[λb]為固定召喚步長;[xklead]為第k子群的頭狼。

Step 5： 基于差異度擬熵的自適應圍攻過程。對于每個子群的每只狼，根據式（6）可計算出自適應的圍攻步長，向獵物發起圍攻。

Step 6： 子群種群更新。對種群中適應度差的個體進行淘汰，并產生等量的隨機新個體。

Step 7： 群體的“分裂-合并”行為。在一定的間隔下，在各子群內部挑選頭狼候選，進行分裂;對子群頭狼之間的距離進行計算，根據結果進行合并。

Step 8： 重復過程3-7，直至到達最大迭代次數或算法精度滿足閾值。

為了更好地解釋DAWPA算法流程，提供其偽代碼如下。

Algorithm 1. Pseudo code of DAWPA

Input： the parameters of DAWPA including population size n， step coefficient S， distance determinant coefficient dnear.

Output： the best objective value.

1. Generate initial population of wolves Xi = {xi1， xi2， …， xij， …， xin}

2. Evaluate the fitness of whole population o and select the initial lead wolf Ylead = max{Yi}

3. Clustering method

4. Select wolves with top 5% fitness as leader wolf candidates

5. group_number：=1

6. for candidates i=1;i

7.? if candidate i satisfies Eq. （4） then

8.? ?group_number++

9.? endif

10. end for

11. Generate subgroups using k-means（group_number）

12. Set iteration counter for initial population g：=0

13. while g

14.? for i=1;i

15.? ?Scouting behavior

16.? ?Takes a step towards direction p as in Eq. （7） and update positions of subgroup i

17.? ?Summoning behavior

18.? ?if Yij > Yi_lead then

19.? ? renew lead wolf i and restart the summoning behavior

20.? ?else if Yi ≤ Ylead & dis ≤ dnear then/*dis is the distance between Xlead and Xi*/

21.? ? wolves from subgroup i move to lead wolf i with the moving operator

22.? ?else

23.? ? update their positions as in Eq. （8）

24.? ?endif

25.? ?Besieging behavior

22.? ?if Yi > Ylead then

23.? ? renew the lead wolf

24.? ?else if Yi ≤ Ylead

25.? ? wolves move to the lead wolf with the moving operator

26.? ?else

27.? ? update their positions as in Eq. （6）

28.? ?endif

29.? end for

30.? Split and Merge

31.? for i=1;i

32.? ?if wolf x2 satisfy Eq. （4） then/*x2 refers the wolf that has second highest fitness in subgroup i*/

33.? ? divide group i to 2 subgroups using k-means method

33.? ?endif

34.? end for

35.? for i=1;i

36.? ?if xilead does not satisfy Eq. （4） then

37.? ? subgroup i merges with the nearest subgroup

38.? ?endif

39.? end for

40.? g++

41.? Restart the scouting， summoning and besieging behaviors

42. end while

3.2 測試函數與參數設置

3.2.1 測試函數

參考文獻[27-28]，將DAWPA在17個測試函數上進行10次重復測試。選取的測試函數包含了近年來研究中常用的單峰、多峰、可分、不可分、不同維度等多種類型的函數，以測試算法在多種環境下的表現情況差異[29-32]。

函數與特性如表1所示，U（unimodal）表示單峰函數，M（multimodal）表示多峰函數，S為可分（separable），N為不可分（non-separable）。單峰為在定義域內無局部極值，只有全局最優值的函數;多峰為有多個局部極值的函數，一般的算法較易陷入局部最優值，因此可以用來檢驗算法的全局搜索和避免過早收斂的能力;含有N維自變量且能表示為N個單變量函數之和的函數為可分函數;反之則為不可分函數。

3.2.2 比較算法及參數設置

本文使用人工蜂群算法（ABC）[33]、布谷鳥搜索算法[34]與4種改進狼群算法進行比較。3種狼群算法分別為基于歐氏距離的自適應改進狼群算法（IWPA）[21]、引入趨向游走行為和死亡概率的改進狼群算法（Chemotactic behavior and Death probability WPA， CDWPA）[35]和基于levy飛行的動態狼群算法（Dynamic wolf pack algorithm based on Levy Flight， LDWPA）[36]進行比較。此外，使用一種較新穎的改進PSO算法，prey-predator PSO （PP-PSO）算法進行比較，該算法在CEC2017測試函數集上展現了比其他10種PSO衍生算法更好的性能[37]。為方便讀者閱讀，將結果分兩組進行展示。其中WPA的改進算法（包括DAWPA， IWPA， CDWPA， LDWPA）為一組，其他算法為一組（包括DAWPA， CS， ABC， PP-PSO）。本文統計4個尋優性能指標，分別為最優值（best），平均值（mean），標準差（SD）與平均耗時（average time-cost）。

實驗的最大迭代次數為2 000次，初始種群數目都設為100，精度閾值為1×10-6，即小于1×10-6的精度誤差均可視為0。各算法參數見表2.測試環境為i7-6500U CPU @ 2.50GHz 2.59GHz， Matlab R2018a。測試結果見表3和表4。

3.3 結果分析

本節將從算法精度（包含3.3.2節統計分析）、速度-穩定性能與收斂速度比較三方面，對表3、表4的結果進行分析。

為了方便讀者理解，下面對性能指標的含義進行簡要介紹。“Best”為尋優全程中算法取得的最接近標準值的結果。“Mean”為尋優過程中，所有迭代的平均結果。“SD”為計算結果的標準差，其代表了算法的穩定性能。“average time-cost”為每次尋優（2 000次迭代）的平均耗時。

3.3.1 算法精度分析

表3、表4中的最優值與平均值反映了算法的尋優精度。從低維、可分、單峰的函數，如F1-5的結果來看，DAWPA的尋優精度與其他算法的結果接近。對于低維、不可分、多峰函數，例如F8-9，DAWPA的算法精度與CS， ABC， PP-PSO， CDWPA， LDWPA算法接近，而IWPA則相對較低。對于高維、可分、單峰函數，包括F6-7，DAWPA，ABC和IWPA算法比CS算法略有優勢，同時精度遠高于PP-PSO算法與LDWPA算法。對高維、可分、多峰函數，如F11，4種WPA改進算法具有明顯優勢，顯示其避免陷入局部最優的能力比其他算法強，且DAWPA算法精度優于其他3種WPA改進算法。CS， ABC和PP-PSO算法的優化基于適應度，采取貪婪策略進行更新。但當面對多峰函數時，單純依賴適應度的更新機制極易陷入局部最優解，因此其算法精度不佳。而WPA改進算法采用了游走-召喚-圍攻的做法，由可變的頭狼對其他人工狼進行指導，對全局信息與頭狼附近的局部信息都進行了探索，因此在多峰高維問題上精度較好。相對于其他WPA改進算法，DAWPA加入了分群策略，將解空間中被多個峰分隔的子群進行適當的分群，分別由各自的頭狼召喚、圍攻，同時有間隔的進行子群的合并-分裂，使多個較優的解空間領域得到充分探索，獲得了最好的算法精度。

此外，對多峰不可分的高維函數，如F16-17，其反映了算法對不可分的維度信息的處理能力。計算結果的比較表明，DAWPA的算法精度高于WPA改進算法且遠高于PP-PSO、ABC和CS算法。這證明采用差異度擬熵的自適應圍攻環節對不可分的維度信息處理能力更強，提高了算法的精度。

3.3.2 統計分析

3.3.1節中的分析顯示DAWPA相對于其他算法在復雜函數尋優上具有更好的性能。為了進行進一步的統計分析，本節采取無參數Friedman test分析復雜函數上的平均精度，以測試DAWPA相對其他算法的精度優勢是否顯著[38]。算法平均精度為算法平均結果與標準值的差值的絕對值。原假設認為DAWPA與比較的算法的性能無顯著差異，當p值小于0.05時拒絕原假設且置信度為95%。

為了應用F-test，首先選取多個復雜函數，并將其劃分為兩類。將函數維數大于等于30且小于等于100的函數劃分為中等維數函數（Mid-dimensional），將函數維數高于100的劃分為高維函數（High-dimensional）。函數的劃分如表5所示。

將表3、表4中的平均結果（mean）與標準值的差值的絕對值作為精度指標。借鑒文獻[39]，對每個算法分別計算中等維度函數與高維函數的精度指標的平均值（mean）與中位數（median）。

基于該平均值與中位數，使用Matlab進行F-test，計算p值為0.02<0.05，即可以以95%的置信度拒絕原假設，顯示DAWPA算法對其他算法的精度優勢具有顯著性。指標及計算結果如表6所示。

3.3.3 速度-穩定性能分析

表3、表4中的標準差與耗時分別體現了算法的穩定性和快速性。對于智能算法而言，其速度-穩定性能之間的平衡對算法的應用影響巨大，因此對這兩個指標同時進行分析。由于各個函數復雜程度不同，不同函數的尋優標準差之間存在數量級的差異。為了直觀展示DAWPA相對于其他算法的尋優標準差的情況，使用對數標準差比，即DAWPA的標準差與其他6種算法標準差的比值的對數作為特征，與算法耗時一起展示。對于標準差比值分母為0的情況，若分子也為0，將比值標為1;若分子大于0，將比值標為10 000，則取對數后為4。結果如圖4a）和4b）所示。

在穩定性方面，對于低維、單峰函數， DAWPA的穩定性相對于ABC算法、CS算法較差，與CDWPA和LDWPA互有優劣但較為接近，好于IWPA算法。對于高維、多峰尤其是不可分的復雜函數，如F11、F16、F17，比值曲線出現了明顯的下三角，說明DAWPA在復雜函數上的穩定性顯著好于其他算法，不易受到干擾。在7種算法中，對于高維的復雜函數，DAWPA擁有最好的穩定性。這是因為這5種算法本質上都屬于隨機搜索算法，而當搜索進入到局部最優解時，其他算法基于貪婪的更新策略都容易陷入局部最優，盡管都加入了一定概率的跳出局部最優的操作，但算法穩定性仍然會受到明顯的影響。而DAWPA使用了分群的策略，多個子群同時探索，有更大概率求得全局最優值，算法穩定性得到了提高。從計算耗時上看，DAWPA在低維函數上計算耗時較大，但在高維函數上顯著縮短了耗時，與其他WPA改進算法相比，具有明顯優勢。一方面這是由于分群策略的使用加快了算法求得全局最優解的速度，抵消了計算耗時，另一方面是因為隨機游走環節，相對于WPA的其他改進算法的游走環節減少了適應度函數的計算，因此大幅度減少了計算耗時。

3.3.4 算法收斂情況分析

速度-穩定性能分析顯示，與非WPA改進算法相比，DAWPA具有更好的穩定性，但計算耗時較多。本節通過對收斂過程進行分析，確定耗時較多的原因。由于CDWPA與LDWPA算法的耗時較大，該分析僅涵蓋DAWPA， CS， ABC， IWPA， PP-PSO5種算法。

將尋優誤差隨迭代次數的變化繪制成收斂曲線，選擇一系列高維函數，包括F6， F7， F11，與F17，繪制5種算法在不同函數上的收斂曲線，如圖5。

以高維、不可分、多峰函數F17為例，5種算法的收斂曲線如圖6所示。在100代左右，IWPA算法就基本收斂，其精度停留在1×10-4級別，顯示其可能陷入了局部最優。250代左右，DAWPA算法到達全局最優，達到了更高的尋優精度。2 000代后，ABC與CS算法仍然未能收斂到全局最優解。PP-PSO算法在尋優初期快速下降，但很快陷入局部最優解。

圖5所示其他收斂曲線也顯示DAWPA在速度與精度上具有優勢。IWPA的收斂速度與DAWPA接近，但精確度較差。ABC算法與DAWPA算法在F16上達到了接近的精度，但在F11， F17上性能較差。

分析結果說明，在復雜函數上，DAWPA基于游走-召喚-智能圍攻的尋優過程，相對于PP-PSO、ABC算法和CS算法，能更好地對解空間進行搜索，在尋優能力上有明顯優勢。在多峰不可分函數上，與IWPA的對比證明，DAWPA基于差異度擬熵的智能圍攻過程，對不可分的函數特征有更高的尋優精度。

綜上所述，DAWPA在高維不可分多峰函數上，用一定的計算耗時，換取了明顯的尋優精度、穩定性的提升。在圍攻過程中，DAWPA的動態分群過程和差異度擬熵的計算量大于其他改進WPA算法，花費了較多時間，因此在簡單函數上整體耗時較長;但在如F17等復雜函數上耗時明顯縮短。原因是DAWPA通過動態分群，減小了陷入局部最優的可能;隨機游走環節減少了適應度函數計算的大量耗時;使用差異度擬熵，對頭狼和人工狼的相似度進行了更合適的度量，提高尋優精度的同時，在更少的迭代次數內收斂到最優值，抵消了計算的耗時。測試結果證明，DAWPA算法具有更強的適應能力，不易陷入局部最優解。同時，動態分群與隨機游走環節加快了算法收斂到全局最優值的速度，較PP-PSO、ABC算法、CS算法和其他改進WPA算法有明顯的優勢。

4 DAWPA的實際應用

復雜地形三維航路規劃是指在復雜三維地形環境下，無人機自主規劃一條航線躲避障礙物，同時盡可能減少航程。相比于二維航路規劃，三維情況下搜索空間過大，快速拓展隨機樹[40]、A*算法[41]等傳統二維航路規劃算法的計算時間過長。基于模擬流體流動的思想，文獻[42]提出了基于擾動流體動態系統（IFDS）的三維航路規劃方法，該方法具有光滑的航路特性和快速性，但產生的流線存在局部陷阱或可能停留于駐點。為了解決流線缺陷，文獻[43]提出了改進擾動流體動態系統算法（IIFDS）。在IIFDS算法中，需要對反應系數進行優化，以產生最優航路。多種群智能優化算法在對反應系數進行尋優時，尋優效果隨維度增長而下降，且容易陷入局部最優解[42]。為了驗證DAWPA具有的動態適應性，本文將DAWPA應用于無人機航路規劃，對復雜三維地形下IIFDS算法的反應系數組進行尋優，規劃出較優航線。IIFDS模型參見文獻[42]。

4.1 復雜地形下的三維航路規劃

在IIFDS模型中，排斥反應系數[ρ]、切向反應系數[σ]與切向方向系數[θ]的選取影響了最終航線的方向、形狀與長度。本文使用DAWPA，對其進行優化以獲得較優航線。首先定義適應度函數J。考慮航路長度代價[J1]與障礙物威脅代價[J2]。

[J=μ1J1+μ2J2，]

式中，[μ1，μ2∈0，1]為代價權重系數，有[μ1+μ2=1]。

其次，對于狼群的初始化，設定參數范圍[ρ∈0.1，30、σ∈0.1，30、θ∈-π，π]， 初始化狼群規模N，則[Xi=ρ1，σ1，θ1，...，ρK，σK，θK，i=1，2，...，N]，維度D=3K。

基于3.1節的算法流程，設定規劃空間為[10×10×3]，隨機產生10個不同類型的障礙物，如圖7所示。障礙物高度不一，可以測試算法權衡左右繞行或拉升避障的能力;有單峰障礙物，也有兩個障礙物疊加的多峰障礙，更加貼近實際地形，也增加了難度。

對圖7的地形，設定無人機起點為（0，0，0），終點為（10，10，0.5）。為了無人機的安全，設置代價權重系數[0.3，0.7]，代表較高的避障權重。使用DAWPA、CS算法、ABC算法、PP-PSO算法、IWPA算法、CDWPA算法與LDWPA算法進行比較，設置種群規模N=100，最大迭代次數t=100，進行50次重復實驗，并選取其中適應度最好的航線結果進行比較。

將使用6種算法所得到的航路按照第3節的分組方式分兩組繪制，如圖8a）、圖b）、圖8c）和圖8d），對應的路徑信息如表7所示。對于不可行路徑，其代價記為-。

DAWPA、CS、IWPA和LDWPA算法生成的航線都能在復雜三維地形中避開障礙物到達終點，但ABC、PP-PSO與CDWPA算法生成的路徑未能避開部分障礙物，說明這3種算法未能找到合適的排斥反應系數和切向反應系數。在7種算法生成的路徑中，DAWPA生成的路徑的長度代價與避障代價均小于其他算法，路徑也較為平滑，更加適用于無人機的飛行。

在復雜三維地形下的航路規劃問題中，待優化個體為針對各個障礙物的排斥反應系數、切向反應系數和切向方向系數。由于可能的航線不止一條，該問題有著多峰函數性質。因此，DAWPA的動態分群策略有助于同時探索多條較優路徑，從而更快地找到最優路徑。另外，對于一條航路，避開不同障礙物的角度不是完全獨立的，例如，航線穿過兩個障礙物之間時，對其中一個障礙物避障角度過大會導致無人機進入到另一個障礙物中，引起避障代價的提高。在航線規劃中，各個維度之間存在一定的聯系，優化目標具有不可分函數的特性。DAWPA的優勢在于，使用差異度擬熵對所有維度信息進行統計，因此對不可分函數的局部信息有更強的感知能力。綜上所述，對于航路規劃問題，DAWPA擁有更好的優化效果。

5 結論

本文針對基本狼群算法缺乏適應性的問題，提出了一種具有動態適應性的狼群算法DAWPA，以提高狼群算法在實際應用中的表現。

通過引入動態分群策略，種群的分布可以根據優化環境進行動態調整;使用差異度擬熵改進的圍攻過程提高了復雜環境下的尋優精度;隨機游走環節增強了全局適應性，并減少了計算耗時，從而抵消了前兩個技術帶來的較高的時間代價。在測試函數集上與其他6種算法比較的仿真實驗體現了DAWPA在搜索全局最優與快速收斂上的能力。此外，在三維無人機路徑規劃問題上，DAWPA展現了比其他6種算法更好的優化性能，獲得的飛行路徑航程更短且能良好避障，具有實用性。

本文定義了一種差異度擬熵，具有度量耦合函數特征的相似度與序列信息的能力，拓展了自適應步長算法，理論上對優化目標具有不可分特性的相似性度量具有通用性，可以將其引入其他需要不可分函數相似性度量的智能算法中。另外，本文提出的動態分群策略提供了一種改進的初始解生成方法。由于采取了動態分群的策略，DAWPA在復雜函數上較強的處理能力，可以應用于其他復雜結構問題的尋優，如多水下自主航行器的動態任務分配問題等。下一步可以考慮針對具體問題，進一步優化分群策略，使其適用于更多應用場景。

參考文獻：

[1]? ? GUPTA A，SRIVASTAVA S. Comparative analysis of ant colony and particle swarm optimization algorithms for distance optimization[J]. Procedia Computer Science，2020，173：245-253.

[2]? ? ALFI A，MODARES H. System identification and control using adaptive particle swarm optimization[J]. Applied Mathematical Modelling，2011，35（3）：1210-1221.

[3]? ? SQUILLERO G，TONDA A. Divergence of character and premature convergence：a survey of methodologies for promoting diversity in evolutionary optimization[J]. Information Sciences，2016，329：782-799.

[4]? ? 吳虎勝，張鳳鳴，吳廬山. 一種新的群體智能算法：狼群算法[J]. 系統工程與電子技術，2013，35（11）：2430-2438.

[5]? ? 劉聰，費煒，胡勝. 狼群算法的研究與應用綜述[J]. 科學技術與工程，2020，20（9）：3378-3386.

[6]? ? LI H，WU H S. An oppositional wolf pack algorithm for Parameter identification of the chaotic systems[J]. Optik，2016，127（20）：9853-9864.

[7]? ? 吳虎勝，張鳳鳴，戰仁軍，等. 求解0-1背包問題的二進制狼群算法[J]. 系統工程與電子技術，2014，36（8）：1660-1667.

[8]? ? 吳虎勝，張鳳鳴，李浩，等. 求解TSP問題的離散狼群算法[J]. 控制與決策，2015，30（10）：1861-1867.

[9]? ? 馬龍，盧才武，顧清華，等. 多目標0-1規劃問題的元胞狼群優化算法研究[J]. 運籌與管理，2018，27（3）：17-24.

[10]? WU H S，XUE J J，XIAO R B，et al. Uncertain bilevel knapsack problem based on an improved binary wolf pack algorithm[J]. Frontiers of Information Technology & Electronic Engineering，2020，21（9）：1356-1368.

[11]? WU H S，XIAO R B. Flexible wolf pack algorithm for dynamic multidimensional knapsack problems[J]. Research，2020，2020（11）：1-13.

[12]? ZHANG L Y，ZHANG L，LIU S，et al. Three-dimensional underwater path planning based on modified wolf pack algorithm[J]. IEEE Access，2017，5：22783-22795.

[13]? 李勵，賴喜德，陳小明. 基于改進狼群算法的水電站廠內優化運行研究[J]. 水電能源科學，2019，37（6）：164-168.

[14]? CHEN Y B，MEI Y S，YU J Q，et al. Three-dimensional unmanned aerial vehicle path planning using modified wolf pack search algorithm[J]. Neurocomputing，2017，266：445-457.

[15]? CHEN X Y，TANG C J，WANG J，et al. Improved wolf pack algorithm based on differential evolution elite set[J]. IEICE Transactions on Information and Systems，2018，E101. D（7）：1946-1949.

[16]? 周璟. 混沌狼群圍捕算法的車間機器人導航路徑規劃[J]. 機械設計與制造，2020（1）：251-255.

[17]? 惠曉濱，郭慶，吳娉娉，等. 一種改進的狼群算法[J]. 控制與決策，2017，32（7）：1163-1172.

[18]? 張強，王梅. 自適應分組差分變異狼群優化算法[J]. 華東師范大學學報（自然科學版），2017（3）：78-86.

[19]? ZHU Y，JIANG W L，KONG X D，et al. A chaos wolf optimization algorithm with self-adaptive variable step-size[J]. AIP Advances，2017，7（10）：105024.

[20]? 王盈祥，陳民鈾，程庭莉，等. 基于差分進化的改進狼群算法研究[J]. 計算機應用研究，2019，36（8）：2305-2310.

[21]? 郭立婷. 基于自適應和變游走方向的改進狼群算法[J]. 浙江大學學報（理學版），2018，45（3）：284-293.

[22]? 顏學龍，汪斌斌. 自適應狼群算法優化ELM的模擬電路故障診斷[J]. 計算機工程與科學，2019，41（2）：246-252.

[23]? 曹爽，安建成. 改進狼群優化算法的Otsu圖像分割法[J]. 微電子學與計算機，2017，34（10）：16-21.

[24]? 張舉世. 改進的狼群優化二維Otsu閾值分割算法[J]. 電力學報，2020，35（1）：40-45.

[25]? 李靖宇，王磊，江克貴，等. 基于改進狼群算法的概率積分法模型參數反演方法[J]. 采礦與巖層控制工程學報，2021，3（1）：79-86.

[26]? LI C，MA H，ZHOU Y，et al. Similarity analysis of DNA sequences based on the weighted pseudo-entropy[J]. Journal of Computational Chemistry，2011，32（4）：675-680.

[27]? 薛俊杰，王瑛，李浩，等. 一種狼群智能算法及收斂性分析[J]. 控制與決策，2016，31（12）：2131-2139.

[28]? WU H S，ZHANG F M. Wolf pack algorithm for unconstrained global optimization[J]. Mathematical Problems in Engineering，2014，2014：1-17.

[29]? MOAZZENI A R，KHAMEHCHI E. Rain optimization algorithm （ROA）：a new metaheuristic method for drilling optimization solutions[J]. Journal of Petroleum Science and Engineering，2020，195：107512.

[30]? JAIN L，KATARYA R，SACHDEVA S. Opinion leader detection using whale optimization algorithm in online social network[J]. Expert Systems With Applications，2020，142：113016.

[31]? NAIK A，SATAPATHY S C，ABRAHAM A. Modified Social Group Optimization—a meta-heuristic algorithm to solve short-term hydrothermal scheduling[J]. Applied Soft Computing，2020，95：106524.

[32]? CHOU J S，NGUYEN N M. FBI inspired meta-optimization[J]. Applied Soft Computing，2020，93：106339.

[33]? KARABOGA D，BASTURK B. A powerful and efficient algorithm for numerical function optimization：artificial bee colony （ABC） algorithm[J]. Journal of Global Optimization，2007，39（3）：459-471.

[34]? CUEVAS E，REYNA-ORTA A. A cuckoo search algorithm for multimodal optimization[J]. The Scientific World Journal，2014，2014：497514.

[35]? 鮮思東，李堂金. 基于改進狼群算法的模糊時間序列預測模型[J]. 控制理論與應用，2020，37（7）：1637-1643.

[36]? 韓忠華，劉約翰，李曼，等. 改進狼群算法求解模具在模臺上組合分配問題[J]. 系統仿真學報，2021，33（1）：127-140.

[37]? ZHANG H R，YUAN M，LIANG Y T，et al. A novel particle swarm optimization based on prey-predator relationship[J]. Applied Soft Computing，2018，68：202-218.

[38]? DEMSAR J. Statistical comparisons of classifiers over multiple data sets[J]. Journal of Machine Learning Research，2006，7：1-30.

[39]? TANWEER M R，SURESH S，SUNDARARAJAN N. Self regulating particle swarm optimization algorithm[J]. Information Sciences，2015，294：182-202.

[40]? ZUCKER M，KUFFNER J，BRANICKY M. Multipartite RRTs for rapid replanning in dynamic environments[C]//Proceedings 2007 IEEE International Conference on Robotics and Automation. April 10-14，2007，Rome，Italy. IEEE，2007：1603-1609.

[41]? YANG H I，ZHAO Y J. Trajectory planning for autonomous aerospace vehicles amid known obstacles and conflicts[J]. Journal of Guidance，Control，and Dynamics，2004，27（6）：997-1008.

[42]? WANG H L，LYU W T，YAO P，et al. Three-dimensional path planning for unmanned aerial vehicle based on interfered fluid dynamical system[J]. Chinese Journal of Aeronautics，2015，28（1）：229-239.

[43]? 姚鵬，王宏倫. 基于改進流體擾動算法與灰狼優化的無人機三維航路規劃[J]. 控制與決策，2016，31（4）：701-708.