基于重要性采樣的純方位定位算法

薛昌成，駱吉安，申屠晗

(杭州電子科技大學自動化學院，浙江 杭州 310018)

0 引 言

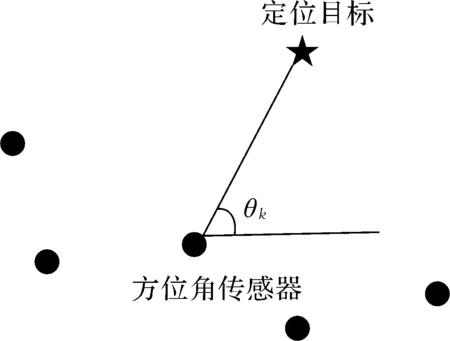
圖1 純方位角目標定位

純方位角定位在目標跟蹤、監視、導航及通信等領域應用廣泛[1]。到達角度(Angle of Arrival，AOA)定位方法通過測量空間分散傳感器相對于目標的方位角來獲得目標位置的估計值，由于角度測量與待估計目標位置是反正切函數關系，真實角度與目標位置是非線性映射的函數[2]。在加性測量噪聲假設條件下，需要用統計信號處理的方法進行位置參數估計。文獻[3]采用偽線性估計(Pseudo-Linear Estimator, PLE)解決純方位角定位問題，PLE算法易于實現，且復雜度較低，但隨著測量次數的增加，偏差并不會消失。在高斯測量噪聲假設條件下，極大似然估計(Maximum Likelihood Estimation, MLE)算法[4-5]實質是一個非凸的非線性最小二乘優化問題，需要采用梯度下降方法進行迭代求解。相比于PLE算法，在傳感器個數增加或者測量次數增加時，MLE算法的估算性能越來越接近克拉美羅下界(Cramer-Rao Lower Bound, CRLB)。但該算法對初始條件敏感，且在觀測數據數量不足或傳感器與目標之間存在非視距等條件下容易發散，導致難以獲得全局近似解[5]。本文使用蒙特卡洛重要性采樣(Monte Carlo Importance Sampling, MCIS)算法來得到純方位角定位問題的近似全局解。應用Pincus定理[6]得到全局解的多維積分形式，并使用蒙特卡洛重要性采樣算法來對其進行近似計算[7]，在引入提議分布后，采用PLE作為初始值，有效計算出目標位置。

1 問題描述

1.1 系統模型

純方位角目標定位問題如圖1所示。假設N個方位角傳感器位置靜止且已知，rk=[rx,k,ry,k]T表示第k個傳感器位置，θk表示第k個傳感器與目標位置的真實方位角。純方位角目標定位原理是在某一時刻中，從有噪聲的方位角和傳感器位置中確定真實的目標位置t=[tx,ty]T。圖1中，方位角、傳感器位置與目標位置之間的關系如下：

(1)

假設方位角測量值受到獨立的零均值高斯噪聲的影響，可以寫為：

(2)

1.2 最大似然估計

方位角測量值的似然函數為：

(3)

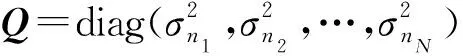
(4)

1.3 偽線性估計

將方位角測量方程線性化[3]，第k個傳感器測量方程如下：

akt=bk+ηk

(5)

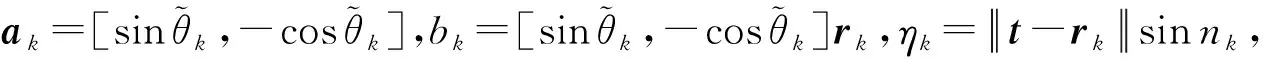
At=b+η

(6)

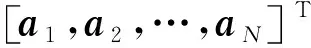
(7)

2 基于蒙特卡洛重要性采樣定位算法

最大似然估計不僅需要采用梯度下降方法進行迭代計算，而且對初始條件敏感，在觀測數據數量不足或傳感器與目標之間存在非視距等條件下容易發散，難以獲得全局解。所以，本文采用蒙特卡洛重要性采樣算法獲得極大似然函數的近似全局解。

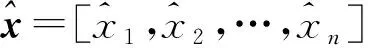
(8)

式中，λ是一個趨于無窮大的常數。根據Pincus定理，得到式(4)的全局解：

(9)

定義函數g(t)為：

(10)

g(t)作為概率密度函數，具有概率密度函數的所有性質，將目標位置t看作隨機向量，將式(9)寫為：

例文(16)中，‘(餅干)’和‘(飲料)’的受事賓語沒有提及，因此對于句子意思而言就產生了歧義現象。如果改為‘’，這樣的句子意思就是‘老師給了我兩個餅干，和兩瓶飲料。’本句話就不存在歧義現象。但文章若是‘’的話，受事賓語是‘我們’，這時本句話就可以解釋為以下三種含義。

(11)

式(11)中的積分難以計算，但可以用蒙特卡洛重要性采樣算法對其進行近似計算。蒙特卡洛重要性采樣算法就是從一定的概率分布中獲取大量樣本，用于計算函數在樣本概率分布上的期望。假設概率密度函數g(x)的隨機向量為x，則x的期望為：

(12)

積分項xg(x)一般都比較復雜，難以用解析的方法求解，但可以從g(x)中采樣得到近似解[8]，若xi(i=1,2,…,N)是從g(x)采樣得到的樣本，則x的期望可以用平均值近似表示為：

(13)

由式(13)計算得到的平均值是對式(12)計算得到的期望的無偏估計，根據大數定理，當N足夠大時，兩者結果非常接近，這樣就把一個復雜的積分問題轉化為一個簡單的求平均值的問題。在實際應用中，實際概率分布g(t)比較復雜，不易直接從實際概率分布進行采樣，可以引入與實際概率分布g(t)的定義域相同的概率分布q(t)，稱為提議分布，使得：

(14)

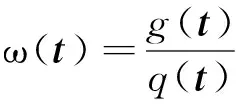
(15)

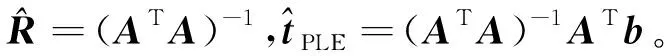
(16)

(17)

不需要計算式(10)的分母，因為它是一個常數，并且在式(16)的計算過程中會約分消除。但是，g(t)的分子是指數的，可能產生很小的值，為了解決這一問題，使用ω′(tm)替換ω(tm)，寫為：

(18)

計算權重時，如何選擇λ的值是一個問題。通過式(8)可以得知，當λ→∞時，全局解達到最優，但在實際應用中，可以將λ設置為足夠大的值[10]。

3 仿真結果及分析

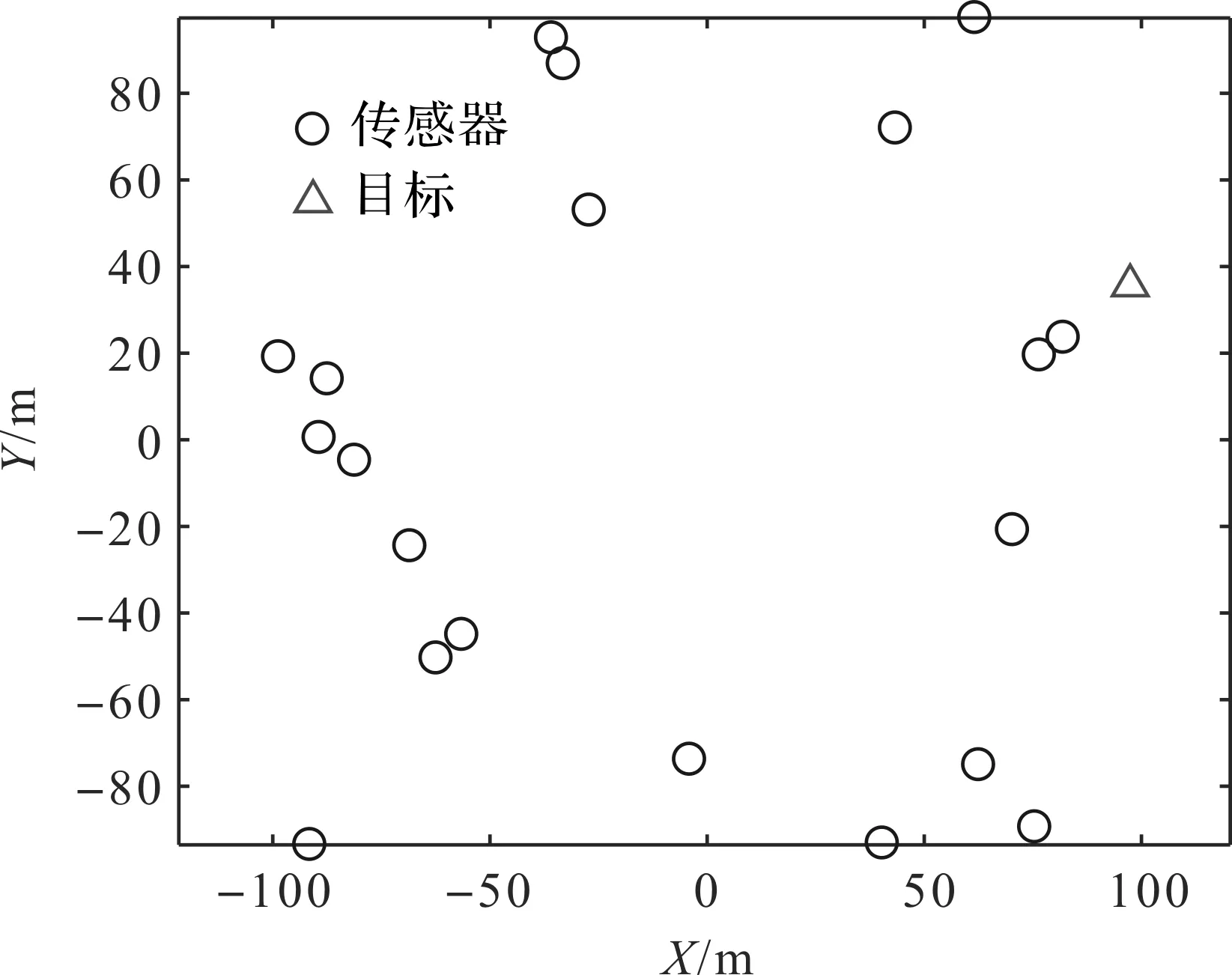
圖2 傳感器與目標位置

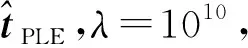
3.1 噪聲標準差對算法性能的影響

實驗場景如圖2所示，目標真實位置和20個方位角傳感器位置隨機分布，傳感器的測量角度受到零均值獨立同分布的高斯噪聲影響，噪聲標準差從π/180增加到8π/180，即1°～8°。

不同方位角噪聲標準差的情況下，PLE，MLE，MCIS和CRLB的RMSE如圖3所示。從圖3可以看出，隨著噪聲標準差的增加，PLE算法的RMSE與CRLB之間的差距越來越大，而MLE和MCIS的RMSE曲線始終與CRLB幾乎重合。PLE，MLE和MCIS的偏差如圖4所示。從圖4可以看出，MLE和MCIS的偏差幾乎相同且很小，而PLE算法的偏差隨著噪聲標準差增加而增加。綜上，MCIS算法和MLE算法在該場景中可以保證良好的性能，而PLE算法性能下降明顯。該場景隨機產生的目標位置及傳感器也保證了MCIS算法具有良好的魯棒性。

圖3 不同噪聲標準差下的RMSE

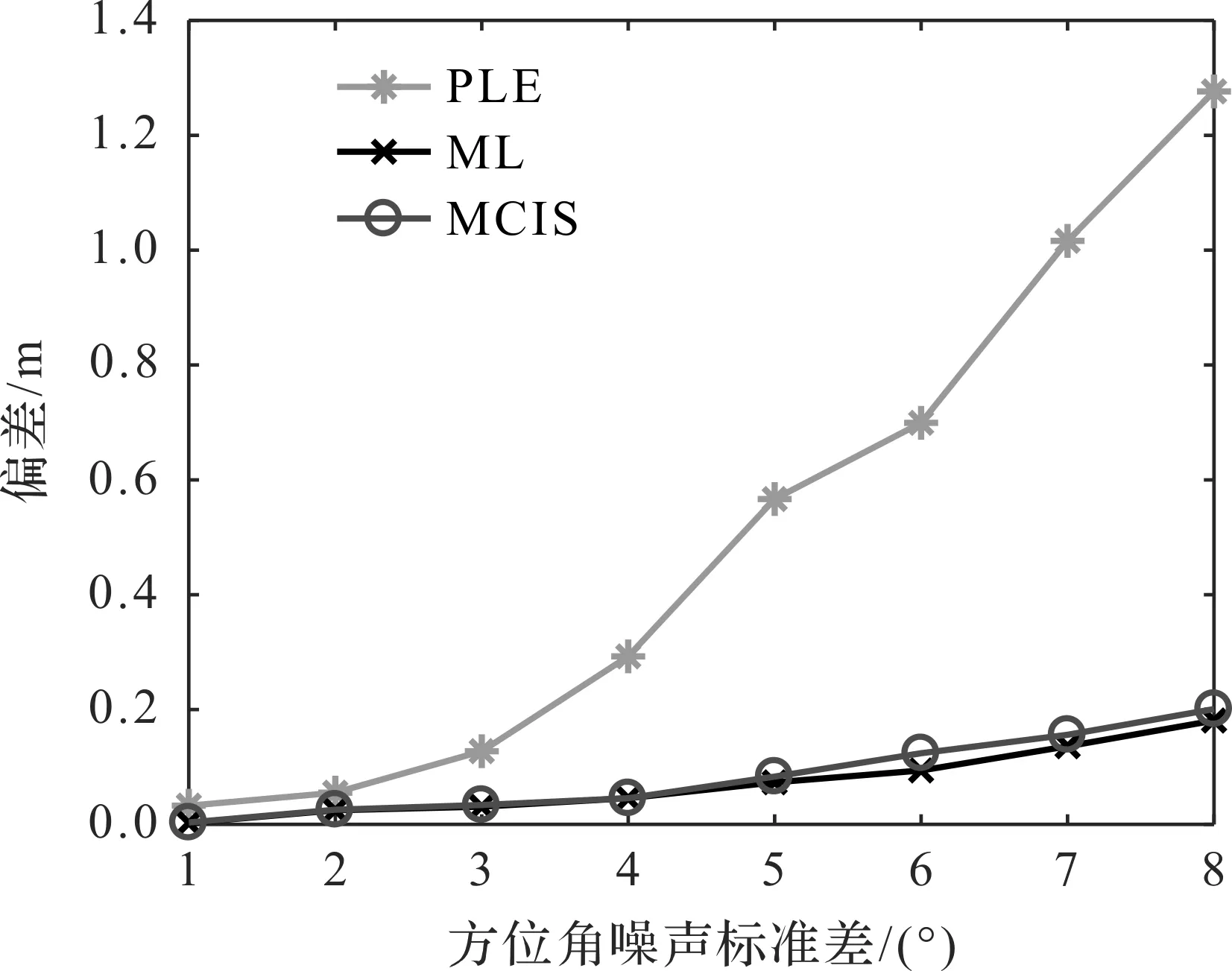
圖4 不同噪聲標準差下的偏差

3.2 傳感器整體到目標距離對算法性能的影響

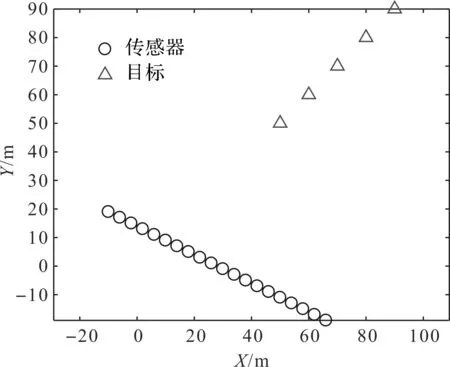
圖5 傳感器及不同目標位置

實驗場景如圖5所示，20個方位角傳感器線性排列，傳感器測量值受到的高斯噪聲標準差為4°，在線性排列的傳感器的右上方設置5個不同的目標位置，坐標分別為[50,50],[60,60],[70,70],[80,80],[90,90]。傳感器到目標位置不同距離的情況下，PLE，MLE，MCIS和CRLB的RMSE如圖6所示。從圖6可以看出，當傳感器到目標位置的距離不斷增加時，MLE和MCIS的RMSE與CRLB非常接近，而PLE算法的RMSE越來越大。PLE，MLE和MCIS的偏差如圖7所示，PLE算法偏差隨著距離的增加而增加，而MLE和MCIS的偏差很小且幾乎相同。綜上，MCIS算法一直保持著和MLE算法相同的性能，達到預期結果，PLE算法性能依舊不理想。

圖6 不同目標位置下的RMSE

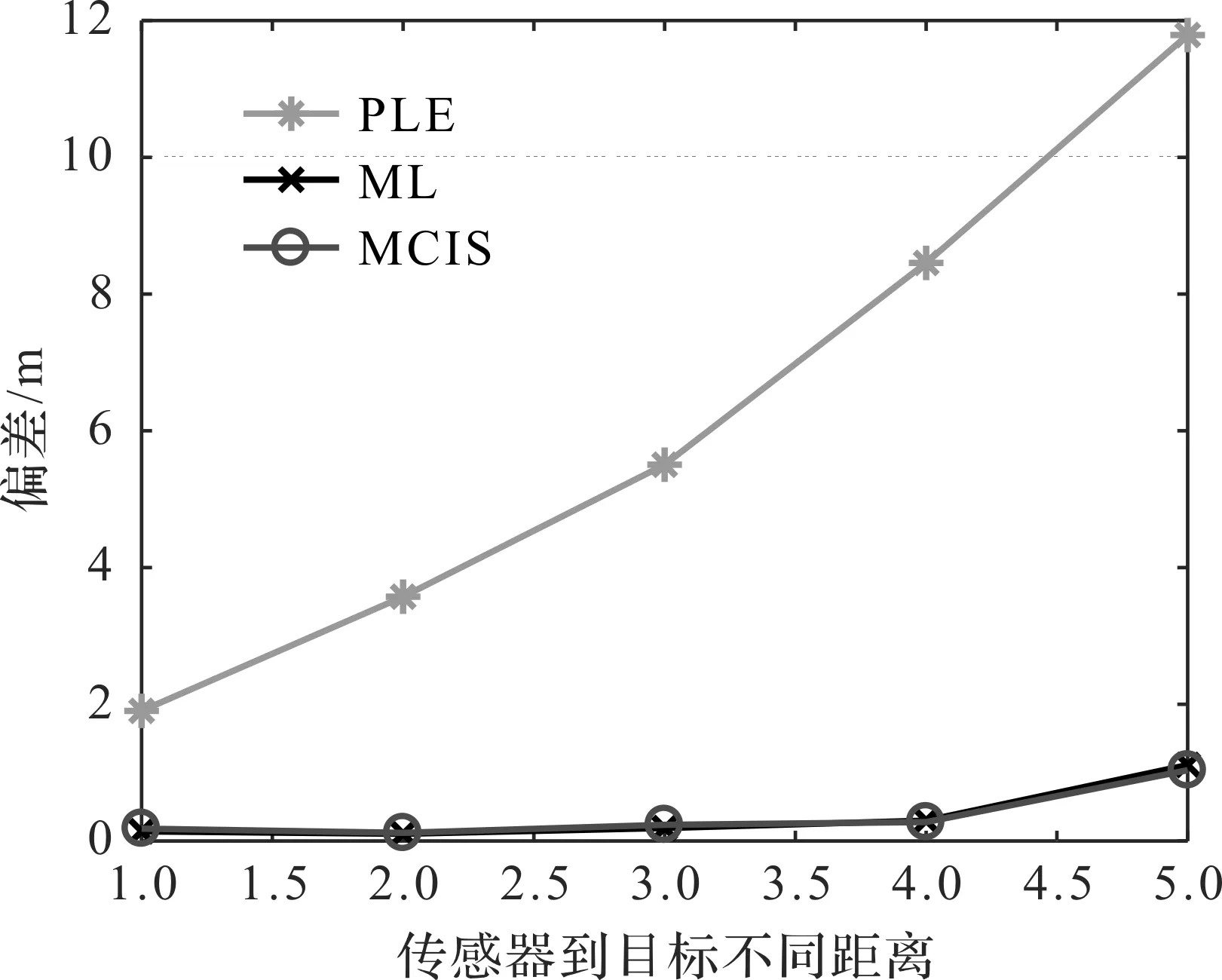
圖7 不同目標位置下的偏差

3.3 傳感器數量對算法性能的影響

為了驗證傳感器數量對算法性能的影響，傳感器位置如圖2隨機排列，數量從12個依次增加到28個，每次增加4個傳感器，傳感器測量值受到的高斯噪聲標準差為4°，目標位置設定為[60,60]。在不同數量傳感器的情況下，PLE，MLE，MCIS和CRLB的RMSE如圖8所示，當傳感器數量不斷增加時，MLE和MCIS的RMSE不斷減小，同樣也很接近CRLB，PLE的RMSE并沒有隨著量測數據的增加而減小。PLE，MLE和MCIS的偏差如圖9所示，PLE算法的偏差隨著傳感器數量不斷增加并沒有減小，而MLE和MCIS的偏差隨著傳感器數量增加而減小。綜上，在增加傳感器的情況下，MCIS和MLE的性能得到了明顯改善，并且這兩種算法性能幾乎相同，而PLE算法改善不明顯。

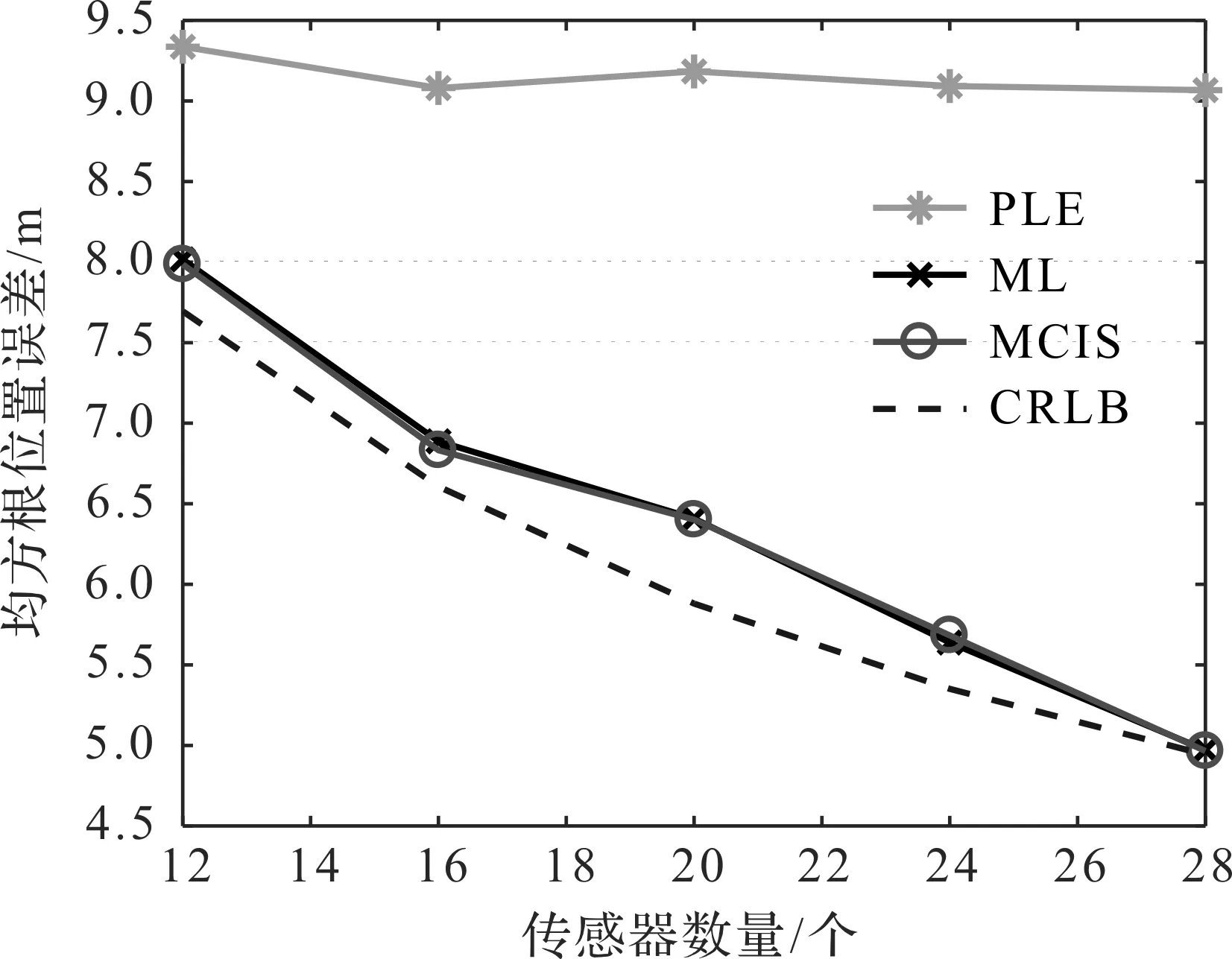
圖8 不同傳感器數量下的RMSE

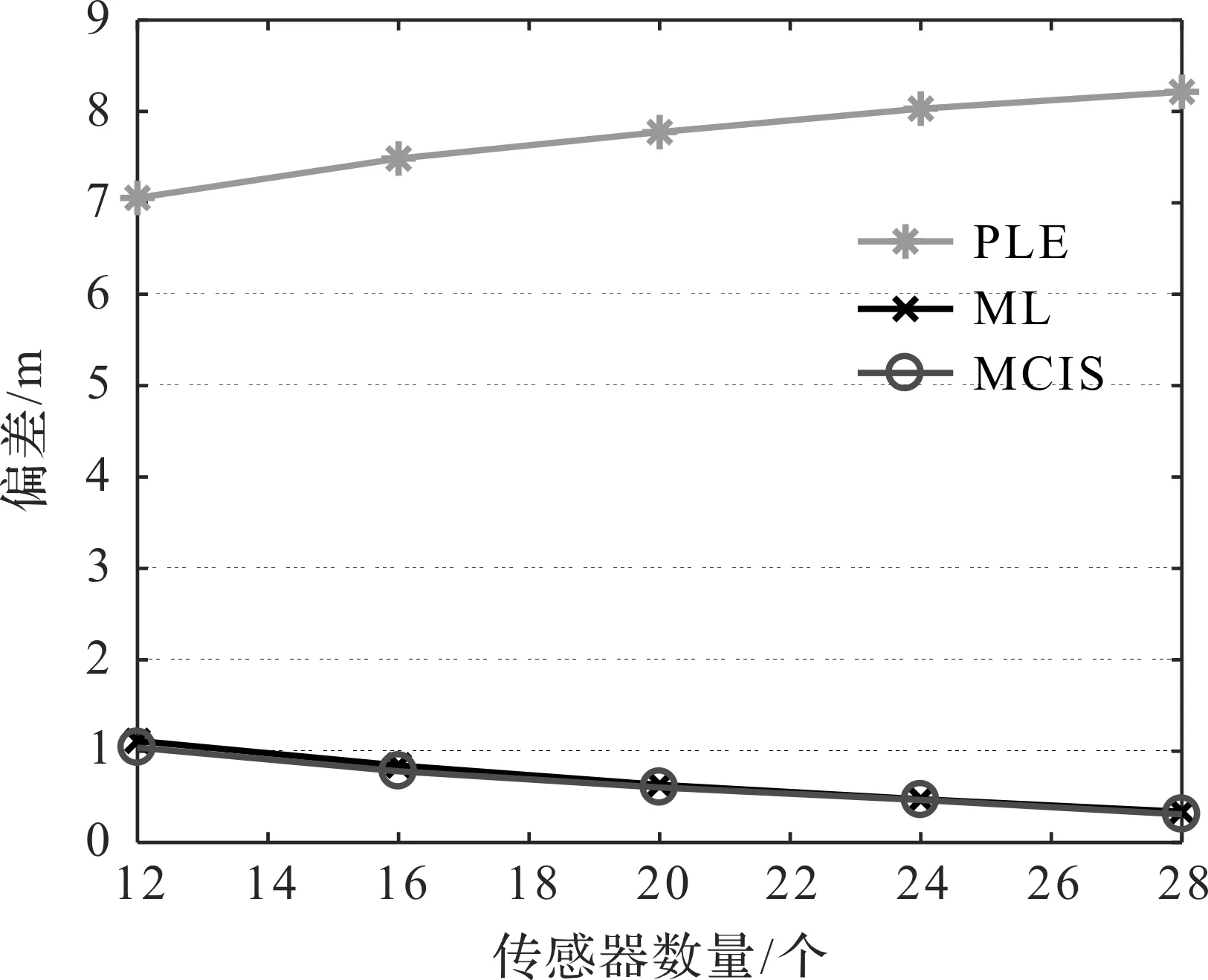
圖9 不同傳感器數量下的偏差

4 結束語

本文提出一種基于蒙特卡洛重要性采樣的純方位定位算法。算法不需要使用迭代方法計算，其性能與MLE算法相同，進一步提高了定位算法的可靠性，具有適用性廣，容易實現等優點。但是，算法僅適用于高斯噪聲環境，下一步將在Alpha穩定分布噪聲環境下展開進一步研究。