運用分類整合思想 提升數學素養品質

山東 楊長智

分類與整合思想是指面對比較復雜問題時，無法通過統一或者整體研究解決，需要把研究對象按照一定的標準進行分類并逐類進行討論，再把每一類的結論綜合，使問題得到解決.其實就是把問題“分而治之、各個擊破、綜合歸納”.

分類與整合思想解題的一般步驟:(1)根據研究需要確定分類標準；各類之間要做到“不重不漏”；(2)逐類逐級進行討論；(3)綜合概括、歸納得出最后結論.本文以2020年高考題為例，剖析在高考中如何考查分類與整合思想，在教學過程中如何分析，提升學生核心素養.

例1:(2020·全國卷Ⅰ文·16)數列{an}滿足an+2+(-1)nan=3n-1，前16項和為540，則a1=________.

教師用PPT展示題目，并讓學生回答.

學生1:需要對n進行討論，分n是奇數和偶數兩種情況.

教師:令S16=S奇+S偶=(a1+a3+a5+…+a15)+(a2+a4+a6+…+a16).

學生1:當n為偶數時，S偶=(a2+a4)+(a6+a8)+(a10+a12)+(a14+a16)，恰好是n取2，6，10，14的情況；當n為奇數時，需要累加分別把a3，a5，…，a15,用a1來表示.

教師:好，根據這種思路我們就得到解題方法一(展示PPT).

解法一:分類討論，逐項突破

當n為奇數時，

a3-a1=2,a5-a3=8,a7-a5=14,a9-a7=20,a11-a9=26,a13-a11=32,a15-a13=38,

分別累加得

a3-a1=2,a5-a1=10,a7-a1=24,a9-a1=44,a11-a1=70,a13-a1=102,a15-a1=140，

即a3=a1+2,a5=a1+10,a7=a1+24,a9=a1+44,a11=a1+70,a13=a1+102,a15=a1+140，

上面各項相加得

a3+a5+a7+a9+a11+a13+a15=7a1+392，

所以S奇=8a1+392,

而S偶=(a4+a2)+(a8+a6)+(a12+a10)+(a16+a14)=5+17+29+41=92，

S16=S奇+S偶=8a1+392+92=8a1+484=540.

所以a1=7.

教師:對于項數不太多時，我們可以把每一個奇數項用a1表示，但項數較多時，這種方法就不可取了，那我們還有沒有其他思路呢？

學生2:我們對n為奇、偶數進行分類討論，看能不能得出奇數項、偶數項的遞推關系，由奇數項遞推公式將奇數項用a1表示，由偶數項遞推公式得出偶數項的和.

教師:很好，根據這種思路，我們求出奇數項時a2k+1與a1的關系(展示PPT).

解法二:分類討論，遞推突破

an+2+(-1)nan=3n-1，

當n為奇數時，an+2-an=3n-1，即

a3-a1=3×1-1，a5-a3=3×3-1，a7-a5=3×5-1，a2k+1-a2k-1=3×(2k-1)-1，

各式相加，得

a2k+1-a1=3×(1+3+5+…+2k-1)-k

=3k2-k，

所以a2k+1=a1+(3k2-k)(k∈N*).

當n為偶數時，an+2+an=3n-1，則

a4+a2=3×2-1=5，a8+a6=3×6-1=17，

a12+a10=3×10-1=29，a16+a14=3×14-1=41.

設數列{an}的前n項和為Sn，

解得a1=7.

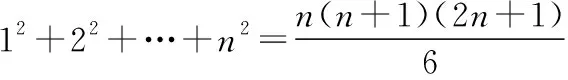
評析:題干中展示的是an+2,an的關系，即數列中間隔項之間的關系，也就是奇數項，偶數項之間的關系；(-1)n的出現提示當n分別為奇數和偶數時有不同的規律，需分類討論；在平常的數列問題中，數列中的奇數項和偶數項分別呈現不同的規律，研究的方法一般是分類討論再綜合處理.本題給的做題線索和思路比較明顯，但計算稍顯煩瑣，學生如果能夠耐心，解決此問題就會比較容易.本題考查邏輯推理、數學抽象、數學運算核心素養.

( )

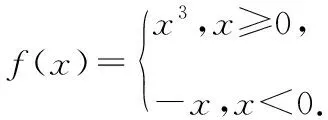
教師:此題f(x)是分段函數，g(x)是f(x)與絕對值函數的組合，如何確定分類標準？

學生3:分段函數的分類標準是x=0，絕對值的分類標準是如何去掉絕對值符號.

教師:絕對值符號如何去掉？

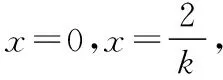
教師:很好，根據學生3的描述，我們可以把g(x)的表達式表示出來，首先是對k進行討論.這樣我們就得到了第一種解題思路.

解法一:利用零點的定義，考查必備知識

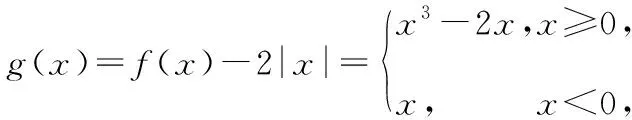
當x<0時，g(x)=x，無零點；

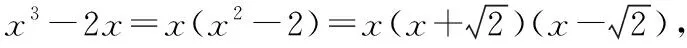
所以當k=0時，g(x)只有兩個零點，不符合題意；

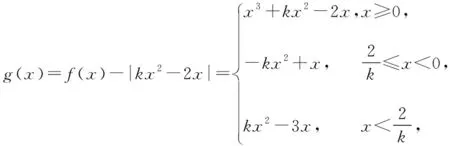
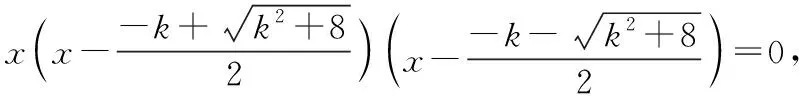
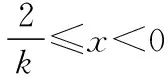
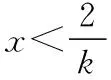
所以當k<0時，g(x)有四個零點，

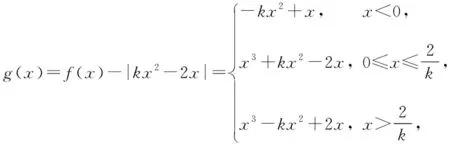
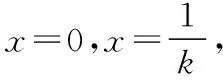
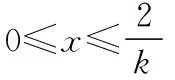
x3+kx2-2x=0,即x(x2+kx-2)=0.

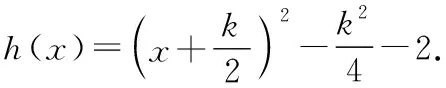
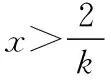
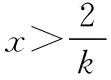
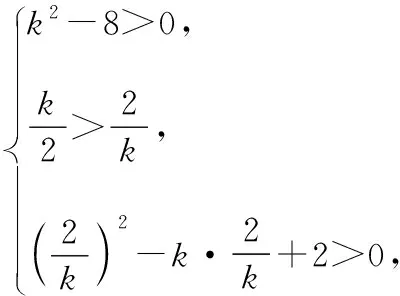
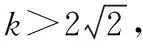
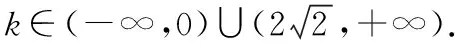
教師:第一種思路是利用零點的定義解決問題，同學們還有沒有其他思路？

學生4:令h(x)=|kx2-2x|，若函數g(x)=f(x)-|kx2-2x|恰有4個零點，只需y1=f(x),y2=h(x)圖象有四個交點.

教師:很好，根據這種思路，我們就把零點問題轉化成兩個函數圖象的交點問題，這里用到了化歸與轉化、數形結合的思想.

解法二:對零點的考查，轉化為兩個函數圖象交點個數

①當k=0時，h(x)=2|x|，

從圖1中可以看出，當x<0時，無交點；當x≥0時，有兩個交點，

所以當k=0時，g(x)有兩個零點.

圖1

②當k<0時，

由圖2可知當x≤0時，y1=f(x),y2=h(x)有三個交點，

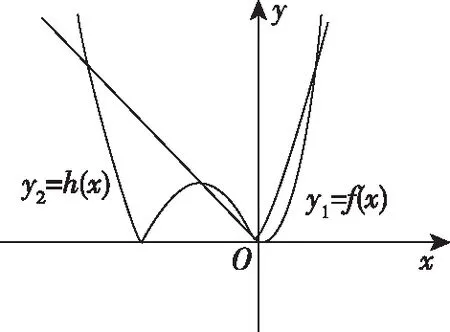
圖2

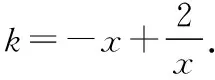
圖3

③當k>0時，如圖4，

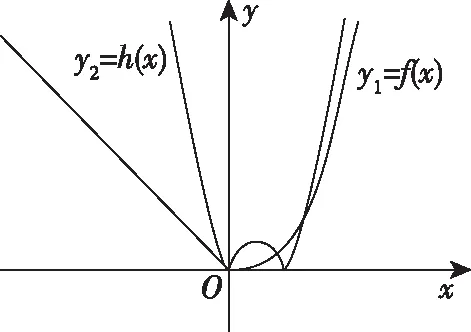
圖4

當x<0時，y1=-x,y2=kx2-2x，由-x=kx2-2x，得kx=1矛盾；

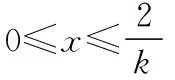
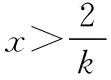
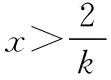
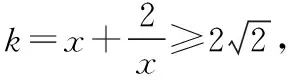
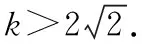
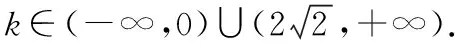
教師:除了上面的思路，同學們還有沒有更簡便的方法呢？

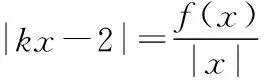
解法三:利用特殊點，將題目進行化歸轉化

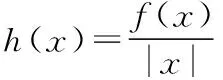
圖5

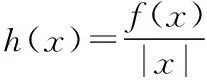
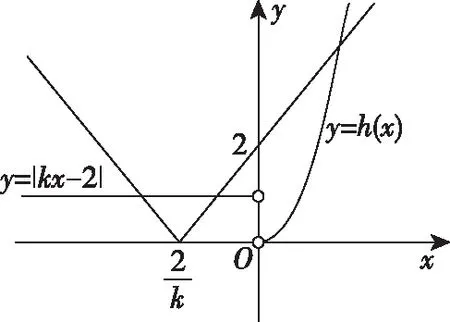
圖6

③當k>0時，

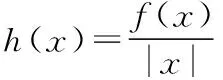
當x>0時，如圖7，當y=kx-2與y=x2相切時，聯立方程得x2-kx+2=0，

圖7

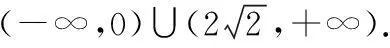
評析:本題考查函數與方程的應用，考查數形結合思想、化歸與轉化思想，由方法一得出g(x)的解析式，分類討論，由滿足g(x)有四個零點，求出相應參數的取值范圍，解題過程中用到零點存在性定理；方法二、三將零點問題轉化為兩個函數圖象交點個數問題，入手較易，但第三種方法等式兩邊同時除以|x|很巧妙，需要有很高的數學素養，后兩種方法利用數形結合的思想方法，使得分類更加直觀.

例3:(2020·新高考Ⅰ卷(供山東省使用)·21)已知函數f(x)=aex-1-lnx+lna.

(Ⅰ)當a=e時，求曲線y=f(x)在點(1，f(1))處的切線與兩坐標軸圍成的三角形的面積；

(Ⅱ)若f(x)≥1，求a的取值范圍.

解法一:分類討論，尋求零點

教師:第一問我們不再研究，重點看第二問，如何用分類整合的思想去解決此題，應如何思考？

學生6:利用導數研究，若f(x)≥1，只須f(x)min≥1.

教師:如何去求f(x)min？

學生6:對函數f(x)進行求導，得出f′(x)并判斷其單調性.

教師:因為f(x)=aex-1-lnx+lna,

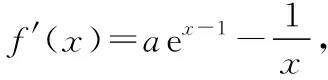
即f′(x)在(0,+∞)上單調遞增.

教師:至此我們得出了f′(x)在(0,+∞)上單調遞增，但是怎樣的趨勢看不出來，下面需要對a再進行分析.

學生7:我發現f′(1)=a-1，故當a=1時，f′(1)=0,

從而當x∈(0,1)時，f′(x)<0；當x∈(1，+∞)時，f′(x)>0，

即f(x)在(0,1)上為減函數，在(1，+∞)上為增函數，

f(x)min=f(1)=1,所以f(x)≥1成立.

教師:很好，有了a=1的情況，我們就有了分類標準.

學生8:當a>1時，當x→0時，f′(x)→-∞;當x→+∞時，f′(x)→+∞，根據零點存在性定理，?x0>0，使得f′(x0)=0.

教師:利用極限的思想為我們提供了解題的思路，但不嚴密，我們能否找到兩個值m,n，使得f′(m)f′(n)<0呢？

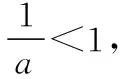
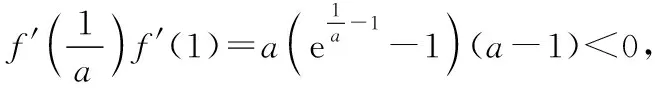
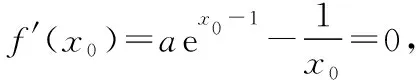
教師:很好，到此我們找到一個零點x0，滿足f′(x)=0，

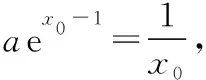
因此f(x)min=f(x0)

=aex0-1-lnx0+lna

=2lna+1>1，

f(x)>1,所以f(x)≥1恒成立.

教師:當0

學生10:當0

所以f(1)<1,f(x)≥1不是恒成立.

教師:很好，綜上所述，實數a的取值范圍是[1,+∞).

教師:在a>1時，我們通過零點存在性定理，得出f(x)在(0,+∞)存在最小值f(x)min=f(x0)，我們現在繼續觀察題目中的f(x)=aex-1-lnx+lna，通過放縮法，你能得出什么樣的結論.

學生11:因為a>1,f(x)=aex-1-lnx+lna中含a的項，可以進行放縮，得出f(x)=aex-1-lnx+lna>ex-1-lnx，然后再借助兩個重要不等式進一步放縮，ex-1≥x-1+1=x,lnx≤x-1.

教師:好，下面按此思路，同學們完成解答過程，可以看出ex≥x+1及其變形在處理導數問題時的重要性.

解法二:放縮變形，分類討論

當0

所以f′(x)在(0,+∞)上單調遞增.又因為f′(1)=0，所以當x∈(0,1)時，f′(x)<0；當x∈(1,+∞)時，f′(x)>0，所以f(x)min=f(1)=1,f(x)≥1成立.

當a>1時，易證ex≥x+1，從而可以得出ex-1≥x,lnx≤x-1，所以f(x)=aex-1-lnx+lna>ex-1-lnx≥[(x-1)+1]+(-x+1)=1.

綜上所述，實數a的取值范圍是[1,+∞).

評析:函數導數問題中的不等式恒成立問題一直是教學的重點，因為其中既含有參數又含有變量，能很好地考查學生分析問題、解決問題的能力.教學過程中要讓學生展示其思維過程，讓學生獲得學習的成就感，在最近發展區域內，讓學生通過深入思考，總結出解決導數問題分類討論的方法，通過分類與整合提升學生對問題的認知，提升其核心素養.