2020年北京卷解析幾何試題高等幾何背景探究

北京 蘇漢杰

2020年是北京新高考文理合卷的第一年，從整套試卷的試題結構和靈活性來看，與往年相比有一些創新，但是北京卷的整體命題思路沒有改變，一些優秀的方面得到了很好的傳承.比如第20題解析幾何，既有高等幾何的背景，又重點考查了先猜后證、化歸與轉化的數學思想和用坐標方法解決幾何問題的基本解題思路，是一道非常好的題目.下面筆者對這道題目進行探究.

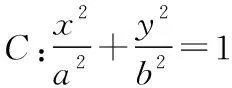
(Ⅰ)求橢圓C的方程；

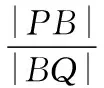
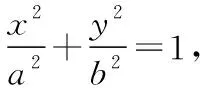
第(Ⅱ)問中，變化量是過點B(-4，0)的直線l的斜率，其他的量都可以由其導出，所以運算的思路非常清晰.我們不妨設直線l的方程為x=ny-4，M(x1，y1)，N(x2，y2)是橢圓C與直線l的兩個交點，直線MA，NA以及點P，Q都可以用點M和點N的坐標來表示，并最終在運算過程中替換為n的表達式，達到化簡求值的目的.

詳解：(Ⅰ)把A(-2，-1)代入橢圓方程，

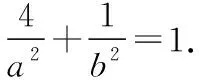
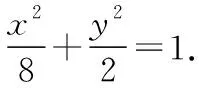
(Ⅱ)當直線l的斜率為0時，即直線l：y=0，

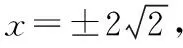
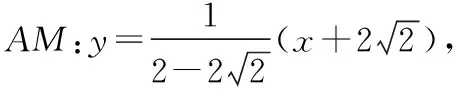
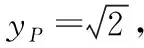
當直線l的斜率不為0時，設其方程為x=ny-4，M(x1,y1),N(x2,y2)，

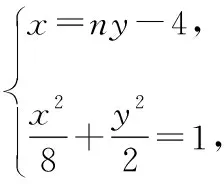
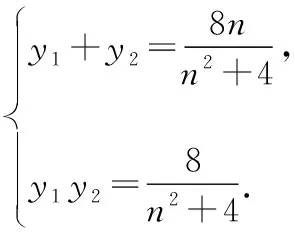
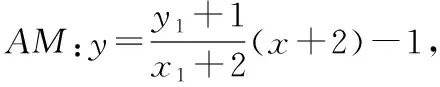
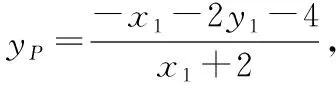
又x1=ny1-4，x2=ny2-4，

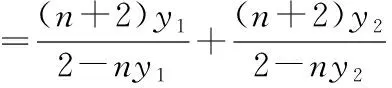
將①式代入，得yP+yQ=0，

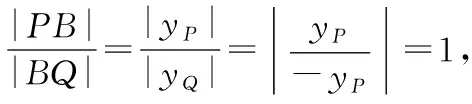
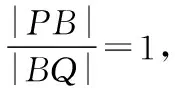
第(Ⅱ)問這種變化中的不變性是射影幾何的基本性質，是北京卷和其他高考試卷解析幾何試題的重要背景.這些知識是高等幾何的知識，考生在高中階段是不要求掌握的.但是作為教師，如果能夠掌握相關的知識，就能夠做到不但知其然，還知其所以然，能夠站得更高，看得更遠.下面筆者來給出相關的定義、定理和有關推論：

1.交比

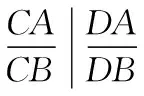
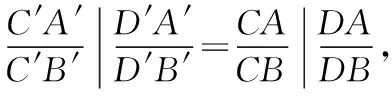
2.調和共軛

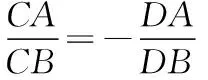
給定二次曲線C與點P，Q，如果P，Q兩點的連線與二次曲線C交于兩點M，N，且(PQMN)=-1，則稱P，Q關于二次曲線C調和共軛；

(2)性質：不在二次曲線上的一個定點P關于一條二次曲線的調和共軛點的軌跡是一條直線.

3.極點、極線

(1)定義：不在二次曲線上的定點P關于該二次曲線的調和共軛點的這條直線，叫做點P關于此二次曲線的極線，P為這條直線關于此二次曲線的極點.

如圖，P是不在圓錐曲線上的點，過P點引兩條割線依次交圓錐曲線于E，F，G，H，連接EH，FG交于N，連接EG，FH交于M，則直線MN為點P對應的極線.同理PM為點N對應的極線，PN為點M對應的極線.△MNP稱為自極三角形.

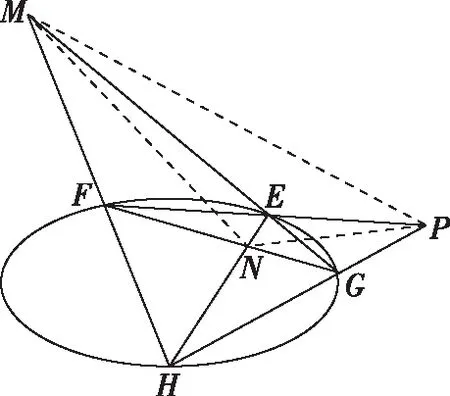
(2)性質

①如圖，設點P關于有心圓錐曲線C(設其中心為O)的調和共軛點為點Q，直線PQ經過圓錐曲線的中心，則有OR2=OP·OQ；反之，若有OR2=OP·OQ成立，則點P與Q關于圓錐曲線C調和共軛.

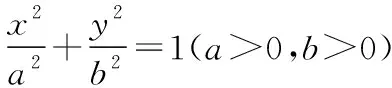
(以上一些定義、定理和性質的證明過程略，感興趣的老師可以查閱相關資料了解詳細證明過程.)

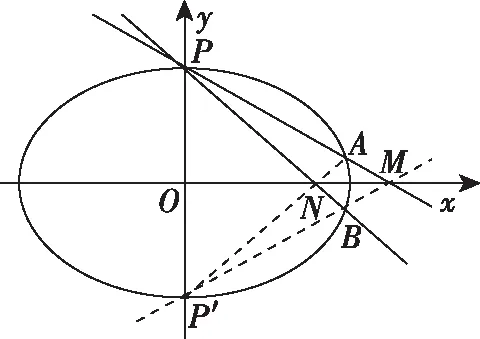
在此基礎上，我們從極點、極線理論的角度來看看2020年北京高考解析幾何題的高等幾何背景，如圖所示.

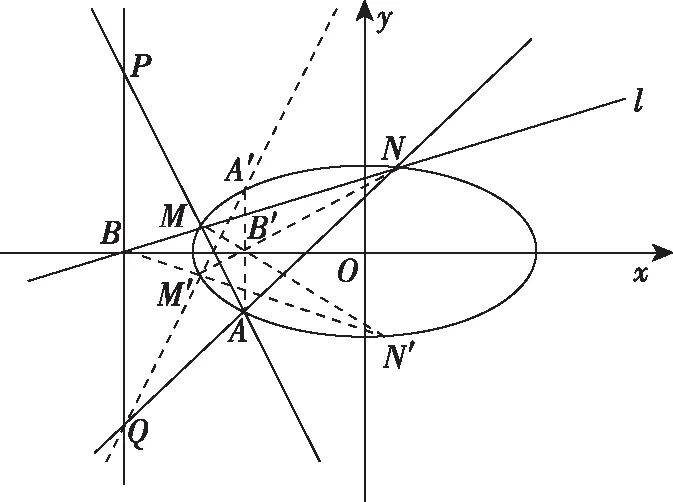
設點A，M，N關于x軸的對稱點分別是A′，M′，N′，AA′與x軸的交點是B′，因為a2=8，B(-4，0)，B′(-2，0)，所以由性質①可知，點B與點B′關于曲線C調和共軛，由極點、極線的定義可知，B′是MN′與M′N的交點，B是MN與M′N′的交點，由性質②可知，直線x=-4是點B′關于曲線C的極線.下面我們需要說明直線A′M′與直線NA的交點與點Q重合，因為直線AA′與直線M′N的交點是B′，所以A′M′與NA的交點與點B′關于曲線C調和共軛，所以交點在直線x=-4上，也就是點Q.因此，由直線AM與直線A′M′的對稱性可知，|PB|=|BQ|.

了解了這道題的高等幾何背景到底有什么幫助呢？可以把這個結論進行遷移和一般化，這是解析幾何命題經常用的方法.以下面幾道北京卷解析幾何試題為例來探析這幾個不同題目的相同幾何背景.

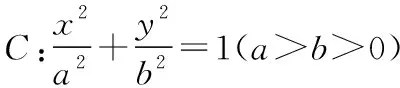
(Ⅰ)求橢圓C的方程，并求點M的坐標(用m，n表示)；

(Ⅱ)設O為原點，點B與點A關于x軸對稱，直線PB交x軸于點N.問：y軸上是否存在點Q，使得∠OQM=∠ONQ？若存在，求點Q的坐標；若不存在，說明理由.

分析：此題大家非常熟悉，就不再贅述其詳細分析和解答過程，下面來看看它的幾何背景，如圖所示.

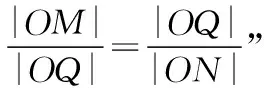
由極點、極線定義及性質①可知，M，N是一對位于橢圓的對稱軸上的共軛點，|OM||ON|=a2=2，所以“存在點Q，使得∠OQM=∠ONQ”.

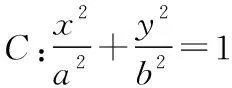
(Ⅰ)求橢圓C的方程；

(Ⅱ)設O為原點，直線l:y=kx+t(t≠±1)與橢圓C交于兩個不同點P，Q，直線AP與x軸交于點M，直線AQ與x軸交于點N.若|OM|·|ON|=2，求證：直線l經過定點.

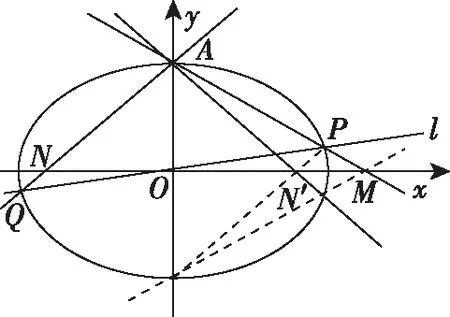
分析：此題可以說與上一題的背景完全相同，橢圓的方程也完全一樣，只是把2015年試題中的所求|OM|·|ON|=2改成了已知.所以只有當直線l經過的定點為原點時，直線AN才能對稱到AN′，此時M，N′是一對位于橢圓對稱軸上的共軛點，能滿足|OM||ON|=a2=2.

3.(2019·北京卷理·18)已知拋物線C：x2=-2py經過點(2，-1).

(Ⅰ)求拋物線C的方程及其準線方程；

(Ⅱ)設O為原點，過拋物線C的焦點作斜率不為0的直線l交拋物線C于兩點M，N，直線y=-1分別交直線OM，ON于點A和點B.求證：以AB為直徑的圓經過y軸上的兩個定點.

分析：理科的這道題是把圓錐曲線由橢圓換成了拋物線，求證“以AB為直徑的圓經過y軸上的兩個定點”即證“在y軸上存在點P，使得|FP|2=|FB||FA|”當然，在計算的過程中，我們也可以轉化成斜率來表示這個關系.其幾何背景是|FB′||FA|=|FR|2=4，如圖，B′是點B關于y軸的對稱點，R是直線y=-1與拋物線的一個交點.

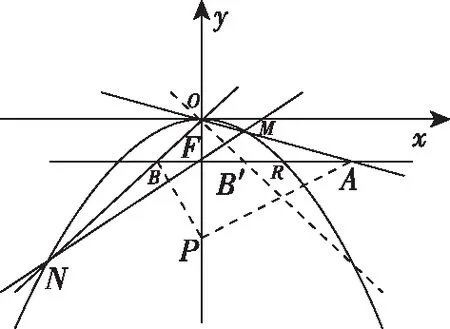
這三道題其實是一個幾何背景，把二次曲線由橢圓換成拋物線來考(其實也可以換成雙曲線)，或者對條件和結論進行變換再考，是在一個背景下考查用解析幾何的方法證明同一個幾何性質.由于高中階段沒有學習過高等幾何的相關知識，所以對于考生來說，沒有雷同之嫌，都是新的題目，這些題目都考查了解析幾何中探索實踐、先猜后證和化歸與轉化的基本思想方法.

經過這樣一番對比研究以后，對2020年北京卷解析幾何試題有沒有什么新的想法呢？可以繼續探究下去，看看還能得出哪些結論和性質，能夠變換出哪些不同的題目.

變式探究：

(2)把橢圓的方程換為雙曲線或者拋物線的方程，結論仍然成立；

(3)更一般的結論：在求方程時用了點A的坐標，其實在第二問時完全可以不用橢圓上的點A，而使用橢圓外的點，只要點A在點B對應的極線上，結論也是完全可以成立的.這一步的引申與前兩個相比不是那么顯而易見.

如圖，AM與橢圓的另一個交點為E，AN與橢圓的另一個交點為F，MF與EN的交點為R，則R與A調和共軛，又因為點B對應的極線是過點A與x軸垂直的直線，所以△ABP是自極三角形，所以點B，E，F三點共線.

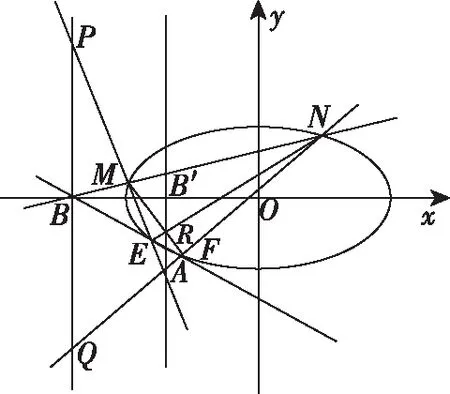
如圖，點E關于x軸的對稱點為E′，點F關于x軸的對稱點為F′，點B與點B′調和共軛，所以E′，B′，F三點共線.

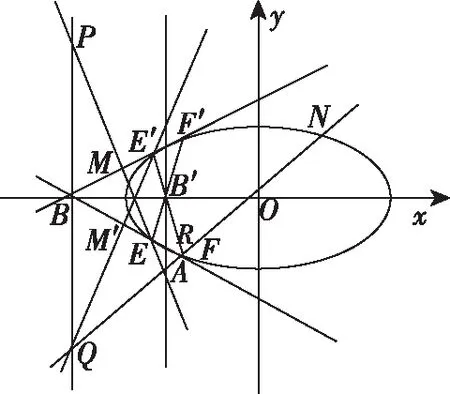
如圖，易知M′，B′，N三點共線，因為E′F與M′N交于點B′，所以E′M′與NF的交點在點B的準線上，也就是點Q.因此，此命題成立.

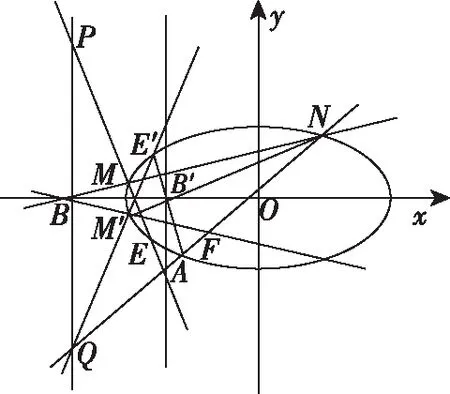
(4)由上面的結論，如果把|PB|=|BQ|當成已知，就可以求證點A在一條定直線上，這又是另外一個題目了.