多點激勵簡支梁橋車橋耦合振動響應

韓智強， 李路遙， 周勇軍， 李華騰， 劉世忠， 晉民杰

(1.太原科技大學交通與物流學院，太原 030024； 2.長安大學公路大型結構安全教育部工程研究中心， 西安 710064)

隨著國民經(jīng)濟飛速發(fā)展，交通狀況日趨復雜，車輛與橋梁相互影響較為突出[1]。古典車橋耦合振動分析通常將車輛簡化為集中力、簡諧力或質量塊等，橋梁被簡化為有限梁單元進行求解。針對車橋耦合方法的求解，中外學者提出勻速移動常力、勻速移動簡諧力、勻速滾動質量、勻速彈簧-質量等相關計算模型，使得車橋耦合仿真計算成為可能。隨著計算機技術快速發(fā)展，實現(xiàn)車橋耦合精細化分析成為可能。李江龍等[2]基于車輛動力響應功率譜密度，采用自編軟件，對橋梁安全性進行評價分析；Shen等[3]基于模型縮聚理論，采用模態(tài)分析和車橋耦合瞬態(tài)分析，實現(xiàn)多自由度車橋耦合仿真分析；肖乾等[4]分析胎壓變化對車橋系統(tǒng)的振動影響，得出胎壓變化對系統(tǒng)橫向動力響應和走行滑移量有一定影響。趙越等[5]基于等參映射及改進折半法建立車橋耦合分析系統(tǒng)，建立多種精細化車輛模型，并通過全過程迭代法求解車橋耦合系統(tǒng)，其收斂速度較快；許漢錚等[6]采用17自由度三軸空間車型，分析橫豎向車橋耦合曲線橋的動力響應，結果表明:曲線橋梁前兩階以豎向振動為主，且橫豎向車橋耦合在曲線橋梁動力分析中較為重要；在多車車橋耦合方面，相關學者也開展了相關研究；王娟等[7]采用多個集中彈簧-阻尼-質量系統(tǒng)作用于簡支梁橋時，隨著各個敏感參數(shù)變化，橋梁動態(tài)響應變化；經(jīng)薇等[8]建立多車激勵簡支梁橋車橋耦合分析模型，采用頻域和時域進行數(shù)值分析，并根據(jù)邊界條件驗證了方法的正確性。

上述研究成果主要集中于單車車輛分析或者多車等效集中彈簧-阻尼-質量系統(tǒng)，分析橋梁振動特性，對橋梁沖擊系數(shù)的研究相對較少。因此，基于車輛動力學的相關原理，理論推導多車車輛動力學方程，采用模態(tài)綜合法建立多車車橋耦合分析系統(tǒng)，并與相關文獻算例結果進行對比分析，驗證方法的正確性，并考慮在一定車輛間距和數(shù)量下橋梁的動力響應變化，計算其沖擊系數(shù)，并與多國規(guī)范值[9]進行比較，相關研究成果可為公路橋梁多車車橋耦合分析和沖擊系數(shù)的計算提供指導。

1 基于模態(tài)綜合法的多車車橋耦合分析系統(tǒng)

1.1 基本假定

(1)車輛在橋面行駛的過程中車輪時刻緊貼與橋面不發(fā)生分離。

(2)忽略橋梁橫截面的變形。

(3)橋梁采用瑞雷阻尼，即橋梁阻尼矩陣與質量矩陣和剛度矩陣呈線性相關[10]。

1.2 車輛動力學方程的建立

以多輛兩軸車為對象，根據(jù)車輛的動力特性，將其簡化為4自由度的平面車型，包括車體的沉浮和點頭，前后車輪浮沉。兩軸車簡化模型如圖1所示，圖1中：miv和Jiv為第i輛車車體質量和點頭轉動慣量；mix1和mix2為第i輛車前后懸架和輪對質量之和；cis1、cis2和kis1、kis2為第i輛車前后懸架彈簧阻尼系數(shù)和剛度系數(shù)；cit1、cit2和kit1、kit2為第i輛車前后車輪的阻尼系數(shù)和剛度系數(shù)；ziv和θiv代表第i輛車車體浮沉位移和點頭角位移；yd和wj分別代表車輪位移和車輪與橋面接觸點處的橋面豎向位移。

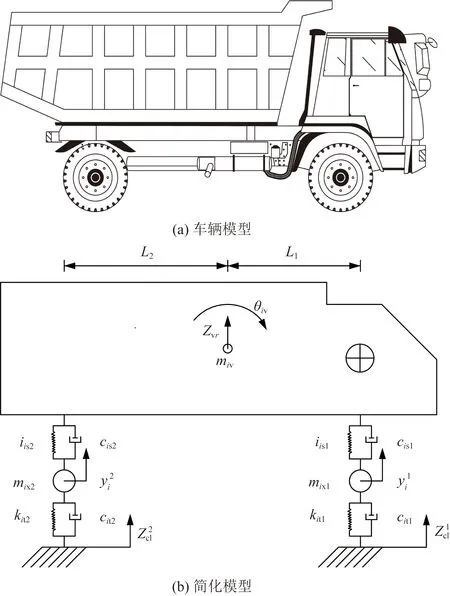
L1和L2為兩軸車輛前后懸架至車輛形心間縱向距離，m; Zvr為車體豎向位移，mm; yi1為第i輛前懸架豎向位移，mm; yi2為第i輛后懸架豎向位移，mm;ZCl1為第i輛前輪對豎向位移，mm; ZCl2為第i輛后輪對豎向位

根據(jù)D’Alembert原理建立多車動力學運動方程[11]，如式(1)所示:

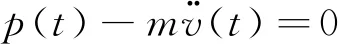
(1)

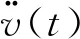
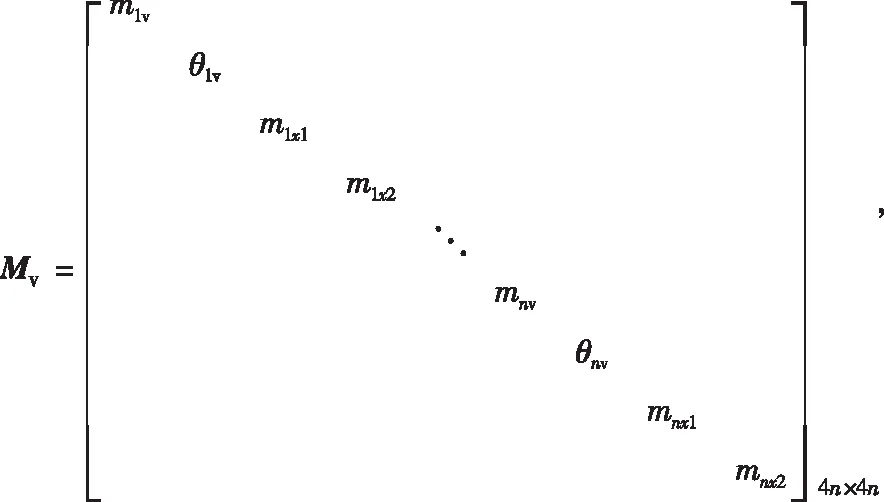
分別對車體、懸架和輪對的4自由度進行受力分析，根據(jù)公式(1)建立n輛車車體動力平衡方程，整理成矩陣形式，如式(2)所示：

(2)

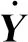
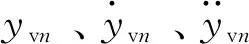
1.3 橋梁動力方程的建立

通過有限元軟件建立橋梁仿真模型，通過模態(tài)分析獲取橋梁的固有角頻率ωj和振型向量Φ，采用振型疊加法構造橋梁模態(tài)方程，并將結構物理坐標轉換為模態(tài)坐標，如式(3)[12]所示：

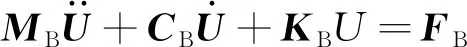
(3)

式(3)中：MB=ΦTMΦ為橋梁結構正則化模態(tài)質量矩陣；其中M為橋梁結構質量矩陣；CB=ΦTCΦ為橋梁結構正則化模態(tài)阻尼矩陣，其中C為橋梁結構阻尼矩陣；KB=ΦTKΦ為橋梁結構正則化模態(tài)剛度矩陣；FB=ΦTF為橋梁結構模態(tài)力向量，其中F為車輛作用橋梁的荷載向量：

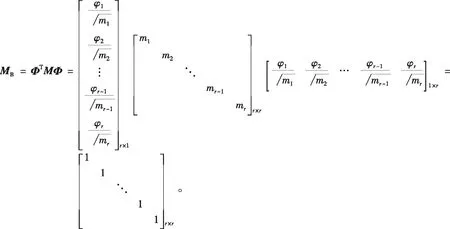
同理可得出CB和KB矩陣：

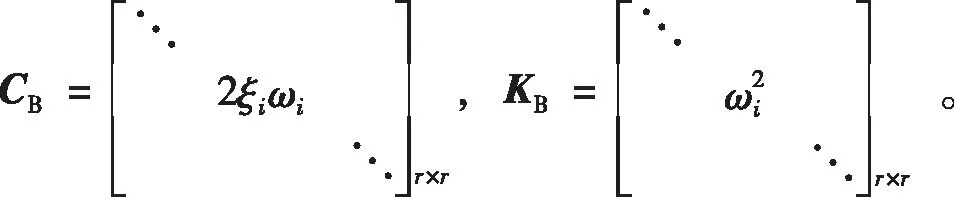
式中：ωi為橋梁第i階自振圓頻率；ξi為橋梁第i階頻率對應的阻尼比。

1.4 車橋耦合相互作用分析

如圖2所示，假設車輛在橋面行駛過程中車輪時刻緊貼與橋面不發(fā)生分離，那么j點處車輪下緣的豎向位移為ydj。

圖2 輪-橋接觸點位移協(xié)調關系

ydj=wj+rj

(4)

式(4)中:rj為橋面不平整度,mm; 其他類同。

車輪下緣的豎向速度為

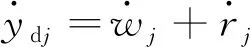
(5)

因此，車輪彈簧的壓縮量和黏滯阻尼器的相對速度為

Δyj=yj-ydj=yj-(wj+rj)

(6)

(7)

式中:yj為車輪的浮沉位移,mm。

在求解j點處車橋系統(tǒng)的位移后，可推導車輛與橋梁在j點處的相互作用力fvbj，如式(8)所示。

(8)

(9)

式中:ktj為車輪的剛度系數(shù)；ctj為車輪的阻尼系數(shù)；v為車輛行車速度。

將式(1)～式(9)進行整理，得出多車激勵車橋耦合系統(tǒng)振動方程[13]為

(10)

式(10)中：MB為橋梁質量矩陣；CB為橋梁阻尼矩陣；CvB為橋車阻尼耦合矩陣；KB為橋梁剛度矩陣；KvB為橋車剛度耦合矩陣；FB為橋梁所受外力矩陣。

2 沖擊系數(shù)計算方法

車輛荷載通過橋梁時，由于激振力作用橋梁產(chǎn)生的動力響應，形成沖擊效應[9]，為簡化計算，采用沖擊系數(shù)進行分析，沖擊系數(shù)計算示意圖如圖3所示，計算公式如式(11)所示:

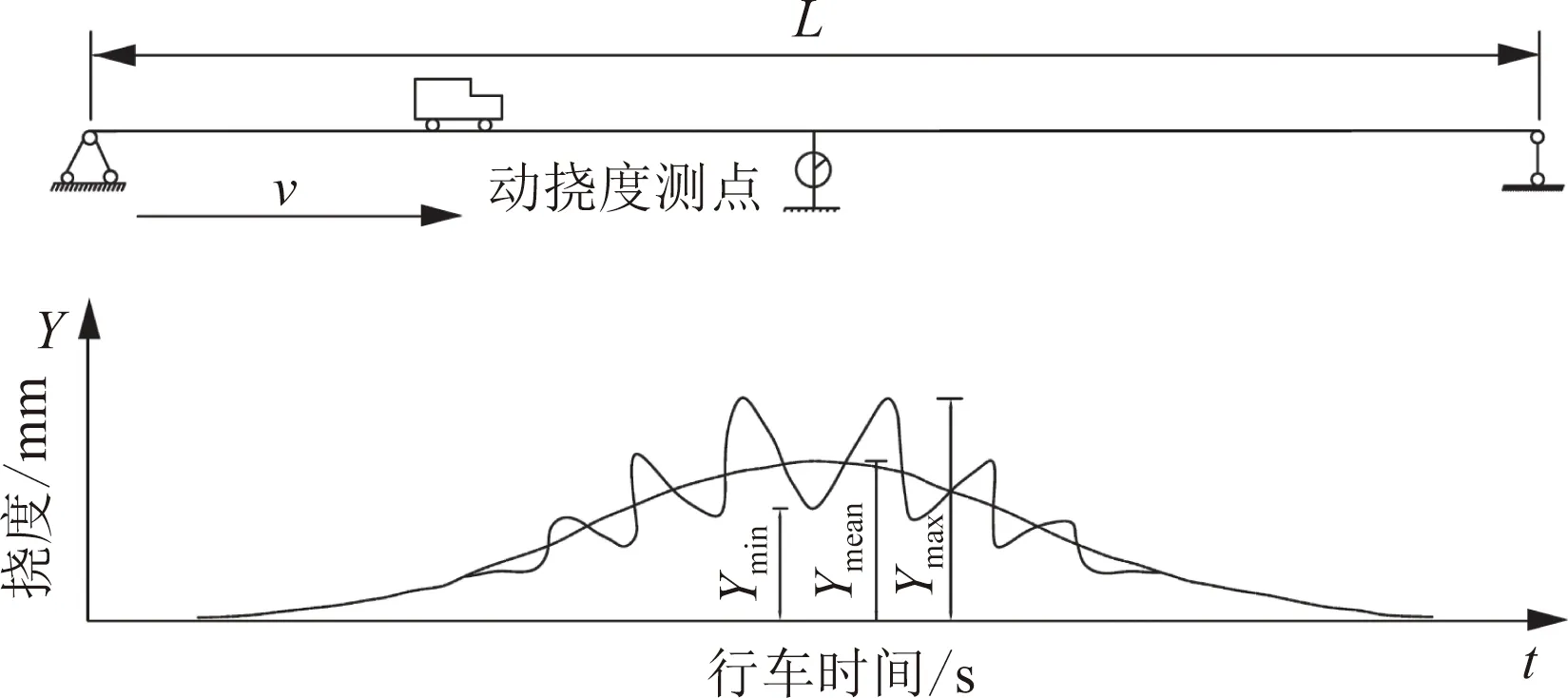
圖3 車輛激勵下橋梁跨中截面沖擊系數(shù)計算示意圖

μ=1-Ydmax/Yjmax

(11)

式(11)中:Ydmax為車輛過橋時，橋梁跨中截面動撓度的最大值；Yjmax為橋梁跨中截面的靜撓度最大值。

2.2 各國沖擊系數(shù)計算方法

(1)美國橋梁設計規(guī)范(AASHTO LRFD—2018)。橋面接縫-所有極限狀態(tài):μ=0.75；所有構件疲勞鍛煉破壞：μ=0.15；其他狀態(tài):μ=0.33。

(2)加拿大橋梁設計規(guī)范 (DHBDC2006)。規(guī)范中沖擊系數(shù)與汽車的輪軸數(shù)有關:當車輛軸數(shù)為1時，μ=0.4；當車輛軸數(shù)為2時，μ=0.3；當車輛軸數(shù)大于等于3時，μ=0.25。

(3)英國橋梁設計規(guī)范(BSI2006)中規(guī)定不同交通荷載沖擊系數(shù)取值0.25。

(4)德國(DIN1072)規(guī)定。

μ=0.4-0.008L

(12)

式(12)中:L為橋梁跨徑,m。

(5)中國公路橋涵通用規(guī)范[9](JTG D60—2015)。沖擊系數(shù)與結構基頻f的函數(shù)表達式為

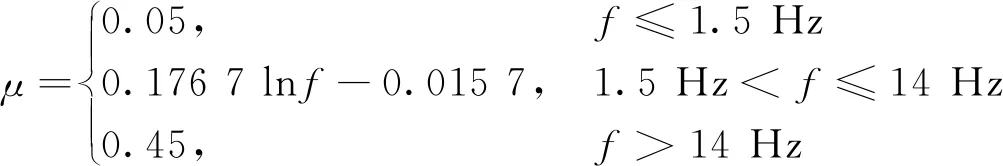
(13)

式(13)中:f為橋梁結構的基頻,Hz。

3 仿真驗證

為驗證本文方法的正確性，通過自編程序對參考文獻[14]算例進行計算分析，相關參數(shù)如表1、表2所示，計算結果如圖4～圖6所示，由于篇幅有限，僅列舉部分對比數(shù)據(jù)、對比結果。

表1 車輛技術參數(shù)

表2 橋梁技術參數(shù)

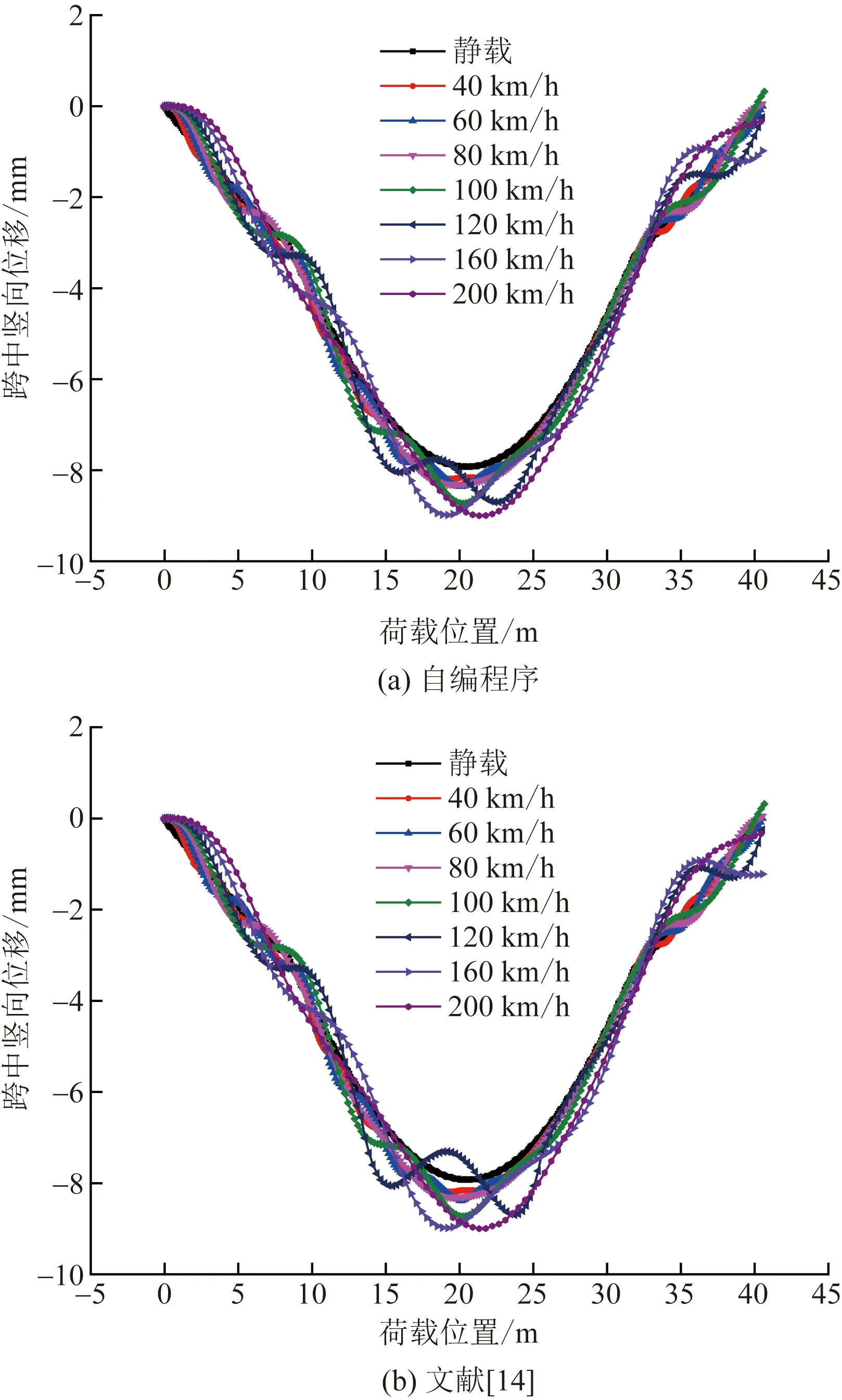
圖4 32 m簡支梁不同速度荷載作用下跨中位移時程曲線

如圖4～圖6所示，各個截面在不同車速下位移響應結果與文獻[14]的計算結果較為接近，其曲線走勢也較為吻合，不同行車速度下自編程序計算結果與文獻[14]結果的相對誤差均小于6%，驗證了方法的正確性和適用性。

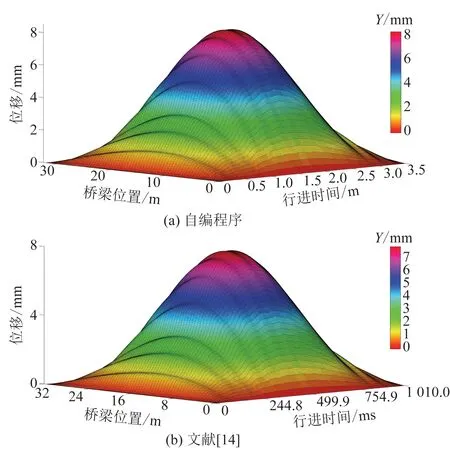
圖5 速度v=40 km/h 的位移響應

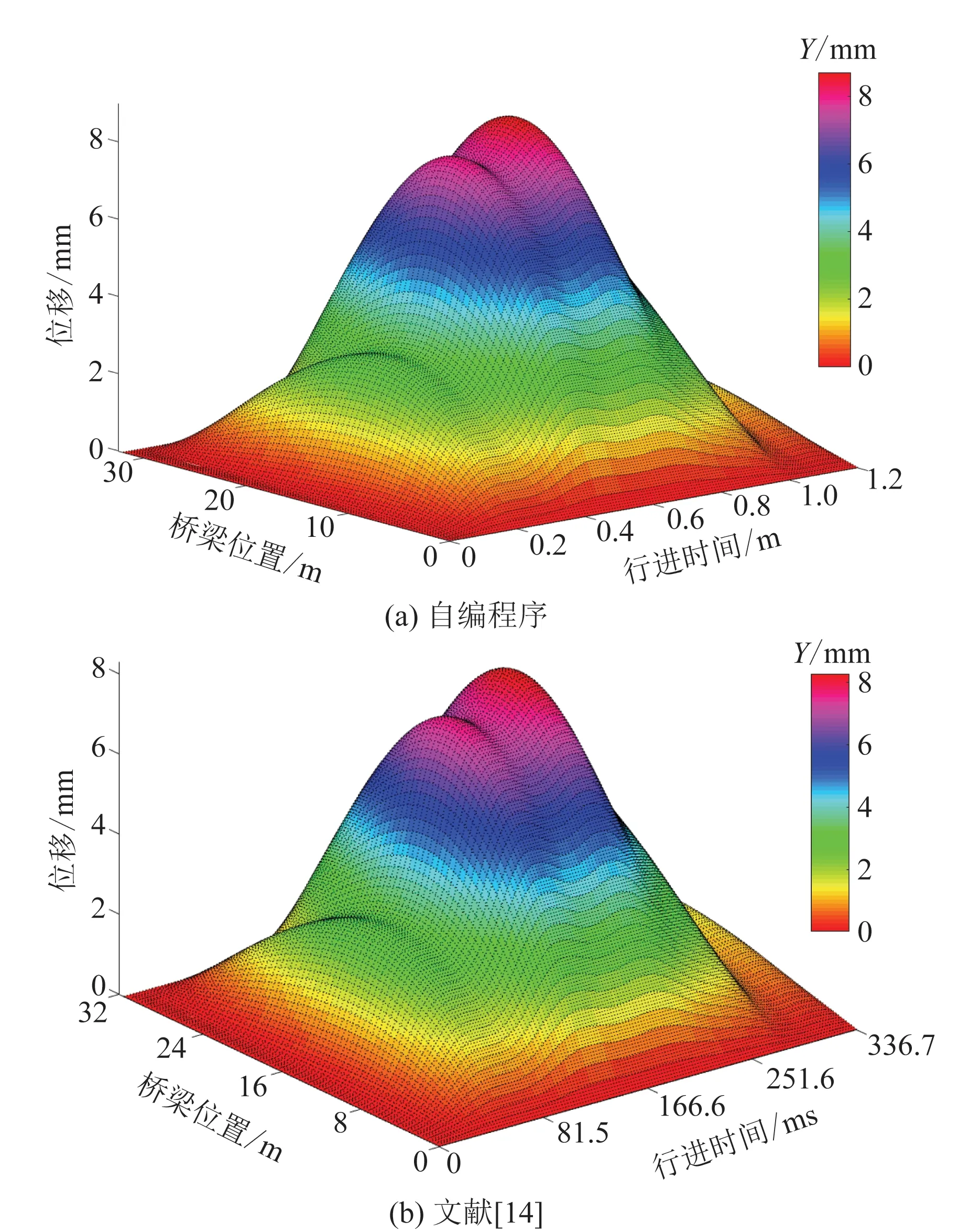
圖6 速度v=120 km/h 的位移響應

4 多車車橋耦合振動研究

單輛激勵通過橋梁時，結構動力響應能夠一定程度上反映橋梁振動規(guī)律，但與實際情況有較大不同，為考慮縱向多車激勵，車輛以車隊形式通過橋梁時，其車橋相互作用更為真實，因此，開展多車車橋耦合振動分析及沖擊系數(shù)研究有一定現(xiàn)實意義。

在多車車橋耦合分析時，車輛間距的不同，橋梁振動響應也不盡相同。為了充分了解不同間距對橋梁動力響應，定義車輛間距比p，如圖7和式(14)所示。

圖7 縱向多車激勵車橋耦合分析示意圖

(14)

式(14)中:p為車輛間距比；li為相鄰兩車車輛間距,m；L為橋梁跨徑,m。

4.1 不同車輛間距比下橋梁位移響應分析

為得到不同車輛間距比下橋梁的結構響應，對兩輛車行駛通過簡支梁進行仿真分析，其中橋面不平整度采用B級，通過自編程序建立了不同車輛間距比模型，并進行車橋耦合仿真計算，如表3和圖8、圖9所示。

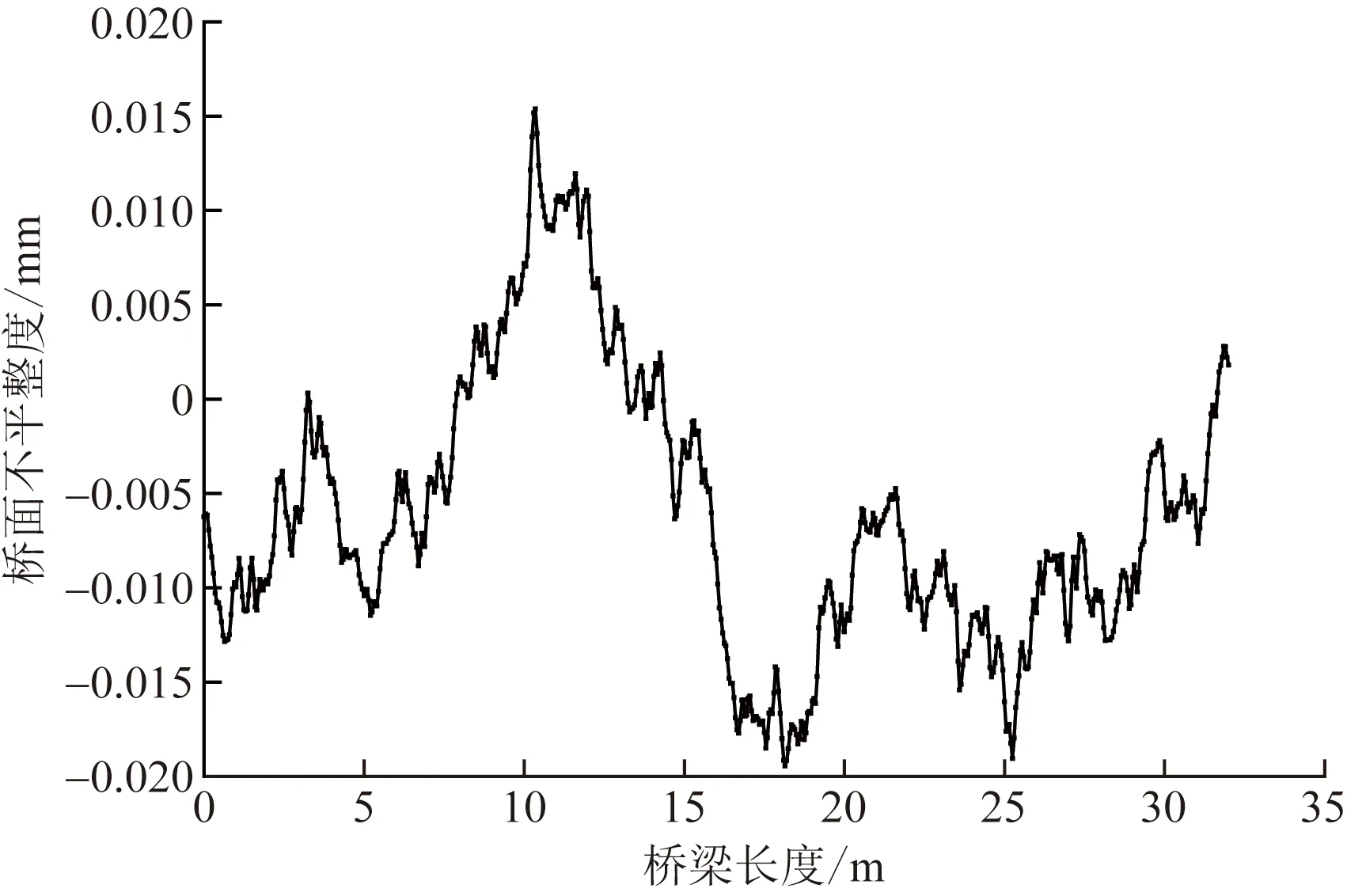
圖8 B級橋面不平整度

表3 不同車輛間距比

從圖9可知，當兩輛車輛以不同車輛間距比在橋上行駛，從上橋到下橋，橋梁跨中位移也不盡相同。隨著車輛間距比p減小，橋梁跨中最大豎向位移呈增加趨勢，當p=1/8和p=1/4時最大豎向位移明顯增加，當p=1時，最大豎向位移接近單車時的橋梁位移響應。

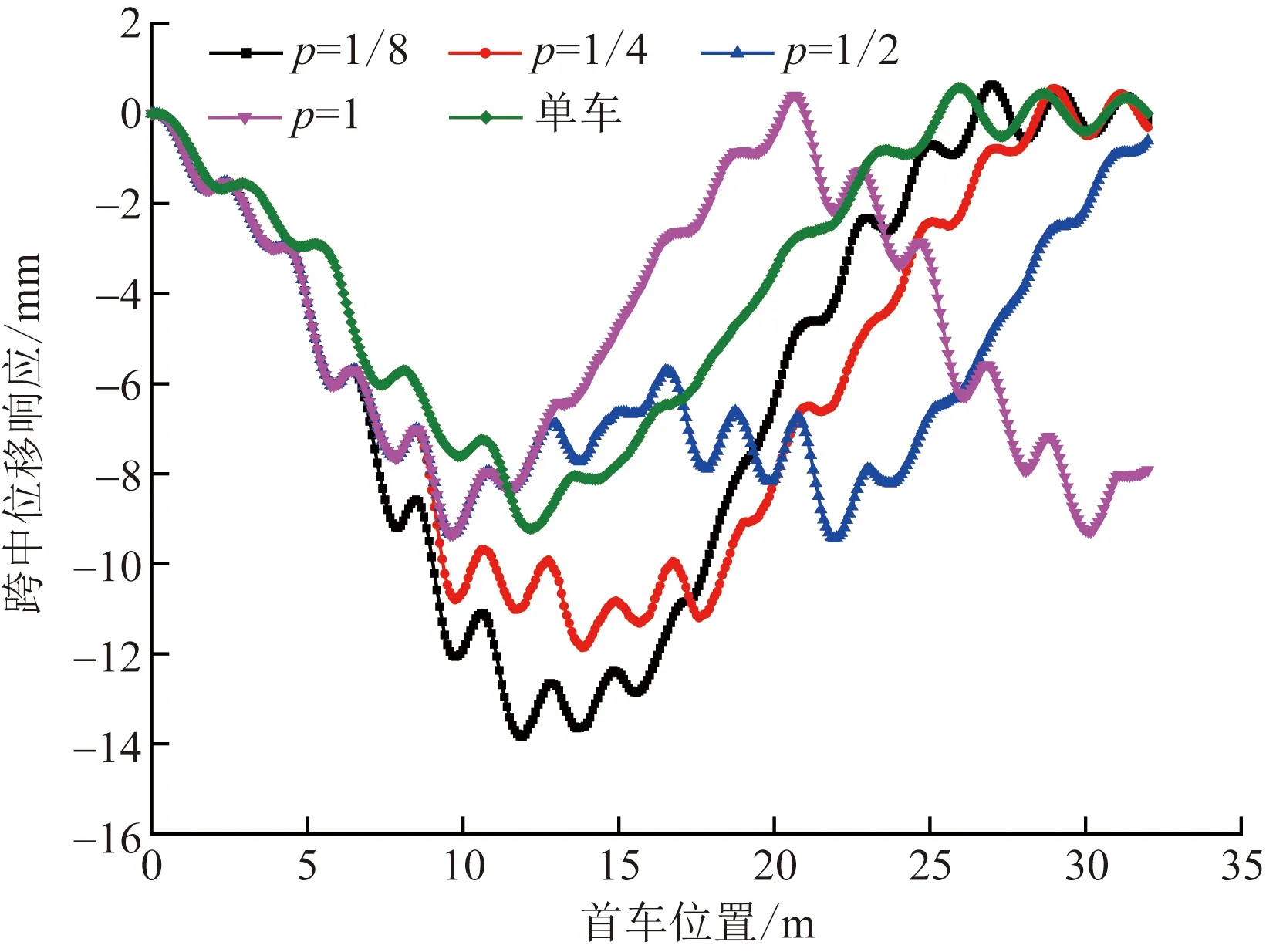
圖9 不同車輛間距比橋梁跨中位移響應

4.2 不同車輛數(shù)量橋梁位移響應分析

因此，本文分析不同車輛在不同車輛間距下，通過簡支梁橋時橋梁位移響應情況[15]。通過選用2～6輛車作為研究對象，結合單車通過橋梁時車速對橋梁振動響應的影響，選用60 km/h作為車輛行駛速度，分析不同工況下的橋梁振動響應，如圖10所示。

根據(jù)圖10可知，橋梁跨中最大豎向位移隨車輛數(shù)增加而逐步增大，但車隊中車輛數(shù)超過一定車輛時，橋梁跨中最大豎向位移不再增加，如當p=1/4時，車輛達到4輛車后，跨中位移達到極值，為13.51 mm， 為單車過橋時的1.4倍，兩車過橋1.3倍，超過4輛車時，橋梁跨中最大豎向位移極值點不在增大。究其原因:隨著車輛增加，橋梁的振動響應相互疊加，豎向位移逐漸增大；但當車輛數(shù)達到極值點后，由于車輛下橋時，橋梁阻尼系統(tǒng)對結構能量的耗散，與新駛入車輛對橋梁振動相互疊加，達到動態(tài)平衡，從而引起跨中豎向位移不在增大。

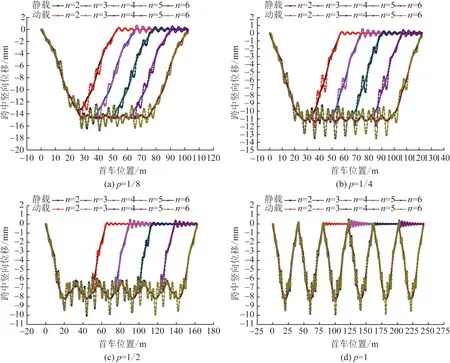
圖10 不同數(shù)量車輛下橋梁跨中豎向位移時程曲線

4.3 多車車橋耦合沖擊系數(shù)研究

通過對第4.2節(jié)相關數(shù)據(jù)進行整理，采用式(11)計算跨中截面位移沖擊系數(shù)，并與不同國家規(guī)范沖擊系數(shù)的規(guī)定值進行對比分析，如表4、表5所示。

由表4、表5可知:不同間距和車輛作用下，沖擊系數(shù)計算值介于0.10～0.23；并與不同國家規(guī)范值進行比較，得到在車輛較多時，德國規(guī)范和中國規(guī)范的沖擊系數(shù)小于仿真結果的最大值，其他國家的規(guī)范值大于規(guī)范計算值，表明:這兩國規(guī)范在多車激勵車橋耦合分析時，不太安全，建議在后續(xù)分析中，應考慮多車激勵的影響。

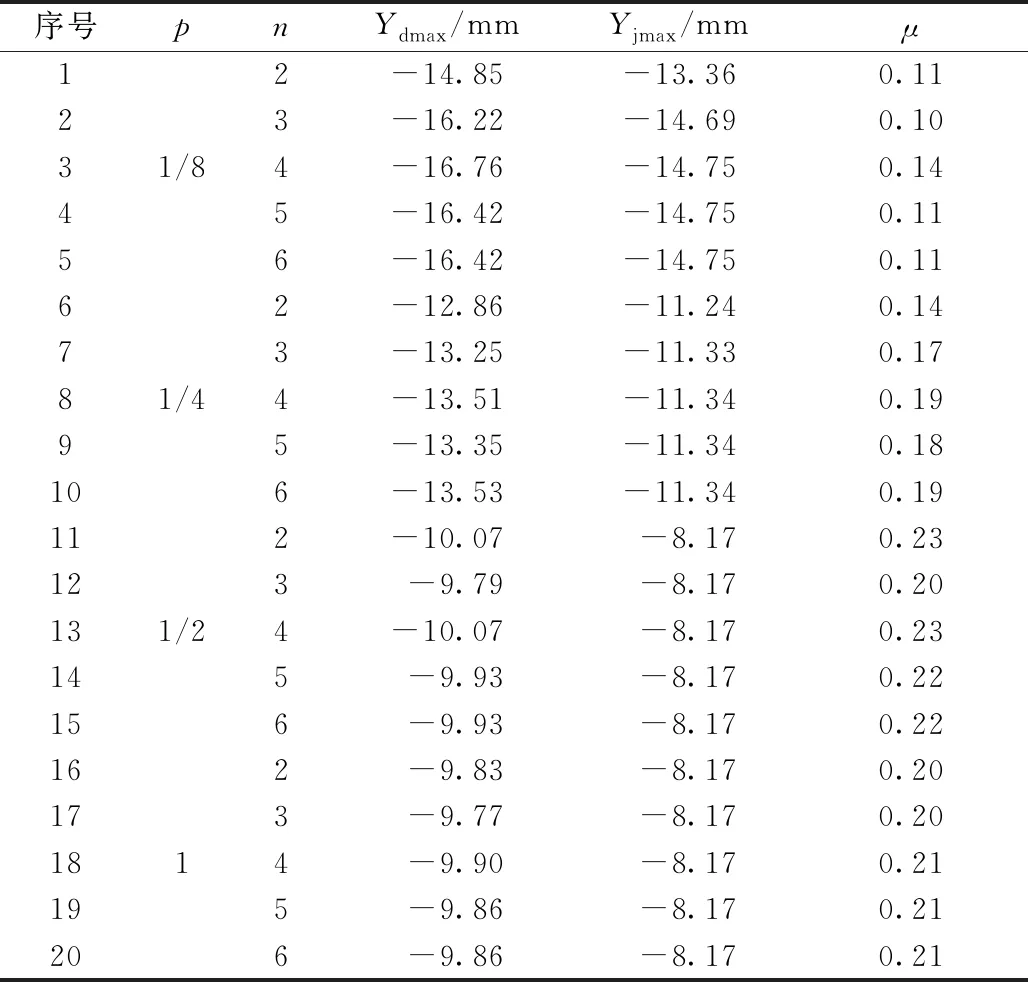
表4 不同工況下跨中截面豎向位移沖擊計算值

表5 不同國家沖擊系數(shù)規(guī)范值

5 結論

(1)采用模態(tài)綜合法建立多車的車橋耦合分析模型，通過與相關文獻算例進行對比分析，結果表明:跨中位移響應計算結果相對誤差均在6%以內(nèi)，驗證了方法的正確性和適用性。

(2)分析了車輛不同間距下，橋梁跨中截面豎向位移的時程曲線，即當車輛間距比減小時，最大豎向位移明顯增加，當p接近1時，最大豎向位移接近單車時的位移響應。

(3)分析了在給定車輛間距下，不同車輛數(shù)對橋梁跨中截面豎向位移的影響。結果表明:橋梁跨中最大豎向位移隨車輛數(shù)增加而逐步增大，但車隊中車輛數(shù)達到極值點時，橋梁跨中最大豎向位移不再增加，其主要原因橋梁阻尼系統(tǒng)對結構能量的耗散，與新駛入車輛對橋梁振動相互疊加，達到動態(tài)平衡。

(4)通過計算不同間距比和車輛作用橋梁時，跨中截面沖擊系數(shù)變化范圍，并與多國規(guī)范值進行比較，得出在多車激勵作用橋梁時，德國規(guī)范和中國規(guī)范的沖擊系數(shù)偏于不安全，其他規(guī)范相對安全，建議在后續(xù)分析中，綜合考慮多車激勵的影響，相關研究成果可為公路橋梁多車車橋耦合分析研究提供參考。