基于MASTA的圓錐滾子軸承的低成本滾子母線設計

王修坤, 劉飛濤

（上海汽車集團股份有限公司 技術中心, 上海 201804）

1 前言

圓錐滾子軸承因能夠承受軸向和徑向的組合載荷、且預緊后軸系剛度好，被廣泛應用于汽車變速箱承受重載的位置上。圓錐滾子軸承的滾子母線形狀對于圓錐滾子軸承內部的應力分布及使用壽命具有重要影響。滾子母線是直線的圓錐滾子軸承在實際應用和理論分析中，已經被證明是不可取的，其受到載荷后滾子邊緣和滾道之間有一個彈性趨近量，這個彈性趨近量使滾道靠近滾子端部的區域被拉伸，使滾子端部發生應力集中。滾子沿軸向的應力呈現啞鈴形，即所謂的“邊緣效應”[1-2]。“邊緣效應”導致滾子端部接觸應力飆升，而軸承的壽命和滾子接觸應力的 7次方成反比[3]。“邊緣效應”產生的高應力會使滾道邊緣提前發生疲勞、剝落，剝落隨后向滾道中央迅速擴展，使軸承發生早期失效，降低軸承的旋轉精度和使用壽命，并引發整車 NVH 問題。

為克服滾子的“邊緣效應”，將直線型母線修改為曲線型母線是根本思路，這是因為經過優化設計的曲線型滾子母線可以改善滾子和滾道之間的應力分布、避免發生應力集中。除此之外，曲線型滾子還能改善滾子和滾道的潤滑條件，也能改善由于軸承安裝、加工誤差和軸系工作時撓曲而發生的滾子偏載問題。Lundberg[4]使用解析法建立了對數母線公式，基于此公式中的母線形狀，滾子可以獲得理論上均勻的矩形接觸痕跡。P. M. Johns 和 R. Gohar[5]在 Lundberg 公式基礎上增加了滾子接觸痕跡的半長和半寬尺寸，建立了理論上更為合理的對數母線公式。日本 NTN 的Hiroki FUJIWARA[6]和 Tatsuo KAWASE 進一步優化出可以考慮滾子偏轉的對數母線公式。

計算機技術的進展，使數值分析法優化設計滾子母線變得更加便捷。馬家駒[7]基于影響系數法分析了直線型、圓弧型、圓弧-直線型、對數型和直線加對數型滾子修形曲線在均勻載荷下滾子的應力分布。夏新濤[8]等采用 ANSYS 軟件分析了滾子凸度偏移對于滾子應力分析的影響。圓弧型和對數型母線都能很好地解決滾子的“邊緣效應”問題。

現行的滾子凸度加工工藝主要有貫穿磨削法和貫穿超精法[9-10]，前者在普通無心磨床[11]上用特制砂輪和特制導輪，引導滾子以一曲線的軌跡通過磨削區，獲得滾子修形曲線；后者主要通過雙導輥引導和油石精研的方法獲得修形曲線[12]，前者的機床成本和工藝難度都要低于后者。據滾子加工供應商的統計，加工高精度的對數型母線的機床成本是加工圓弧型母線機床成本的三倍以上。因此，從技術經濟性的角度考慮，本文研究汽車變速器中圓錐滾子軸承的圓弧型和圓弧-直線型滾子的優化設計。

MASTA 是由英國 SMT 公司開發的一款基于the Microsoft.NET 架構建立的齒軸系統開發工具，可以完成齒軸系統的設計計算和分析。軸承滾子凸度設計和分析是 MASTA 的重要功能。MASTA 的操作界面友好，可以快速完成軸承滾子母線的設計，但尚未有文獻介紹，本文基于 MASTA 10.2版本的計算分析功能，以某款手動變速箱中間軸上后端圓錐滾子軸承的滾子母線優化問題為例，用正交試驗法優化出合理的滾子母線形狀。

2 建模

2.1 基于 MASTA 建立變速箱計算分析模型

圖 1 是以一款五速手動變速箱為例，使用MASTA 建立的變速箱計算分析模型。輸入軸兩端依靠球軸承支撐，中間軸兩端依靠圓錐滾子軸承支撐，圖 1 中框選的即為本次分析的圓錐滾子軸承，其標準代號為 30205，具體參數見表 1。

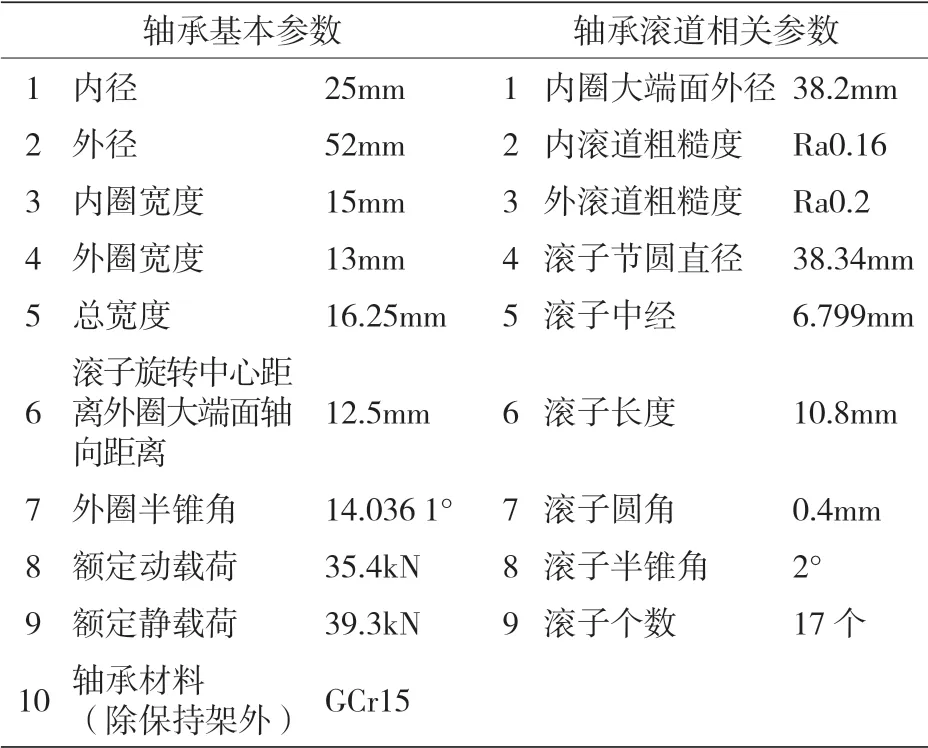
表1 軸承的結構參數

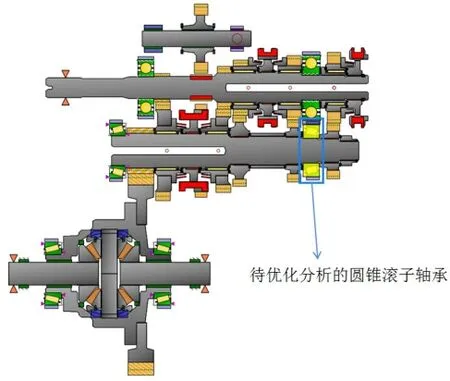
圖1 使用MASTA建立的變速箱二維剖面圖

為保證各個樣本分析計算的一致性，本次計算中的軸承的預緊均為 0，且分析的工況都是軸承最大受力的工況。當滾子母線為直線時，受力最大的滾子在發動機滿扭下的應力曲線如圖 2 所示。由下圖看出，除滾子兩端區域外，滾子在軸向方向受力很不均勻，靠近滾子小端的應力大，靠近滾子大端的應力小，且呈線性遞減。在滾子兩端區域內，發生了嚴重的“邊緣效應”， 最大邊緣應力已經達到 4 000MPa，達到了滾子的應力極限。

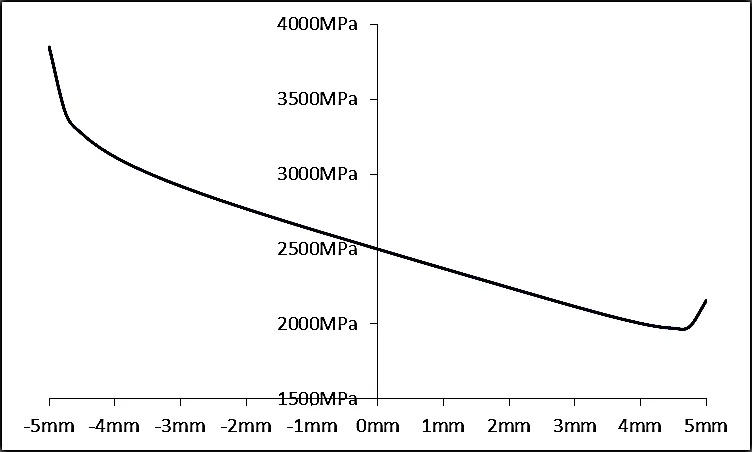
圖2 承受最大載荷的滾子沿軸向的應力分布

2.2 滾子的兩種圓弧類修形

滾子的圓弧修形曲線分為兩種，一種是將滾子母線修為圓弧形，即為純圓弧修形；另一種是將滾子母線修為中間呈直線，兩端是圓弧的修形方式，即為圓弧-直線修形。

2.2.1 純圓弧滾子修形

令滾子母線中點為坐標原點，直線母線為 x軸，垂直于母線且過坐標原點的直線為 y 軸，那么第一種圓弧形的曲線公式如式（1）所示：

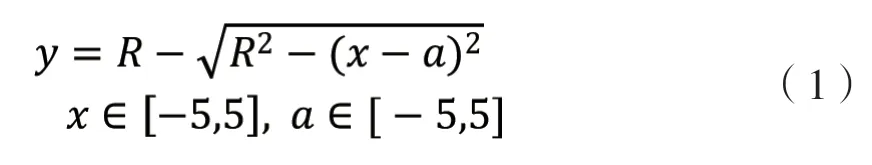
其中，R 表示圓弧修形的圓弧半徑，a 表示圓心距離滾子中心截面的距離，圖 3 是去除滾子兩端倒角后，當圓弧半徑為 2 000mm、a = 2mm時的修形母線。

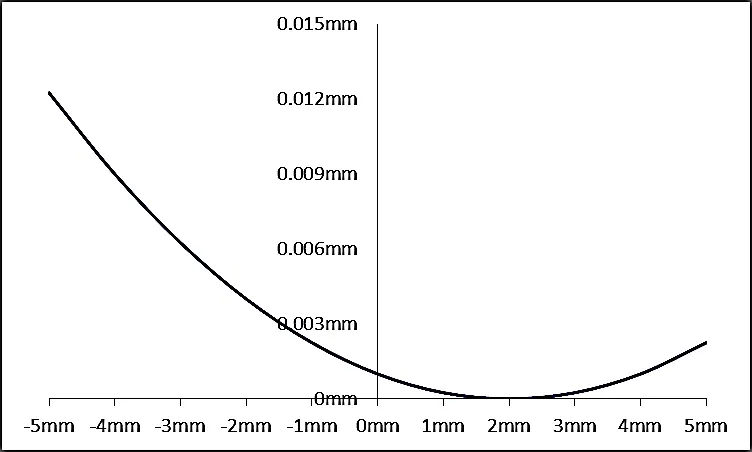
圖3 純圓弧型滾子母線輪廓

2.2.2 圓弧-直線滾子修形

第二種修形方式是將滾子兩端修形為圓弧，中間修形為直線，其修形曲線部分公式：

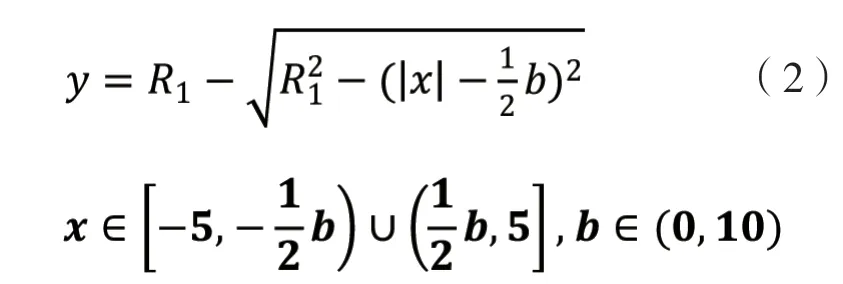
直線部分公式：

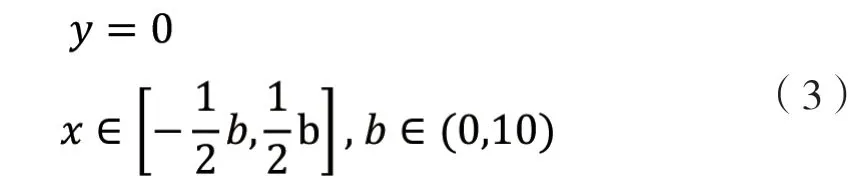
當滾子中直線段長度為 4，圓弧直徑為 2 000mm 時的完整修形曲線如圖 4 所示：

圖4 圓弧-直線滾子母線輪廓

根據解析幾何的相關知識，公式（1）、公式（2）和公式（3）可以統一為下面的公式：

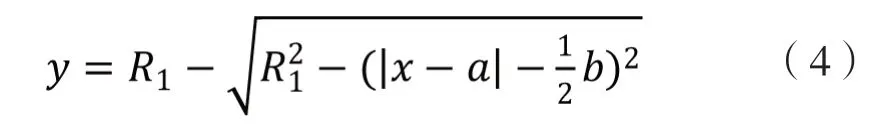
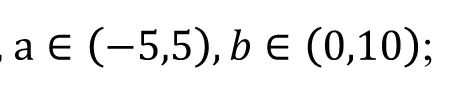
3 分析

為便于分析，將17 粒滾子按照角度從小到大、逆時針的順序排列，并將第 5 號滾子放在90°的位置上，如圖 5 所示：

圖5 軸承滾子的序號定義

當滾子無修形時，即滾子母線為直線時，各個滾子最大應力如圖 6 曲線所示，當滾子母線為直線時，5 號滾子受到的應力最大、載荷最大，最大應力為 4 019.520 1MPa。

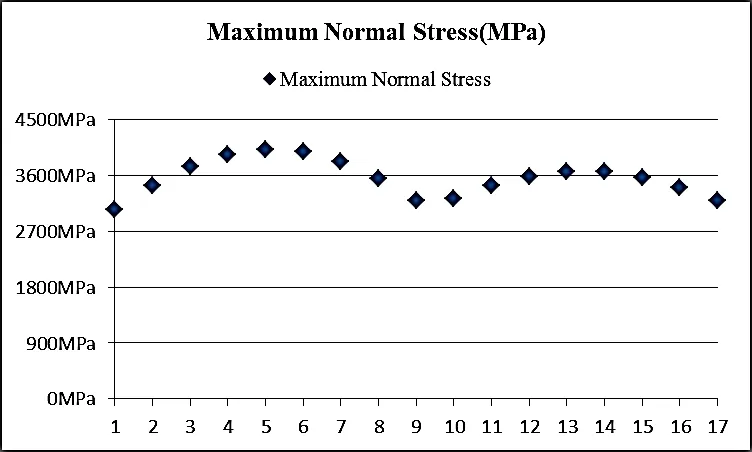
圖6 各個滾子的最大應力

考慮到各個滾子的載荷和應力大小不同，因此本文將所有滾子中受力最大的滾子的應力作為評價滾子修形曲線優劣的標準。

3.1 純圓弧型修形曲線的應力分析

根據公式（1）中展示的函數關系，影響滾子修形母線的因素只有圓弧半徑 R 和母線中心偏移量 a，根據實際的常用工藝參數，將滾子修形母線圓弧半徑和母線中心兩個因素各取五個水平，分析的因素和水平如表 2 所示：

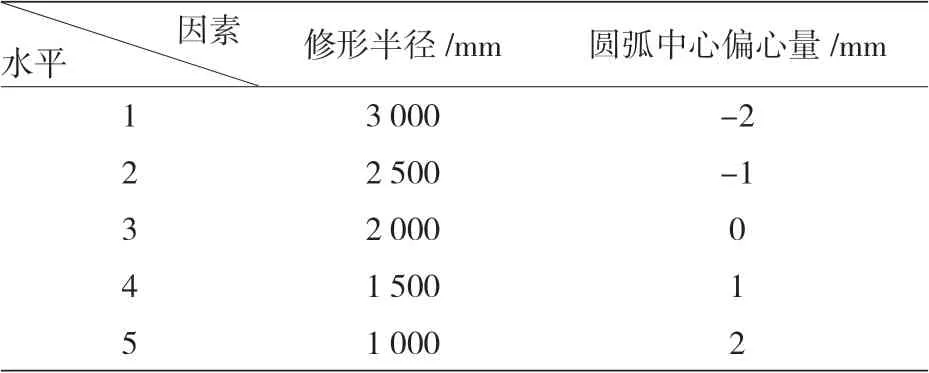
表2 影響純圓弧滾子應力的因素和水平

根據現有兩種因素、五種水平，可以建立如表 3 的全因子分析表格，運用直觀分析的方法，可以發現偏心量對于滾子應力的影響更大：

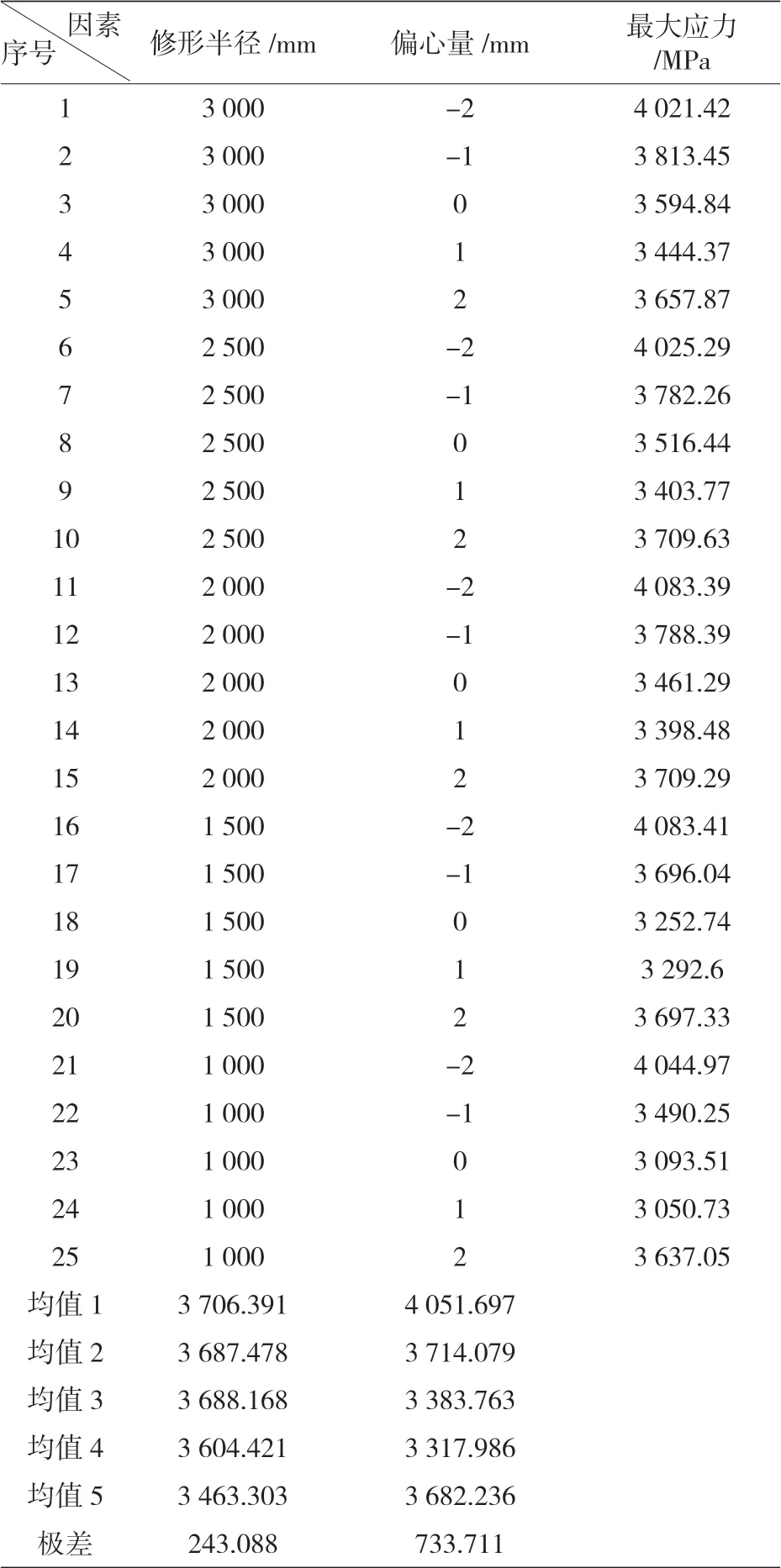
表3 純圓弧滾子應力的全因子水平試驗分析表格

圖 7、圖 8 和圖 9 是根據表中數據繪制的趨勢圖，根據趨勢圖和試驗數據，可以判定偏心量是比圓弧半徑更為重要的影響滾子應力的因素；最優的圓弧半徑是1 000mm，最優的偏心量是1mm。

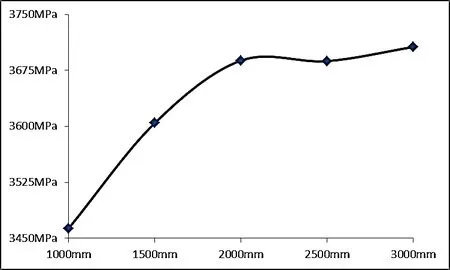
圖7 圓弧半徑對于純圓弧滾子最大應力的影響機制

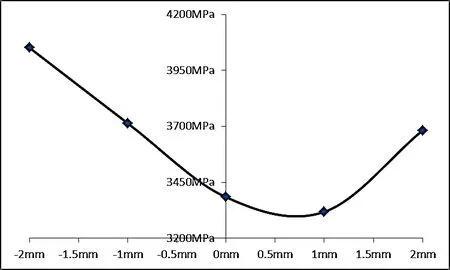
圖8 偏心量對于純圓弧滾子最大應力的影響機制

圖9 表3中25種圓弧母線下各個滾子的最大應力

由圖 7、圖 8 和圖 9 可以看出:

① 隨著圓弧半徑變小，軸承滾子的最大應力下降，且各個滾子的最大應力也趨于更加一致。當偏心量從 0 向 -2 變化時，軸承滾子的最大應力上升；但當偏心量從 1 向 +2 變化時，滾子應力先變小后升高；當偏心量為 +1 時，滾子應力最小。

② 就單個軸承受力而言，17 粒滾子受力呈現雙峰值的特性，即第 5 粒滾子和第 13 粒滾子分別代表上下半圈滾子應力的峰值，滾子應力的優化主要是降低第 5 粒滾子和第 13 粒滾子的應力。

③ 從正交分析的結果可以看出，對于滾子應力大小影響的順序為：圓弧半徑＜圓弧偏心量。

3.2 圓弧-直線型修形曲線的應力分析

為保證所有影響應力變化的因素都能被考慮進凸度修形的優化工作中，同時分析的額數量又盡可能地減少，建立如表 4 的因子水平表格和表 5 的正交分析試驗表格。

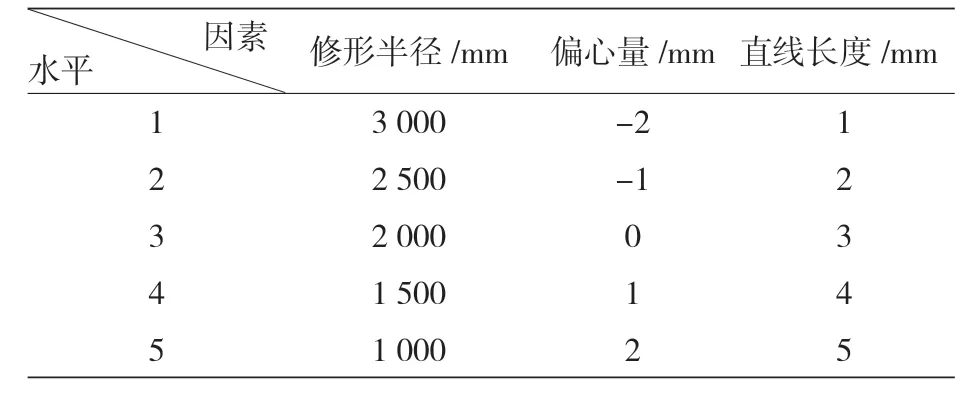
表4 影響圓弧-直線型滾子應力的因素和水平

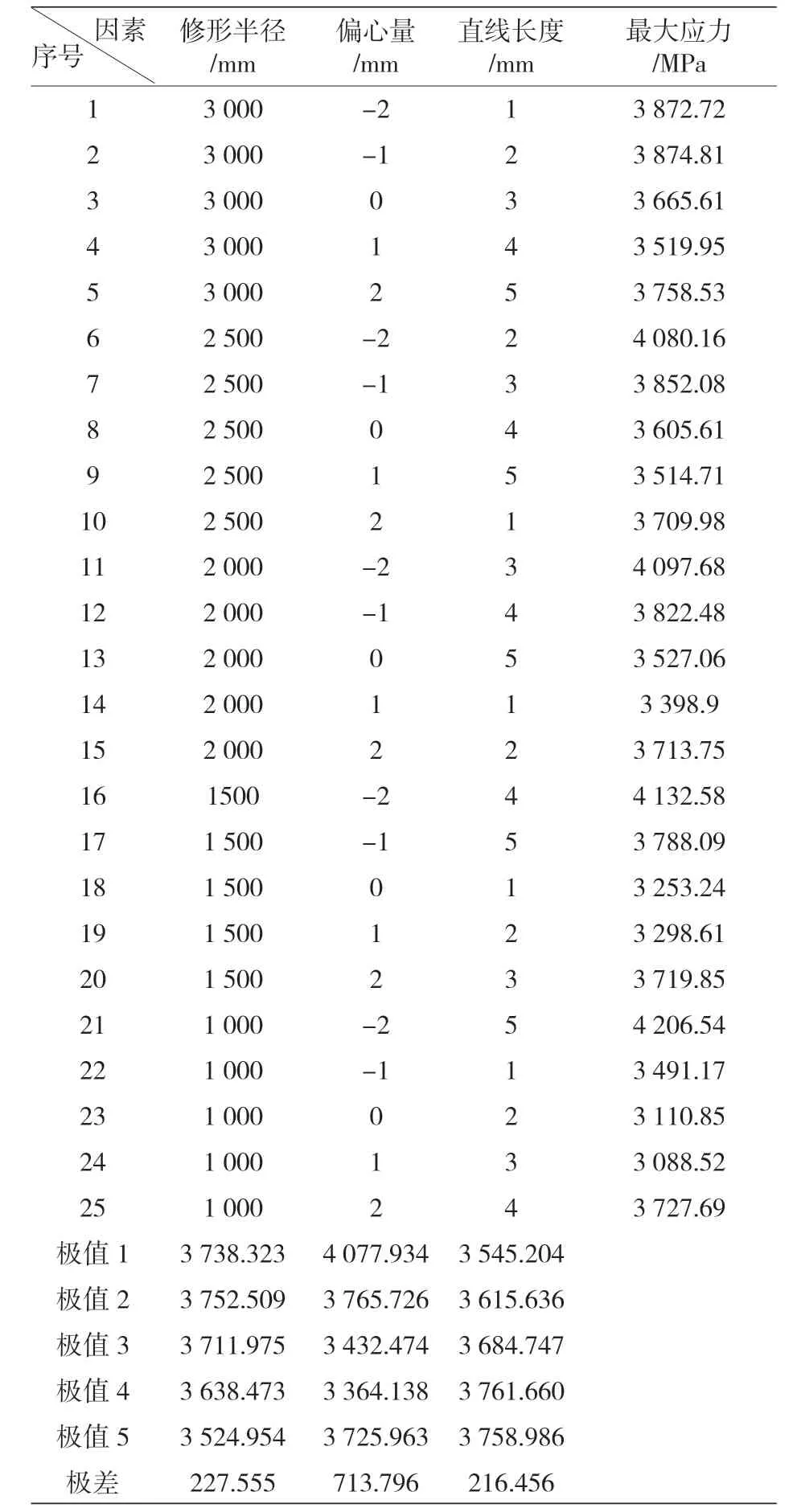
表5 圓弧-直線的正交試驗分析表格

根據表 5 中的數據分析，對于滾子應力影響最大的因素是偏心量，其次是滾子的修形半徑，影響最小的是滾子修形中的直線長度。最優的水平組合是修形半徑為1 000mm、偏心量為1mm、修形直線長度為 1mm。根據上表中數據建立的趨勢分析圖如下所示。

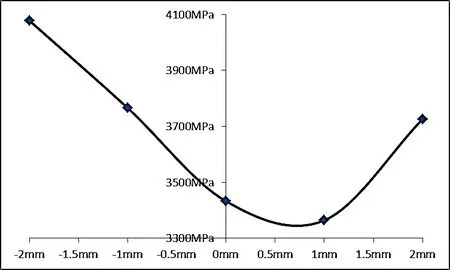
圖11 偏心量對于圓弧-直線型滾子最大應力的影響機制

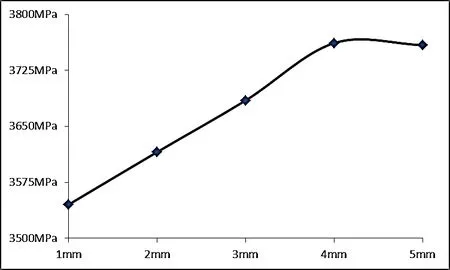
圖12 直線長度對于圓弧-直線型滾子最大應力的影響機制

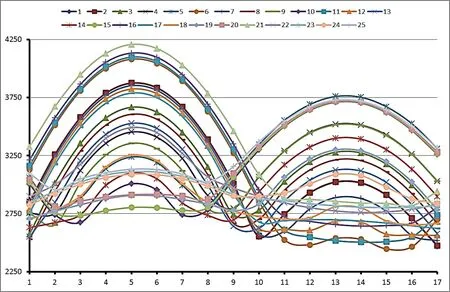
圖13 各種圓弧-直線母線下各個滾子最大應力的情況

針對正交試驗分析的影響，得出圓弧半徑、偏心量和直線長度對于滾子接觸應力的影響機制，從圖 10 ～ 13 可以看出：

圖10 圓弧半徑對于圓弧-直線型滾子最大應力的影響機制

① 增加修形母線中的直線部分前后，圓弧半徑和偏心量對于滾子應力的影響機制不發生變化。

② 就單個軸承受力而言， 17 粒滾子受力呈現雙峰值的特性，即第 5 粒滾子和第 13 粒滾子分別代表上下半圈滾子應力的峰值，滾子應力的優化主要是降低第 5 粒滾子和第 13 粒滾子的應力。

③ 隨著滾子修形圓弧半徑的減小，軸承滾子的最大應力不斷下降，且各個滾子的最大應力也趨于更加一致。從整個試驗來說，隨著修形圓弧半徑的下降，滾子應力下降；當滾子圓弧中心向大端偏 1mm 時，滾子的應力最小，此時向滾子大端或小端偏斜時，應力迅速上升，因此偏心量的合理區間為 [0, 1.5]。

④ 從整體而言，直線段越短，越有利于降低滾子的接觸應力，直線段長度對于軸承滾子應力的影響趨勢和圓弧半徑對于滾子應力的影響趨勢剛好相反。

⑤ 從正交分析的結果可以看出，對于滾子應力大小影響的順序為：圓弧半徑＞圓弧偏心量＞直線長度，其中隨著圓弧半徑變大，應力變大，這是因為圓弧半徑越大，修形量越小；隨著偏心量向右移動，應力變小，因此在實際加工中，應使圓弧中心在 [0, 1] 的范圍內浮動；直線段越長，應力變大，因此實際加工中，應盡量減少直線段的長度。

由上文可知，最優圓弧-直線組合是修形半徑為 1 000mm、偏心量為 1mm、修形直線長度為 1mm，此時計算出的滾子最大應力是 3 052.06MPa，仍略大于純圓弧的最優曲線下的最大應力 3 050.73MPa（基于修形半徑為 1 000mm、偏心量為 1mm 的組合）。可見，純圓弧的滾子母線要優于圓弧-直線的母線。

4 結束語

本文考慮到手動變速箱低成本的特性，將滾子圓弧修形作為改善滾子應力分布的優化目標，使用 MASTA 和正交試驗法作為優化設計工具，找出最優化的圓弧：

① 應優先選擇純圓弧型滾子母線，應盡量降低滾子母線的修形圓弧半徑，最好在 2 000mm以下，偏心量應盡量選擇在 [0, 1.5] 的范圍內。

② 如選擇圓弧-直線型滾子母線，同樣應盡量降低滾子母線的修形圓弧半徑，最好在 2 000mm以下，偏心量應盡量也應選擇在 [0, 1.5] 的范圍內。對于直線段長度，應盡量減少，在 1mm以內為優。