顧及海底地形非線性項的最小二乘配置反演方法

范 雕，李姍姍，歐陽永忠，孟書宇，陳 成，邢志斌，張 馳

1.地理信息工程國家重點實驗室，陜西 西安 710054；2.信息工程大學地理空間信息學院，河南 鄭州 450001；3.南京信息工程大學遙感與測繪工程學院，南京 210044；4.32022部隊，湖北 武漢 430074；5.海軍工程大學導航工程系，湖北 武漢 430074；6.航天工程大學，北京 102206

21世紀是海洋的世紀，海洋是我國經濟社會發展的重要的戰略空間，在國家政治、經濟、科技、軍事發展的全局中日益突出。海洋測繪是實施國家海洋戰略的前瞻性、基礎性、公益性事業，是海洋開發管理、權益維護、科學研究和國防安全等的重要基礎。目前海洋測繪已經成為我國推進科技興海，壯大海洋經濟，建設海洋強國不可或缺的技術支撐[1]。

作為海洋測繪的重要內容，海底地形測量繪制的全球海底地形圖在科學研究、國民經濟和國防建設等方面占據著極其重要的位置：從科學層面，海底地形在很大程度上反映了潛在的地質作用[2]，影響海嘯波的傳播和相關海嘯模型的建立[3]，以及海洋環流等的相關研究[4]；從應用層面，海底地形圖的繪制不僅可保障航道與航運安全，也可為深海潛器的地形輔助慣性匹配導航提供先驗的背景場模型，為深海多傳感器組合精確導航提供又一種可選擇的技術手段。

目前，基礎水深數據獲取技術主要包括船基聲吶測深技術、機載激光雷達測量技術(airborne LiDAR bathymetry)、海岸帶一體化地形測量技術、潛基海底地形測量技術等。然而，上述海深測量手段相對全球海洋而言，不僅測區范圍有限、測量效率較低，而且測量結果數據分布很不均勻。特別是隨著海洋測繪工作測量范圍從近海淺水區向大洋深水區不斷發展，囿于測量平臺限制，船基和潛基測量方式將難以有效滿足遠洋全球測繪需求。采用船基深海測繪將花費200多船年(ship-years)時間，耗費大量人力物力才能繪制完成[5]。

隨著空間對地觀測技術的發展，目前衛星測高技術已成為獲取全球海洋觀測信息的主要手段之一，依托測高衛星獲取的全球海面高數據可恢復全球海洋重力場信息。根據地殼均衡理論，海底地形起伏及其均衡補償物質的密度異常分布將會引起海面重力場的變化，這意味著海面重力場信息與海底地形在一定程度上具有某種對應的相關性關系，它們之間的相關性關系使得利用地球重力場構建深海海域大尺度的海底地形成為可能。利用海面重力場信息反演海底地形，國內外學者提出并驗證了多種反演算法，如重力地質方法[6-8]、SAS方法[9,10]、導納函數方法[11-13]等。其中，基于Parker公式[14]的導納函數方法是依據地形求解重力場級數形式的線性反解，該反演算法涉及諸多地球物理參數求解(準確的地球物理參數對反演結果影響明顯)。SAS方法基于導納函數理論研究了反演波段海底地形和重力數據線性比例關系，進而獲取地形-重力比例因子，巧妙地回避了導納函數方法中地球物理參數的求解難題[15]。文獻[16—17]引入回歸分析技術改進了SAS方法比例因子解算流程，取得了良好的計算效果。然而，無論是SAS方法和回歸分析方法，還是導納函數方法均回避了非線性項對反演結果的影響，僅僅考慮了海底地形和海面重力信息之間的線性成分，因而必定會影響最終反演結果的準確性。關于海底地形反演高次項問題，國內外學者也進行了多方面嘗試。文獻[18]在顧及地殼撓曲均衡狀態下，利用衛星測高重力異常、大地水準面高、船測水深等數據(考慮輸入數據誤差影響)，在空域上利用最小二乘迭代反演方法并顧及高次項影響進行了模擬仿真試驗。文獻[19]依據衛星測高重力異常數據、船測重力異常數據和船測水深數據，采用非線性最小二乘反演技術構建了新西蘭海域考慮高次項影響的海底地形模型(稱為RW99模型)；然而空域最小二乘迭代方法涉及非線性算子求解等，過程復雜、煩瑣且計算效率很低。文獻[20]以航空重力梯度數據為輸入，采用SA(simulated annealing)方法嘗試解決高次項問題，但是SA方法需不斷調整和完善函數參數方可獲得目標函數全局最優解，計算速度十分有限，不利于推廣應用。文獻[21]運用頻率域迭代方法在中國南海部分海域開展試驗，探索解決反演高次項難題的途徑和手段，該方法計算效率高，并取得了較好的試驗效果。

綜上所述，針對目前反演方法常未顧及非線性項影響和目前反演高次項研究進展，本文提出了顧及海底地形非線性項的最小二乘配置(least-squares collocation，LSC)反演方法。首先，利用Earth2014地形位模型研究目標海區地形統計特征，進而解算目標海區局部協方差函數最佳參數；爾后，基于局部最佳協方差函數解算相關信號的自協方差矩陣和互協方差矩陣。然后，以衛星測高重力異常和重力異常垂直梯度為輸入，采用最小二乘配置技術構建兼顧海底地形和海面重力線性趨勢項和非線性項影響的海底地形模型。最后，將反演模型與國際廣泛使用的S&S V18.1和ETOPO1等海深模型進行比對分析，同時引入功率譜密度和相干性等指標評估反演海深模型效能。

1 原理與方法

1.1 最小二乘配置原理

依據Parker公式[14]，海底地形與海面重力異常頻率域的表達式為

F(Δg(x,y))=2πG(ρc-ρw)e-2πf·d·

(1)

F(Δgz(x,y))=2πG(ρc-ρw)e-2πf·d·

(2)

式中，F(Δgz(x,y))表示重力異常垂直梯度Δgz(x,y)的傅里葉變換，其余參數意義同上。當僅考慮式(1)和式(2)中線性項影響時，即所謂重力導納函數

(3)

由式(3)可知，當僅考慮式(1)和式(2)中的線性項影響時，重力異常和重力異常垂直梯度經向下延拓等處理后與海底地形呈線性關系。文獻[16]基于此線性關系，采用回歸分析方法推估相應波段的海底地形

(4)

式中，α、αz和β、βz分別表示線性回歸的比例因子和常數項。據以上分析可知，式(4)算法模型實質是式(1)和式(2)的線性近似，忽略了算法中非線性項影響。然而，文獻[23]和筆者前期研究表明，雖然式(1)和式(2)線性部分對海面重力信息貢獻占主要，但是直接忽略非線性項的貢獻勢必造成有效信息的浪費，特別在地形起伏較大的區域，地形高次項對海面重力信息貢獻明顯。借鑒最小二乘配置理論基本原則，將式(1)和式(2)中級數形式分為線性和非線性兩部分：線性部分表示函數模型系統性參數，是結果的主要影響部分，稱為整個算法模型的趨勢項部分；非線性項部分代表函數模型隨機性參數，為整個算法模型的信號部分，反映與趨勢不符的小的變化，即扣除趨勢項后的殘余項部分，如圖1所示。

圖1 最小二乘配置Fig.1 Least square collocation

圖1中圓點表示觀測值L，實線表示經回歸分析處理后得到的觀測值擬合直線，為觀測值的趨勢項部分，簡稱為AX；曲線為顧及觀測值與趨勢項AX不符的小的變化而擬合生成的曲線，曲線函數表達式為AX+BY，其中BY代表與趨勢項不符的小的變化。顯然，當顧及與趨勢項不符的小的變化時生成的曲線將更加合理。基于以上分析，引入最小二乘配置理論中信號部分，則式(4)表示為

(5)

式中，s表示函數模型的信號部分，代表函數模型非線性項(可認為是扣除趨勢項后的殘余地形部分)對結果影響，從而依據式(5)可實現對線性模型的修正和完善。式(5)觀測方程的矩陣形式為

L=AX+s+Δ

(6)

式中，L為海底地形觀測值向量；A為系數矩陣；X表示參數矩陣；s為信號向量；Δ表示觀測值誤差向量，各量具體形式為

(7)

將式(6)表示為最小二乘配置的函數模型為

L=AX+BY+Δ

(8)

式中，B和Y具體表達式為

(9)

式中，In為n階單位陣；S代表顯信號(已測點殘余地形信號)；S′表示隱信號(未測點殘余地形信號)。式(8)對應的誤差方程為

(10)

最終，式(10)最小二乘配置解為

(11)

式中，C表示相應的協方差矩陣，如CL和Css分別代表觀測值和顯信號的協方差矩陣。

1.2 局部地形協方差函數

協方差函數是有效實施統計分析的基本依據，合理的協方差函數應充分反映區域數據的變化規律和相關性，良好的協方差函數能得到較好的計算結果；反之，若協方差函數并非區域數據的有效表征，則將會歪曲解算結果。因此確定協方差函數之于最小二乘配置尤為重要。囿于客觀原因限制，通常依托經驗協方差函數獲取區域協方差矩陣。設距離為l，從數學角度分析可知，經驗協方差函數為相關函數，同時應滿足以下3條規則[24]：①距離l為零時，相關性為正，C(0)=C0>0；②協方差函數為偶函數，C(-l)=C(l)；③距離l為零時，相關性最強，C(0)≥C(l)，當且僅當l=0時，等號成立。同時滿足以上3個條件的協方差函數為強相關協方差函數。本文選擇以下強相關協方差函數作為經驗協方差函數。

(1)Moritz協方差函數

(12)

(2)Inverse協方差函數

(13)

(3)Gauss協方差函數

C(l)=C0·e-a2l2

(14)

式中，C0是兩點距離為零對應的協方差函數值，表示協方差函數的變化幅度；l為兩點之間距離；a為常數。

綜上，利用研究海域離散海深測量數據、衛星測高重力異常數據和重力異常垂直梯度數據，采用最小二乘配置技術構建海底地形格網數值模型步驟可概括為：

(1)獲取海底地形反演波段范圍。依據設計的高通、低通濾波器和撓曲波長、海區海深內在聯系，結合海底地形影響重力信息有限波段特點和先期研究成果，確定研究海域利用重力數據反演海底地形有效波段范圍。

(2)獲取殘余海底地形信息。依托先驗海底地形模型和衛星測高重力異常數據，采用最小二乘技術獲得地形與重力數據趨勢項信息，然后扣除先驗海底地形模型中地形與重力趨勢項部分，進而獲取殘余海底地形信息。

(3)確定目標海區局部協方差函數。研究分析目標海域殘余海底地形統計特征，依據最小二乘擬合方法解算局部協方差函數未知參數，從而得到能夠較好反映目標海域地形特征的局部協方差函數，進而獲取相關信號的自協方差矩陣和互協方差矩陣。

(4)獲取反演波段重力信息和非反演波段海底地形。利用設計的高通、低通和帶通濾波器對系統輸入數據(離散船測點和重力數據)實施濾波操作，得到相應波段的重力和海底地形信息。

(5)海底地形數值模型構建。利用獲取的研究海域信號協方差矩陣以及反演波段輸入數據信息，采用最小配置方法構建反演波段海底地形；然后疊加反演波段和非反演波段海底地形，進而得到最終海底地形數值模型。

基于以上分析，利用稀疏船測數據、衛星測高重力異常和重力異常垂直梯度數據，采用最小二乘配置技術構建海底地形格網數值模型整體設計路線如圖2所示。

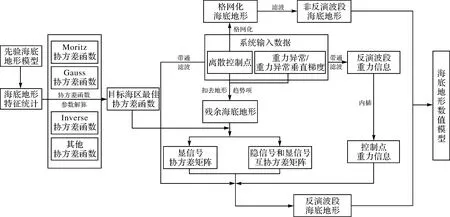
圖2 最小二乘配置路線Fig.2 Inversion scheme of least square collocation

2 數值試驗分析

2.1 數據準備與前期處理

選擇日本海某1°×1°(133.5°E—134.5°E，38°N—39°N)海域開展研究試算工作，其中數據來源如下：

(1)衛星測高重力數據(包括重力異常和重力異常垂直梯度數據)來源于SIO，UCSD(Scripps Institution of Oceanography,University of California,San Diego)，V24.1版本，分辨率為1′，衛星測高重力資料統計結果見表1。

表1 研究海域重力數據統計Tab.1 Gravity data statistics of the research sea area

(2)研究海域船測多波束和單波束數據來源于NGDC(The National Geophysical Data Center)發布的研究海區實測數據，共收集到研究海域2228個船測數據。

依托船基方式利用聲學測量儀器對研究海域實施點、線和面測量，囿于導航條件和儀器等方面因素影響，原始海深測量結果中難免存在粗差。因此本文采用S&S V18.1海深模型作為先驗海深模型對原始海深測量數據進行質量控制：

(1)采用雙線性插值技術將S&S V18.1海深模型值內插到原始海深測量點處得到模型內插值。

(2)將模型內插值與原始海深測量值作差得到海深殘差值。

(3)將3倍殘差標準差設置為閾值，把海深殘差絕對值大于閾值的船測點予以剔除，從而得到經3σ原則簡單處理后的海深數據。

原始海深數據、海深殘差和處理后的海深數據統計結果見表2，其中括號內為船測海深點數。

表2 海深數據統計結果Tab.2 Statistical results of bathymetric data m

由表2可知，海深殘差值標準差為88.09 m，從而剔除粗差的閾值設置為264.27 m。最終剔除了67個粗差可疑點，占船測點總數的3%左右，得到2161個船測數據。依據前期研究可知，重力異常或者重力異常垂直梯度長波段信號主要受地殼均衡影響，短波段高頻重力信息受向下延拓因子和觀測噪聲影響嚴重[25]，因此利用重力異常或者重力異常垂直梯度數據僅可恢復有限波段海底地形信息，非反演波段地形信息通常采用船測海深數據恢復[10-11,15,26-28]。據此，從2161個船測數據中隨機挑選1659個數據作為控制點，用于補償非反演波段海底地形信息，控制點個數約占總測深點數的76.77%；剩余502個船測點作為評價最終海深模型構建的檢核點待用。研究海域控制點和檢核點空間分布如圖3所示，其中白色六邊形表示控制點，黑色三角形代表模型評估待用的檢核點，背景圖為S&S V18.1海深模型。

2.2 輸入數據濾波

分別選擇合適的高通和低通濾波器對重力數據進行濾波處理，以抑制重力數據長波和短波部分信息對海底地形反演結果的影響。選擇的高通濾波器和低通濾波器為

(15)

式中，τ和ζ為濾波參數。高通濾波器W1(fx,fy)可有效去除長波段信號的影響。SIO學者在利用SIOV20.1重力異常數據構建S&S V15.1海深模型過程中，取參數ζ=3891 km4參與數據濾波計算，不同平均海深d對應的低通濾波器和不同波長對應的低通濾波器(1-W1(fx,fy))形狀分別如圖4(a)實線和虛線所示。

圖3 控制點和檢核點分布Fig.3 The distribution of control points and checkpoints

地殼均衡補償將地殼描述為漂浮在流體巖漿表面的彈性薄板，具備抵抗地質載荷導致薄板產生形變的能力。也就是說，地殼彈性厚度類似低通濾波器能夠抵消短波段地質體影響。當地形波長較長超過彈性板能夠抵消波長的極限，彈性板將發生形變，產生地殼均衡補償效應。彈性板能夠抵抗的地形極限波長值，稱為撓曲波長。不同厚度的彈性板對應不同的撓曲波長，而利用重力數據反演海底地形需盡量抑制地殼均衡補償對地形-重力信息的干擾，盡量使用重力信息中的地形“成分”。綜合均衡響應函數[25]和式(15)可得不同彈性厚度對應撓曲波長如圖4(b)所示。有效彈性厚度分別為3、5、10和15 km時，對應的發生撓曲補償現象的波長為120、160、200和250 km。

因研究海區平均海深為1.31 km(船測海深平均值)，由圖4(a)低通濾波器與海深和濾波波長的關系可得濾波波長范圍大約在10～13 km，結合文獻[15]和文獻[29]最終短波段截斷波長選擇為15 km。另外為有效抑制地殼均衡補償對海面重力信息的影響，充分利用衛星測高重力信息中的地形分量，依據文獻[30]認為研究海域有效彈性厚度為5 km，然后根據有效彈性厚度與波長的關系(圖4(b))，長波段截斷波長最終選擇為160 km。從而試驗海域利用衛星測高重力數據反演海底地形的反演波段范圍為15～160 km。采用合適的帶通濾波器(式(15)高通濾波器和低通濾波器乘積)獲得的反演波段重力數據數值統計結果見表3。

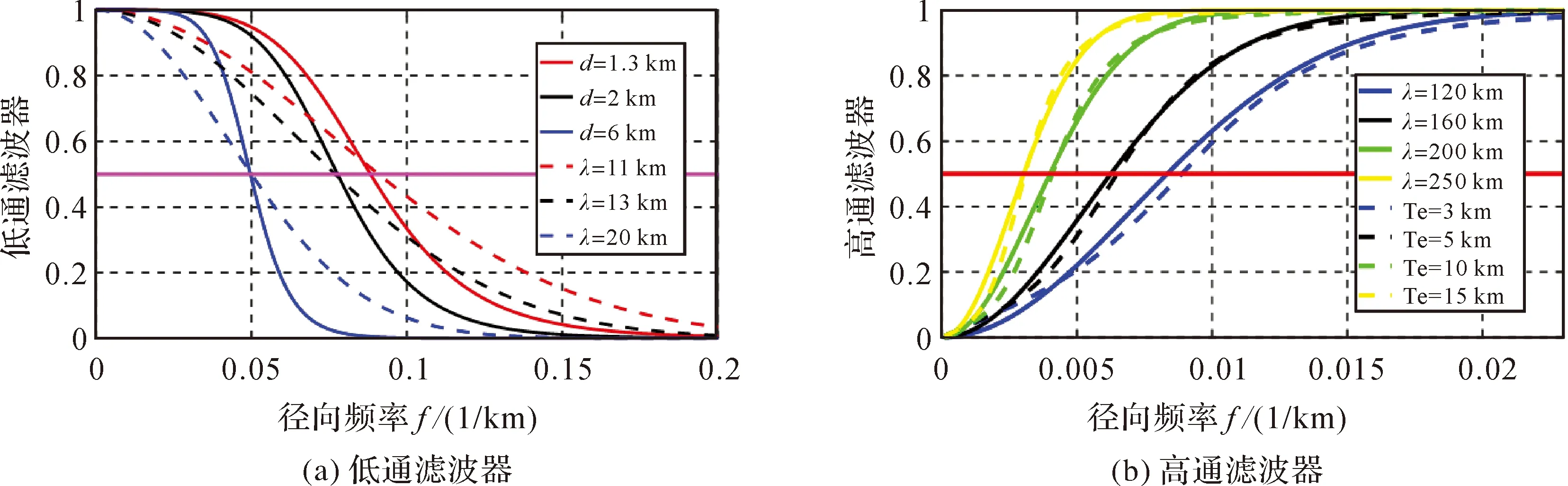
圖4 濾波器Fig.4 Filter

表3 反演波段重力數據統計Tab.3 Statistics of gravity data of inversion waveband

2.3 選取協方差函數

利用研究海域稀疏離散控制點和相關重力場信息，基于最小配置方法構建海底地形格網數值模型過程中，待求隱信號為格網海底地形值趨勢項的小變化，顯信號是控制點殘余海底地形信息(扣除趨勢項)。依據最小二乘配置理論可知，信號與觀測值間通過協方差函數相聯系，合理的協方差函數一直是最小二乘配置中的關鍵問題。因研究對象的幾何和物理特性決定了其內部相關性，從而確定協方差函數時，需充分考慮這些特性以正確反映研究對象的這種相關性。

據此，本文選擇Earth2014地形模型[31]作為先驗海底地形模型統計分析目標海域空間屬性特征，基于對研究海域海底地形特征的充分描述和表達，從而解算協方差函數的合理參數以獲取研究海域相關量的協方差矩陣。Earth2014為WAGG(Western Australian Geodesy Group)發布的一套球諧系數模型，包括全球地形(Earth’s topography)、巖石等效地形(rock-equivalent topography)、地球形狀(Earth’s shape)和地形位模型(implied topographic potential)。Earth2014格網數據包含1′和5′兩個分辨率版本，球諧系數(spherical harmonic coefficients)最高階次為10 800階。構建Earth2014系列模型數據來源如下：

(1)南極洲基巖(bedrock)、冰厚(ice thickness)和海深數據來源于Bedmap2，如圖5暗紅色區域所示。

(2)格林蘭基巖地形數據(bedrock topography)由GBT(Greenland Bed Topography)V3提供，如圖5紅色區域所示。

(3)海洋、主要內陸湖泊和北半球高緯度陸地地形(除格林蘭外)數據源自SRTM30_PLUS V9，對應圖5藍色區域和黑色區域。

(4)緯度±60°之間的所有陸地數據來自于SRTM V4.1 Topography，對應圖5黃色區域。

from http:∥ddfe.curtin.edu.au/圖5 Earth2014輸入數據空間分布Fig.5 Distribution of data in Earth2014

Bedmap2、GBTV3、SRTM30_PLUS V9和SRTM V4.1數據融合過程詳見文獻[31]。最終，Earth2014提供了地球上主要冰蓋(ice sheet)最新的基巖和地形信息以及海洋深度格網信息。同時為滿足不同應用需求，Earth2014模型包括如下幾個類型：①地球物理表面(the physical surface，SUR)；②基巖(bedrock，BED)，即不考慮地球上水和冰的影響；③地形、基巖和冰(topography bedrock and ice，TBI)，即不考慮地球上水的質量；④冰蓋厚度(ice sheet thickness，ICE)；⑤巖石等效地形(rock-equivalent topography，RET)，即將冰層和水層“壓縮”為等效巖石厚度。根據本文研究需要，選擇BED類型的地形位系數模型，稱為Earth2014.BED2014.1min.geod。利用地形位系數模型求解地形(高度起算面為平均海平面)公式如下

(16)

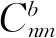
為使研究區域殘余地形統計協方差充分表達研究區域地形特征，需充分且有效地利用研究區域數據。從而利用TEarth2014_Res模型統計研究海域殘余地形協方差時，統計范圍設置為研究區域最大經度縮小20′，最小緯度增大20′所形成的正方形格網，即有效距離最大為40′。基于以上分析，顧及協方差函數非負特點，研究海域共得到殘余地形協方差統計值26組。其中距離為零時，協方差C0為0.043 km2，相關長度為6′左右(C0/2對應的距離)。采用最小二乘方法擬合各個局部協方差函數參數，依據式(12)、式(13)和式(14)可得目標海域Moritz協方差函數、Inverse協方差函數和Gauss協方差函數分別為

(17)

2.4 海底地形模型構建

利用最小二乘配置方法構建海底地形模型中顯信號為控制點反演波段殘余海底地形信息。本文獲取顯信號方法是：將事先挑選的1659個控制點格網化得到格網化海深；然后對格網化海底地形施以帶通濾波操作，進而得到反演波段海底地形信息；憑借SIOV24.1重力異常數據，采用最小二乘配置方法獲得地形和重力異常趨勢項地形信息，進而通過扣除地形趨勢項得到殘余地形；然后采用雙線性插值技術將殘余海底地形內插到控制點處，從而得到控制點殘余海底地形。囿于插值方法限制，若控制點處于邊緣位置將導致插值失敗，因此為保證插值過程順利完成，將控制點范圍沿經度和緯度方向分別內縮2′，最終得到1409個控制點。利用目標海域局部經驗協方差函數(Moritz協方差函數、Inverse協方差函數和Gauss協方差函數)解算得到相應的顯信號協方差矩陣，以及隱信號和顯信號互協方差矩陣。分析易知，當顯信號間距離很近時，對應的協方差矩陣表現極強奇異性，因而為克服顯信號協方差矩陣奇異難題，考慮到研究區域海深測量數據質量，依據S-44(4th)海道測量標準中三等測量估計測量水深精度，當水深d(研究海域平均水深)選擇1 296.40 m時，船測海深觀測精度(協方差)為890.07 m2。借鑒文獻[37—38]的處理方法，將Moritz協方差函數、Inverse協方差函數和Gauss協方差函數解算得到的顯信號協方差矩陣與海深觀測值方差之和代入參與計算。

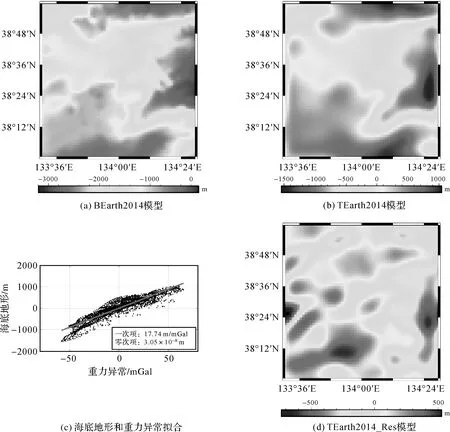
圖6 Earth2014相關模型Fig.6 Earth2014 relevant models

最終以衛星測高重力異常和重力異常垂直梯度數據為數據輸入，基于最小二乘配置技術，分別采用研究海域Moritz協方差函數、Inverse協方差函數和Gauss協方差函數構建的海深模型結果如圖7和圖8所示，分別稱為BAT_DG_Moritz模型、BAT_DG_Inverse模型、BAT_DG_Gauss模型、BAT_VGG_Moritz模型、BAT_VGG_Inverse模型和BAT_VGG_Gauss模型。依據3種協方差函數解算得到的海底地形趨勢項的常數項和一次項參數和利用最小二乘擬合獲得的常數項和一次項參數結果見表4。可以看出，基于Gauss協方差函數計算得到的最小二乘配置方法中趨勢項部分與最小二乘擬合參數差別明顯；Moritz協方差函數和Inverse協方差函數趨勢項解算結果與最小二乘方法解算結果最為接近。利用最小二乘方法計算得到的地形與重力數據(重力異常和重力異常垂直梯度)線性項參數，分別構建相應的海深模型。其中以重力異常為輸入建立的海深模型稱為BAT_DG_LS模型，利用重力異常垂直梯度構建的海深模型稱為BAT_VGG_LS模型，效果如圖9所示。可以看出，利用最小二乘方法構建的海深模型與采用最小二乘配置方法建立的海深模型均能反映研究海域地形概貌，但是與最小二乘配置方法反演的海底地形存在明顯差異，如在研究海域西部兩類模型存在明顯不符。究其原因，最小二乘配置顧及地形和重力二者線性趨勢關系的同時，也包含了對二者線性趨勢變化的反映，結果更加合理可信。

2.5 海底地形模型分析評估

考察評價利用衛星測高重力數據，采用最小二乘配置方法建立的海深模型精度和效能，引入目前國際上廣泛使用的ETOPO1模型、GEBCO模型、SIO系列模型之S&S V18.1模型以及文獻[39]利用重力異常垂直梯度采用SAS(Smith and Sandwell)方法反演的BAT_VGG海深模型參與模型比對評估環節，各海深模型統計結果見表5。由于本文反演模型建立過程中涉及時頻轉換，從而為消除邊緣效應影響，將最終反演結果分別沿經度和緯度方向內縮5′參與統計。

圖7 重力異常構建海深模型結果Fig.7 Bathymetry inversion using gravity anomaly

圖8 重力異常垂直梯度構建海深模型結果Fig.8 Bathymetry inversion using vertical gravity gradient anomaly

圖9 最小二乘方法構建海深結果Fig.9 Bathymetry inversion using least square

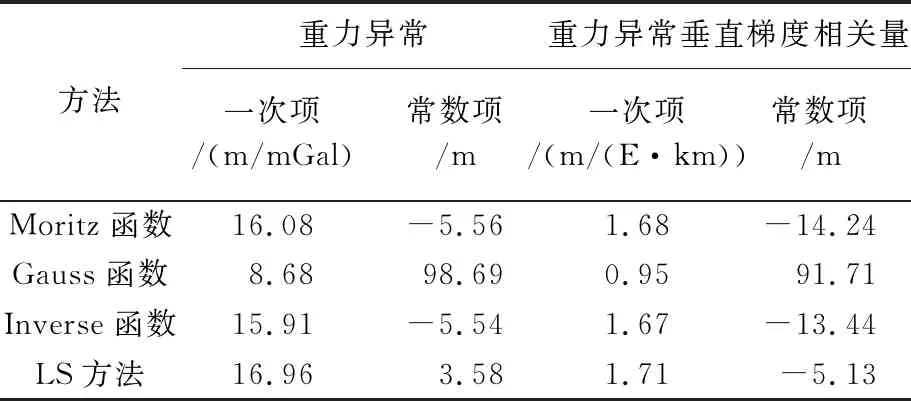
表4 LSC和LS趨向性參數解算結果Tab.4 Parameters of the leaner term calculated by LSC and LS

從表5可以看出，研究海域海深模型中水深最淺約為400 m，最大水深為3000 m左右。以重力異常和重力異常垂直梯度為輸入，采用相同殘余地形協方差函數，依據最小二乘配置方法反演得到的海深模型(如BAT_DG_Moritz和BAT_VGG_Moritz、BAT_DG_Inverse和BAT_VGG_Inverse等)統計參數(最大值、平均值和相關系數等)結果相近，對應的海深模型相關程度高達0.999。以BAT_DG_Gauss和BAT_VGG_Gauss模型為例，兩海深差值最大值、最小值，平均值和標準差分別為33.15、-33.30、-0.61和8.02 m，兩海深模型相關系數高達0.999 9，兩模型表現狀況與采用的反演方法有關。與其余海深模型比對發現，采用最小二乘方法獲取的趨勢項海深模型BAT_VGG_LS和BAT_DG_LS模型最大水深約為2300 m，明顯淺于其余海深模型統計結果；與ETOPO1、GEBCO和S&S V18.1等海深模型相關程度也低于利用最小二乘配置反演海深結果，說明了顧及非線性趨勢項能明顯提高反演模型地形表達效果。海深模型間相關系數顯示，BAT_VGG模型與ETOPO1模型和GEBCO模型相關系數為0.93，ETOPO1模型與GEBCO模型相關系數為0.92左右，而本文采用最小二乘配置方法反演海深模型與其余海深模型相關系數均超過了0.95，進一步說明了本文反演海深模型與目前發布的海深模型均能夠較好附和，驗證了本文反演方法的可行性。以502個檢核點作為外部檢核條件檢驗海深模型精度(海深模型值通過相應的內插函數內插到檢核點處，并與檢核點處實測海深值進行比對)，定義海深模型相對精度為檢核均方差值與檢核點平均海深(取正值)之比，海深模型檢核統計結果見表6。

表6海深模型檢核統計結果顯示，以重力異常為輸入，采用最小配置方法建立的海深模型各統計指標(最大值、最小值和均方差等)結果相近。仔細對比各海深模型檢核統計結果發現，本文最小二配置反演模型檢核平均值絕對值達到了111 m左右，回歸分析方法建立的BAT_DG_LS和BAT_VGG_LS檢核平均值分別約為91和75 m，BAT_VGG模型、ETOPO1模型和GEBCO模型也分別約為50、22和35 m。一般檢核平均值應該在零值附近或量級較小，這時再去考慮其他指標，如標準差和均方差等才更合適。產生該現象(檢核平均值偏離零值較大)的原因，筆者認為是反演模型中存在系統誤差所致，若能有效約束系統誤差影響，則反演模型質量可較大幅度提升，例如文獻[40]利用質量較好的稀疏實測數據對反演模型進行校正，從而削弱了系統誤差的影響。本文采用在海深模型基礎上加上模型檢核平均值的方法以削弱系統誤差影響，削減系統誤差后的各海深模型檢核統計結果見表7，海深模型括號內的數為參與統計的有效檢核點數。需要說明的是，由于檢核統計指標如標準差、均方差等可能受粗差或異常值的影響較大，因此在統計過程中若檢核點差值處于閾值(設置為3倍標準差和平均值之和)之外，則認為是粗差或異常值并予以剔除，例如BAT_DG_Moritz模型和BAT_DG_LS異常值點數分別有15個和4個，有效檢核點分別有487個和498個。

比對表6和表7結果可以發現，各海深模型除去系統差和異常值后統計指標改善明顯。利用最小二乘配置方法反演的海深模型檢核差值平均值由百米量級下降到3 m范圍內；BAT_DG_LS和BAT_VGG_LS檢核差值平均值也分別從91.86 m和74.82 m降低到4.79 m和5.06 m，S&S V18.1模型檢核平均值下降為0.82 m，說明了模型系統誤差得到了有效削弱。系統誤差削弱后，各模型檢核均方差也大幅改善，BAT_DG_Moritz和BAT_VGG_Moritz等采用最小二乘配置建立的海深模型檢核精度從約127 m提高到50 m以內，精度提升達到了2.5倍到4倍左右；而BAT_DG_LS和BAT_VGG_LS扣除系統差和檢核點異常值后，檢核精度提升有限，僅提高了4%左右；BAT_VGG、ETOPO1、GEBCO和S&S V18.1模型檢核精度分別提高33%、15%、10%和34%左右。

表7統計結果顯示，輸入依據為重力異常或者重力異常垂直梯度時，Moritz協方差函數構建的BAT_DG_Moritz模型和BAT_VGG_Moritz模型檢核精度略高于基于Gauss函數和Inverse函數反演得到的海深模型。仔細考察使用不同重力數據和相同協方差函數反演海深檢核統計結果可以發現，采用相同協方差函數反演海深結果中，利用重力異常獲取的海深結果優于重力異常垂直梯度反演海深結果。另外，基于最小二乘配置采用不同重力源構建的海深模型檢核插值與檢核點相關系數均達到了0.99以上，與檢核點相關程度強于ETOPO1、GEBCO和BAT_VGG模型，與S&S V18.1模型相當；同時本文利用最小二乘配置反演海深模型相對精度在3.8%以內，與S&S V18.1模型相當，遠遠優于其余海深模型。

觀察比對本文利用最小二乘方法和最小二配置方法構建的海深模型結果發現，利用最小二乘方法構建的海深模型檢核精度遠低于最小二配置結果，如以重力異常為輸入數據，采用最小二乘方法建立的BAT_DG_LS模型，檢核均方差為171 m左右，而利用最小二乘配置方法構建的海深模型檢核精度最低為50 m左右，相比BAT_DG_LS模型精度提高了2.5倍左右；BAT_VGG_LS模型檢核均方差值為215 m左右，而基于最小二乘配置使用重力異常垂直梯度構建的海深模型檢核精度最低為50 m左右，相比BAT_VGG_LS精度提升了約近3.5倍；同時BAT_DG_LS和BAT_VGG_LS模型不僅檢核差值絕對值最大值均超過了500 m，而且相對精度也均超過了13%。據前計算結果可知，采用Moritz協方差函數和Inverse協方差函數獲取的趨勢項參數與最小二乘方法解算結果較為接近，可是最終反演海深結果中諸多統計指標均遜于最小二乘配置反演海深結果，因此進一步說明了顧及反演算法中非線性項影響的必要性和本文反演方法的有效性。本文利用最小二乘配置反演海深模型的檢核差值標準差在45 m左右，BAT_VGG模型、ETOPO1模型和GEBCO模型檢核標準差均接近或者超過了百米。綜合對比各海深模型，海深模型檢核均方差統計結果中，S&S V18.1模型檢核精度最高，檢核結果為40 m左右，本文利用最小二乘配置構建的海深模型效能與之相當。進一步驗證了反演海底地形時顧及非線性項影響的重要性以及最小二乘配置解決反演非線性問題的有效性。

選擇利用最小二配置方法反演海深檢核精度最高的BAT_DG_Moritz模型和BAT_VGG_Moritz模型參與進一步研究各海深模型在目標海域表現情況，分析不同檢核差值范圍內檢核點占比結果如圖10所示。

從不同檢核差值檢核點數量占比結果(圖10(a))可以看出，S&S V18.1模型、BAT_DG_Moritz、BAT_VGG_Moritz和ETOPO1模型在差值絕對值小于大約50 m以內的檢核點數量占比較多；特別是S&S V18.1模型、BAT_DG_Moritz模型和BAT_VGG_Moritz模型差值小值數量明顯多于其余模型；而本文BAT_DG_Moritz模型和BAT_VGG_Moritz模型又優于S&S V18.1模型；其中，GEBCO模型差值小值數量占比較少。圖10(a)結果還表明，各海深模型檢核差值超過200 m后不同差值對應的檢核點數量已很少。各個海深模型不同檢核差值范圍檢核點占比情況如圖10(b)所示。考察圖10(b)可以發現，BAT_DG_Moritz模型和BAT_VGG_Moritz模型不同檢核差值范圍檢核點比例曲線走勢幾乎一致，導致該現象與最小二乘配置方法本身機理有關。S&S V18.1模型、BAT_DG_Moritz模型和BAT_VGG_Moritz模型在不同檢核差值范圍檢核點比例遠遠高于其余模型；BAT_VGG模型在檢核點比例小于60%左右時，檢核點占比均小于ETOPO1模型；GEOCO模型相對于其余模型表現欠佳，在差值大于150 m左右后，GEOCO模型檢核差值比例與ETOPO1模型近乎一致。檢核點占比80%時，S&S V18.1模型、BAT_DG_Moritz模型和BAT_VGG_Moritz模型檢核差值最大值僅約為42 m，ETOPO1模型和GEBCO約為150 m，BAT_VGG模型約為107 m；檢核差值100 m范圍內BAT_DG_Moritz模型和BAT_VGG_Moritz模型檢核點數量占比約93%，ETOPO1模型約占73%，GEBCO模型約占55%，BAT_VGG模型約占79%，S&S V18.1模型達到了96%左右。由此可見，S&S V18.1模型、BAT_DG_Moritz和BAT_VGG_Moritz模型在目標海域表現最佳，其余海深模型檢核差值絕大多數在200 m范圍內。

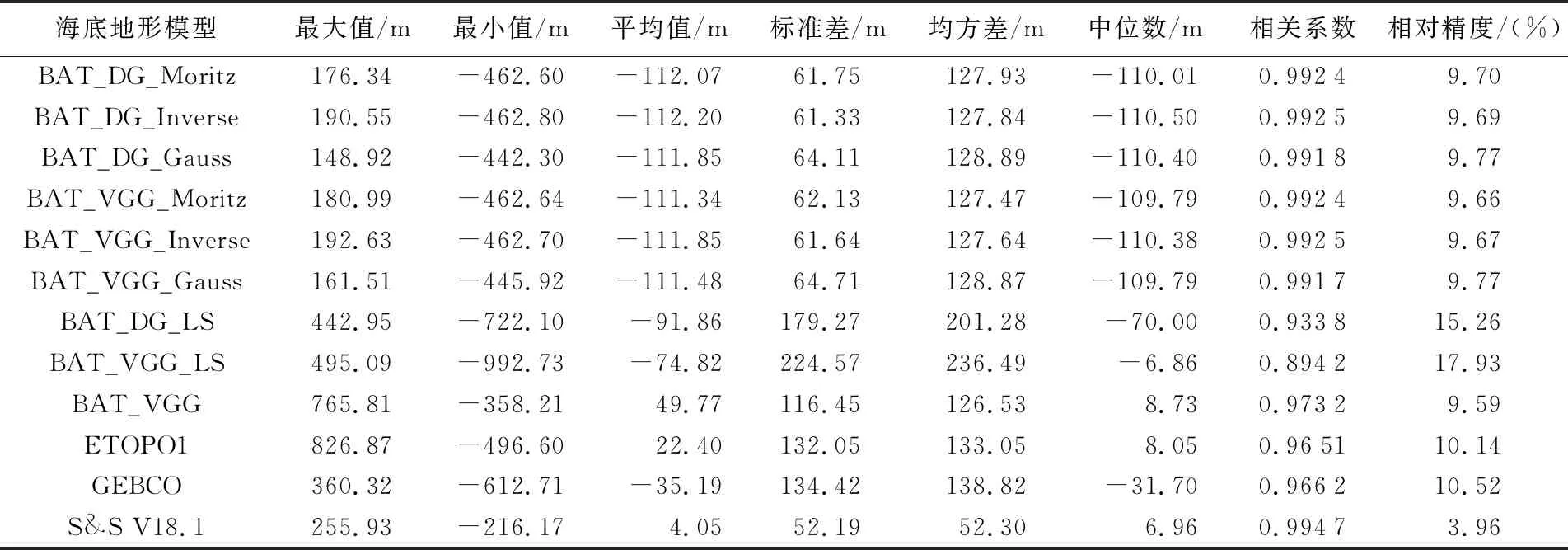
表6 海深模型檢核統計結果Tab.6 Statistical checking results of bathymetry models

表7 海深模型扣除系統誤差后檢核統計結果Tab.7 Statistical checking results of bathymetry models after deducting system errors

圖10 不同差值范圍檢核點數量比例Fig.10 Ratio of checkpoints in different range of difference

導致各海深模型在目標海域表現產生差異的原因，筆者認為主要來自于兩個方面。一是輸入數據源、數據量和數據質量差異，如本文船測海深數據主要來源于NGDC發布的研究海域部分數據，ETOPO1模型數據來自于Japan Oceanographic Data Center (JODC)、NGDC和The Mediterranean Science Commission(CIESM)等組織，S&S V18.1模型船測數據包括NGDC、SRTM Topography、SIO Multibeam、NGA Digital Nautical Soundings、JAMSTEC Multibeam等；輸入數據的豐富程度和數據質量優劣對最終海深模型質量影響明顯。二是海深模型構建方法差異，BAT_VGG模型使用控制點地形和重力數據之比獲取比例因子方法構建，而BAT_DG_Gauss模型和BAT_VGG_Moritz模型采用最小二乘配置方法建立，本文最小二乘配置方法實質上類似于回歸分析擬合導納系數，同時兼顧趨勢項小的變化。SAS方法獲取的比例因子是將控制點反演波段上地形和重力信息之比格網化，進而得到研究區域格網化的比例因子，采用該方法獲取的比例因子不同格網點結果不同；而本文采用最小二乘配置方法解算的研究海域地形和重力數據比例因子是基于對全域控制點處地形和重力信息考察的結果，反映了整個區域海底地形和海面重力的趨勢關系。從這一角度考慮，整個區域海底地形和海面重力的趨勢關系與導納函數反演海底地形方法類似。

分別沿研究區域南北和東西方向選擇各選擇一剖面位置，簡要比較各海深模型表現狀況，選擇的剖面位置如圖11(圖11背景為S&S V18.1海深模型)中1號位置(#1)和2號位置(#2)所示。采用雙線性插值方法作各海深模型在#1和#2的海深剖面圖，海深剖面結果如圖12所示。

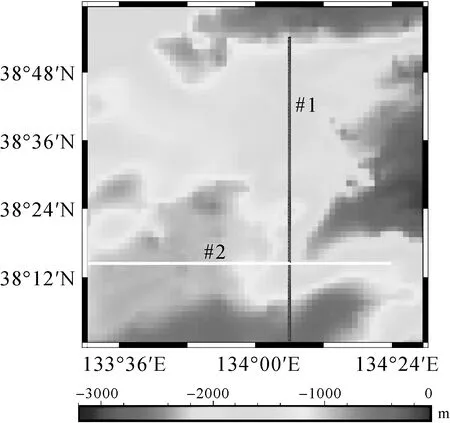
圖11 剖面位置Fig.11 Profile location

圖12 剖面深度圖Fig.12 Profile depth

海深剖面結果顯示，#1由南到北海底依次出現了海山、山谷、平原等地貌形態，#2剖面地形呈現是東西兩端為山地，兩端之間為山谷地形。#1和#2海深剖面結果顯示，BAT_DG_Moritz模型和BAT_VGG_Moritz模型地形走勢幾乎重合，二者相差很小；GEBCO模型相比其余模型地形走勢更加“平滑”，反映海底地形細部特征能力較弱，比如在#1緯度為38.4°左右的海山位置和#2經度為134.2°附近范圍的山谷位置，GEBCO模型反映地形能力有限；BAT_VGG模型在地形起伏區域，相比其他海深模型存在低估海山高度和高估山谷深度現象；ETOPO1模型在#1緯度為38.4°左右位置出現了與其余模型完全相反的地形呈現；BAT_DG_Moritz模型和BAT_VGG_Moritz模型在#1和#2均能較好反映對應位置的地形走勢，從而從側面說明了本文反演效果良好。

進一步描述和分析BAT_DG_Moritz模型和BAT_VGG_Moritz模型頻譜特征，依據文獻[41—43]可知，兩格網輸入數據的頻率域相干性(Coherency)是以波長為自變量的線性相關系數的平方，表征輸入數據間的線性相關程度。兩格網信號相干性計算公式為

Coh=

(18)

式中，Coh表示相干性；M(fx,fy)和N(fx,fy)代表格網信號m(x,y)和n(x,y)的傅里葉變換；“*”號表示復共軛；〈〉表示方位角取平均(Cartesian坐標系轉為極坐標系)。依據文獻[44—45]計算功率譜密度(power spectrum density，PSD)方法獲得不同波長對應的功率譜密度

PSD=10·lgP

(19)

式中，PSD單位是dB；P代表不同波長的能量。因S&S V18.1模型、ETOPO1模型、GEBCO模型和BAT_VGG模型構建過程中利用的數據源和數據量不同，從而主要對比BAT_DG_Moritz模型和BAT_VGG_Moritz模型頻譜特征信息，PSD和相干性結果如圖13所示。

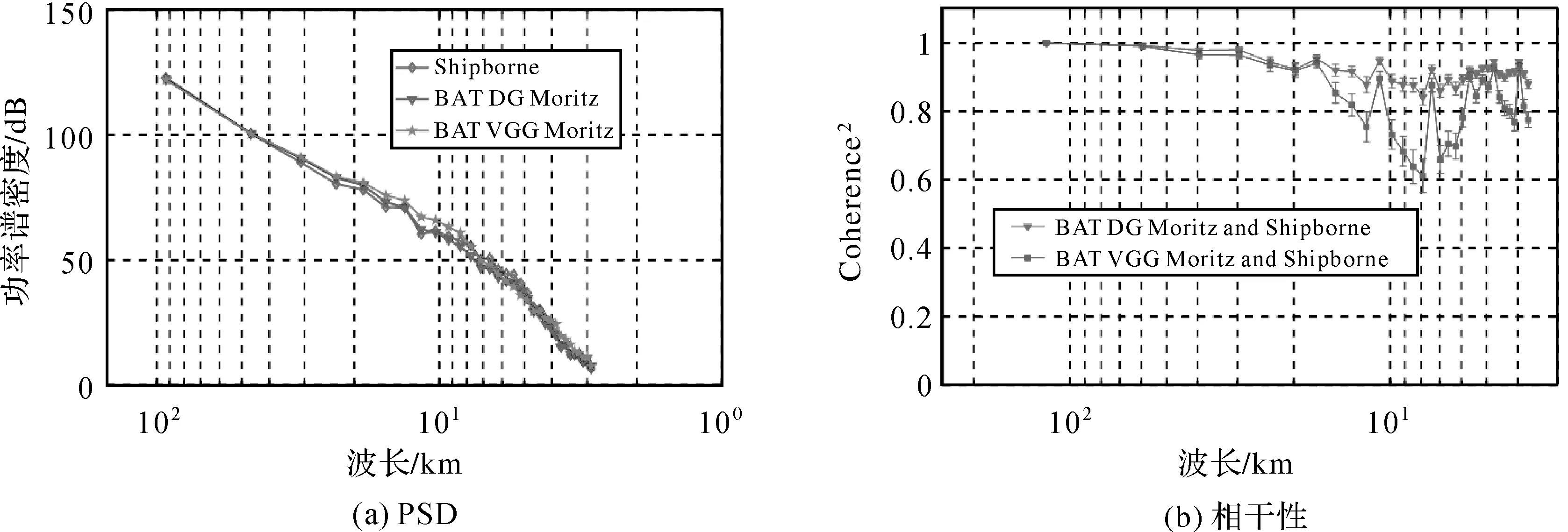
圖13 PSD和相干性分析Fig.13 PSD and coherency analysis

圖13中Shipborne為使用本文控制點數據，借鑒文獻[45]格網化方法(Gridding with spline in tension)獲取的格網化海深。利用式(19)計算的BAT_DG_Moritz模型、BAT_VGG_Moritz模型和Shipborne模型的功率譜密度折線如圖13(a)中藍色、綠色和紅色所示。PSD曲線顯示，BAT_DG_Moritz模型和BAT_VGG_Moritz模型可改善了Shipborne模型6 km波段以上信息，其中BAT_VGG_Moritz模型在高頻部分改善更加明顯。筆者在研究海區開展試算時，確定的帶通濾波器波長初值為15 km，而PSD曲線顯示最終反演海深模型卻改善了Shipborne模型6 km以上波段信息。究其原因，筆者認為是由于試算過程中選擇的濾波器本身機制所致。由于筆者使用帶通濾波器濾波時，小于15 km波長的信息并非完全濾掉，而是存在部分保留信息，進而呈現出最終反演海深模型改善的波段范圍大于初始選擇頻段現象。依據式(18)分別計算格網模型間的相干性，結果如圖13(b)所示，其中紅色折線表示BAT_DG_Moritz模型和Shipborne模型相干性結果，藍色折線代表BAT_VGG_Moritz模型和Shipborne模型相干性結果。從圖13(b)模型相干性結果可以看出，二者表現了較強的相干性(相干性結果均在0.5以上)，其中BAT_DG_Moritz模型和Shipborne模型相干性平均值分別為0.917 0。另外，BAT_DG_Moritz模型和BAT_VGG_Moritz模型相干性平均值達到了0.930 7。圖13(b)相干性折線均呈現先減小后增大趨勢，其中相干性減小波段是BAT_DG_Moritz模型和BAT_VGG_Moritz模型相對于Shipborne模型波段信息改善部分，其中重力異常垂直梯度反演海深結果與Shipborne模型相干性減小明顯，再次驗證了功率譜密度分析中關于BAT_VGG_Moritz模型在改善船測海深模型效能方面效果明顯結論。由于本文試驗在有限波段進行，因而對Shipborne模型短波和長波部分信息改善有限。

3 結 論

本文針對目前導納函數方法、SAS方法和回歸分析方法反演海底地形主要考慮海底地形和衛星測高重力數據線性趨勢項而忽略非線性項影響現狀，提出了采用最小二乘配置技術兼顧海底地形和重力數據線性項和與非線性項(與線性趨勢項不符的小的變化)構建海底地形模型新的方法途徑。然后，利用日本海某海域重力異常數據、重力異常垂直梯度數據和稀疏船測數據開展了方法試算驗證工作，同時將本文反演結果與國際廣泛使用的S&S V18.1和ETOPO1等海深模型進行了比對分析，可得到如下有益結論。

(1)相較于僅僅考慮海底地形和重力數據線性趨勢項而建立的海深模型BAT_DG_LS和BAT_VGG_LS，本文采用最小二乘配置方法，利用相同重力數據獲得的反演海深模型檢核精度最低分別提高了大約2.5倍和3.5倍，以及相對精度最高分別提升了9.76%和13.07%，極大提升了海底地形建模質量。

(2)本文最小二乘配置反演模型與S&S V18.1、ETOPO1、GEBCO和BAT_VGG模型在研究海域相關系數均達到了0.95以上。海深模型檢核差值和剖面海深分析結果表明：本文利用最小二乘配置方法構建的海深模型相對精度在3.8%范圍內，各精度指標與S&S V18.1模型相當，遠遠優于ETOPO1和BAT_VGG等海深模型；GEBCO模型相比其余海深模型反映地形更加“平滑”，反映海底地形細部特征能力較弱，BAT_VGG模型在地形起伏區域，相比其他海深模型存在低估海山高度和高估山谷深度現象。

(3)海深模型相干性和功率譜密度特征分析表明：本文反演模型能有效改善研究海域船測海深相關波段信息(本文反演波段范圍為15～160 km)，其中衛星測高重力異常垂直梯度相比重力異常為輸入源建立的海深模型改善船測海深相關波段信息更為明顯。

綜上所述，本文采用最小二乘配置方法，兼顧海底地形線性趨勢項和非線性項構建的海底地形模型表現良好，反演方法可行且有效。