溝壑地貌對上覆巖層破斷角的影響研究

武 濤，張光磊，王仲倫

(1.中煤華晉集團有限責任公司王家嶺煤礦，山西 運城 043300；2.中煤能源研究院有限責任公司，陜西 西安 710054；3.太原理工大學原位改性采礦教育部重點實驗室，山西 太原 030024)

西部地區煤炭資源儲量豐富，國家能源發展重心向西部轉移。西部地區地形地貌復雜，且覆蓋有大量黃土層，地表起伏較大，丘陵、溝谷發育，形成典型的黃土溝壑地貌[1]。研究在該種特殊地貌下巖層破斷規律，對煤炭資源綠色高效開采具有重要意義。

針對溝壑地貌下礦壓規律及巖層破斷的研究，前人做了許多工作。許家林等[2]通過現場實測、理論分析及相似模擬等方法研究了溝谷地形對淺埋煤層的動載礦壓顯現的影響，揭示了上坡段易發生動載礦壓的機理；張志強等[3-4]分別研究了溝深及溝谷坡角對工作面礦壓顯現的影響，所得規律與現場實測相吻合；李建偉等[5]利用數值模擬得到了開采深度增加，地表溝谷影響作用減弱的規律；張碧川等[6]以榆神府黃土溝壑區典型礦井為研究對象，確定了影響溝壑區開采沉陷的主要因素；羅竹等[7]通過數值模擬結合現場實測的方法對溝谷地貌下的礦壓進行了模擬研究，得到上坡段的巷道是重點支護區域；王鵬舉[8]針對溝谷地貌下開采礦壓顯現異常的現象，運用數值模擬及相似模擬確定了合理的支護方案；常江元[9]采用相似模擬及數值模擬相結合的方式對溝谷區域開采導水裂隙帶的發育進行了研究；趙杰等[10-12]對溝谷區域淺埋煤層開采導致的地表損害及采動應力場開展了研究，分析了礦壓顯現特征，提出了上坡階段動壓防治措施；戎虎仁等[13]研究了坡角對導水裂隙發育的影響；賀雁鵬等[14]運用鉆孔測井分析儀對頂板破斷角進行了實測；梁金朝等[15]導出了巖梁斷口的軌道曲線解析式。

本文以王家嶺煤礦12309工作面為研究背景，基于彈性力學及巖石力學建立了巖層破斷角力學模型，通過提取相似模擬試驗關鍵層承載載荷，得到溝底、坡頂及上坡開采過程中的應力變化規律，并對巖層破斷角的合理性進行了驗證，對指導溝壑地貌下煤炭資源的開采具有一定意義。

1 工程地質概況

以王家嶺煤礦12309綜放工作面為研究對象。王家嶺煤礦位于河東煤田鄉寧礦區西南部，且西部地貌特征明顯。由于王家嶺煤礦位于呂梁山脈南麓，地形較為復雜，屬侵蝕強烈的高山區、中山區，地表溝壑縱橫，形成大量V形山谷，坡度多處于25°～40°之間，地表被大量黃土層覆蓋。井田總體為單斜構造，斷層較發育，構造應力復雜，為典型的黃土溝壑地貌。

12309工作面推進長度為1 320 m，傾向寬度為260 m，煤層平均埋深為390 m，采用后退式完全垮落放頂煤采煤法，該工作面位置示意圖如圖1所示。工作面回采煤層為2#煤層，煤層賦存穩定，產狀平緩，結構較簡單，為半暗-半亮型煤，一般含1～2層炭質泥巖夾矸，煤層頂底板特征如圖2所示。

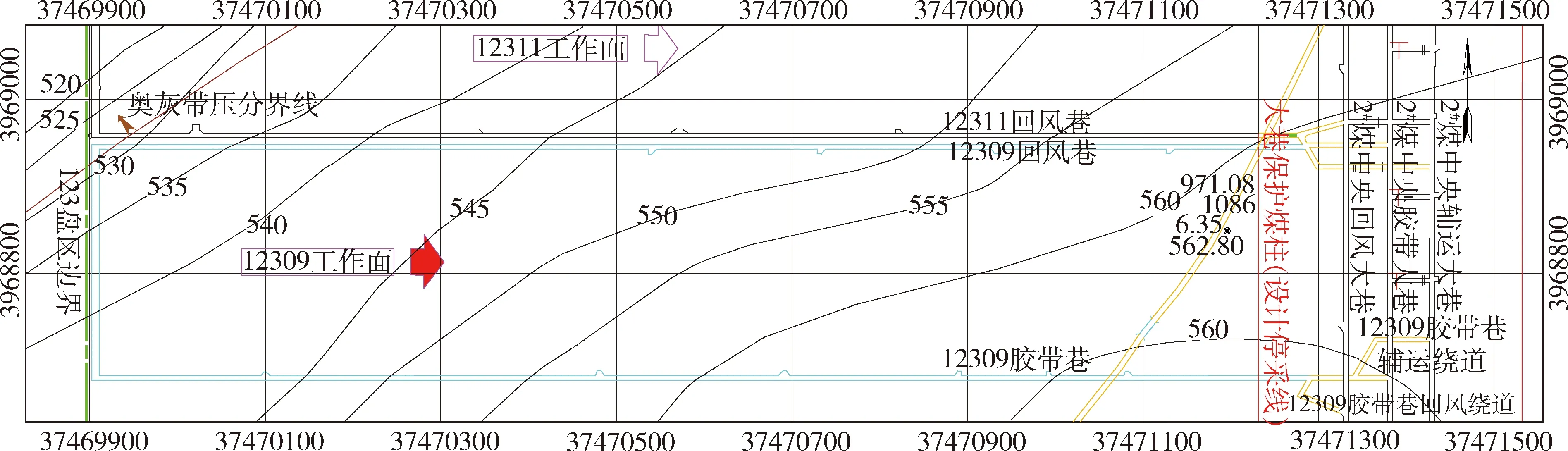
圖1 12309工作面位置圖

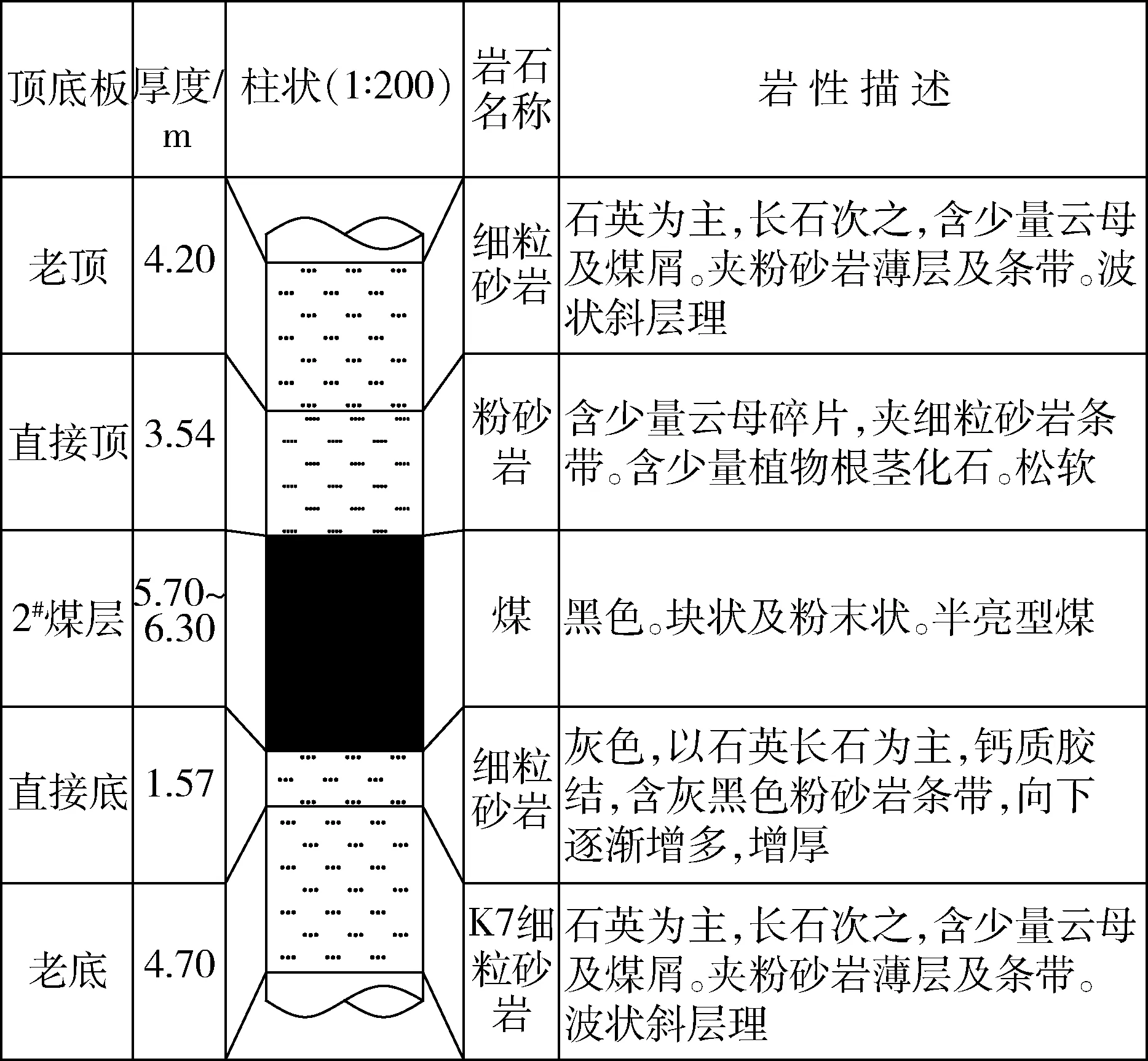
圖2 煤層頂底板巖性

2 破斷角理論分析

2.1 破斷巖梁應力分量求解

基于彈性力學及巖石力學，將破斷巖梁看做彈性均質體，忽略巖梁內部的原生裂隙。建立如圖3所示的巖梁破斷力學模型，并進行受力分析。

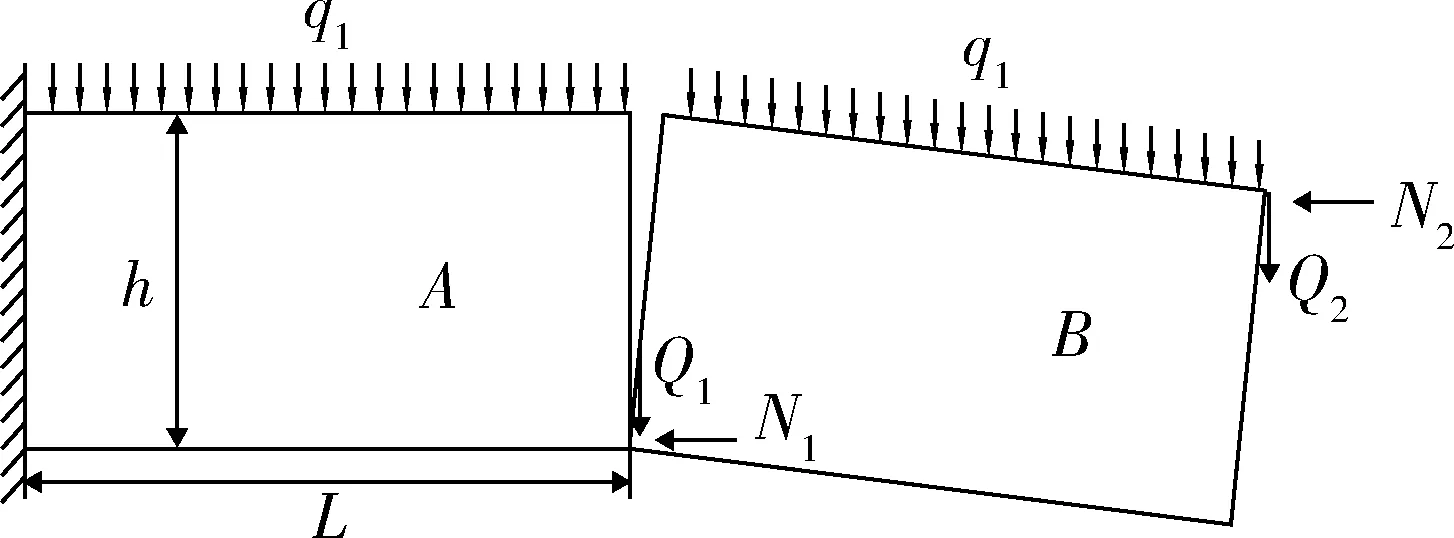
圖3 巖梁破斷力學模型

巖梁A表示未破斷巖梁，巖梁B表示已破斷巖梁。巖梁A左端固支，右端為自由端，受到已破斷巖梁B施加的水平擠壓力N1和垂直剪力Q1；破斷巖梁B右端受到上一破斷巖梁施于的水平擠壓力N2和垂直剪力Q2。為方便分析，做如下假設：巖梁A與破斷巖梁上方均受大小為q1的均布載荷，且兩塊體長度厚度均為L、h。由于破斷塊體回轉角較小，可忽略不計，故單獨對巖梁B進行受力分析，可得巖梁B自由端所受的水平擠壓力N1和垂直剪力Q1關系，見式(1)。

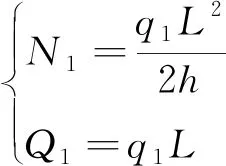
(1)

式中：N1為破斷巖梁B自由端所受的水平擠壓力，N；q1為破斷巖塊上方均受大小的均布載荷，N/m；L為破斷塊體長度，m；h為破斷塊體厚度，m；Q1為破斷巖梁B自由端所受的垂直剪力，N。

根據材料力學，將巖梁A視為在均布載荷q1及垂直剪力Q1作用下發生純彎曲，可得巖梁A的撓度Δ為式(2)。

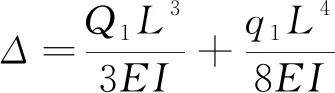
(2)

式中：Δ為巖梁A的撓度，m；E為巖體彈性模量，N/m2；I為巖梁A慣性矩，m4。

運用彈性力學，以未破斷巖梁固支端中點處為圓點建立直角坐標系，向右為x軸正方向，向下為y軸正方向。如圖4所示，通過試取應力函數，確定邊界條件，最終得到未破斷巖梁內部的應力分量為式(3)[16]。

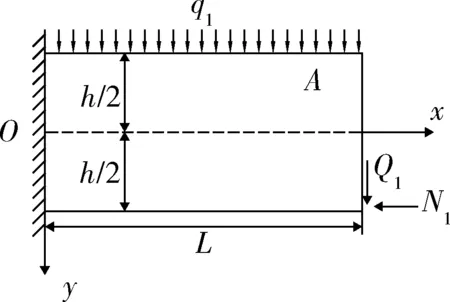
圖4 未破斷巖梁應力分析

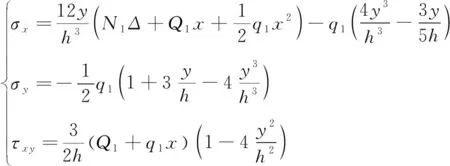
(3)

式中：σx為未破斷巖梁內部x軸方向應力分量，MPa；σy為未破斷巖梁內部y軸方向應力分量，MPa；τxy為未破斷巖梁內部剪切應力，MPa。

2.2 巖梁破斷角分析

在巖梁內部任意取一單元體，其受力狀態如圖5所示。

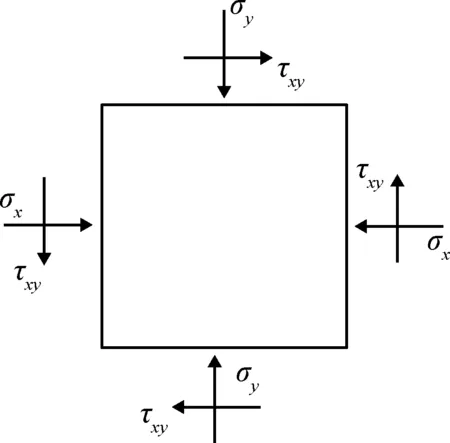
圖5 單元體應力狀態

根據材料力學可以得到單元體最大主應力σ1與正應力σx、切應力τxy之間的關系為式(4)。

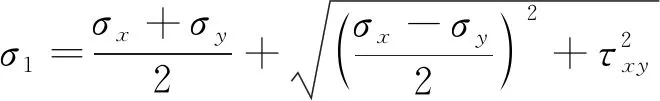
(4)

式中：σ1為單元體最大主應力，MPa；σx為單元體正應力x軸方向分量，MPa；σy為單元體正應力y軸方向分量，MPa。

最大主應力σ1與正應力σx的夾角α1的關系式見式(5)。

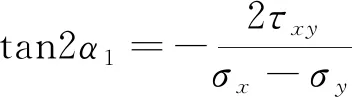
(5)

式中，α1為最大主應力σ1與正應力σx的夾角，(°)。

由式(5)可知夾角α1計算公式見式(6)。

(6)

將上述所求巖梁內部應力分量式(3)代入式(6)，由于巖梁大致位于坐標原點O位置處破斷，故令x=0，y=0，可得O點處最大主應力σ1與正應力σx的夾角α1的關系式見式(7)。

(7)

根據庫倫-摩爾準則可知，巖石破斷面與最大主應力面所成夾角為45 °+φ/2，則與最大主應力所成夾角α2的關系式見式(8)。

(8)

式中：α2為最大主應力所成夾角，(°)；φ為巖石內摩擦角，(°)。

由圖6可知，根據幾何關系可知巖梁破斷面與水平面的夾角α=α1+α2，代入式(7)和式(8)整理可得式(9)。

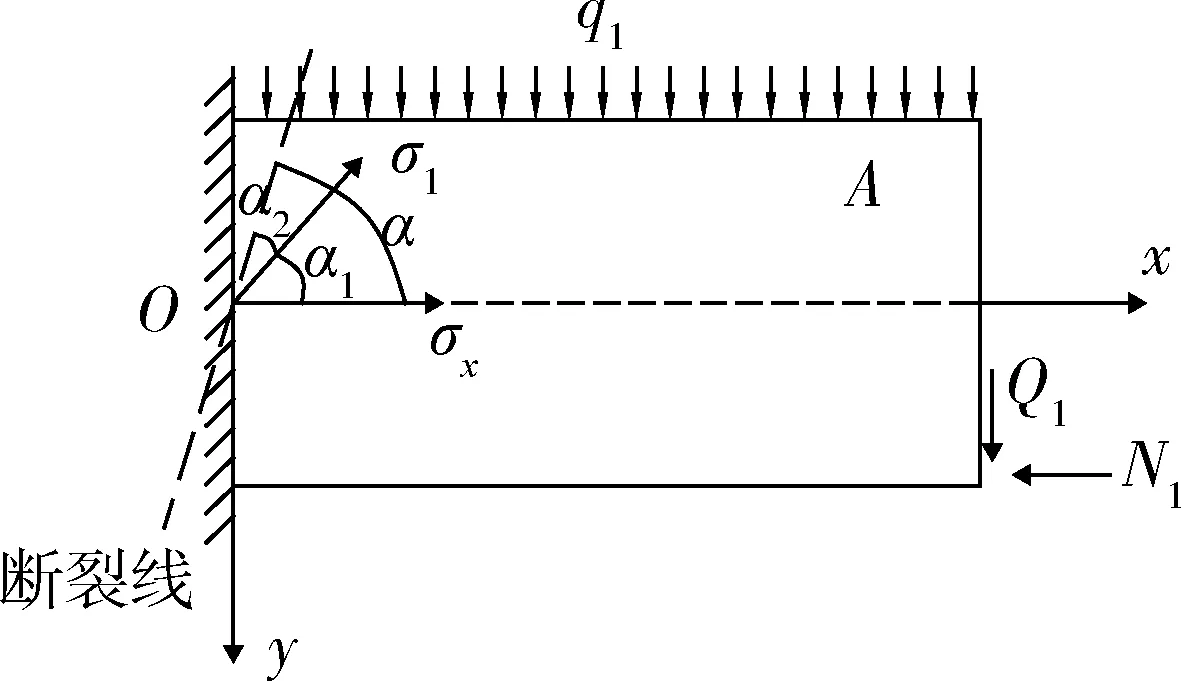
圖6 巖梁破斷面與水平面夾角

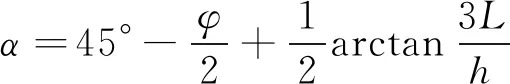
(9)

式中，α為巖梁破斷面與水平面的夾角，(°)。

根據材料力學估算出的巖層厚度h與破斷時懸露長度L之間的關系見式(10)。

(10)

式中：RT為巖梁抗拉強度，MPa；q為巖梁承載載荷，MPa。

將式(10)代入式(9)，整理可得式(11)。

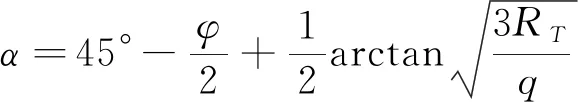
(11)

2.3 巖梁破斷角影響因素分析

通過彈性力學及材料力學相關理論分析，結合式(11)可知，巖梁破斷角α與巖梁承載載荷q、巖梁抗拉強度RT及巖層內摩擦角φ等因素有關。

假設巖層內摩擦角φ取為30°，巖梁承載載荷層q為2 MPa，繪出巖梁破斷角α與巖梁抗拉強度RT之間的關系曲線，如圖7所示。由圖7可知，巖層破斷角α隨抗拉強度RT的增加而單調遞增，抗拉強度較小時，破斷角增加速率較大；而隨著抗拉強度的增加，破斷角的增加速率逐漸變小，并逐漸趨于水平，總體增長趨勢與對數函數相似，由于關鍵層抗拉強度普遍大于2 MPa，可知關鍵層破斷角普遍大于60°。

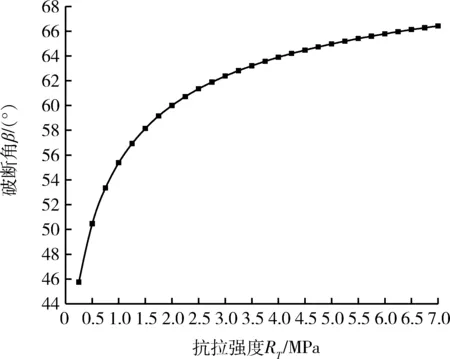
圖7 巖層破斷角與抗拉強度的關系

為研究巖梁承載載荷q與巖梁破斷角α之間的關系，取巖層內摩擦角φ取為30°，抗拉強度為5 MPa。繪出巖梁破斷角α與巖梁承載載荷q之間的關系曲線，如圖8所示。由圖8可知，巖層所承載的載荷越大，巖層破斷角越小，曲線斜率逐漸減小，載荷的增加對破斷角的影響逐漸減弱。結合上述分析可知，巖層破斷角范圍在60°～70°之間。

圖8 巖層破斷角與承載載荷的關系

3 物理模擬實驗研究

3.1 相似模型試驗

為研究溝壑地貌對關鍵層破斷角的影響，根據式(11)可知，如果能夠得到巖梁承載載荷q、巖梁抗拉強度RT及巖層內摩擦角φ，即可求出巖梁破斷角α的大小。其中，巖梁抗拉強度RT及巖層內摩擦角φ可以通過巖石力學參數的測定得到具體值；而巖梁承載載荷q由于溝壑地貌的影響，直接進行測量或理論分析較為困難，且存在較大誤差，故采用相似模擬的方法，重現地表溝壑地貌，并監測該地貌影響下關鍵層承載載荷的大小，將所測參數代入式(11)即可求得巖梁破斷角α。

根據王家嶺煤礦12309工作面地質狀況及巖層力學參數，采用黃土模擬溝壑地貌，進行試驗研究，模型尺寸示意如圖9所示。

圖9 物理模型尺寸

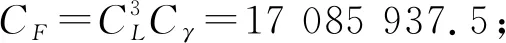
2) 相似材料。相似材料包括兩方面：骨料和膠結物。骨料主要用到砂子、云母粉、滑石、粉薪土等，膠結物有石膏、石蠟、碳酸鈣、水泥等。經過數次不同配比的試塊強度試驗后，最終確定合適的材料配比。本文以停采線西側1086號鉆孔為準，建立相似模擬模型進行研究。巖層力學性質見表1。

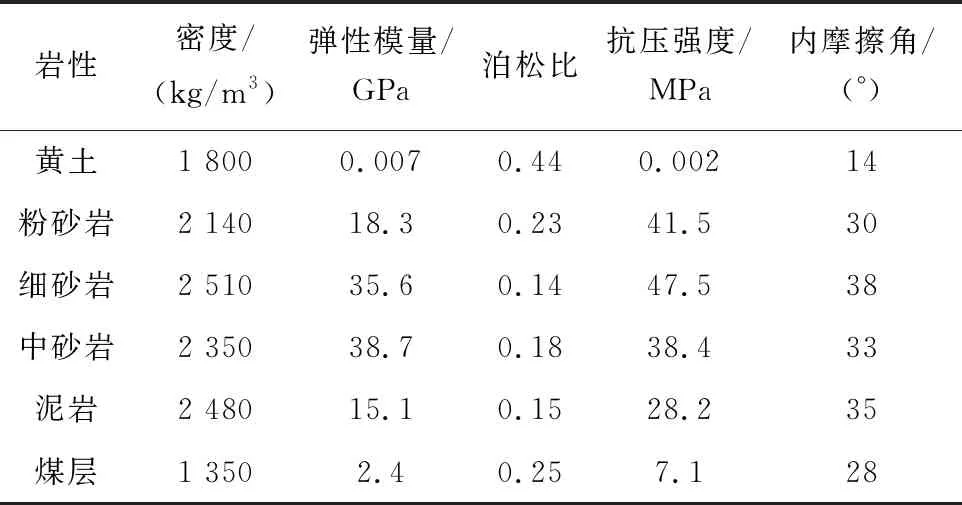
表1 巖層力學性質

3)主關鍵層層位確定。根據錢鳴高院士構建的采場覆巖關鍵層理論可知[17]，結合覆巖主關鍵層的厚度特征。強度特征以及支撐強度特征確定距煤層頂板175.7 m厚度為39.5 m的細粒砂巖層為主關鍵層，主關鍵層位置見圖9。

3.2 巖層破斷角分析

隨著工作面向前推進，頂板覆巖發生移動與破壞，形成垮落帶與裂隙帶，垮落帶隨工作面的推進范圍較為穩定，而裂隙帶則不斷向上發育。 如圖10(a)所示，覆巖中形成了大量采動裂隙，一類為巖層與巖層之間的離層裂隙，一類為隨巖層破斷而形成的豎向裂隙。當工作面推進至290 m時，裂隙不斷向上方發育，隨著厚度為39.5 m的主關鍵層下方巖層壓實，離層裂隙與豎向裂隙逐漸閉合、并在主關鍵層下方出現較大的離層空間，主關鍵層發生彎曲下沉，同時伴隨著裂隙的擴展與延伸，如圖10(b)所示。當模型中工作面推進完畢，待巖層破壞變形穩定后，離層空間逐漸減小，采空區中部裂隙閉合，兩側裂隙較為發育，如圖10(c)所示。可見主關鍵層在谷底側上坡開采階段彎曲下沉量較大，且裂隙更為發育；而在坡頂彎曲下沉量較小，且裂隙較少。由此可知，當工作面推進方向與溝谷走向垂直或斜交時，在上坡階段易出現應力集中，巖層承載載荷較大，彎曲下沉量大且裂隙發育。觀察關鍵層破斷角，左側破斷角約為71°，右側破斷角約為62°，可見谷底一側巖層破斷角較大。 通過觀察模型上方黃土層，如圖10(d)所示，可以清晰看到上坡階段黃土層產生大量裂縫，并擴展至地表。可見上坡階段應力集中明顯。

圖10 覆巖垮落形態圖

通過在模型中埋置土應力盒，監測主關鍵層所承載的載荷，如圖11所示。

由圖11可知，從谷底向坡頂開采的過程中，關鍵層承載載荷逐漸減小，明顯可見坡底處應力較大，最大為3.32 MPa；而坡頂應力較小，最小為1.14 MPa。將主關鍵層破斷處的應力值提取代入式(11)，并取巖層內摩擦角φ為30°，抗拉強度為4.7 MPa，得出谷底處巖層破斷角為62.1°，坡頂處巖層破斷角為67.1°，理論計算與物理實驗模擬結論相似。

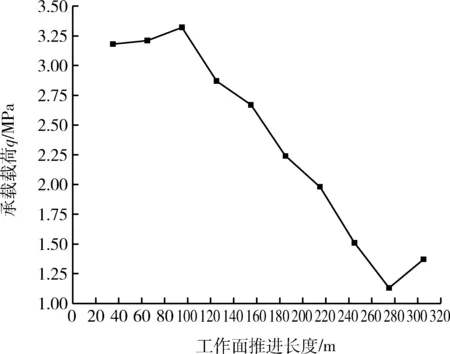
圖11 巖層載荷

4 結 論

1) 基于彈性力學、材料力學理論建立了巖梁破斷力學模型，推導出用于計算巖梁破斷角的理論公式，得出巖梁破斷角α與巖梁承載載荷q、巖梁抗拉強度RT及巖層內摩擦角φ等因素有關。

2) 分析巖梁破斷角α與巖梁抗拉強度RT之間的關系可知，巖層破斷角α隨抗拉強度RT的增加而單調遞增，當抗拉強度較小時，破斷角減小速率較大，后逐漸減小，曲線趨于平緩，總體變化趨勢與對數函數相似，說明抗拉強度對破斷角的影響隨其值的增大不斷減小。

3) 分析巖梁破斷角α與巖梁承載載荷q之間的關系可知，巖層所承載的載荷越大，巖層破斷角越小，曲線斜率逐漸減小，載荷的增加對破斷角的影響逐漸減弱。綜合分析關系曲線可知，巖層破斷角范圍在60°～70°之間。

4) 運用相似模擬試驗提取關鍵層承載載荷，發現谷底處應力大于坡頂，上坡開采階段裂隙更為發育，且關鍵層下沉量較大，說明谷底處有應力集中。將應力值代入破斷角計算公式，得出谷底處破斷角小于坡頂處，驗證了破斷角計算公式的合理性。