基于改進型ARIMA-GRNN模型的高邊坡變形預測

段青達, 陳天偉, 田立佳, 鄭旭東, 陳 明

(1.桂林理工大學 a.廣西空間信息與測繪重點實驗室; b.測繪地理信息學院, 廣西 桂林 541006;2.廣西交投科技有限公司, 南寧 530012)

0 引 言

由于受降雨、 地下水、 風化等因素的影響, 原本穩定的高邊坡極易出現滑坡現象[1]。為了保證工程施工和運行的安全, 對邊坡進行長期監測并預測其變形趨勢至關重要[2]。

目前常用的預測模型有: 時間序列分析預測法、 神經網絡、 灰色模型、 遺傳算法等[3], 各種預測模型都取得了一定的成果, 但也存在一定的局限性[4]： 灰色模型對樣本數據具有很強的依賴性, 短期預測較好； 遺傳算法訓練時間長, 對參數的選擇沒有準確的標準； 而時間序列分析法能較好地突出高邊坡位移變形隨時間的變化關系； 神經網絡具有很強的魯棒性和容錯性, 可以充分逼近任意復雜的非線性關系[5]。

本文提出了將差分整合移動平均自回歸模型[6](ARIMA)與廣義回歸神經網絡(GRNN)聯合的方法運用到高邊坡變形預測中, 利用ARIMA模型本質上只能捕捉線性關系而不能捕捉非線性關系[7]、 GRNN神經網絡對非線性數據具有極強的映射能力[8], 將二者耦合, 組建ARIMA-GRNN模型。原始的觀測數據中可能存在大量的噪聲, 由于噪聲的存在直接影響了觀測數據的波動性[9], 致使ARIMA模型前期無法準確獲取高邊坡位移實際的變形趨勢, 從而降低了GRNN神經網絡后期的預測效果。現階段研究發現, 常用的消噪方法主要有小波分析[10]與集合經驗模態分解[11](EEMD)。 小波分析能有效提取低頻有用信息, 但容易忽略中高頻有用信息[12], 同時選擇不同的小波基和分解層數, 對消噪效果的影響很大[13], 從而加大了小波分析消噪的難度。而集合經驗模態分解通過觀測數據自身的時間尺度對信號進行分解, 不需預先設定任何的基函數[14], 在處理非線性、 非平穩的信號序列方面具有明顯的優勢。 目前， EEMD消噪常用的方法主要通過篩選出高頻的本征模態分量(IMF), 將其作為噪聲直接剔除[15], 這樣做雖然能達到一定的消噪效果, 但也丟失了高頻IMF分量的細節信息, 而且其他頻率的IMF分量中的噪聲也不能有效地剔除。為了挑選出高頻噪聲信號中隱含的低頻信號, 盡可能獲取更多有用信號, 本文采用EEMD與奇異值分解(SVD)結合的方法實現對觀測數據的消噪, 通過對觀測數據進行EEMD分解(剔除觀測數據中的低頻閃爍噪聲), 得到一系列本征模態分量, 實現信號的初次濾波； 再對EEMD分解后的各本征模態分量構建Hankel矩陣； 利用SVD分解對矩陣進行處理, 得到由大到小的奇異值, 其中噪聲具有較小的奇異值, 有用信號主要會集于較大的奇異值, 將代表噪聲信號較小的奇異值歸零后進行SVD重構[16]； 利用SVD分解對周期性及平穩性信號降噪具有較好的不變性及穩定性[17]特點實現信號的二次濾波(剔除各IMF分量中的高頻白噪聲), 即可完成信號的消噪。

本文提出的基于EEMD-SVD的ARIMA-GRNN預測模型, 不僅能較好地濾除各IMF分量中的高頻白噪聲, 還能保留各自的細節信息, 在一定程度上降低了ARIMA-GRNN模型建模的難度, 將其應用到高邊坡累積水平位移變形監測的預測當中, 以改良高邊坡變形數據的預測結果。

1 算法介紹

1.1 集合經驗模態分解(EEMD)

EEMD是經驗模態分解(EMD)的一種改進方法, 它在很大程度上解決了EMD模態混淆的問題[18]。通過對原始信號的平穩化處理得到頻率由高到低的一系列IMF分量和余量B[19]。EEMD分解步驟如下: 向高邊坡觀測數據的時間序列{x(t)}中多次加入強度相同但序列不等的正態分布白噪聲信號, 將加入的白噪聲信號看作一個整體, 進行EMD分解[20], 對多次得到的各IMF分量進行疊加求和, 再對每次得到的IMF分量作集成平均處理, 即可得到理想的IMF值。

1.2 奇異值分解(SVD)

SVD分解是一種以相空間重構矩陣為基礎的非線性濾波方法[21], 能較好地濾除周期信號與平穩性信號中的噪聲成分, 被廣泛應用在信號處理中。對于任意一個實數矩陣Am×n可表示為

(1)

其中:U是m×m階正交矩陣;Λ是m×n階對角矩陣;V是n×n階正交矩陣;Λ對角線上的元素(λ1,λ2, …,λn)即為A的奇異值;U和V分別為左奇異向量和右奇異向量。利用ATA的正交單位向量(v1,v2, …,vn)組成右奇異向量V。

(ATA)vi=λivi;

(2)

(3)

同理,AAT的正交單位向量(u1,u2, …,un)組成左奇異向量U。ω為奇異值, 在矩陣Λ中, 按照從大到小排列, 而且下降速度極快, 取前面若干大的奇異值近似描述矩陣, 再利用奇異值的逆運算即可得到重構后的信號。

1.3 差分整合移動平均自回歸模型(ARIMA)

ARIMA模型常被寫為ARIMA(p,d,q), 其中p是自回歸項,d是差分次數,q是移動平均項數, 通過對ARMA模型d階差分將非平穩的時間序列轉化為平穩的時間序列[22]。定義一維非平穩高邊坡觀測數據的時間序列為{Gt}, ARIMA(p,d,q)模型可表示為

(4)

左小龍跨在摩托車上，目光迥然，神情堅定，包括泥巴在內的所有人都詫異的看著如同雕塑一般的左小龍，一時沒有了言語。

1.4 廣義回歸神經網絡(GRNN)

GRNN神經網絡由4部分構成: 輸入層、 模式層、 求和層和輸出層[23]。它對處理非線性問題具有極強的映射能力和學習速度, 算法原理為： 設x為隨機變量, 函數值為y, 真實觀測值為H, 聯合密度函數為g(x,y), 函數值y的預測值Z為

(5)

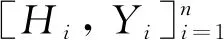
(6)

其中:σ為光滑因子,n為樣本數量。

1.5 建立基于EEMD-SVD的ARIMA-GRNN模型

針對高邊坡觀測數據多噪聲、 非線性的特點, 提出了一種基于EEMD-SVD的ARIMA-GRNN預測模型。首先利用EEMD分解濾除觀測數據中的低頻閃爍噪聲, 其次通過對各IMF分量進行SVD分解, 濾除各IMF分量的高頻白噪聲, 對消噪后的各IMF分量分別建立ARIMA模型, 作線性回歸預測, 將ARIMA預測后的結果疊加, 作為GRNN神經網絡的輸入層進行訓練, 即可得到最終的預測結果。算法流程如圖1所示。

圖1 基于EEMD-SVD的ARIMA-GRNN建模流程圖

2 實驗分析

2.1 數據處理

高邊坡變形數據的預處理分為兩個步驟: 1)設監測點的變形位移時間序列為Zm(m=1, 2, …,n), 對Zm作一階差分得Dm, 差分序列Dm的均值為CDm, 標準差為σ, 即當|Dm-CDm|/σ>3時, 則認為是奇異值(粗差), 取相鄰兩點Zm-1與Zm+1的均值代替Zm點; 2)由于高邊坡監測數據x、y(x為EW方向形變位移,y為SN方向形變位移)在一天內的數值變化不大, 故將監測數據按天進行平滑, 采集頻率為1次/h, 即每24 h取一次平均。

圖2 BD02、BD06監測點累計水平位移觀測值

BD02、 BD06累積水平位移在120 d內波動性較強, 無明顯的規律可循, 若直接用于建模, 很難達到理想的效果, 故對前105 d的數據進行消噪處理。在真實的高邊坡觀測數據中, 包含真實值與噪聲兩部分, 為了剔除觀測數據中的噪聲, 首先對觀測數據進行EEMD分解, 得到6個本征模態分量, 再利用SVD分解將各IMF分量噪聲分離, 即可得到純凈的IMF值。SVD分解噪聲分離原理: 隨機取一組IMF分量的觀測序列為Y={y(1),y(2), …,y(N)}, 構造Hankel矩陣

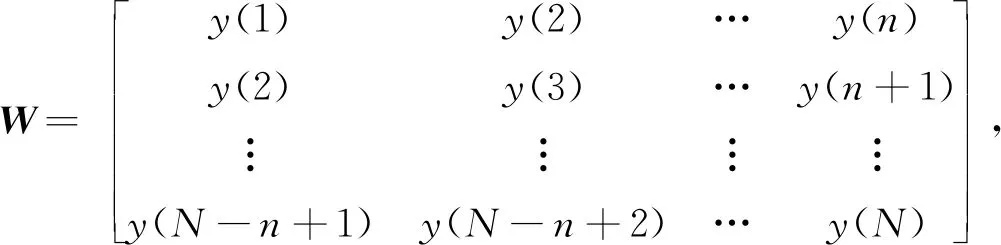
(7)

W=Z+T。

(8)

通過式(1)將W分解為

(9)

式中: 下標z表示真實序列的相關矩陣,t表示噪聲序列的相關矩陣。 通過SVD分解找出前面若干大的奇異值, 去除代表噪聲信號較小的奇異值, 即可完成對噪聲的分離。

對監測點BD02、 BD06觀測數據前105期進行EEMD和EEMD-SVD消噪處理。由圖3a、 圖4a可以看出,IMF1為第一高頻部分, 包含了觀測數據中的噪聲、 周期誤差等, 經過EEMD-SVD消噪處理后, 明顯降低了IMF1分量的波動性, 同時也保留了該分量的細節信息; 圖3b、 圖4b為第二高頻部分, 包含了觀測數據中的噪聲、 周期誤差的殘余量等, 通過EEMD-SVD消噪處理后, 使得消噪后的曲線整體上更加平滑, 在一定程度上降低了該分量的波動性; 圖3c、 圖4c為第三高頻部分, 包含了觀測數據中的噪聲、 周期誤差分量的殘余量等, 消噪處理后的曲線在拐點與極值點處變的更加平滑; 圖3d—f、 圖4d—f為低頻部分, 經過EEMD分解后趨勢已經十分明顯, 波動性也較小, 消噪前與消噪后并未發生太大變化。

圖3 BD02監測點各頻率分量與去噪后效果對比

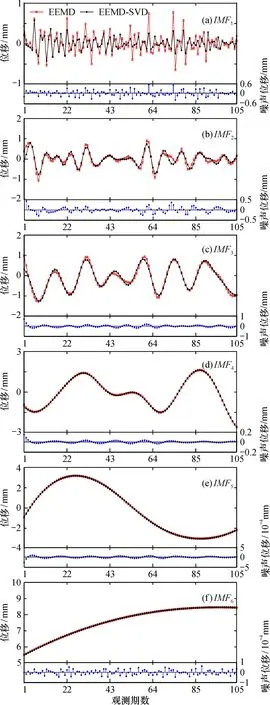
圖4 BD06監測點各頻率IMF與去噪后效果對比

2.2 預測模型

2.2.1 EEMD-SVD-ARIMA預測模型 通過對BD02、 BD06監測點觀測數據的EEMD-SVD處理, 得到6組消噪后的數據, 每組包括105期數據, 以此作為訓練樣本, 分別對各分量建立ARIMA(p,d,q)模型, 預測后15期數據, 對于得到的6組預測結果疊加求和, 即為ARIMA(p,d,q)模型的預測輸出。ARIMA模型建模參數如表1所示。

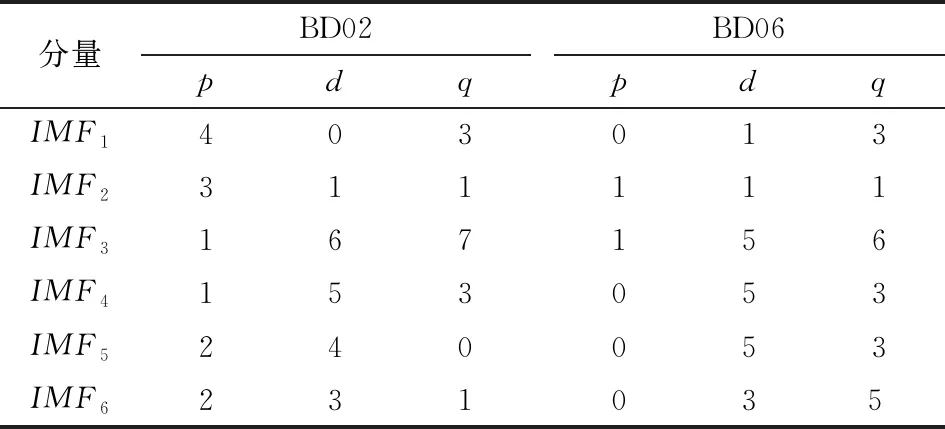
表1 各監測點建模參數

2.2.2 EEMD-SVD-GRNN模型與基于EEMD-SVD的ARIMA-GRNN模型 EEMD-SVD-GRNN模型構建的思路: 選取BD02、 BD06監測點觀測數據EEMD-SVD消噪后的6組數據疊加, 分別作為基于GRNN神經網絡的輸入層、 模式層、 求和層傳遞函數, 為了避免過擬合現象, 以后15期觀測數據作為輸出層。

EEMD-SVD的ARIMA-GRNN模型的實現步驟為: 選取BD02、 BD06觀測數據消噪后的6組數據分別構建ARIMA模型, 結合預測的15期數據, 共計120期數據, 對各分量疊加求和, 即ARIMA模型的預測值作為GRNN神經網絡的輸入層、 模式層、 求和層傳遞函數, 為了避免局部最小值問題, 以后15期觀測數據作為輸出層。

建立GRNN神經網絡預測模型時, 光滑因子的選取尤其重要, 本文通過交叉驗證和循環訓練的方法, 得出最佳的Spread值。當BD02、 BD06的光滑因子分別為1.4、 0.7時, GRNN神經網絡預測效果最佳; 當BD02、 BD06的光滑因子分別為0.7、 0.5時, EEMD-SVD-GRNN模型外推能力最強; 當BD02、 BD06的光滑因子分別為0.8、 0.4時, 基于EEMD-SVD的ARIMA-GRNN模型對樣本數據的逼近能力最強, 圖5為BD02、 BD06交叉驗證后的均方誤差。

圖5 各種模型下不同光滑因子的均方誤差

2.3 精度評定標準

為了驗證基于EEMD-SVD的ARIMA-GRNN模型的有效性, 本文選取均方誤差(MSE)、 平均絕對誤差(MAE)、 平均相對誤差(MRE)、 相關系數(R)作為精度評定的標準。

(10)

(11)

(12)

(13)

2.4 預測結果分析

本文利用基于EEMD-SVD的ARIMA-GRNN預測模型對高邊坡累積水平位移變形數據進行預測, 為檢驗該模型的合理性和可行性, 選取BD02、 BD06監測點前105期變形數據進行建模, 分別運用ARIMA模型、 EEMD-SVD-ARIMA模型, GRNN神經網絡模型、 EEMD-SVD-GRNN模型, ARIMA-GRNN模型和基于EEMD-SVD的ARIMA-GRNN預測模型對剩余的15期數據進行預測。

預測結果如圖6、圖7所示。ARIMA預測模型整體趨勢和觀測值的趨勢基本一致, 但存在一定的滯后性, 相當于將觀測值曲線向右平移1個單位, 而消噪后的ARIMA模型更能反映觀測值的實際走勢(圖6a); ARIMA模型整體殘差較大, 尤其在115、 116、 117期預測曲線明顯偏離。實際觀測值的曲線波動性較大, 而未消噪的GRNN神經網絡預測曲線表現的“過于平穩”, 經EEMD-SVD消噪后的預測曲線波動性更強, 整體殘差更小(圖6b)。基于EEMD-SVD的ARIMA-GRNN模型在短期內反應更加靈敏, 在108、 112、 116期拐點處相較與ARIMA-GRNN模型有了明顯改善(圖6c)。相較于消噪后的ARIMA模型、 GRNN神經網絡模型, 本文提出的基于EEMD-SVD的ARIMA-GRNN預測模型整體殘差最小, 更接近觀測值的實際趨勢: 112～113期, 本文模型和觀測值都為上升趨勢, 而另外兩種模型為下降趨勢; 108、 111、 116期拐點處和另外兩種模型相比更貼近觀測值(圖6d)。根據精度評定標準得到各模型的預測情況如表2所示。

表2 各模型預測精度對比

圖6 監測點BD02第106—120期各模型累計水平位移預測結果

圖7 監測點BD06第106—120期各模型累計水平位移預測結果

經過EEMD-SVD消噪處理后, 各預測模型的精度都有所提高。BD02監測點的結果表明, 本文模型相較于EEMD-SVD-GRNN模型MAE、MSE、MRE分別減少了32.28%、 71.03%、 31.91%,R增加了6.83%; 相較于EEMD-SVD-ARIMA模型MAE、MSE、MRE分別減少了34.95%、 50.14%、 34.69%,R增加了3.76%。本文模型在BD06監測點同樣適用, 消噪后模型的精度高于不消噪的模型, 與EEMD-SVD-GRNN模型相比, 本文模型MAE、MSE、MRE分別減少了53.15%、 79.22%、 43.54%,R增加了0.19%; 而與EEMD-SVD-ARIMA模型相比,MAE、MSE、MRE分別減少了53.70%、 75.04%、 57.18%,R增加了0.15%。

綜上所述, 本文提出的基于EEMD-SVD的ARIMA-GRNN預測模型應用在高邊坡變形預測中, 具有較高的適用性和外推能力。

3 結 論

本文提出了基于EEMD-SVD的ARIMA-GRNN預測模型, 通過對高邊坡變形數據的研究發現, 實際的高邊坡觀測數據中, 由于受多種因素的影響, 常存在噪聲, 噪聲的剔除應成為變形預測研究中必不可少的步驟。針對高邊坡觀測數據非線性、 復雜性問題, 通過對比分析, 該模型能較好地剔除觀測數據中的噪聲, 并且預測精度優異, 為高邊坡變形預測的研究提供了一種立竿見影的方法。