基于云遺傳算法優化BP神經網絡的軌道客流預測

唐秋生, 王 川

(重慶交通大學 交通運輸學院, 重慶 400041)

0 引 言

目前, 單一的神經網絡預測模型不能滿足客流預測的需求。需要優化神經網絡模型以提升預測算法的準確性[1]。 董升偉以北京市城市軌道交通4號線的歷史客流數據作為歷史數據庫, 將城市道路交通客流預測方法應用到城市軌道交通的客流預測中, 利用前饋(back propagation, BP)神經網絡的一些特點并結合聚類分析和相關性分析, 對城市軌道交通的客流預測進行分析, 仿真結果表明該方法提升了客流預測的精度[2]; 鄒巍等對于城市軌道交通客流變化具有的非線性和不確定性進行研究, 將遺傳算法和小波分析相結合, 建立了一種全局搜索最優的組合神經網絡預測模型, 解決了選擇神經網絡預測時容易造成過擬合的問題, 仿真結果表明， 該算法的預測結果比單一的神經網絡更加接近于真實值[3]; 毛靜針對支持向量機算法的單一核函數的一些缺點進行改進, 將支持向量機算法的核函數從一維改進成多維, 由于徑向基函數(radial basis function, RBF)神經網絡與支持向量機算法在單項預測法上的諸多優點, 將兩種算法進行組合形成組合預測模型, 并以清明假期的客流數據進行仿真分析, 得出組合預測模型優于單一預測模型的結論[4]; 李少偉等將卡爾曼濾波算法和Elman神經網絡進行組合, 先用混合神經網絡進行客流的初步預測, 然后使用卡爾曼濾波算法對初步預測的結果進行校準, 從而得到最后的預測結果, 對上海軌道交通客流數據進行仿真[5], 該算法比單一的混合神經網絡預測算法的預測精度提升了0.8%; 劉韻[6]將免疫粒子群算法(immune particle swarm optimization, IPSO)引入神經網絡, 同時引入生物免疫中的濃度選擇機制, 在保證粒子多樣性的同時, 確保粒子群快速收斂, 然后將優化處理后的權值帶入神經網絡模型結構中, 提高模型的運算速度與精度； 齊璐[7]利用狼群算法對小波神經網絡進行優化, 在預測前使用狼群算法計算小波神經網絡的最優權值和小波因子, 據此構建小波神經網絡模型, 隨后對歷史誤差值進行預測與結果相加, 結果表明, 該模型提高了小波神經網絡的預測精度；盧獻健等[8]將遺傳算法(GA)和粒子群算法(PSO)的尋優過程進行融合, 利用GA的全局性和PSO收斂速度快的特點, 通過迭代選取最優的粒子作為BP神經網絡的連接權值和閾值, 以減小網絡輸出誤差, 提高其收斂速度和加強網絡泛化能力； 劉林波等[9]利用影響霧霾的主要因素作為預報因子, 采用遺傳算法優化后的BP(GA-BP)神經網絡建立了PM2.5質量濃度預測模型, 并對其進行可靠性分析。

綜上, 現有研究主要集中在優化神經網絡結構與其他算法進行結合, 通過算法互補來提高神經網絡模型的預測精度。本文根據云模型及遺傳算法自身的特點, 提出一種基于云遺傳算法優化BP神經網絡的客流預測模型, 應用重慶軌道交通3號線客流數據及Matlab編程工具, 對3號線的交通流量進行預測, 并與傳統BP神經網絡與遺傳算法優化BP神經網絡的預測結果進行比較。

1 理論模型

1.1 云理論

1995年, 中國工程院院士李德毅提出了云模型的概念, 云模型是處理定性概念與定量描述的不確定轉換模型[10]。定義如下: 設T為論域u上的語言值, 映射CT(x):u→[0, 1], ?x∈u,x→CT(x), 則CT(x)在u上的分布稱為T的隸屬云, 簡稱“云”, 當CT(x)服從正態分布時, 簡稱正態云模型[11]。如圖1所示。

圖1 正態云分布

云的數字特征用期望Ex、 熵En、 超熵He3個數值來表示。期望Ex(expected value): 云滴在論域空間的分布期望, 就是最能代表定性概念的點, 也是這個概念量化的最典型樣本[11]。熵En(entropy): 定性概念的不確定性度量, 由概念的隨機性和模糊性共同決定[11]。超熵He(hyper entropy): 是熵的不確定性度量, 即熵的熵, 由熵的隨機性和模糊性共同決定[11]。

云發生器[12]是從定性概念到定量表示的過程, 也就是由云的數字特征產生云滴的具體實現, 包括正向及逆向正態云發生器以及X條件發生器和Y條件發生器。

1.2 云遺傳算法

遺傳算法(GA)是借鑒生物進化中“適者生存”自然規律的特征, 隨機產生可行性解, 并通過一定的機制進行選擇、 交叉和變異操作產生最優解或近似最優解的隨機優化算法。標準遺傳算法(SGA)在交叉和變異操作算子中采用確定性的固定概率進行, 算法存在未進化至最優解時已經收斂或者收斂的速度太慢, 使算法的實際應用性不強。

云遺傳算法結合遺傳算法思想, 沿用傳統遺傳算法的交叉、 變異操作概念, 由正態云模型的X條件云生成算法生成迭代過程中的交叉概率Pc和變異概率Pm。正態云模型具有隨機性和穩定傾向性的特點, 隨機性可以保持個體多樣性從而避免搜索陷入局部極值, 而穩定傾向性又可以很好地保護較優個體從而對全局最值進行自適應定位, 從而滿足快速尋優的能力, 并根據其隨機性能避免陷入局部最優。生成遺傳算法的交叉概率、 變異概率具體算法如下所示。

1)Pc的生成算法

Enn=normrnd(En,He)；

2)Pm的生成算法

Enn=normrnd(En,He)

其中,f′為交叉操作中較大的適應值；f為變異操作中父代染色體的適應度值；k1、k2、k3、k4為[0, 1]內的常數。在云遺傳算法中可取初始C1=C3=6Q(Q為初始種群的大小), 并且隨進化代數逐漸增大, 在此設置C1=C3=6Q(T+1)，其中T為進化代數[13]。為了算法運行初期擴大搜索空間, 運行后期提高搜索精度,He可以先大后小的設置[13], 如C2=C4=15-(T-Q/2)2。

2 基于云遺傳算法的BP神經網絡

2.1 基本思想

BP神經網絡有很多固有缺陷, 如結構難確定、 初始權值選擇的盲目性導致訓練速度慢、 容易陷入局部最優等。遺傳算法是基于自然選擇和遺傳學機理的迭代自適應概率搜索算法, 經云模型優化后的遺傳算法具有全局尋優、 快速收斂等優點, 利用云遺傳算法的這些特性, 可以解決神經網絡的上述缺點, 有益于交通量預測準確性的提高。

本文將云遺傳算法和BP神經網絡結合起來, 提出基于云遺傳算法的BP神經網絡模型, 基本思想是由云模型的X條件云發生器生成遺傳算法中的交叉概率和變異概率, 利用改進后的遺傳算法對BP神經網絡的初始權值和閾值進行優化。云遺傳算法優化得到的最優個體, 即BP神經網絡的最優初始權值、 閾值。利用得到的最優初始權值、 閾值和歷史數據來訓練BP神經網絡預測模型以求得最優解。算法流程如圖2所示。

圖2 算法流程圖

2.2 算法設計

算法的基本步驟如下:

(1)參數初始化。首先, 初始化遺傳算法參數, 包括初始種群大小Q、 最大進化代數G等； 其次, 云模型控制系數初始化,C1=C3=6Q(T+1),C2=C4=15-(T-Q/2)2； 最后, 確定神經網絡的結構, 包括輸入輸出及隱含層節點數、 學習率、 權值wi和閾值bi初始化等。

(2)編碼。本文采用實數編碼方式對神經網絡的初始權值和閾值進行編碼, 將wi和bi統一編碼到每個個體當中, 每個個體就代表一組神經網絡初始權值和閾值。

(3)產生初始種群。按照編碼方式, 隨機產生大小為Q的初始種群。

(4)計算適應度。本文選用平均絕對誤差作為適應度函數

其中：Ei為第i個體的均方誤差；n為訓練樣本總數；ti為第i個體的預測值；yi為第i個體的實際輸出值。

(5)選擇、 交叉、 變異。①選擇: 輪盤賭選擇個體。②交叉: 利用X條件云發生器生成交叉概率, 如果父代中較大的適應度值大于種群的平均適應度值, 那么根據云模型生成的交叉率進行交叉操作； 否則, 按照固定交叉率進行交叉。交叉方式為兩染色體對應基因段交叉。③變異: 利用X條件云發生器生成變異概率, 如果該染色體的適應度值大于種群的平均適應度值, 那么根據云模型生成的變異率進行變異操作； 否則, 按照固定變異率進行變異。變異方式是染色體某基因點變異。

(6)判斷是否滿足要求。判斷交叉變異后的個體是否達到要求(最大進化代數Q或適應度值在允許的誤差范圍內)。如果滿足要求, 則輸出最優個體, 再解碼得到BP神經網絡的最優初始權值和閾值; 否則, 重新回到步驟(4), 直到滿足條件為止。

3 算例分析

采用BP神經網絡預測模型(BP)、 遺傳算法優化BP神經網絡預測模型(GA-BP)、 云遺傳算法優化BP神經網絡預測模型(CGA-BP)3種預測方法對重慶市軌道交通3號線的客流進行預測。 先對數據進行歸一化處理, 將數據處理到[0, 1], 再將其中80%的數據用于訓練, 10%的數據用于驗證, 剩下10%的數據用于測試。實驗誤差評價采用平均絕對誤差MAE和均方誤差MSE。

其中：n為交通流數據個數；xk為交通流真實數據；xk′ 為交通流預測數據。

3.1 參數分析確定

3.1.1 BP神經網絡參數的確定 本文設計只有1個隱含層的BP神經網絡預測模型, 神經網絡的輸入為預測天前一天、 預測天和上一周與預測天同星期的日客流量3個輸入向量, 輸出向量為預測天的日客流量。例如, 預測天為第10周星期四, 則輸入變量為: 第10周星期三、 星期四、 第9周星期四日客流量。隱含層節點數目h選擇根據經驗公式來確定

其中：m和n分別是輸入層和輸出層節點的數目,a為[1, 10]內的調節常數。根據上述公式得到隱含層節點范圍為[3, 12], 將學習率定為0.1, 設定訓練次數上限為1 000次, 目標誤差為0.001, 隱含層激活函數采用tansig, 輸出層激活函數采用logsig。比較幾種網絡的訓練時間和誤差, 相關數據見表1。

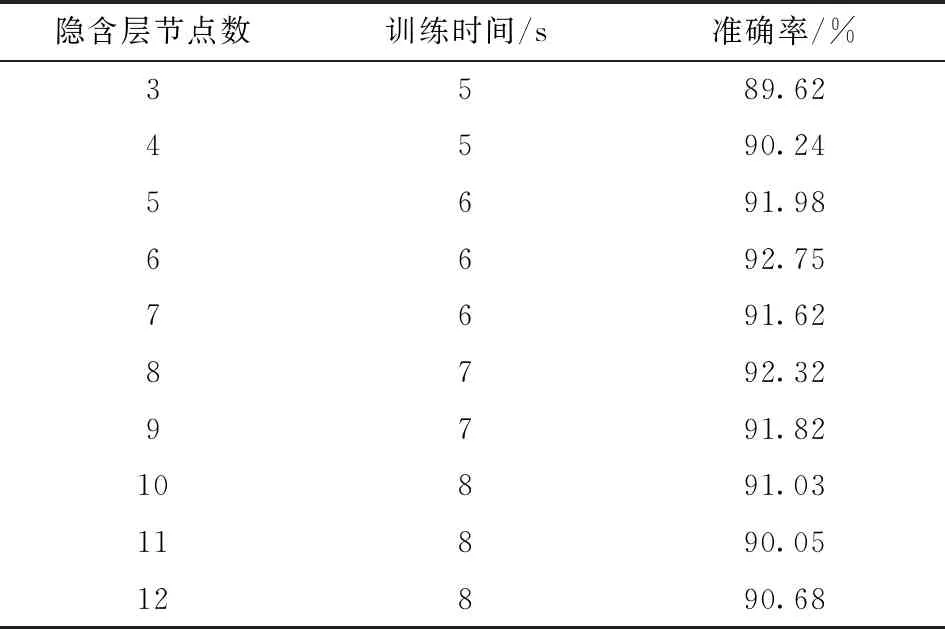
表1 節點數、訓練時間與準確率統計

可知, 隨著隱含層節點的增加, 訓練時間會逐漸增加, 準確率大致呈現一個先升后降的趨勢, 所以本文選取隱含層節點數為6, 其準確率最高, 而且訓練時間適中。

3.1.2 GA-BP神經網絡參數的確定 GA-BP神經網絡是在上述BP神經網絡模型的基礎上采用遺傳算法(GA)對BP神經網絡權值閾值的優化。在遺傳算法部分, 編碼方式為實數編碼, 種群規模為10, 最大進化代數為10, 交叉率為0.3, 變異率為0.5。

3.1.3 CGA-BP神經網絡參數的確定 在傳統遺傳算法中, 交叉率、 變異率為一固定值, 算法搜索速度慢, 容易早熟, 為了克服這一問題, 本文在GA-BP的基礎上用云模型的X條件云發生器生成交叉率和變異率, 具體見1.2節Pc、Pm的生成算法。在CGA-BP模型中, 當該染色體的適應度小于平均適應度時, 交叉率和變異率為一固定值, 根據上述對遺傳算法固定交叉率和變異率的設置, 令k3=0.3、k4=0.5，k1和k2為0～1間的常數, 圖3為k1、k2不同取值對模型準確率的影響, 其中不同顏色表示k1的取值。

圖3 k1、 k2對準確率的影響

模型準確率在97.5%～98.5%。k1、k2取值對模型的準確率有較大影響： 當k1=0.4、k2=0.6時, 模型準確率最低為97.56%; 當k1=0.3、k2=0.1時, 模型的準確率最大為98.47%, 兩者準確率相差0.91%。故本文設定k1=0.3,k2=0.1。

3.2 模型對比

根據上述對3個模型相關參數的分析, 可得各模型參數如表2所示。

表2 3個模型參數設置

應用重慶軌道交通3號線的客流數據對3個模型進行訓練, 將訓練好的模型用來預測重慶軌道交通2019年3月1—10日的客流, 其真實值與各模型的預測值如圖4所示。 可知, BP神經網絡模型的擬合能力較差, GA-BP神經網絡能夠比較準確地擬合數據, CGA-BP神經網絡能夠準確地反映出歷史數據的走向, 預測精度更高。

3個模型的平均絕對誤差(MAE)、 均方誤差(MSE)、 計算時間和準確率見表3。可知, GA-BP和CGA-BP的準確率較BP來說都有較大提高, 但是BP運行時間最短; CGA-BP的準確率在GA-BP的基礎上提高了1.9%, 同時運行時間減少了40%。兩者適應度曲線如圖5所示, 經云模型優化后的遺傳算法搜索速度及適應度值下降速度加快、 種群最佳平均適應度和終止進化代數減少。

圖5 GA-BP、 CGA-BP適應度曲線

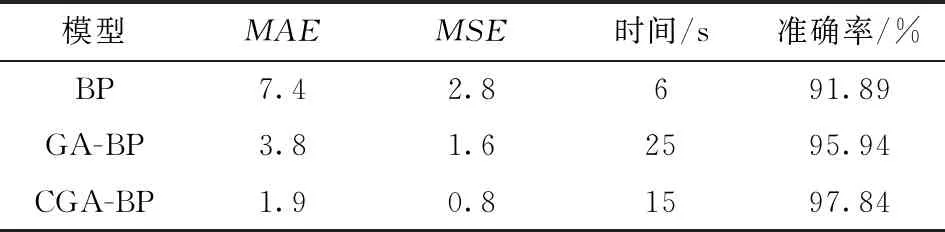
表3 不同模型評價

云遺傳算法優化后的BP神經網絡和遺傳算法優化的BP神經網絡訓練誤差變化如圖6所示。雖然在訓練誤差上都沒有達到目標誤差, 但CGA-BP比GA-BP的最佳訓練誤差更小, 在一定程度上提高了算法的準確度。

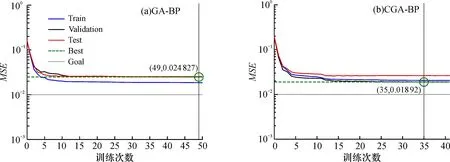
圖6 GA-BP(a)、 CGA-BP(b)訓練誤差

綜上, 3種模型求解結果均與真實值存在誤差, 但是云遺傳算法優化BP神經網絡(CGA-BP)比遺傳算法優化BP神經網絡(GA-BP)和BP神經網絡的預測精度都高, 這得益于云自適應遺傳算法中動態改變的交叉變異率, 使算法的初期能夠比較快地產生優秀個體, 算法的后期保護最優個體, 全局搜索能力增強。與GA-BP相比， 在提升精度的同時也減少了運行時間。

實驗表明: 本文設計的基于云遺傳算法優化BP神經網絡在全局搜索和收斂方面優于傳統BP神經網絡和遺傳算法優化BP神經網絡, 能夠保證軌道交通客流的預測精度。

4 結束語

針對云模型、 遺傳算法和BP神經網絡的的特點, 將三者結合起來建立云遺傳算法優化BP神經網絡的軌道客流預測模型。該模型既利用了云遺傳算法能并行計算且能快速、 全局搜索的優點, 解決了神經網絡固有的搜索速度慢且易陷入局部早熟的缺點， 又利用了神經網絡描述問題能力強、 對不完全信息具有良好的適應性的優點, 彌補了遺傳算法編碼困難的缺點。將此方法用于重慶市軌道交通3號線的日客流量預測, 與相同條件下的BP神經網絡模型、 遺傳算法優化BP神經網絡模型的預測結果進行對比發現, 基于云遺傳算法優化BP神經網絡的客流預測模型在預測精度上比BP神經網絡預測模型和遺傳算法優化BP神經網絡模型都更具優勢, 說明本文設計的預測方法是可行的。