基于數學學科核心素養的初中課題學習實踐與思考

霍明霞

基于數學六大核心素養制定的《義務教育數學學科課程標準》（2011年版），將數學課題學習這一內容逐步融入實際教學中，同時也通過實踐論的方式展示了數學的價值，引導學生對初中數學課題學習中的七個課題進行了學習與研究，啟發其思考，積累數學活動的經驗，為學生后續學習奠定基礎，培養他們的數學核心素養.在這里，筆者對人教版八年級上冊《數學》課題學習中的造橋選址問題進行教學實踐探索，挖掘其數學本質與數學思想，使學生在學習過程中獲得具有綜合性、階段性、持久性的數學能力，使得課題學習在現代教育中真正發揮其價值.

一、挖掘教材數學本質與數學思想，培養學生的數學抽象素養

人教版八年級上冊《數學》中提出的造橋選址問題：

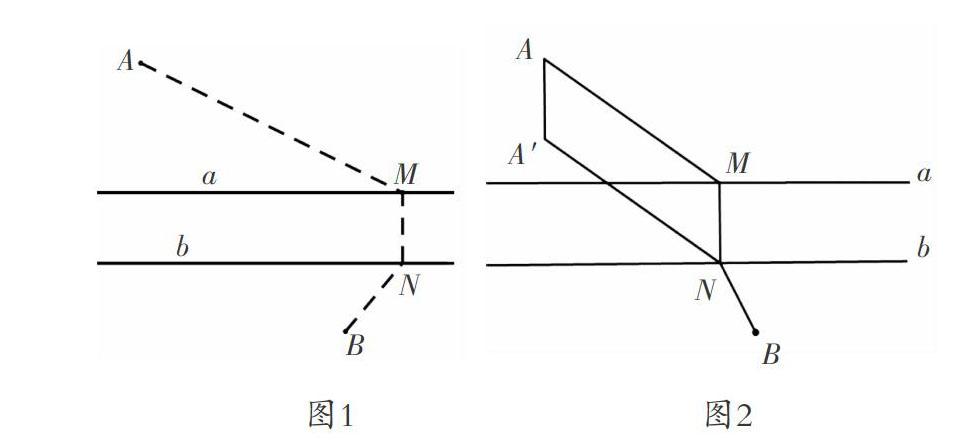
如圖1，A和B兩地在一條河的兩岸，現要在河上造一座橋MN.橋造在何處可使從A到B的路徑AMNB最短？（假定河的兩岸是平行的直線，橋要與河垂直）

如圖1，把河的兩岸看成兩條平行線a和b，N為直線b上的一個動點，MN垂直于直線b，交直線a于點M.這樣，上面的問題就可以轉化為下面的問題：當點N在直線b的什么位置時，AM+MN+NB最小？由于河岸寬度是固定的，因此當AM+NB最小時，AM+MN+NB最小.這樣，問題就進一步轉化為：當點N在直線b的什么位置時，AM+NB最小？

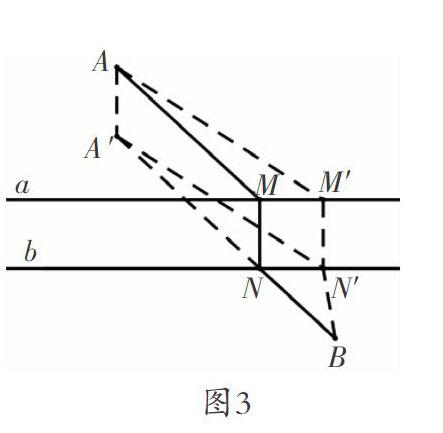
教材上解決這個問題的方法：如圖2，通過平移AM，將求AM，MN，NB三條線段和最短轉化為求兩條線段AM，NB的和最短.如圖3，其實就是將點A移動到點A′，將河的兩岸的兩點轉化為一條直線b兩側的兩個點，再利用兩點之間線段最短，連接A′，B兩點，從而找到造橋點N的位置.

通過對教材的研究，筆者幫助學生將造橋選址從實際背景中抽象出結構，提煉其數學本質，在數學思想的引領下，找到解決問題的數學方法，根據基本原理得到作圖的方法，從而解決最短路徑問題.但是，如何更好地運用平移的方法找到造橋的位置，教材給我們留下了廣闊的研究空間.

二、精心設計教學方案，啟發學生思維，培養學生的數學直觀想象素養

經過教學反思，筆者發現教材上的方法很好，但是學生卻很難想到，在轉化上較為復雜，不易形成思維通路.因此，結合學生思維最近發展區，筆者設計問題串，啟發學生思考，努力找到解決問題更好的方法.

問題一：如果河寬忽略不計，假設河為一條直線，點A與點B之間如何作圖才能找到造橋的選址點？

學生1回答：連接點A與點B，線段AB與代表河的直線的交點就是造橋的選址點.

問題二：請將圖1畫在一張白紙上，如何動手操作可以消除河的寬度？

學生2回答：如圖4，將這張紙沿直線a與直線b的中軸線對折.如圖5，使兩條平行河岸重合，點A與點B位于直線a（b）兩側.

問題三：此時，你能否作圖找到選址點？還原這張紙，你能找到線段MN嗎？

學生3回答：如圖6，連接點A與點B，線段AB與直線a（b）的交點就是造橋的選址點.如圖7，標注交點還原圖形后，連接直線a，b上標注的點M與點N，線段MN即為所求.

問題四：你找到最短路徑了嗎？請說出你找到的最短路徑，并說明理由.

學生4回答：找到了，如圖7，AM+MN+NB就是最短路徑.因為此時AM+NB=AB，兩點之間線段最短，MN是固定河寬，路徑AMNB就是最短路徑.

問題五：不能折紙時又如何作圖呢？

學生5回答：不能折紙消除河寬時，如圖8，可以通過將點A沿垂直于河岸方向向下平移河寬個單位到點A′，連接A′B，交直線b于點N，過點N作線段MN⊥a于點M，連接AM，MN，NB，所求即為最短路徑.

學生6回答：如圖9，還可以通過將點B沿垂直于河岸方向向上平移河寬個單位到點B′，連接B′A，交直線a于點M，過點M作線段MN⊥b于點N，連接AM，MN，NB，所求即為最短路徑.

學生7回答：如圖10，用兩種方法作圖得到的線段MN是一致的，我發現平移點A或是點B都可以找到造橋的選址點.

學生8回答：如圖11，過點B作BH⊥直線b于點H，將線段BH沿垂直于河岸的方向向上平移，得到線段B′H′⊥直線a于點H′.如圖12，連接AB′，交直線a于點M，再過點M作線段MN⊥直線b于點N.由此作圖得到造橋選址問題中的最短路徑AMNB.

教材上的方法，學生不容易想到，教師也不易設計教學，學生達不到這樣的認知水平，教學比較困難.教師可以創新教學方案，由問題串引導學生發現解決造橋選址問題的不同方法，探索這些方法的原理，通過作圖解決問題.教師再通過這些問題啟發學生思考.學生的思維能夠巧妙轉化，結合直觀想象，他們容易說出路徑最短的原理，通過思考再得出最佳作圖方法.

從教材解決造橋選址的方法，到折紙忽略河岸，平移點A或點B，再到直接平移垂線段BH到河對岸的線段B′H′，教師指導學生自主學習，學生承擔思考解法從繁到簡的任務，從而找到了最后一種易于操作的方法.可見，教學就是由教師引起、維持和促進學生學習的所有行為.

初中課題學習共七個內容，這七個內容密切聯系實際，綜合應用知識，以探索為主線，學習活動形式多種多樣.在上述以造橋選址問題為例，創設教學方案，啟發學生思維的教學實例中，教師由問題串引導學生找到忽略河寬的方法，教會學生思考問題的方法，挖掘數學的基本原理，找到作圖的最佳方法.在師生之間、生生之間持續互動的過程中，學生在思維上層層遞進，不僅積累了數學思維活動的經驗，而且學會思考，進而敢于思考，最后善于思考，最終提升了數學學科核心素養.

◇責任編輯 邱 艷◇