分數階p-Laplace算子相關的一個重排優化問題
邱 崇
(淮陰工學院 數理學院,江蘇 淮安 223001)
重排優化問題是指在某個可測函數所有重排函數組成的集合上的最優化問題,該問題有著豐富的物理背景,在彈性力學、流體力學、波動力學等領域都有重要應用。
19世紀著名物理學家 Thomson (Lord Kelvin) 曾提出如下一個平面流體力學問題:若某一區域流體的渦量場已知,在該渦量場所有可能的分布中能否找到某種分布使得該區域流體動能達到最大或最小?1989年Burton將該問題等價轉化為如下的重排優化問題:
max{E(g):g∈R(f)}和min{E(g):g∈R(f)}
其中f為區域Ω上已知的渦量場,g為f的一個重新分布或重排函數,E(g)表示渦量場為g時流體動能,R(f)為f的所有重排函數組成的集合。
利用泛函分析中鞍點定理等工具并結合重排函數集合的凸性等性質,Burton得到了以上兩個重排優化問題解的存在性,從而解決了Lord Kelvin的問題[1-2]。之后更多微分方程中的重排優化問題被提出并得到了廣泛的研究[3-6]。近年來,非局部算子相關的重排優化問題研究引起了越來越多的關注。
Qiu等[7]考慮了如下方程相關的重排優化問題,
其中Lθs是分數階Laplace型算子定義如下:
Lθsu(x)
得到了相應重排優化問題解的存在性等結果。已有文獻大多討論的是分數階Laplace算子相關的重排優化問題[8-13],而分數階p-Laplace算子相關的能量泛函重排優化問題尚未見報道。由于分數階p-Laplace算子不僅具有非局部性而且具有非線性性,因此其相關的重排優化問題研究需要克服更多困難。
本文將考慮如下的分數階Poisson方程
f(x)為某個可測函數。可以證明,對f(x)∈Lq(Ω)方程(1)具有唯一解,記為uf。
本文將討論如下的重排優化問題:

其中Φ(g):R(f)→R為能量泛函
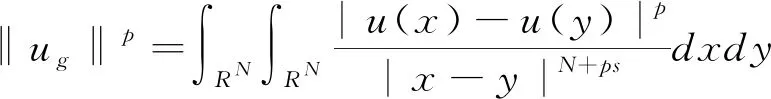
1 預備知識與常用引理
設f為有界光滑區域Ω?RN上的一個可測函數,其生成的重排函數空間R(f)是指由所有滿足條件:
meas({x∈Ω:g(x)≥a})=meas({x∈Ω:f(x)≥a}),?a∈R
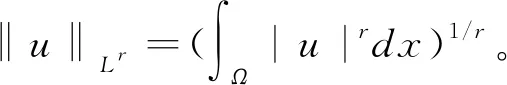
并記:
Ws,p(RN)={u∈Lp(RN):[u]s,p<∞}
為以:
為范數的分數階Sobolev空間,其中0 W0s,p(Ω)={u∈Ws,p(RN):u≡0,x∈RN 定義1 稱u∈W0s,p(Ω)為分數階Poisson方程(1)的一個解,如果 注意到,方程(1)對應的能量泛函If:W0s,p(Ω)→R為: 本文中常用的引理如下: 引理2 (Burton[2]引理2.1)若f∈Lp(Ω),1≤p<∞,則對任意的g∈R(f)都有g∈Lp(Ω)且‖g‖Lp=‖f‖Lp。 其中1 由于p≥2,所以‖u‖→∞時一定有If(u)→∞。因此泛函If是強制的。 =If(v) 因此,綜上可得uf是方程(1)的一個基態解。 下面證明uf是分數階Poisson方程(1)的唯一解。 若記uf(x,y)=uf(x)-uf(y),wf(x,y)=wf(x)-wf(y),v(x,y)=v(x)-v(y)則上兩式即為 相減可得 特別地,令v=uf-wf,則 由Clarkson不等式,可得 (|uf(x,y)|p-2uf(x,y)-|wf(x,y)|p-2wf(x,y))(uf(x,y)-wf(x,y))≥C|uf(x,y)-wf(x,y)|p 所以, 矛盾。因此是方程(1)的唯一解。證畢。 根據引理2,‖g‖Lq=‖f‖Lq,由上式即可推知A一定是有限數。 任取{gi}?R(f)為一個極小化點列,即 再結合Holder不等式可推出 再結合(4),得到 由性質1, 本文研究了一類非局部算子即分數階p-Laplace算子相關的一個能量泛函重排優化問題。該算子不僅是非局部算子而且具有非線性性。首先,利用合適的變分框架并使用全局極小原理得到分數階Poisson 方程的基態解。然后,通過反證法并結合Clarkson不等式得到方程解的唯一性。之后,使用重排優化理論研究了相關的一個能量泛函極小重排優化問題。最后,通過分析極小化序列的性質證明了該重排優化問題的可解性。目前尚未有分數階p-Laplace算子相關的能量泛函重排優化問題文獻發表,因此本文的結果是新的。更多非局部算子相關的重排優化問題研究尚待今后進一步深入開展。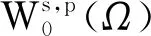
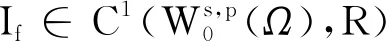
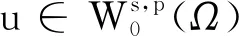
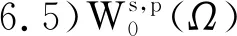
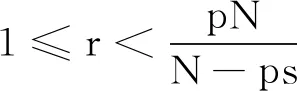
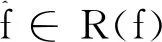
3 分數階Poisson方程(1)的基態解
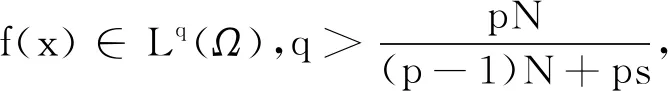
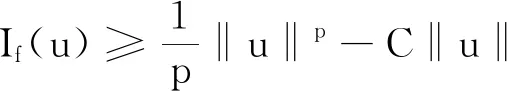
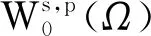
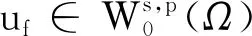
4 最優化問題(Opt)的極小點


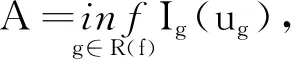
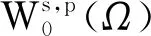
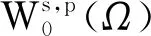
5 結論

