Leg-by-leg機動條件下純方位跟蹤的觀測站機動策略

奚 暢,蔡志明,袁 駿

(海軍工程大學電子工程學院,湖北 武漢 430000)

0 引 言

純方位目標被動跟蹤又稱純方位目標運動分析,指利用被動觀測的目標方位信息估計目標運動參數的過程。由于方位信息是目標運動參數的不完全描述,目標可觀測的必要非充分條件是觀測站進行機動。為了使可觀測性盡量強,需選擇合適的觀測站機動策略,這關系到目標狀態估計的收斂率、收斂速度、估計精度、濾波穩定性等性能。

Fisher信息矩陣(Fisher information matrix,FIM)是一次觀測所能提供的關于未知多維參數的信息量期望值的一種度量,是計算目標狀態估計誤差Cramer-Rao下界(Cramer-Rao lower bound,CRLB)、幾何定位散布精度(geometric dilution of precision,GDOP)等指標的基礎。由于FIM刻畫了估計系統理論上最佳可達性能,以FIM行列式最大作為最優機動策略的性能指標是主流的研究方向[1-4]。基于FIM的機動策略設計方法需要在觀測站機動前計算各種機動方案對應的觀測過程中累積的FIM,而FIM計算所需的目標距離信息在機動前未知,對此問題的解決方法分為兩類。

第一類方法是邊估計運動參數-邊優化觀測站軌跡,即利用最新估計的目標距離計算FIM,得到局部最優機動策略。Liu[1]用最優控制論中的Hamilton-Jacobi方程求解觀測平臺的最優軌跡,得到對目標的追擊曲線。Hammel[2]在拖線陣航向變化小于20次的限制條件下,提出最優軌跡的近似數值解法。文獻[5]給出了位變率最大指標下的機動策略,并分析了目標各種運動情況下的最優軌線特性。文獻[6]基于FIM行列式最大指標和方位變化率最大指標,結合貪心算法提出“一步最優”的機動軌跡。應用變分法和極值原理,文獻[7]得到Gram矩陣最大和FIM行列式增量最大兩種指標條件下最優軌跡方程。當利用擴展卡爾曼濾波進行跟蹤時,文獻[8]根據CRLB遞推公式[9],以CRLB最小(FIM行列式最大)為準則設計折線形的拖船機動軌跡。此類方法的缺陷在于觀測站需要利用局部最優策略進行多次機動,在實際應用場景中難以實施。

第二類方法是基于觀測站leg-by-leg機動模式,得到與目標方位相關的轉向規則。Leg-by-leg機動是由兩個勻速直行段組成的折線形機動,希望利用一次轉向達到全局最優,是一種易于實施的機動模式。文獻[10]假設leg-by-leg機動中的轉向可瞬間完成,通過討論若干情景下的可觀測性問題,可提出系統可觀測的必要條件。Le[11-13]采用多重線性代數的方法,利用兩個直行段的目標方位變化率得到FIM行列式的近似值,證明觀測者的最優機動策略應是在最大和最小位變率間跳變的bang-bang控制。Fawcett[14-15]假設目標距離較遠,利用轉向前后目標初始方位線及其垂線方向的相對速度變化近似計算FIM,認為觀測站的最優轉向角度應是初始方位的垂直方向。此類方法的缺陷在于只能得到與目標方位有關的某種轉向規則,無法計算FIM的解析值。

在實際的目標運動分析場景下,希望通過一次觀測站轉向機動,以最短時間實現滿足某種精度要求的目標運動狀態估計,機動策略設計的關鍵在于觀測站機動前計算完整觀測過程中累積的FIM。為了在leg1段計算各機動方案的FIM,以便根據參數估計精度和估計時間的要求設計機動策略,一方面,對于勻速直線運動的目標,假設相對速度在x軸、y軸的分量與初始距離的比值已知,且目標速度范圍已知,通過假設目標速度對目標初始狀態進行粗估,提出了使歸一化初始距離粗估誤差最小的目標速度假設方法;另一方面,對FIM行列式進行近似及多項式展開,提出了通過控制前后leg段比例以減小狀態粗估誤差對FIM行列式的影響。

1 系統模型

對于含有角度測量的目標運動分析,笛卡爾坐標系下的目標狀態估計存在方差發散和結果不穩定的現象。修正極坐標系[16]將狀態向量中的可觀測部分和不可觀測部分解耦,在濾波過程中避免了病態方差矩陣,增加了濾波穩定性,其結果漸近無偏[17-19]。

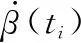
(1)

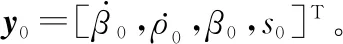
設ax(ti)、ay(ti)分別為目標相對觀測站在x軸、y軸方向的加速度,以初始時刻目標和觀測站的狀態為基準,相對加速度導致的相對速度及相對位置變化為

(2)

式中:w1(ti)和w2(ti)分別表示x軸、y軸方向的相對速度變化；w3(ti)和w4(ti)分別表示x軸、y軸方向的相對位置變化。設VR(ti)和VB(ti)分別為目標初始方位方向、目標初始方位垂直方向上的相對速度變化,AR(ti)和AB(ti)分別為目標初始方位方向、目標初始方位垂直方向上的相對位置變化,則有

(3)

定義中間變量:

(4)

將目標狀態向量y(ti)表示為初始時刻目標狀態向量y(t0)的函數,可得修正極坐標系下[16]的狀態方程:

(5)

純方位測量情況下,觀測量是目標狀態向量中的元素,測量方程可表示為線性形式:

(6)

式中:η(ti)表示量測噪聲,服從均值為0、方差為R的獨立高斯分布。

2 Leg-by-leg機動模式下的FIM計算

Leg-by-leg機動由兩個運動方向不同的勻速直行段組成,又稱轉向機動、折線機動、兩段直航式機動,是一種易于實施的機動模式,適用于船艇等機動性欠佳的觀測載體。按照時間先后順序,兩個勻速直行段分別稱為leg1段和leg2段。實際場景下,觀測站在搜索目標時的工況是勻速直線運動,發現目標后希望盡快確定其位置,因此通常將發現目標的時刻作為leg1段的起始時刻。

假設目標保持勻速直線運動,觀測站進行leg-by-leg機動,轉向時刻為ta且瞬時完成轉向,leg2段結束時刻為tk,則相對加速度由觀測站轉向產生,用ar、ab分別表示目標初始方位方向、目標初始方位垂直方向上轉向前后的觀測站速度變化,則有

(7)

(8)

(9)

(10)

將式(4)代入式(5)可得ti時刻的目標方位值:

(11)

由定義可得對初始時刻目標狀態的FIM:

(12)

式中:i為采樣序號,Ji(y0)為雅克比矩陣:

(13)

(14)

對于leg-by-leg機動模式,在笛卡爾坐標系下用傳統方法計算FIM[20-21]需利用各采樣時刻的目標距離值和方位值,在轉向之前無法獲得轉向后的相關參數,因而無法對轉向策略提出指導。假設轉向可瞬時完成,在修正極坐標系下計算FIM只需初始時刻的目標狀態和觀測站轉向前后的速度變化量,可在轉向前計算各機動方案對應的觀測過程中累積的FIM,進而根據參數估計精度和估計時間的要求設計合適的機動策略。

3 目標初始狀態粗估

3.1 初始狀態粗估方法

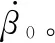
(15)

設vo為觀測站速度,vox、voy分別為觀測站速度在x軸和y軸的分量,θ為目標航向,vt為目標速度,vtx、vty分別為目標速度在x軸和y軸的分量,vrx/r0、vry/r0可寫為

(16)

(17)

3.2 目標速度假設方法

假設可以準確測量目標方位測量并估計vrx/r0、vry/r0,初始時刻目標狀態向量中只有距離的估計存在誤差,目標速度的假設對于初始距離估計誤差起關鍵作用。根據式(17)可得初始距離粗估誤差:

(18)

由式(18)可知,初始距離粗估誤差與目標真實初始距離成正比,與相對運動速度成反比,與初始距離粗估誤差正相關。對于目標真實速度較小的情況與目標真實速度較大的情況,相同的目標速度假設誤差造成的影響不同,因此將目標速度假設為目標速度范圍的中點無法得到統計意義上最小的初始距離粗估誤差。

不失一般性,假設觀測站航向為0°,對于目標假設速度為vt,h的情況,定義歸一化的初始距離粗估誤差為

(19)

對于目標速度和運動方向滿足一定概率分布的情況,目標速度假設值vt,h應使g(vt,θ)的期望最小。

由式(17)可知,目標速度假設值vt,h需滿足

(20)

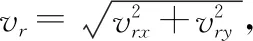
(21)

即目標速度假設值vt,h應不小于觀測站速度在相對運動垂直方向的分量。

根據目標類型和跟蹤場景,可知目標的速度范圍為[vt,min,vt,max]。如果目標最小速度vt,min大于等于觀測站速度vo,目標速度假設值vt,h在[vt,min,vt,max]范圍內取值可保證式(21)成立。假設目標速度vt服從[vt,min,vt,max]范圍內的均勻分布,目標運動方向θ服從[0,360°)范圍內的均勻分布,vt和θ的概率密度函數分別為

(22)

由于變量vt和θ彼此獨立,可得聯合概率密度函數:

(23)

在[vt,min,vt,max]范圍內按固定間隔取若干離散值,依次將所取值作為目標速度假設值vt,h,計算歸一化距離粗估誤差的期望:

(24)

選擇使歸一化距離粗估誤差期望最小的目標速度假設值,代入式(17)完成初始距離粗估。

如果目標最小速度vt,min小于觀測站速度vo,目標速度假設值vt,h須在[voxvry/r0-voyvrx/r0,vt,max]范圍內取值以滿足式(21)成立,voxvry/r0-voyvrx/r0即為目標速度假設下限。由于目標速度假設下限與觀測站速度和相對速度方向相關,無法解析地計算歸一化距離粗估誤差的期望,需要對于各種目標速度假設下限的情況,分別通過蒙特卡羅仿真計算歸一化距離粗估誤差期望隨目標速度假設值變化情況。目標運動分析過程中,利用估計的vrx/r0、vry/r0計算目標速度假設下限,選擇此情況下使誤差期望最小的目標速度假設值,代入式(17)完成初始距離粗估。

4 減小距離粗估誤差影響

第3節致力于減小初始距離粗估誤差,本節將討論如何減小誤差對FIM行列式的影響。首先計算FIM行列式的解析表達式,式(11)～式(14)較為復雜無法展開,需對其進行簡化。利用反正切函數的泰勒級數,對式(11)進行一階展開可得

(25)

式(25)對初始時刻狀態向量求偏導,可得雅克比矩陣中的元素,如下所示：

(26)

利用分式的泰勒級數,對式(26)進行一階展開得到

(27)

(28)

--------------------

設采樣間隔為Δt,將式(12)中的求和變為積分的形式:

(29)

對于兩個積分區間,將式(9)和式(10)代入式(28)得到雅克比矩陣Ji(y0),利用基于計算機代數系統的Mathematica軟件對式(29)進行積分運算,得到的FIM行列式是一個包含2 460個分項的多項式,初始距離r0以其倒數s0=1/r0的形式在式中體現。多項式各項中s0的階數從0階到10階不等,以s0的階數作為索引,將FIM行列式表示為

(30)

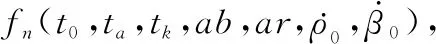
(31)

式中:tk-ta表示leg2段的時長。因此leg2段時間越短,高階s0項對結果影響越小,初始距離粗估值對FIM行列式的影響越小。用Ra=(ta-t0)/(tk-t0)∈[0,1]表示leg1段占leg-by-leg機動總時長的比例,leg-by-leg機動總時長一定時,增大Ra可減小初始距離粗估誤差的影響。但是,Ra=1表示觀測站勻速直行未發生機動,Ra接近1會造成真實的|FIM(y0)|較小,不利于目標參數估計。

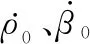
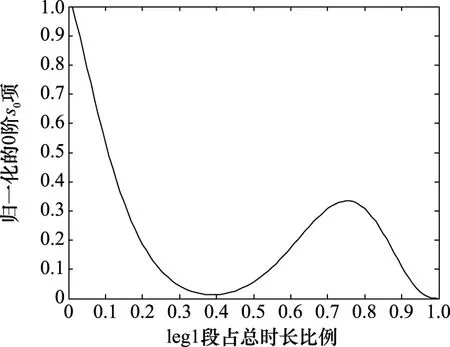
圖1 歸一化的0階s0項變化情況Fig.1 Change of normalized zero-order term of s0

由圖1可知,Ra處于[0.7,0.8]范圍內時歸一化的0階s0項相對較大。因此,leg-by-leg機動總時長一定時,應對于[0.7,0.8]范圍內的各種Ra和[0,360°)范圍內的各種觀測站轉向角度計算FIM行列式,根據參數估計精度和估計時間的要求設計最優機動策略。

5 實驗與結果分析

5.1 目標速度假設方法

在水下目標跟蹤場景下進行討論,假設觀測站速度為4 kn,觀測站運動方向為0°,目標速度服從[5,10]kn范圍內的均勻分布,目標運動方向服從[0,360°)范圍內的均勻分布。由于觀測站速度小于目標最小速度,目標速度假設值vt,h可以在[5,10]kn范圍內取值,對于[5,10]kn范圍內間隔0.2 kn變化的若干種目標速度假設情況,依次利用式(24)計算歸一化距離粗估誤差期望的理論值,利用106次蒙特卡羅仿真計算歸一化距離粗估誤差期望的仿真值,結果如圖2所示。

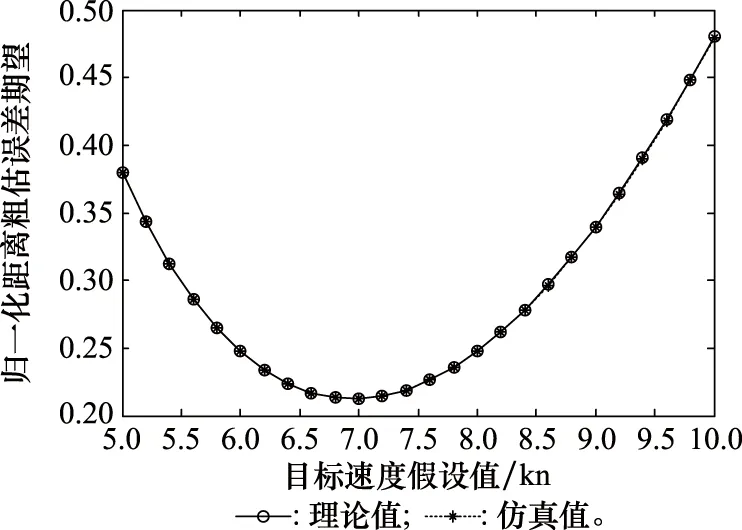
圖2 歸一化距離粗估誤差(目標速度假設下限固定)Fig.2 Normalized distance rough estimation error (lower bound of target velocity assumption is fixed)

由圖2可知,目標速度假設值為7 kn時歸一化距離粗估誤差期望達到最小,對于上述假設的目標速度和目標速度范圍,應令目標距離假設值為7 kn。歸一化距離粗估誤差期望的理論值和蒙特卡羅仿真值基本一致,可認為兩種方法等效,無法解析計算粗估誤差期望時采用蒙特卡羅仿真方法進行替代是合理的。

假設觀測站速度為4 kn,觀測站運動方向為0°,目標速度服從[0,10]kn范圍內的均勻分布,目標運動方向服從[0,360°)范圍內的均勻分布。由于觀測站速度大于目標最小速度,需要對于各種可能的目標速度假設下限,分別計算使歸一化距離粗估誤差期望最小的目標速度假設值。間隔1 kn設置若干種目標速度假設下限情況,通過106次蒙特卡羅仿真計算各種目標速度假設下限情況下,歸一化距離粗估誤差期望隨目標速度假設值的變化,結果如圖3所示。

目標運動分析過程中,可根據實際計算的目標速度假設下限,利用圖3選擇使誤差平均值最小的目標速度假設值。例如,圖3中目標速度假設下限為1 kn情況下,目標速度假設值等于1.2 kn時歸一化距離粗估誤差期望最小,因此如果在實際應用場景下計算的目標速度假設下限接近1 kn,應令目標速度假設值為1.2 kn。為方便繪圖顯示及說明,上述仿真以1 kn間隔設置目標速度假設下限情況,在實際應用中可以采用更小的間隔以獲得更精確的結果。

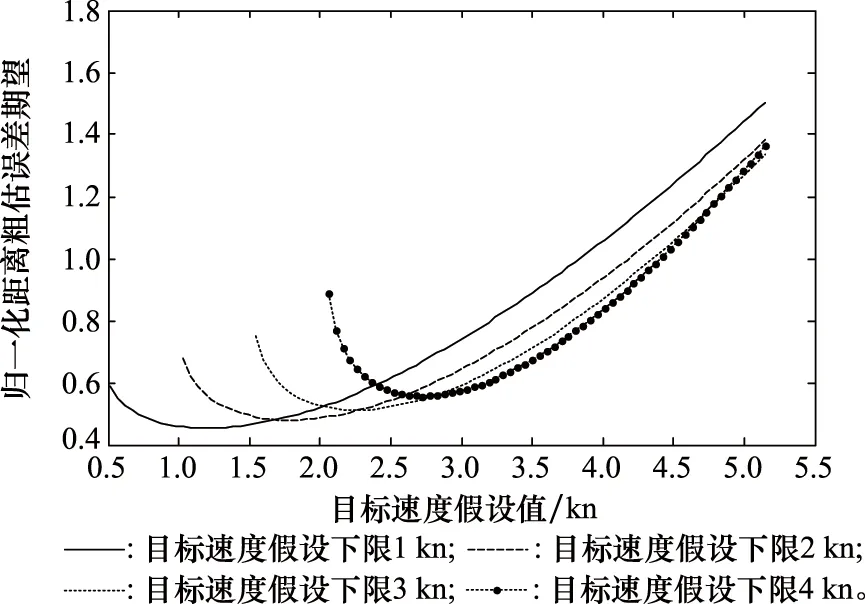
圖3 歸一化距離粗估誤差(目標速度假設下限不固定)Fig.3 Normalized distance rough estimation error (lower bound of target velocity assumption is not fixed)

由圖2和圖3可知,觀測站速度為4 kn,目標速度在[0,10]kn范圍內時,利用第3節方法的歸一化距離粗估誤差期望小于0.6。

5.2 leg比例對FIM的影響

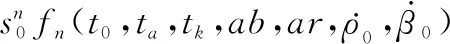
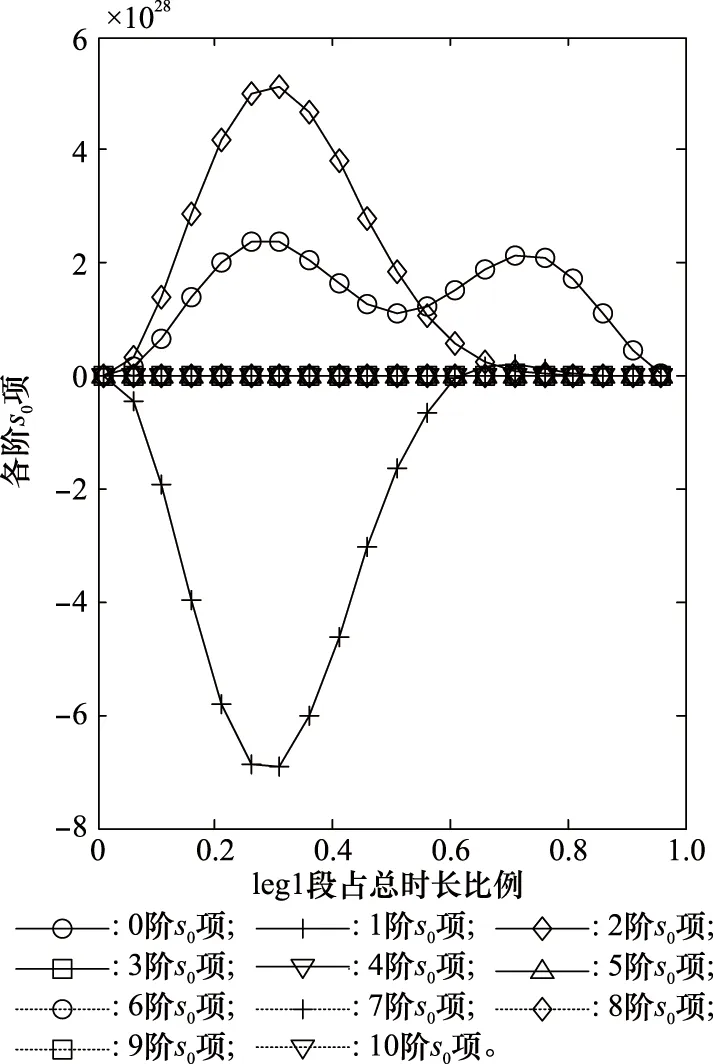
圖4 各階s0項變化情況Fig.4 Change of every order term of s0

由圖4可知,s0階數小于等于2的項顯著大于其他項,FIM行列式主要由此3項決定。隨著Ra增大,s0階數大于0的項在Ra>0.3后逐漸收斂至0,s0階數為0的項在Ra∈[0.7,0.8]時達到極大值,與圖1結論一致。

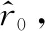
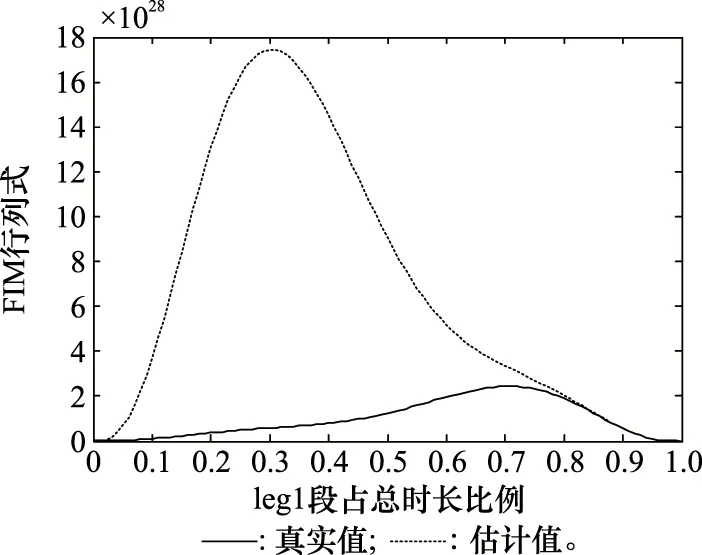
圖5 FIM行列式隨Ra變化情況Fig.5 Change of FIM determinant with Ra

由圖5可知,Ra越大,FIM行列式的估計值越接近真實值,表示FIM行列式受目標粗估誤差影響越小,Ra接近1時真實值與估計值基本吻合但FIM行列式接近0,與理論分析結果一致。

5.3 FIM估計精度驗證

設觀測站速度為6 kn,leg1段觀測站航向為0°,目標初始方位為-30°,目標初始距離為10 km,目標速度為4 kn,目標航向為120°,leg-by-leg機動總時長為600 s,leg1段占總時長的比例Ra=0.8,方位測量方差為(0.5°)2,測量間隔為10 s。認為目標速度范圍為[0,10]kn,對于不同的轉向角度即leg2段運動方向,利用真實目標初始距離計算FIM行列式真實值,用目標初始距離粗估值計算FIM行列式估計值,結果如圖6所示。

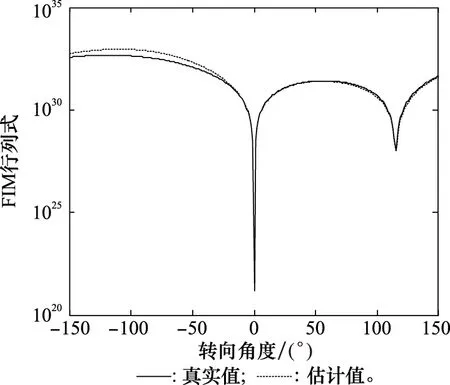
圖6 FIM行列式隨轉向角度變化情況Fig.6 Change of FIM determinant with steering angle

利用FIM行列式真實值和估計值可得FIM行列式估計誤差,除以FIM行列式真實值可得相對估計誤差,將相對估計誤差在轉向角度維度取平均得到FIM行列式相對估計誤差均值。對圖6所示結果進一步處理可得,該機動場景假設下FIM行列式相對估計誤差均值為0.37。

假設一種典型的水下目標跟蹤場景,設觀測站速度為6 kn,leg1段觀測站航向為0°,leg-by-leg機動總時長為600 s,測量間隔為10 s,方位測量方差為(0.5°)2。目標初始方位范圍為[0,360°),目標初始距離范圍為[10,50]km,目標速度范圍為[0,10]kn,目標航向范圍為[0,360°),leg1段占總時長的比例Ra范圍為[0.7,0.8],上述目標運動參數在各自范圍內服從均勻分布。進行103次蒙特卡羅仿真,每次仿真時目標運動參數隨機取值,利用與圖6相同的方法計算FIM行列式相對估計誤差均值,得到一次蒙特卡羅仿真的結果,將103次蒙特卡羅仿真的結果由小到大排序,如圖7所示。由于初始距離粗估誤差與相對運動速度成反比,相對運動速度極小時距離粗估誤差極大,導致相對估計誤差出現極大值。由圖7分析可知,若以FIM行列式相對估計誤差小于0.2作為有效估計準則,則有效估計概率為76.7%,有效估計情況下平均的相對估計誤差為0.12。因此,認為在典型的水下目標跟蹤場景下,利用本文方法可以較為有效地計算FIM,進而實現機動策略設計。

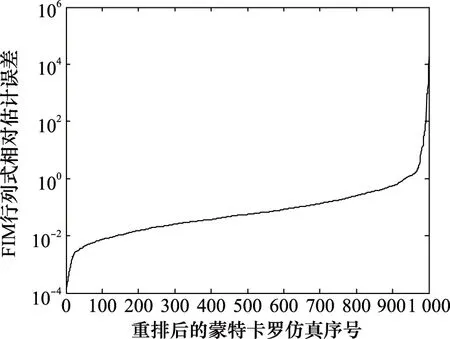
圖7 FIM行列式相對估計誤差Fig.7 Relative estimation error of FIM determinant

6 結 論

對于觀測站leg-by-leg機動模式,為了在leg1段計算各機動方案的FIM,進而根據參數估計精度和估計時間的要求設計機動策略,從粗估目標初始距離和減小粗估誤差對FIM行列式影響兩方面著手開展研究。一方面,對于勻速直線運動的目標,假設相對速度在x軸、y軸的分量與初始距離的比值已知且目標速度范圍已知,通過假設目標速度實現目標初始狀態粗估,提出了使歸一化初始距離粗估誤差最小的目標速度假設方法;另一方面,對FIM行列式進行近似及多項式展開,提出了通過控制前后leg段比例以減小狀態粗估誤差對FIM行列式的影響。仿真結果表明:

(1)計算目標速度假設值時,解析方法和蒙特卡羅仿真方法等效,觀測站速度為4 kn,目標速度在[0,10]kn范圍內時,歸一化距離粗估誤差期望小于0.6;

(2)leg1段占總時長的比例在[0.7,0.8]范圍內時,FIM行列式受目標初始距離粗估誤差影響較小,且避免真實的FIM行列式趨近于0;

(3)對于典型的水下目標跟蹤場景,FIM行列式的有效估計概率為76.7%,平均的相對估計誤差為0.12,可有效地設計觀測站機動策略。

本文方法的缺陷在于需要利用相對速度在x軸、y軸的分量與初始距離比值。后續研究內容包括:非瞬時轉向情況下轉彎半徑對于FIM計算結果的影響;如何更準確地粗估目標初始狀態;相對速度在x軸、y軸的分量與初始距離比值的估計誤差對FIM計算結果的影響。