基于單快拍空間平滑的多伯努利DOA跟蹤算法
吳孫勇,鄒寶紅,薛秋條,孫希延,王 力
(1.桂林電子科技大學數學與計算科學學院,廣西 桂林 541004;2.廣西信息科學實驗中心,廣西 桂林 541004)
0 引 言
陣列信號處理技術廣泛應用于移動定位、電子偵察、雷達跟蹤、聲吶系統等領域,而波達方向(direction of arrival,DOA)估計問題是陣列信號處理中的重點研究內容之一。經典的DOA參數估計算法一般都屬于靜態信號源的DOA估計,如基于波束形成的DOA估計算法[1]、多重信號分類[2-4]、旋轉不變子空間技術[5]等算法。然而在實際場景中,信號源通常是運動的,采用該類算法進行DOA估計需要用多快拍批處理方式對接收矩陣進行處理,計算量大,無法滿足DOA的動態實時跟蹤。
目前,關于動態 DOA跟蹤類算法的研究方法主要包括基于子空間類方法和基于狀態濾波類方法。基于子空間類的跟蹤算法[6-9],如投影近似子空間跟蹤(projection approximation subspace tracking,PAST)算法[6-7]、緊縮PAST(PAST deflation,PASTD)算法[8]、雙迭代奇異值分解算法[9]等,此類算法都是通過構造代價函數采用遞歸最小二乘法進行子空間更新,從而實現DOA跟蹤。但是由于這類算法都考慮了一個固定的DOA數目場景,無法實現跟蹤數目時變的DOA信號,且跟蹤快速運動目標時性能下降。而狀態濾波類方法采用基于貝葉斯框架下的粒子濾波算法遞歸估計動態系統的狀態,被廣泛的應用到DOA跟蹤問題[10-13]。文獻[10]提出一種基于改進粒子濾波算法的陣列單通道機動目標DOA跟蹤方法,文獻[11]提出單機動目標DOA跟蹤粒子濾波算法,將多重信號分類(multiple signal classification,MUSIC)空間譜代替粒子濾波的似然函數,結果表明基于粒子濾波的跟蹤算法優于傳統的子空間類跟蹤算法。但該類算法也無法實現跟蹤信號源數目時變的DOA。
實際情況中,跟蹤的信號源數目可能是時變的,如潛艇跟蹤、移動定位等。Mathler提出的有限集統計學理論(finite set statistics theory,FISST)的概念,將多目標的狀態和量測建模為隨機有限集(random finite set,RFS),構建貝葉斯框架下的RFS濾波算法[14-16],為目標數目時變的跟蹤問題提供了一種新的思路。目前,RFS濾波器的兩個成熟分支是概率假設密度(probability hypothesis density,PHD)、勢PHD(cardinalized PHD,CPHD)和多伯努利濾波器。由于這些理論中所得量測的前提假設是任何量測都是由最多單個目標產生,而陣列信號的量測不符合隨機有限集理論下的“標準量測”。針對這個問題學者們提出多種方法解決[17-19],文獻[17]提出了一種基于相控陣觀測的多目標DOA跟蹤的檢測前跟蹤濾波器,采用一個新的標記泊松點過程(marked poisson point process,MPP)模型并推導出MPP-PHD濾波器DOA跟蹤的遞歸公式。文獻[18]推導了具有高斯噪聲的疊加傳感器的PHD和CPHD濾波器的可近似處理計算。文獻[19]提出一種適用于脈沖噪聲的多元擴展目標的近似CPHD濾波器DOA跟蹤算法。文獻[20]基于隨機有限集框架提出基于協方差的多目標DOA跟蹤問題方法,該方法允許接收陣列量測直接進入CPHD濾波器中,用一個復雜的Wishart隨機矩陣表示其似然分布,從而跟蹤未知時變DOA。其中PHD、CPHD粒子濾波器傳遞后驗分布的一階矩和勢分布,與PHD、CPHD粒子濾波器相比,多目標多伯努利(multi-target multi-Bernoulli,MeMBer)濾波器[21-28]將每個目標建模為伯努利RFS,并傳遞服從多伯努利分布的近似后驗多目標密度參數,且在一段時間內維持許多伯努利分量,每個分量都是一個潛在的目標,使得MeMBer濾波器能更有效地對時變多目標進行跟蹤。Choppala[24]等人提出將 MUSIC 譜函數作為MeMBer的偽似然函數,對相控陣列進行有效的DOA 跟蹤。在文獻[25]中研究了在監控中隨機出現或消失的單一運動源的聯合檢測和DOA跟蹤問題,提出了一種用于跟蹤隨機開/關的單動態系統的檢測前跟蹤伯努利濾波器。文獻[27]提出一種基于無跡變換MeMBer濾波框架下的多源到達方向跟蹤算法。這類多伯努利DOA跟蹤算法中,每個時刻都需要多快拍數據構造較為精準的陣列協方差矩陣的估計陣,再采用MUSIC偽似然函數直接對傳感器信號進行濾波。實際應用中我們難以在瞬時間內獲得多個平穩獨立的快拍數據。
針對以上問題,本文提出了一種新的單快拍情況下粒子濾波類的跟蹤算法—基于空間平滑的MeMBer(spatial smoothing with MeMBer,SS-MeMBer)跟蹤算法。由于每時刻獲取的單快拍數據難以直接應用到多伯努利濾波器中計算量測似然函數,因此本文利用空間平滑方法對量測進行處理,用平滑后的數據代替協方差矩陣,進行奇異值分解,用MUSIC空間譜函數作為多伯努利的偽似然函數。該算法首先建立均勻線陣的量測模型,并以目標運動模型作為狀態模型對目標狀態和數目進行預測。然后,在更新階段利用平滑后的數據代替協方差矩陣,進行奇異值分解,構造噪聲子空間,用MUSIC空間譜函數作為多伯努利的偽似然函數,最后根據多伯努利濾波器理論對目標狀態進行遞歸跟蹤,并進行狀態提取。該算法的主要優點是在每時刻獲取到的單快拍量測信息時,可以準確跟蹤信號源數目時變和狀態未知的DOA。
1 問題描述
1.1 隨機有限集理論
假設k時刻單個目標狀態為xk,則狀態轉移模型和量測模型分別為
(1)
式中:fk,hk分別表示狀態轉移函數和量測函數;nk,wk分別表示為過程噪聲和量測噪聲。
在k時刻有Mk個目標xk,1,xk,2,…,xk,Mk(xk,i∈Rnx)和Nk個量測zk,1,zk,2,…,zk,Nk(zk,i∈Rnz),其中nx,nz分別表示狀態和量測的維度。把k時刻目標狀態和量測的有限集分別表示為
(2)
根據狀態空間F(X)和量測空間F(Z)可以建立多目標貝葉斯濾波器。假設πk(·|Z1:k)表示k時刻的多目標后驗密度,根據文獻[22]隨時間貝葉斯遞歸傳播多目標后驗密度為
πk|k-1(Xk|Z1:k-1)=
(3)
πk(Xk|Z1:k)=
(4)
式中:積分項為RFS變量X的FISST集積分;πk|k-1(·|·)為多目標的后驗概率密度函數;fk|k-1(·|·)表示多目標轉移概率;gk(·|·)是多目標似然函數。
1.2 多伯努利濾波器
(5)
根據貝葉斯理論,MeMBer濾波器估計目標狀態分為預測和更新兩個階段,其中預測過程為
(6)
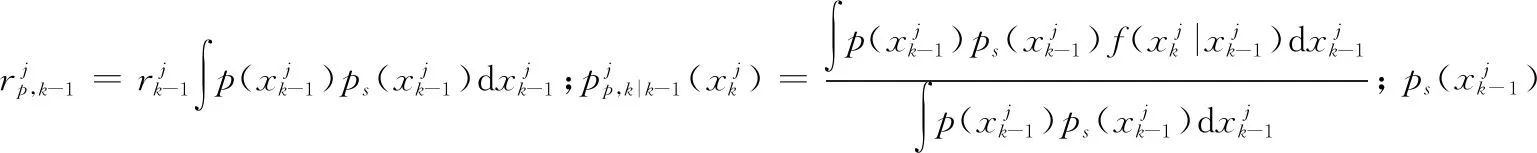
且k時刻多伯努利隨機有限集更新為
(7)
式中:
(8)
(9)
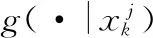
1.3 陣列模型
考慮由M個全向陣元組成的等距線陣,陣元間距為d≤λ/2(λ是入射信號波長),現有K個遠場窄帶信源分別以角度θi(i=1,2,…,K)入射接收線陣。以陣元1為參考陣元,則第m個陣元的輸出信號可表示為
(10)
式中:si(t)為第i個信號的復包絡;nm(t)為第m個陣元接收到的理想高斯白噪聲。
則陣列接收的數據可進一步表示為
Y(t)=[y1(t),y2(t),…,yM(t)]T=A(θ)S(t)+N(t)
(11)
式中:A(θ)=[a(θ1),a(θ2),…,a(θK)]為M×K維陣列流形矩陣;a(θi)=[1,e-j2πdsinθi/λ,…,e-j2πd(M-1)sinθi/λ]為第i個信源方向矢量,陣列高斯白噪聲矢量為N(t)=[n1(t),n2(t),…,nM(t)]T,且滿足:
(12)
假設信號與噪聲不相關,接收陣列的協方差矩陣為
R=E[Y(t)YH(t)]=A(θ)RSA(θ)H+RN
(13)
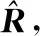
(14)
2 空間平滑多伯努利DOA跟蹤算法
本節通過在傳感器陣列中采樣單快拍量測數據,針對時變DOA跟蹤問題,給出SS-MeMBer DOA跟蹤算法理論。
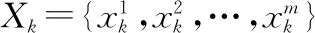
(15)
式中:vk為高斯白噪聲;Fk是狀態轉移矩陣。
假設在k時刻M個全向陣元接收的陣列信號為,則傳感器量測模型為
Yk=[y1(k),y2(k),…,yM(k)]T=A(θ)S(k)+N(k)
(16)
式中:A(θ)=[a(θ1),a(θ2),…a(θK)]為M×K維陣列流形矩陣;S(k)表示入射信號強度;N(k)=[n1(k),n2(k),…,nM(k)]T為陣列高斯白噪聲矢量。
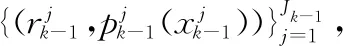
(17)
式中:
(18)
(19)
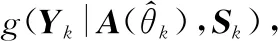
(20)
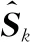
(21)
后向平滑數據為
(22)
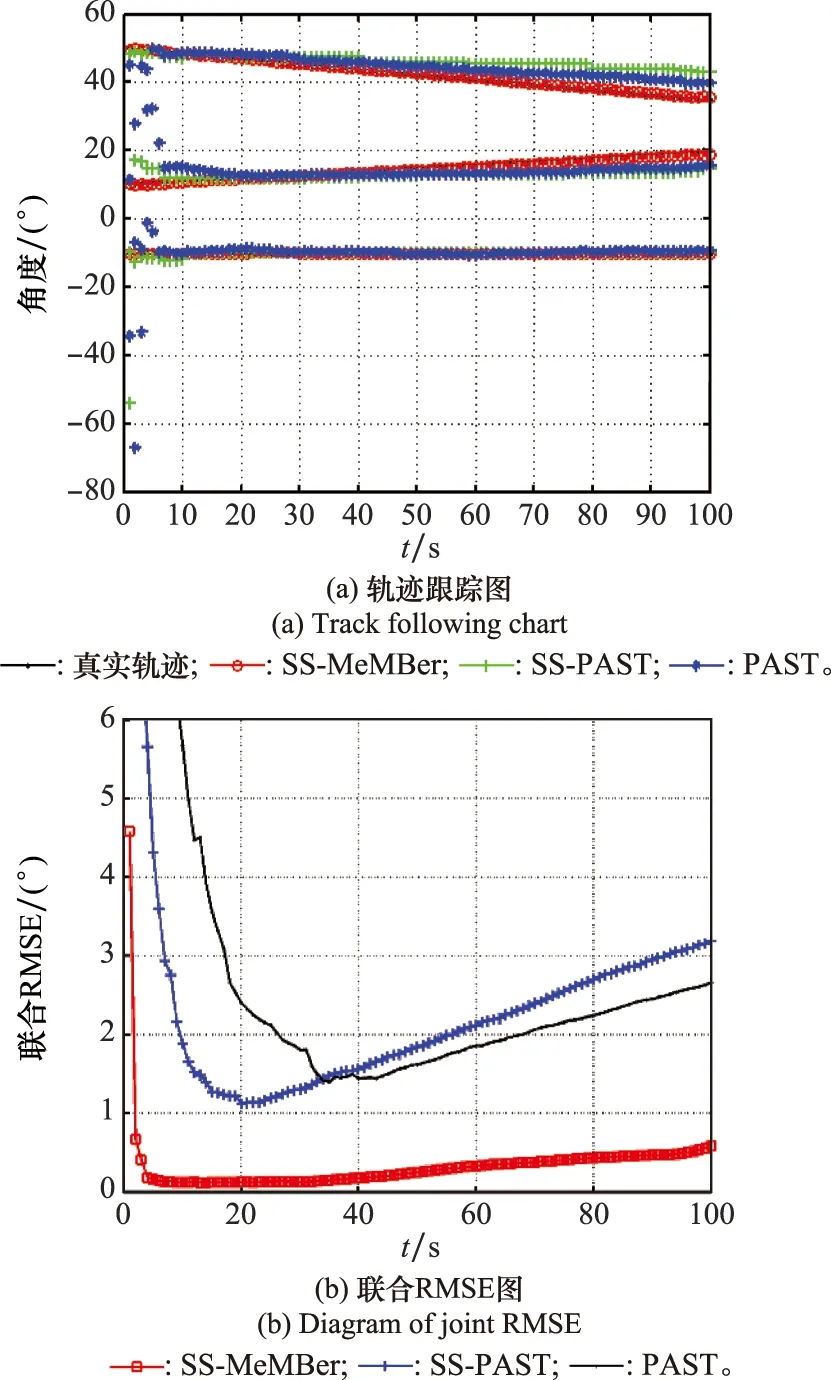
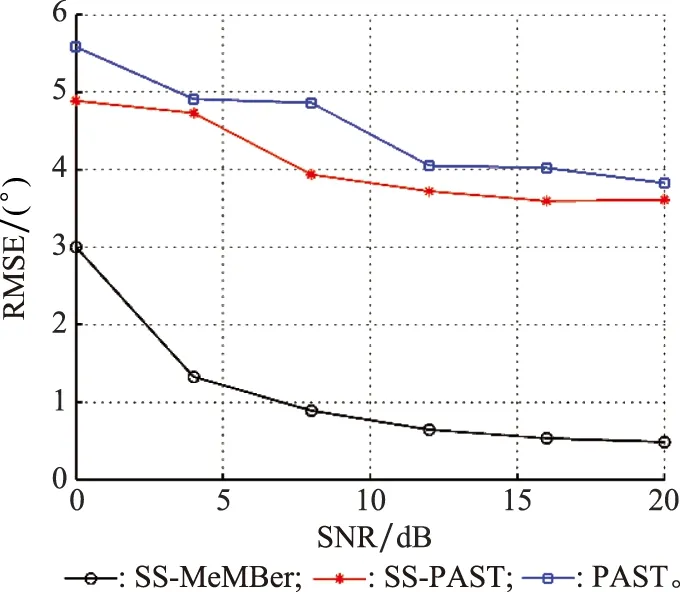
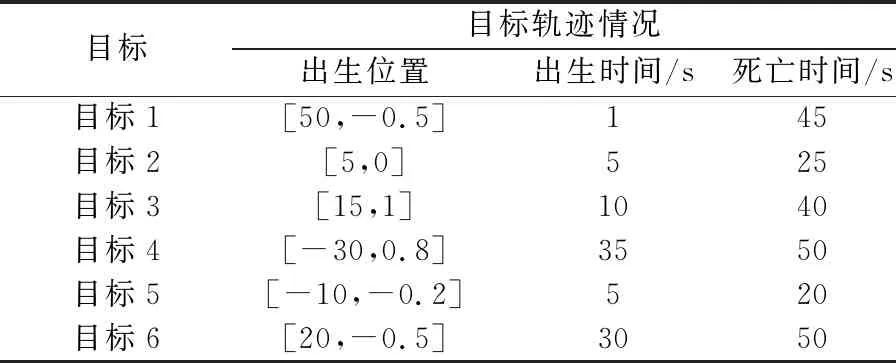
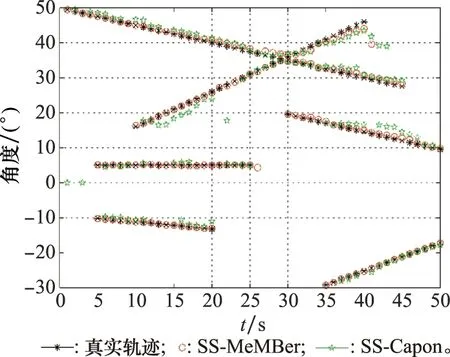
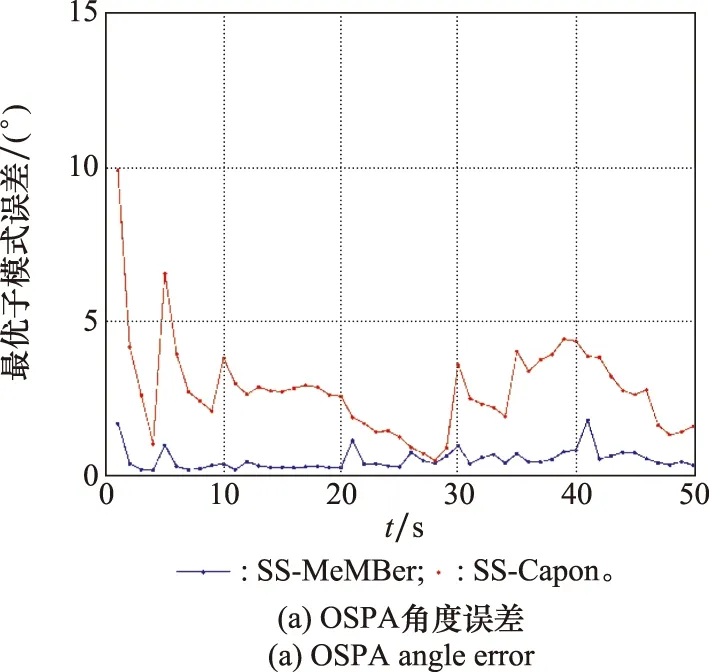
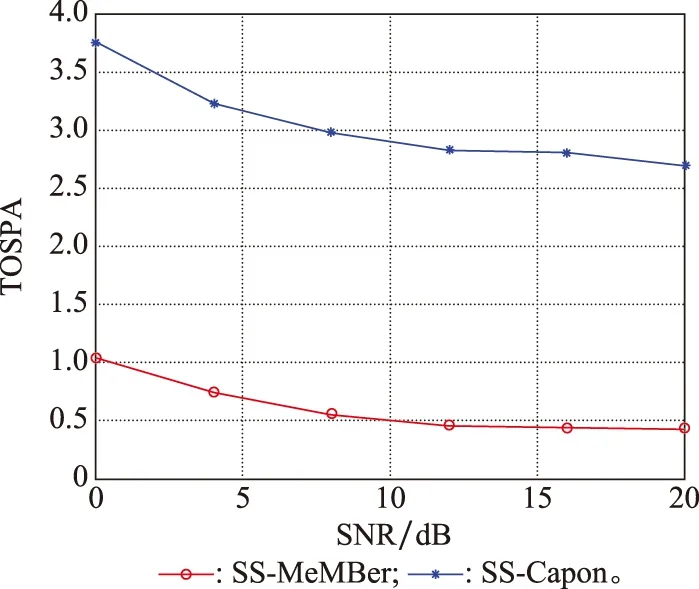
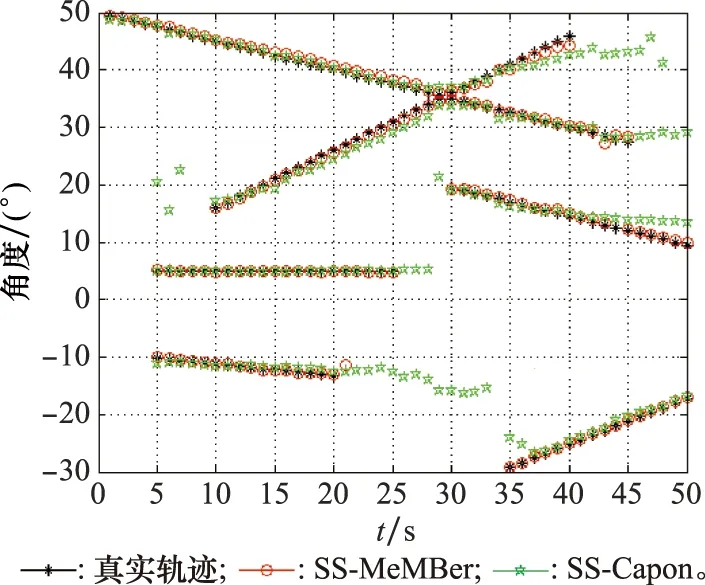
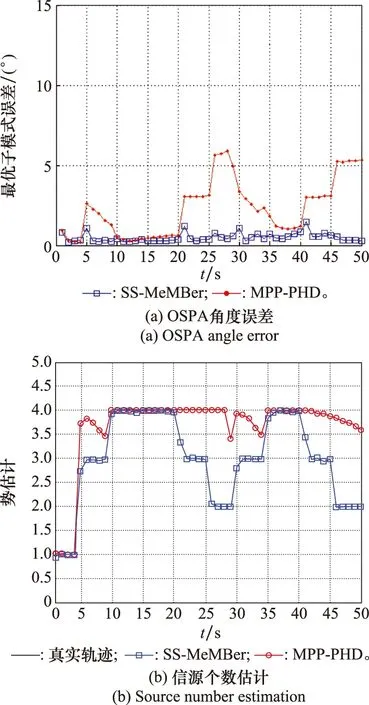
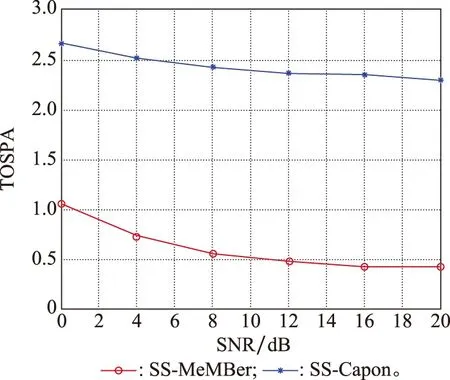
式中:K為信源個數;l是平滑子陣陣元個數,1≤l 則平滑后的數據為 (23) (24) (25) (26) 因此,多伯努利濾波器更新階段參數集分別為 (27) (28) (29) 權重為 (30) 式中:ps表示存活的概率;fk|k-1表示存活粒子的狀態轉移函數;pb表示新生粒子的概率;B表示從建議概率βk中新生的粒子數;與βk相對應的概率密度bk|k-1采用均勻分布模型。 k時刻多目標多伯努利粒子濾波更新階段的后驗概率密度可以表示為 (31) 權重為 (32) 式中:通過所得的噪聲子空間與監測區域任何估計目標的粒子狀態得到MUSIC-偽似然函數為 (33) 多伯努利后驗p(xk|Y1:k)可將式(33)代入式(28)中可得,已知離目標越近的粒子權重就越大,最后通過重采樣選取權重大的粒子,消除權重小的粒子。算法流程如下所示。 下列仿真實驗中,檢驗算法優劣性的指標之一是均方根誤差(root mean square error,RMSE),是指預測值與真實值偏差的平方與觀測次數n比值的平方根,衡量觀測值與真實值的偏差。其定義分別為 (34) (35) 此外,本文還選擇一個度量標準,即最優子模式分配(optimal subpattern assignment,OSPA)誤差[18]。其不僅計算估計角度和真實角度之間的誤差,而且還可以量化當存在的信源被忽略或不存在的信源被錯誤地檢測到時的懲罰,常用來評估多目標濾波問題的性能。OSPA誤差定義為 (36) d(c)(x,y)=min(c,d(x,y)) (37) 式中:d(x,y)=‖x-y‖表示x和y間的距離,x,y分別表示真實值和估計值;集合X={x1,x2,…,xm}和Y={y1,y2,…,yn},m、n分別表示真實值個數和估計值個數;c表示懲罰參數;p表示階數參數;Πn代表從集合{1,2,…,n}中取出m個元素進行排列的集合。 實驗 1條件如下:時間步長ΔT=1 s,陣元個數M=10,信噪比(signal to noise ratio,SNR)為15 dB,觀測時間T=100 s,信源數目為3,狀態時變,數目保持不變,信源初始狀態分別為x1(0)=[50,-0.15]T,x2(0)=[10,0.1]T,x3(0)=[-10,0]T,且接收量測為單快拍量測,信源存活概率為ps,k=0.98;在SS-MeMBer DOA跟蹤算法的預測階段,假設每個時刻有6個新生信源,即JB,k=6,是[-π/2,π/2]上的均勻分布,每一個新生源產生300個粒子,即NB,k=300。 圖1是在SNR為15 dB的條件下,100次MC實驗的軌跡跟蹤效果圖。圖1(a)是軌跡跟蹤圖。圖1(b)是運行100次MC實驗的聯合均方誤差圖。從圖1可以看出跟蹤3個目標時,當目標快速運動時,PAST及基于空間平滑的PAST(spatial smoothing with PAST,SS-PAST)算法由于每次快拍間的步長大,導致子空間跟蹤性能下降。當目標運動緩慢或不變,3個算法跟蹤性能基本一致。因此,本文提出的SS-MeMBer算法在跟蹤快速運動目標時的估計值要比傳統的PAST算法,SS-PAST算法[6]的估計值更接近真實值,RMSE更小。 圖1 DOA跟蹤的軌跡跟蹤和RMSEFig.1 Trajectory tracking and RMSE of DOA tracking 圖2為上述3種算法隨著SNR的變化的聯合RMSE。從圖2可以看出3種算法的聯合RMSE圖都隨SNR增加呈現下降趨勢,SNR越大,RMSE越小。圖2中可以明顯看出,不同SNR下SS-MeMBer算法的RMSE小于SS-PAST算法和PAST算法。 圖2 不同SNR下DOA跟蹤的RMSEFig.2 RMSE of DOA tracking with different SNR 實驗 2由于傳統的DOA跟蹤算法需要預先知道信源個數才能進行DOA跟蹤,不能處理信源數目時變的跟蹤問題。實驗2是考慮信源數目時變,分析SS-MeMBer算法的性能。本文使用平滑后的數據得到的MUSIC空間譜函數作為多伯努利粒子濾波似然函數,提出了SS-MeMBer算法。選擇基于Capon譜函數作為粒子似然函數的多伯努利粒子濾波(簡稱為SS-Capon)算法作為對比算法。其中SS-Capon算法的Capon譜偽似然函數為 (38) 由于Capon波束形成算法的最優性能是建立在采樣快拍數足夠多以及對目標信號導向矢量精確己知的前提之上,當快拍數較少時,Capon波束形成算法會產生高旁瓣的波束響應,從而使得算法性能下降。因此,采用在單快拍空間平滑條件下得到的偽協方差作為平滑后的量測數據進行協方差求逆運算得到Capon譜偽似然函數。 實驗條件如下:陣元個數M=20,SNR為15 dB,觀測時間T=50 s,考慮一個有6個信源的多源檢測場景,其中信源狀態與數目都是時變的,信源的出生死亡時間以及目標運動情況如表1所示。 表1 目標軌跡情況Table 1 Target trajectory condition 圖3是在SNR為15 dB的條件下,6個目標一次MC的軌跡跟蹤圖,從圖3中可以看出本文所提出的SS-MeMBer算法比SS-Capon算法更準確跟蹤目標航跡,SS-MeMBer算法的估計值在真實角度附近波動,且在目標消失情況下能及時檢測到目標消亡。而SS-Capon算法在相同的實驗條件估計角度時出現漏估的情況,并且估計出的角度存在于真實狀態有很大偏差的情況。因此,SS-MeMBer算法比SS-Capon算法跟蹤信源更準確。 圖3 軌跡跟蹤圖Fig.3 Diagram of trajectory tracking 運行100次MC時,為了更好地評估SS-MeMBer算法和MPP-PHD算法性能,選擇OSPA誤差度量,更直觀評估多目標濾波跟蹤問題的性能。圖4是在SNR為15 dB條件下,SS-MeMBer 算法和SS-Capon算法的OSPA誤差圖和勢誤差比較圖。圖4(a)是OSPA角度誤差圖,其中階數參數p=1,懲罰參數c=10°,從圖4(a)中可看出SS-MeMBer算法的OSPA誤差在目標出現的時刻明顯增大,但整體上SS-MeMBer算法OSPA誤差明顯小于SS-Capon算法。圖4(b)是運行100次MC的勢分布估計圖,從圖4(b)中可看出當信源數目時變的時候,SS-MeMBer算法在目標出現或消失時都能夠準確地估計信源數目,其勢估計幾乎能夠與真實的信源個數重合,而SS-Capon算法從勢估計圖上看整體都低估了信源的勢。通過100次實驗結果顯示,SS-MeMBer 算法比SS-Capon算法跟蹤效果更好。 圖4 RMSE和勢估計圖Fig.4 Diagram of RMSE and cardinality estimation 圖5是SS-MeMBer 算法和SS-Capon算法在不同SNR下得到的估計值與真實值之間的TOSPA角度誤差圖,其中TOSPA表示在某一SNR下所有時刻的OSPA時間平均值。從圖5中可以看出,SS-MeMBer 算法和SS-Capon算法在不同SNR的OSPA角度誤差,并且都隨著SNR增大而減小,但SS-MeMBer 算法的OSPA角度誤差都比SS-Capon算法的OSPA角度誤差小。綜上,可以得出在多伯努利濾波器算法實現中采用MUSIC似然函數跟蹤結果比采用Capon譜函數作為似然函數性能更優。 圖5 不同SNR下的TOSPA誤差圖Fig.5 Diagram of TOSPA error with different SNR 本文所提出的SS-MeMBer算法,采用的是多伯努利粒子濾波器估計多目標后驗密度,而PHD濾波是直接估計一階矩來進行跟蹤的,因此選擇了與文獻[14]提出的用于DOA跟蹤的標記點泊松過程PHD(簡稱為MPP-PHD)濾波器作對比。 圖6是在SNR為15 dB條件下,一次MC的軌跡跟蹤圖,從圖6中可以看出,當信源存在時本文所提出的SS-MeMBer算法與MPP-PHD算法都能估計出信源真實航跡,但在信源消失情況下SS-MeMBer算法能及時檢測到目標消亡。而MPP-PHD算法當目標消失時,不能及時估計目標消失,存在一定的延時。 圖6 DOA軌跡跟蹤圖Fig.6 Trajectory of DOA tracking 圖7是在SNR為15 dB,目標數目為6,MC=100時,SS-MeMBer 算法和MPP-PHD算法的OSPA誤差圖和勢誤差比較圖。圖7(a)是OSPA角度誤差圖,其中階數參數p=1,懲罰參數c=10°,從圖7(a)中可看出SS-MeMBer算法的OSPA誤差在目標出現的時刻明顯增大,但整體上SS-MeMBer算法OSPA誤差明顯小于MPP-PHD算法。圖7(b)是運行100次MC的勢分布估計圖,從圖7(b)中可看出當信源數目時變的時候,SS-MeMBer算法估計的勢基本與真實的勢相一致,并且當數目發生變化是也能夠準確的估計信源數目,而MPP-PHD算法對于數目發生變化時不能及時估計時變信源的勢。 圖7 DOA跟蹤RMSE和勢估計圖Fig.7 RMSE of DOA tracking and cardinality estimation 圖8是SS-MeMBer 算法和MPP-PHD算法在不同SNR條件下的估計值與真實值的TOSPA角度誤差圖,從圖8中可以看出SS-MeMBer 算法和MPP-PHD算法的OSPA角度誤差都隨著SNR增大而減小,但整體SS-MeMBer 算法的OSPA角度誤差都比MPP-PHD算法的OSPA角度誤差小。 圖8 不同SNR的DOA跟蹤TOSPA誤差圖Fig.8 TOSPA of DOA tracking with different SNR 本文提出了基于空間平滑的多伯努利濾波器DOA跟蹤算法。該算法直接采用傳感器陣列所得的單快拍數據進入多伯努利濾波中并在更新階段使用空間平滑進行處理,用平滑后的數據構成的矩陣代替協方差矩陣估計陣,生成MUSIC譜函數作為多伯努利的似然函數,并通過SMC方法實現。通過仿真實驗可知當信源數目已知情況下,SS-MeMBer DOA跟蹤算法與SS-PAST及PAST跟蹤算法相比性能更優。信源數目未知情況下也能準確跟蹤數目時變的DOA,與MPP-PHD算法相比,SS-MeMBer算法勢估計更準確,OSPA誤差更小。總體而言,本文所提的基于空間平滑的多伯努利濾波器DOA跟蹤算法,在單快拍量測數據情況下能準確跟蹤時變DOA。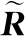
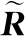
3 SS-MeMBer DOA跟蹤粒子濾波實現算法

4 仿真實驗
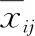
4.1 信源數目固定不變的DOA跟蹤
4.2 信源數目時變的DOA跟蹤
5 結 論

