基于連續信任函數理論的魯棒雷達目標檢測方法

楊 威,劉永祥,付耀文,黎 湘

(國防科技大學電子科學學院,湖南 長沙 410073)

0 引 言

目標檢測是雷達的基本功能,不僅影響雷達的探測性能,也深刻影響著后續雷達目標跟蹤與識別等任務,其魯棒性決定了雷達應用的成敗。雷達目標檢測就是在含有噪聲的雷達回波中,完成對“目標存在與否”假設的檢驗判斷。鑒于噪聲的隨機特性以及雷達目標回波幅度隨著姿態、頻率、極化等多因素影響,雷達目標檢測常在貝葉斯理論框架下建模為NP(Neyman-Pearson)問題[1],即將虛警概率限定在一個有限的水平,使檢測概率最大化。通過相干或非相干積累，可以進一步提升雷達目標檢測性能[2-5]。

實際應用及理論研究中,大多假設雷達目標由多個獨立散射體構成,每個散射體的雷達散射截面積(radar cross section,RCS)獨立且不變,但位置隨機。根據電磁散射理論和中心極限定理,此類目標經線性檢波器輸出的雷達目標回波幅度服從瑞利分布[6]。對于目標的回波幅度，也有部分學者建模時采用高斯混合分布[7-9]、瑞利混合概率密度函數[10-11]、多自由度卡方概率密度函數[6]、混合伽馬分布[12]、混合Gp分布[13-15]。在貝葉斯理論框架下,NP檢測的最終依據就是當線性檢波器輸出電壓大于等于某門限,則判定有目標；當輸出電壓小于某門限,則判定無目標[16-18]。其中,門限值由目標的平均幅度、噪聲功率和虛警概率3個參數決定。一方面,針對上述NP檢測原理,在雷達對抗領域提出了不少欺騙式干擾策略,即提高干擾源的功率、漸進地誘騙跟蹤鎖定波束,從而實現戰術逃逸[19-21]。另一方面,由于目標回波起伏特性,極可能導致檢測方法作出過于自信的決策,從而存在信息損失,如當輸入待檢測回波幅度觀測值很大時,既有可能是目標回波幅度起伏特性導致,也有可能是由外來干擾產生,這種信息在NP準則下是無法進行合理表征的。因此,上述NP方法缺乏檢測魯棒性,在有電子干擾的場景中,其恒虛警特性將受到破壞。對于外來干擾,既可以是先驗假設目標之外的外來實體目標,也可以是先驗假設目標之外的欺騙式干擾目標,反映此類目標回波幅度特性的平均RCS大于先驗假設目標的平均RCS。同時,外來干擾也可以是先驗假設噪聲之外的噪聲,反映此類噪聲回波幅度特性的平均RCS小于先驗假設噪聲的平均RCS,其中先驗假設噪聲也即建模噪聲,可稱為模型噪聲。

針對該問題,本文利用連續信任函數理論[22-24]在不確定性信息表征方面的優勢,嚴格推導了一種魯棒檢測器,使其同時對模型噪聲和外來干擾都具備一定的判斷力,體現在可以提供更豐富更準確的決策量化信任度。針對該檢測器不存在解析解的難題,提出了一種通過查表進行數值擬合近似的策略。實驗結果驗證了本文方法的魯棒性。

1 連續信任函數理論基礎

假設一個離散的辨別框架Θ={θ1,θ2,…,θC},其中θc表示第c類假設,C表示總假設數目。經典的貝葉斯理論是將所有的信任(即可能性)分配給上述辨別框架的每一個假設,稱之為各假設成立的概率。而在信任函數理論[25]框架中,其信任是分配給辨別框架的任意子集S?Θ,如下所示:

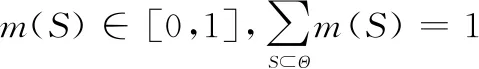
(1)

式中:m(·)為基本信任分配(basic belief assignment,BBA)函數。

空集?上所獲得的基本信任質量m(?)表示外來干擾的可能性,而全集Θ上所獲得的基本信任質量m(Θ)表示完全無知的可能性大小。通常,任意子集S?Θ所獲得的基本信任質量m(S)>0表示假設來自于該子集的可能性,但無法判定該子集中到底哪個假設成立,S稱之為焦元。當所有焦元滿足嵌套關系時,該基本信任分配函數被稱為一致基本信任分配函數。

基于m(·)函數,可以推導得到信任函數bel(·)和似然函數pl(·),三者間滿足一一映射關系：

(2)

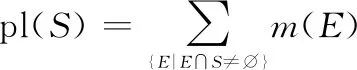
(3)

式中：任意集合?Θ。

在最終輸出硬判決時,基于最小投注原理,可以將m(·)函數轉換為投注概率函數BetP(·)：

(4)

判決具有最大投注概率的假設成立,其中|S|表示集合S的勢,即其元素數目。

這些函數是定義在離散辨別框架Θ內的,但是大部分實際觀測空間為連續實數域R。在連續實數域中,基本信任分配函數可擴展為基本信任密度(basic belief density,BBD)函數,假設實數域中所有連續閉區間集合F={[a,b]|a≤b},則BBD函數定義為fF:F→[0,+∞],即mF([a,b])=fF(a,b)。在連續實數域內,相關的信任函數、似然函數與投注概率函數的定義如下所示:

(5)

(6)

(7)

在連續信任函數理論框架內,假設知識由條件投注概率密度函數BetfR[θc](·)表示,其中?θc∈Θ。文獻[25]已經證明,在最小投注概率準則條件下,當條件投注概率密度函數滿足單峰特性時,由其可推導得到一個唯一的一致基本信任分配函數,其對應的似然函數見定理1所示。

定理1假設BetfR[θc](·)函數的峰值所處位置為μ∈R,且X=[x,y],當x>μ時,似然函數如下所示：

(8)

式中:γ(t)<μ且BetfR[θc](γ(t))=BetfR[θc](t),γ(t)也被稱為t的等投注概率投影。

為論述方便,令t=γ-1(t)。事實上,對于一個單峰條件投注概率密度函數BetfR[θc](·),假設其對應的一致基本信任分配函數為mR[θc](·),則任意實數域上的點觀測z∈R,當z=min(z∈X)且min(z∈X)>μ時,或者當z=max(z∈X)且max(z∈X)<μ時,則滿足plR[θc](z)=plF[θc](X)。因此,在最小投注概率準則條件下,當獲得的點觀測z∈R且z≥μ時,其條件觀測似然函數為

(9)

當z<μ時,其條件觀測似然函數為

(10)

由廣義貝葉斯定理(general bayes theorem,GBT),當所有的條件似然函數已知時,其在離散辨別框架Θ上基本信任分配函數為

(11)

實際應用中,不可能獲得嚴格意義上的條件投注概率密度函數BetfR[θc](·),常取為條件概率密度分布函數,即令BetfR[θc](·)=pθc(·)[5]。文獻[26-27]對于高斯分布、α-穩態分布等典型的單峰條件投注概率密度函數給出了對應的條件似然函數plR[θc](·)計算公式。但是,在雷達目標檢測領域,目標回波幅度隨著觀測視角、探測頻率、極化方式等多因素影響,其起伏模型往往被建模為瑞利概率密度函數：

(12)

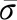
2 問題描述與魯棒雷達目標檢測

2.1 問題描述

假設雷達回波幅度觀測值為z∈R+,表示檢波器輸出的電壓絕對值,其模型噪聲條件觀測似然函數值為noise(z)=和真實目標條件觀測似然函數值為當兩者都極小時或當兩者比值接近于1時,外來干擾的可能性或模型噪聲與真實目標間的不可區分度都急速上升,給目標檢測決策帶來了巨大風險。但按照NP準則,當模型噪聲幅度的條件概率密度函數和真實目標幅度的條件概率密度函數已知時,給定一個固定的虛警概率,判斷觀測z是否大于某一個門限,當大于該門限時判斷為真實目標,當小于該門限時判斷為模型噪聲,這種檢測方法無法區分外來干擾,在高度不確定的條件下也會給出一個明確結論,缺乏魯棒性。引起該問題的核心原因在于貝葉斯理論中將所有信任質量賦予辨別框架Θ={θ0,θ1}中的單一元素子集,其中θ0表示模型噪聲假設,θ1表示真實目標假設。

如前所述,連續信任函數理論框架可以更好地表征不確定信息。針對目標檢測問題,可以將基本信任質量賦予空集表示外來干擾的可能性大小,賦予全集表示真實目標和模型噪聲完全無法區分的可能性大小。然而,有效運用連續信任函數理論,必須解決由非對稱的單峰條件投注概率密度函數計算如式(8)～式(10)所示的條件觀測似然值,最后再利用GBT在離散辨別框架上完成信任函數構造,基于此完成目標檢測的軟判決。

2.2 瑞利密度函數的條件觀測似然值計算策略

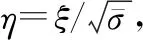
prls(η)=2ηexp(-η2)

(13)

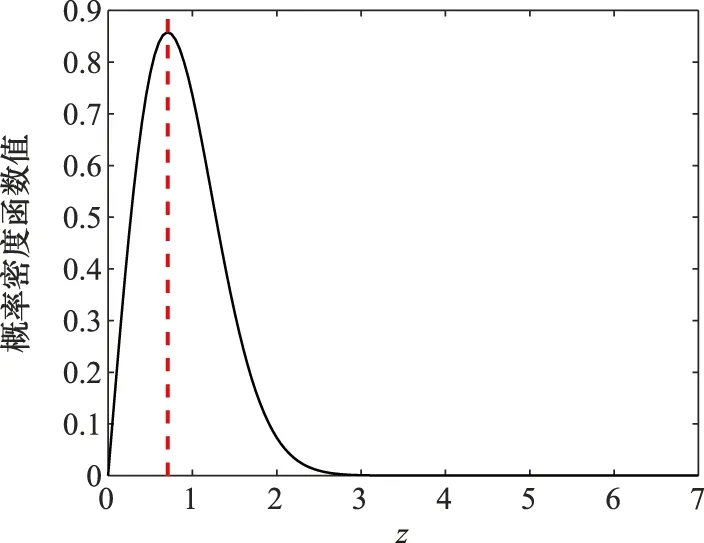
圖1 標準瑞利概率密度函數曲線Fig.1 Standard Rayleigh probability density function curve

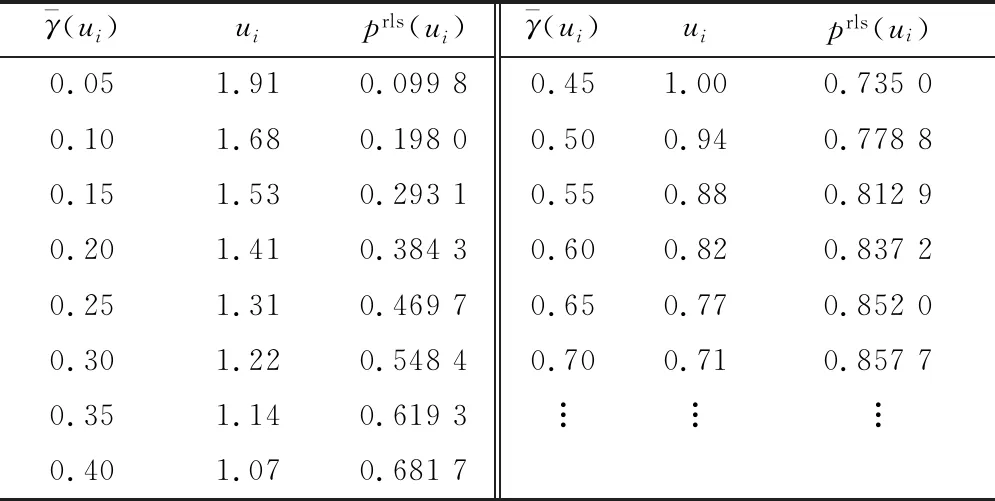
表1 標準瑞利概率密度函數的近似等投注概率對Table 1 Approximate Iso-pignistic points for standard Rayleigh probability density function

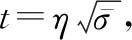
(14)

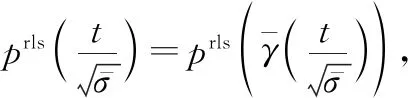
(15)

由式(15)可以得到等投注概率對變換公式：

(16)

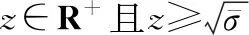
(17)

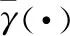
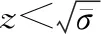
(18)

因此,根據如式(13)和表1所示的標準瑞利概率密度函數的等投注概率表,查詢獲得t的近似值為

(19)

由此獲得近似求和的下限為

(20)

則可完成條件觀測似然函數計算。

2.3 基于信任函數理論的魯棒雷達目標檢測算法

依據第2.1節和第2.2節所述,具體算法的偽代碼如表2所示,圖2給出了該檢測方法的結構示意圖。

表2 基于信任函數理論的魯棒雷達目標檢測算法Table 2 Robust radar target detection algorithm based on trust function theory

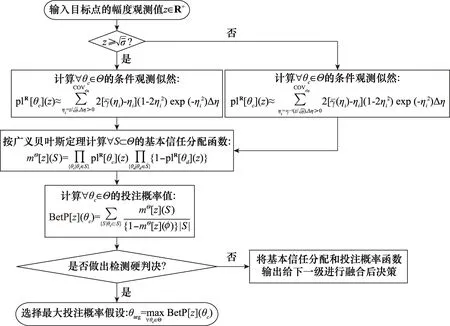
圖2 基于連續信任函數理論的魯棒雷達目標檢測器結構Fig.2 Configuration of the robust radar detector based on the continuous belief function theory

3 數值實驗分析

基于本文所提如表2所示的步驟1和步驟2,則可以畫出任意點觀測z∈(0,+∞)對應的條件觀測似然函數plR[θn](·)和plR[θt](·)的分布曲線,如圖3所示，其中橫坐標表示檢波器輸出的絕對值電壓，單位為伏特；縱坐標表示輸出電壓的概率密度函數值及其對應觀測似然函數值的大小，無量綱。由圖3可以看出,信任函數理論框架下的條件觀測似然函數plR[θn](z)或plR[θt](z)并不等于貝葉斯理論框架下的條件概率密度函數,但根據定理1的假設可以知道,前者是由后者推導得來。

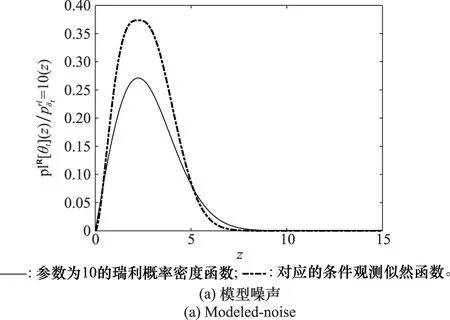
圖3 雷達模型噪聲和真實目標回波幅度起伏概率密度函數和對應條件觀測似然函數曲線Fig.3 Amplitude fluctuation probability density function for modeled-noise and true target and their corresponding conditional plausibility functions

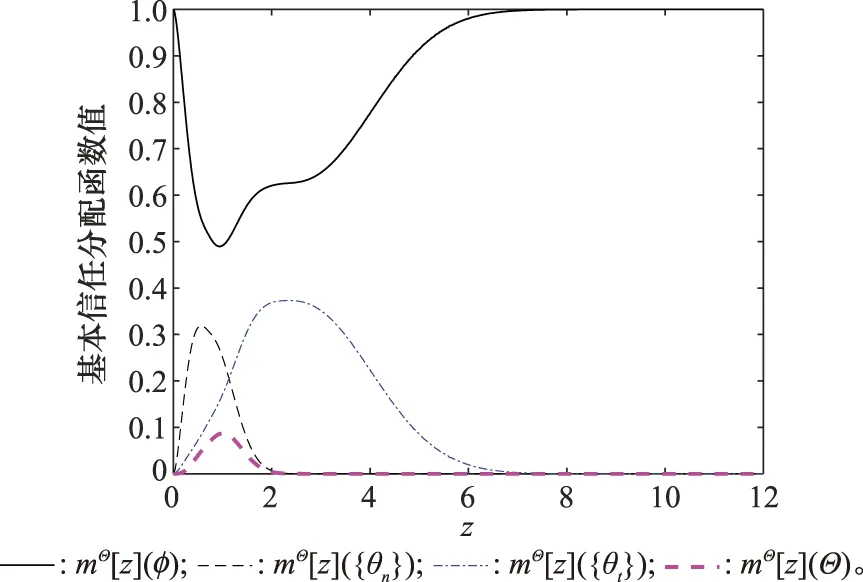
圖4 條件化的基本信任分配函數Fig.4 Conditional basic belief assignment function

進一步按照表2所示的步驟3,可以畫出這些點觀測所對應的條件基本信任分配函數mΘ[z](·),如圖4所示。其中，橫坐標表示檢波器輸出的絕對值電壓，單位為伏特；縱坐標表示輸出電壓的基本信任分配函數值的大小，無量綱。由圖4可以看出,當點觀測極小或者極大時,賦予空集的基本信任質量都趨近于1,即由于模型噪聲和真實目標的條件觀測似然都很小,意味著此模型噪聲和真實目標都不存在的可能性或外來干擾的可能性急速上升。當點觀測在模型噪聲條件幅度起伏概率密度函數BetfR[θn](·)峰值位置附近時,賦予模型噪聲假設的基本信任質量相對最大；當點觀測在真實目標條件幅度起伏概率密度函數BetfR[θt](·)峰值位置附近時,賦予真實目標假設的基本信任質量相對最大；當點觀測在前述兩個峰值之間時,模型噪聲與真實目標間的不可區分度又增加,因此賦予全集的基本信任質量達到最大值。由此可以看出,基于連續信任函數理論的雷達目標檢測器具有更強大的信息表征能力。

最后按照表2所示的步驟4,可以計算出其對應的條件投注概率值BetP[z](·),如圖5所示。其中，橫坐標表示檢波器輸出的絕對值電壓，單位為伏特；縱坐標表示輸出電壓的條件概率值的大小，無量綱。在貝葉斯理論框架下,由于模型噪聲和真實目標的先驗概率未知,因此不同假設的概率P(·|z)與其條件概率密度函數f(·|θn)=BetfR[θn](·)或f(·|θt)=BetfR[θt](·)成正比。實際應用過程中,NP準則按照基于對虛警概率和檢測概率兩個指標的需求,合理設定一個門限值Th,當輸入點觀測z≥Th時,則認定為目標,否則認定為模型噪聲。事實上,在現代電子干擾的背景下,采用距離、速度、角度、聯合多維度欺騙等對抗措施時,干擾假目標信號的幅度往往大于真實目標的幅度觀測,因此在NP準則下很容易被誘騙,其恒虛警(constant false alarm ratio,CFAR)特性也將遭到破壞,缺乏魯棒性。由圖5曲線可以看出,連續信任函數理論框架下得到的投注概率與貝葉斯理論框架下得到的后驗概率結果還是有區別的。與貝葉斯理論相比,連續信任函數理論不需要對未知的先驗概率進行先驗配置,而且圖4表明后者具有更豐富的信息表征能力,可以高效表征模型噪聲、真實目標與外來干擾的檢測不確定性,因此具有更高的魯棒性。

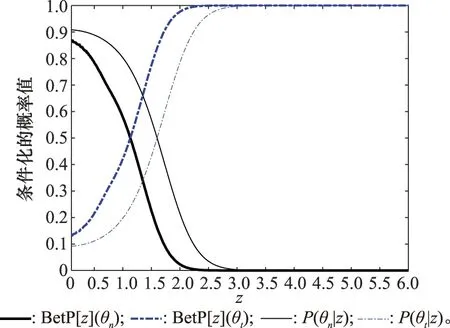
圖5 條件投注概率及貝葉斯后驗概率Fig.5 Conditional bet probability and Bayesian posterior probability

4 結 論

本文針對雷達目標檢測問題,在連續信任函數理論框架下,提出了一種魯棒檢測器。相比貝葉斯理論框架中的NP準則,新檢測器可以更好地區分模型噪聲、真實目標、外來干擾等,具有更豐富的信息表征能力。在計算時,該檢測器需要求得瑞利概率密度函數的等投注概率投影點,針對其不存在解析解的難題,設計提出了一種數值近似的解算方法。理論分析結果驗證了該檢測器的魯棒性。相關檢測軟決策信息還可以輸入后端數據處理模塊,如特征輔助的多目標跟蹤等。

目前,正在向更廣泛的噪聲和目標幅度起伏模型推廣,包括但不限于高斯混合分布、瑞利混合概率密度函數、多自由度卡方概率密度函數、混合伽馬分布、混合Gp分布等；另一方面,未來將利用更多的實測數據,對本文所提檢測算法的接收機工作特性曲線進行測試驗證,在難以推導得到接收機工作特性特性的解析解時,可通過蒙特卡羅仿真實驗方式獲取；最后,利用信任函數理論中的融合規則,研究該檢測器的積累檢測性能也是值得探索的一大方向。