導航接收機帶外電磁干擾的效應規(guī)律及預測方法研究

張慶龍,王玉明,程二威,陳亞洲,馬立云

(陸軍工程大學石家莊校區(qū)電磁環(huán)境效應國防重點實驗室,河北 石家莊 050003)

0 引 言

隨著我國北斗系統(tǒng)的日益完善,針對北斗導航接收機在復雜電磁環(huán)境下的可用性和完好性研究逐漸成為國內外的研究熱點。尤其是在戰(zhàn)時,各種用頻裝備的不斷投入應用,使得戰(zhàn)場上的電磁環(huán)境日益復雜,對無人裝備導航、導彈的精確制導等構成了嚴重的影響。目前，大部分研究主要是理論上分析了不同電磁干擾對導航接收機跟蹤環(huán)路的影響[1-6],以及如何提高其抗干擾能力[7-9],為導航接收機的前期設計提供了理論依據和技術支持。但由于在實際的工程應用中,各種復雜電磁干擾信號作用于接收機時,僅僅考慮電磁干擾對跟蹤環(huán)路的影響是遠遠不夠的,電磁干擾下接收機的射頻前端會產生各種非線性效應,同樣會影響接收機的跟蹤性能。

現(xiàn)有標準中規(guī)定的電磁敏感度試驗都是基于單源輻射條件下開展的,試驗得到的干擾閾值不能代表授試設備在戰(zhàn)場復雜電磁環(huán)境中的生存能力[10],所以多源電磁干擾下導航接收機的效應研究極為迫切,然而國內外在這方面的研究極少。文獻[11]通過仿真手段研究了存在多個干擾時,導航接收機的失鎖效應規(guī)律,但并沒有作出具體深入的分析,并且仿真實驗只是針對跟蹤環(huán)路進行了建模,沒有考慮射頻前端的實際狀態(tài),不能全面代表接收機整機在復雜電磁環(huán)境中的真實情況。

文獻[12]以導航接收機的工作機理出發(fā),建立了導航接收機帶內雙頻干擾的模型,并通過試驗驗證了該模型的可靠性。但在實際的戰(zhàn)場電磁環(huán)境中,由于各種用頻裝備的使用,以及針對性的電子對抗干擾,使得導航接收機同樣面臨各種各樣的帶外大信號干擾。文獻[13-16]均指出帶外干擾同樣會對導航接收機性能造成不利影響。文獻[17]針對帶外干擾對導航接收機射頻前端的影響進行了概述性分析,但并沒有進行深層次理論分析。因此，有必要從理論上研究帶外干擾對導航接收機的影響,并建立導航接收機的帶外干擾預測模型,用于無人裝備導航接收機的帶外干擾效應預測,為無人裝備在面臨復雜電磁環(huán)境時,及時規(guī)避風險和重新規(guī)劃飛行軌跡提供依據,提高無人裝備任務的成功率,同時又可以為導航接收機的進一步加固防護提供依據。

1 導航接收機帶外雙頻干擾預測模型

對于導航接收機而言,當干擾信號為帶內干擾時,較低的干擾信號功率就能引起接收機內部通道的衛(wèi)星跟蹤丟失,此時接收機射頻前端的非線性并不突出。但是當較強的帶外干擾信號作用于接收機的射頻前端時,會使得接收機內部的線性器件可能工作于截止、飽和甚至擊穿的工作狀態(tài),進而導致射頻前端的內部噪聲增大,降低了接收機內部的信噪比,嚴重時會導致接收機在相關處理時無法解調出衛(wèi)星信號,造成大信號阻塞現(xiàn)象。此時,可以按照矢量法來分析其阻塞效應機理[18]。

導航接收機天線接收到信號r(t)[19]可以表示為

r(t)=s(t)+n(t)+J(t)

(1)

式中:s(t)為天線接收的導航信號功率;J(t)為干擾信號功率;n(t)為天線接收的窄帶噪聲功率,其帶寬與射頻前端最窄的一級濾波器相對應,因為這一部分噪聲才是最終進入到接收機相關處理過程中的噪聲,因此式(1)可寫為

r(t)=s(t)+g(t)

(2)

式中:g(t)=J(t)+n(t)≈J(t)。由于噪聲信號的功率遠低于帶外干擾信號功率,信號g(t)的特征主要取決于帶外干擾信號J(t),為了便于利用矢量法進行公式推導,在此處對噪聲進行忽略,但后續(xù)過程中不能對噪聲進行忽略。

(3)

式中:Ps為導航信號功率；PJ為干擾信號功率；fs為導航信號頻率；fJ為干擾信號頻率；Us為導航信號幅度；UJ為干擾信號的幅度。考慮到射頻前端有多級濾波器的因素,實際到達敏感非線性器件時的信號可表示為

r(t)=AsUscos(2πfst)+AJUJcos(2πfst)

(4)

式中:As和AJ為濾波器對導航信號和干擾信號的選頻系數。當帶外大信號進入接收機射頻前端時,AsUs/AJUJ=α?1,信號頻率之間的關系如下所示:

(5)

式中:fd為干擾信號和有用信號頻率之差。

假設fs=fJ+fd,干擾信號和導航信號的合成信號矢量圖如圖1所示,合成信號r1(t)可以進一步表示為

r1(t)=R1(t)cos(2πfJt+θ)=

R1(t)cos[2π(fs-fd)t+θ]

(6)

式中:

(7)

(8)

圖1 一個干擾信號下的矢量圖Fig.1 Vector illustration under an interference signal

設限幅電壓為UX,限幅器之前的信號增益為K0。當AsUs+AJUJUX時,輸出信號幅值為UX,輸出信號如下所示:

r1(t)′=UXcos[2πfJt+αsin(2πfdt)]=

UX[cos(2πfJt)cos(αsin 2πfdt)-

sin(2πfJt)sin(αsin 2πfdt)]

(9)

根據貝塞爾函數理論,具有如下展開式:

(10)

式中:Jn(α)為第一類n階貝塞爾函數[19],J0(α)≈1,J1(α)≈0.5α。結合式(10),對式(9)中的第二項進行展開,并且只考慮基波分量,如下所示:

-UXsin(2πfJt)sin[αsin(2πfdt)]≈

-UXsin(2πfJt)·2J1(α)sin(2πfdt)=

(11)

有用信號的分量為式(11)中的第一項,則有用信號增益為

(12)

根據式(12)可以看出,有用信號的增益與限幅幅值Ux和干擾信號幅值UJ有關。當導航接收機同時面臨兩個帶外干擾信號時,此時天線接收到的信號為

r(t)=s(t)+n(t)+J1(t)+J2(t)≈

s(t)+J1(t)+J2(t)

(13)

首先,利用矢量的方法分析兩個干擾信號的和信號,此處不考慮噪聲信號的影響,如圖2所示。

圖2 兩個干擾信號下的矢量圖Fig.2 Vector illustration under two interference signals

根據圖2可以計算出干擾信號的合成幅值SJ(t)和相位φ,如下所示:

(14)

式中:fa=fJ2-fJ1。進一步將干擾信號與有用信號進行合成,最終的合成信號為的r2(t)。

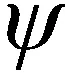
(15)

式中:

(16)

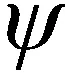
(17)

式中:fb=fs-φ。同樣,當疊加信號的幅值大于限幅幅值UX時,輸出信號為

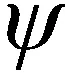
(18)

只考慮有用信號的增益,對式(18)中第二項依據貝塞爾理論進行展開,得到

(19)

有用信號增益為

(20)

假設這兩個帶外干擾信號同時作用時,造成接收機衛(wèi)星跟蹤丟失時的干擾幅值為UJ1和UJ2,而二者單獨作用時,造成接收機衛(wèi)星跟蹤丟失時的干擾幅值為U1和U2,結合式(12)和式(20)可以得出:

(21)

進一步對式(21)進行化簡,并根據帕斯瓦爾恒等式,正弦連續(xù)波的平均功率為P=U2/2R,整理可得

(22)

式中:P1和P2分別為單頻電磁干擾下,不同頻率對應的敏感閾值;Rf為衛(wèi)星跟蹤丟失時的干擾效應壓制系數,具體表示為:當Rf<1時,表示當前雙頻帶外干擾信號功率的組合仍在安全閾值內,不會影響接收機內部對某一衛(wèi)星信號的穩(wěn)定跟蹤；當Rf≥1時,表示當前雙頻干擾信號功率的組合導致接收機大概率不能穩(wěn)定跟蹤某一衛(wèi)星信號。

2 導航接收機帶外雙頻干擾效應試驗

2.1 導航接收機單頻連續(xù)波干擾效應試驗

為了驗證第1節(jié)所建模型的正確性,本節(jié)以某型北斗導航接收機為試驗對象,接收信號為北斗B1I信號。綜合考慮試驗成本以及實驗室現(xiàn)有的條件,實驗方案采取模擬源與干擾信號有線測試的方法[20],試驗配置圖如圖3所示。上位機控制導航信號模擬器產生特定功率的衛(wèi)星導航信號;單頻信號源產生干擾信號,與導航信號經定向耦合器一同注入到導航接收機射頻前端模塊,然后再同時送入導航接收機內部,其中定向耦合器模塊可以避免信號反射對導航信號模擬器或信號產生影響。導航接收機通過232數據線與上位機連接,用于監(jiān)測并顯示當前接收機的各種狀態(tài)參數。

圖3 單源電磁干擾效應試驗Fig.3 Single-source electromagnetic interference effect experiment

試驗過程中選擇3顆北斗衛(wèi)星進行觀察,接收機接收衛(wèi)星信號初始載噪比為40 dB ·Hz,以接收機內部載噪比跟蹤門限值為失鎖判據[21],得到3號星、8號星和12號星的敏感閾值曲線。其中，敏感閾值是指在某一干擾信號頻率下衛(wèi)星跟蹤丟失時干擾信號的功率,如圖4所示。

圖4 不同衛(wèi)星的敏感閾值曲線Fig.4 Sensitivity threshold curves of different satellites

根據圖4可以得出以下結論:

結論 1B1I信號導航接收機的最低敏感閾值出現(xiàn)在1 561.098±2.046 MHz頻段內。不同衛(wèi)星的最低敏感閾值和敏感頻率不同,這與導航衛(wèi)星測距碼的線譜有關[22]。

結論 2在主敏感頻帶外還存在一些其他敏感頻帶,這些敏感頻帶閾值比主敏感頻帶至少高出50 dB。在主敏感頻帶左側(干擾信號頻率小于1 561 MHz一側),存在三級敏感頻帶,且隨著干擾信號頻率遠離導航信號頻率,每一級敏感頻帶的敏感閾值逐漸上升。

結論 3在主敏感頻帶右側(干擾信號頻率大于1 561 MHz一側),存在兩級敏感頻帶分別約為1 571～1 576 MHz和1 591～1 596 MHz。

出現(xiàn)結論2和結論3中所述敏感頻帶是由于接收機內部混頻以及晶振空間輻射的影響[23-25],該接收機的本振頻率fL為1 577 MHz,中頻信號帶寬約為13.9～18.9 MHz(中頻信號帶寬受中頻濾波器影響,一般略大于導航信號帶寬),晶振頻率fO為10 MHz。當干擾信號頻率為1 591～1 596 MHz時,會有干擾信號通過混頻下變頻成為接收機中頻信號頻率,進而對后續(xù)的相關處理形成中頻干擾。而形成結論2中其他敏感頻帶的原因是因為接收機的混頻和晶振空間輻射的影響,混頻器存在這一特性[26-27]:混頻器的輸出信號除了期望的中頻信號外,還包含有輸入信號的頻率成分。以1 548～1 553 MHz敏感頻段為例,設fB為該頻段內某一干擾信號的頻率,則有：

f=fL-nfO-fB

(24)

式中:n=1,2,…。

按式(24)的混頻方式會有中頻信號頻段的頻率輸出。當取n=1時,混頻器輸出的信號頻率分量中包含有中頻信號的成分。同理，當n取2或3時,分別對應主敏感頻帶左側的二級和三級敏感頻帶。式(24)中右側的第一級敏感頻帶的成因也是由于混頻器和晶振空間輻射造成的。

此外,通過圖4中不同衛(wèi)星的敏感曲線可以發(fā)現(xiàn),除敏感頻帶外,不同衛(wèi)星敏感閾值基本相同。結合以上有關混頻器的分析,說明當干擾信號頻率位于這些頻點時,并沒有干擾信號混入中頻。造成接收機內部衛(wèi)星跟蹤丟失的主要原因為射頻前端的阻塞,導致導航信號經模數轉換器 (analog to digital converter,ADC)量化[28-29]后,功率不再滿足接收機的跟蹤靈敏度,從而導致衛(wèi)星跟蹤丟失。

2.2 導航接收機帶外雙源干擾試驗

帶外雙源干擾試驗在單源干擾試驗的基礎上增加了一套矢量信號源,干擾信號和導航信號同樣通過定向耦合器一起注入到導航接收機內部,如圖5所示。

圖5 雙源電磁干擾效應試驗Fig.5 Dual-source electromagnetic interference effect experiment

試驗過程中共選取了3組干擾信號頻率,第1組為f1=1 596 MHz和f2=1 610 MHz,第2組為f3=1 520 MHz和f4=1 600 MHz,第3組為f5=1 510 MHz和f6=1 500±1 MHz;試驗觀察的衛(wèi)星為8號星。為了減少試驗過程中由于信號源和接收機的穩(wěn)定性所引入的誤差,每組試驗數據的記錄為3次測試結果的平均值。試驗數據以及預測模型驗證結果如表1～表3所示。

表1 第1組雙頻干擾試驗數據Table 1 The first set of dual-frequency interference experiment data

表2 第2組雙頻干擾試驗數據Table 2 The second set of dual-frequency interference experiment data

表3 第3組雙頻干擾試驗數據Table 3 The third set of dual-frequency interference experiment data

根據表1～表3的的試驗結果,可以得出以下結論。

(1)根據模型計算的Rf值基本在1左右,相對誤差在±2 dB以內,證明該模型在預測導航接收機在雙頻干擾下衛(wèi)星跟蹤丟失是有效的。

(2)當接收機內衛(wèi)星跟蹤丟失時,雙頻干擾信號的功率存在負相關的關系,即一個信號的功率增大,另一個信號的功率減小。

(3)對比3組試驗數據的誤差結果,可以看出當雙頻干擾信號的頻率差較大時,預測誤差相對較大,但依舊滿足國軍標規(guī)定的3 dB允差[30]。誤差相對較大的原因是由于在預測模型公式推導階段,為了簡化推導過程做了一些近似處理,而雙頻干擾的頻率差就是近似處理的一部分,所以頻率差會影響最終的模型誤差。

3 結 論

本文以某型北斗導航接收機為研究對象,開展了單頻和雙頻帶外干擾的注入效應試驗,并根據試驗數據驗證了雙頻帶外干擾預測模型的有效性。主要結論如下:

(1)本文基于射頻前端阻塞的機理,推導得出了帶外雙頻干擾對導航接收機衛(wèi)星跟蹤丟失的預測模型;

(2)通過單頻連續(xù)波注入效應試驗,得到了導航接收機的敏感閾值曲線,并對主敏感頻帶外其他敏感頻帶的形成機理進行了分析,得知混頻器和晶振空間輻射是造成這些敏感頻帶的主要原因;

(3)通過開展雙頻干擾注入效應試驗,驗證了預測模型的預測誤差基本在±2 dB以內,該預測模型可作為判斷導航接收機受到帶外雙頻干擾后是否出現(xiàn)了衛(wèi)星跟蹤丟失現(xiàn)象的依據。