基于關聯計算的相控陣雷達前視成像技術

阮 鋒,郭 亮,李亞超,許 然

(1.西安電子科技大學物理與光電工程學院,陜西 西安 710071;2.西安電子科技大學電子工程學院,陜西 西安 710071;3.北京電子工程總體研究所,北京 100076)

0 引 言

在不遠的將來,空戰面臨的作戰環境會越來越復雜,攻擊的目標類型越來越豐富,目標特性越來越復雜,應用于導彈的末制導技術將向智能、精確、靈巧等方向發展,必須采用成像制導技術以滿足末端對目標準確識別捕獲及要害部位選擇攻擊的能力需求。早在20世紀80年代,美國國防部高級研究計劃局就重點發展雷達成像,并列為高靈敏度制導技術重點項目,雷達成像已經成為新一代雷達導引頭技術的重點發展方向之一。

對傳統的合成孔徑雷達成像而言,由于成像所需的多普勒差異[1]在雷達凝視或前視情況下不存在,所以要想將目標信息提取出來只能依賴實波束的功率差異,無法通過合成孔徑的多普勒分析獲取跨距離分辨能力,因此難以解決末端高精度打擊及要害部位選擇攻擊的問題。而微波雷達關聯成像則不依賴于多普勒效應,其成像原理是通過分析相控陣天線輻射的空時二維隨機散射場與場景目標相互作用[2]產生的關聯耦合,反演求解得到場景目標點散射系數,天線輻射場漲落的差異性是區分場景中目標分布信息的關鍵。

為了產生空時二維隨機漲落[3]輻射場可以采用傳統的基于相控陣移相器隨機配相的方法,但是通過一階關聯成像算法得出的圖像分辨率并不是很高,因為利用場的自相干函數對目標進行信息解耦[4]是關聯處理的實質。由于場的隨機漲落特性并沒有充分發揮作用,故而這種方法與實波束成像沒有什么區別。而采用結合壓縮感知的稀疏求解方法,不僅可以擁有突破瑞利分辨極限的能力,而且只需要使用很少的采樣數就可以恢復出目標圖像。

這幾年,激光遙感平臺上已經成功應用基于稀疏重構的關聯成像技術并且能夠實現超瑞利分辨[5]。此外,為了實現高比率數據壓縮[6],國外研究小組在微波超材料孔徑天線上也利用這項技術并獲得成功。受啟發于這些成果并且基于關聯計算的原理,本文提出了一種雷達前視成像的新方法,這種方法采用相控陣雷達,方便調控移相器來模擬經典關聯成像中的散斑場,并利用壓縮感知稀疏求解方法[7-10]使雷達成像的方位分辨力在常規實孔徑陣列中的限制得以突破。對于前視關聯成像的經典算法[11-14]——一階關聯處理算法雖然計算速度快,但是副瓣較高,成像質量較差，而本文提出的方法可以利用目標場景的稀疏性實現超分辨使成像效果提高。本文通過仿真實驗驗證了所提方法原理的正確性,并通過實測數據處理結果驗證了算法的有效性。

1 基于壓縮感知超分辨關聯成像

1.1 微波關聯成像信號模型

雷達發射天線發射的電磁波需要具有空時不相關性質[15],發射的電磁波在場景目標處散射后,接收天線接收后向電磁散射的目標回波。如圖1所示，建立一個以發射天線上任意一點作為參考點O的坐標系,如果認為是很多個點源構成了天線的輻射口面,那么天線口徑面上所有的點源在某處產生的場的疊加就可以和目標場景中某處的入射場一一對應,表示如下：

(1)

式中:rtx為發射天線口徑面上的某任意位置;rT為目標場景任意一處;Etx(rtx,t)為發射天線口面;Atx為發射天線口面;t為時間。

圖1 微波雷達關聯成像工作示意圖Fig.1 Schematic diagram of microwave radar correlation imaging

波傳播的格林函數在自由空間中的表達式為

(2)

場景中的目標散射場與天線發射出的入射場的相互作用關系可以用場景的后向散射系數分布σ(rT)來描述(利用了一階玻恩近似并忽略掉二次散射的影響),目標rT處的散射場可以表示為

Escat(rT,t)=σ(rT)Einc(rT,t)

(3)

只需要計算出目標場景中所有點的散射場在任意位置的疊加,就可以得到接收天線口徑面上該處的輻射場(假設接收天線與發射天線完全隔離)

(4)

式中:S表示目標區域。其接收到的場為自身口面的矢量場疊加,因為接收天線工作時使用的接收輻射場是空時二維完全隨機的,故其不具備空間分辨的能力,所以接收到的場可以表示為

(5)

式中：Arx(rT,t)為接收天線口面。

從之前推導可以看出，Einc(rT,t)實際上就是發射天線在rT處的輻射方向圖。而對于接收天線來說,在rT處的接收方向圖(rT處的散射場為單位1時)表示為

(6)

將Einc(rT,t)和Erec(rT,t)代入式(5)得

(7)

式中:F(rT,t)為等效的雙程天線輻射方向圖函數。

如果天線發射和接收的兩個輻射場方向圖中同時或者其中任意一個輻射場方向圖具有空時二維的隨機特性,那么這種空時二維的不相干性也同樣存在于其等效的雙程方向圖中。

(8)

然后，令天線接收到的場與等效雙程天線輻射場進行一階關聯,有：

(9)

通過上面的表達式,可以推導出目標后向散射特性分布：

(10)

上述推導過程即是利用一階矢量場進行經典關聯成像的方法,包含了從相控陣天線輻射具有空時二維隨機特性的信號,入射場與場景中的目標散射點相互作用,直到具有空時二維隨機特性散射場被相控陣天線接收的整個物理過程。

1.2 壓縮感知框架下的超分辨成像模型

為了模擬經典強度關聯成像中的隨機漲落散斑場,采用二維相控陣雷達制造偽隨機賦形波束的方法來產生隨機漲落的雷達天線輻射場[16]。

目標與隨機輻射場之間的作用以及接收機的回波接收過程,從另一個方向去看可以認為是空間波陣面的隨機編碼決定了隨機場的差異。被接收的散射回波是場與目標之間的相互作用產生的。該過程是使用這組隨機分布的字段等效于采樣基空間的代碼來完成對目標分布的隨機采樣。解碼過程就是使用已知的場分布來反演目標的散射系數。壓縮感知中的采樣理論[17-21]就是這個過程。在壓縮感知理論中,想要很好地恢復原始信號并不需要以高于(甚至可以遠低于)奈奎斯特采樣定理所需的采樣頻率對信號進行采樣,而實現這一目標只需要滿足原始信號的稀疏性和測量的非相關性,并有突破瑞利極限的能力[22-28]。

確定了信號的采樣矩陣之后就可以實現基于壓縮感知框架的超分辨關聯成像。如果忽略場景中不同目標點與收發天線的微小距離差別,即遠場平面波條件下的等效天線輻射方向圖F(rT,t)可以表示為F(θT,βT,t),其中θT為方位角,βT為俯仰角,結合式(7)得到此時的接收場為

(11)

將目標場景與方向圖離散化,得到

(12)

相控陣調制出來的隨機場在空間維度上具有相當高的關聯性,這是因為孔徑尺寸限制了這一點,從而導致采樣矩陣F是個非滿秩矩陣,其有效方程個數小于P,即求解Erx=Fσ是一個欠定問題。而壓縮感知解決的正是欠采樣問題[29-34]。因此,在原來的線性問題上加入一個正則化的約束,將之前的欠采樣問題轉化為如下的非線性優化問題:

(13)

可以通過擬牛頓算法[23]對上式進行求解,而考慮工程化的易實現性,在仿真和工程化中采用稀疏貝葉斯學習算法進行處理,得到超分辨成像結果。

2 微波關聯計算成像試驗驗證

2.1 前視三維雷達關聯成像原理

相控陣隨機饋相形成的隨機天線輻射場F(θT,βT,t)在各個距離波前平面上一致,可以把很多距離相等的波前平面記為多個的距離單元,雖然在不同的距離單元里電磁波的衰減程度不同,但是在同一個距離單元內,電磁波的衰減程度是一樣的,即距離衰減因子在同一個距離單元內是一個復常數,所以在同一個距離單元內,可以利用隨機輻射場的不相關性,對該距離單元內所有目標運用稀疏求解的方法進行二維超分辨解耦,從而提取目標散射信息。利用寬帶信號的特性,可以把不同距離的波前平面劃分成一個個的距離單元,而在每一個距離單元上都可以分析出一幅二維剖面圖,可以按照一定順序(比如沿雷達視線方向)將這一系列的圖像拼接起來,這樣就可以得到一個完整的三維圖像了。如果采用的拼接順序與天線法向一致,那么就可得到雷達前視三維圖像[35]，如圖2所示。

圖2 前視三維成像示意圖Fig.2 Diagram of forward-looking three dimensional imaging

2.2 關聯前視成像仿真與實測數據處理分析

利用上述前視三維雷達成像原理,對仿真數據進行成像。成像仿真實驗使用的場景如圖3(a)所示,在場景中心平面上,沿X和Y方向上間距為10 m和坐標原點處分布了5個點,而沿Z軸方向(雷達視線方向)的3個點間距為5 m,帶寬B為100 MHz,場景中心距離Rs為1 km,脈沖重復周期為16 kHz,脈沖寬度Tp為6 μs,陣列長度D為0.32 m,并在回波數據中加入高斯白噪聲以改變信噪比。理論上,發射信號帶寬和相控陣天線孔徑大小決定了實孔徑三維成像分辨率。根據仿真實驗所設定參數,距離向分辨率為1.5 m,X方向和Y方向分辨率均為53.57 m,而仿真實驗中場景的點目標空間間隔只有10 m,遠小于上述X與Y方向的理論最小可分辨距離。如圖3(b)所示的實孔徑掃描成像結果,無法分辨出中心參考距離面上的散射點。

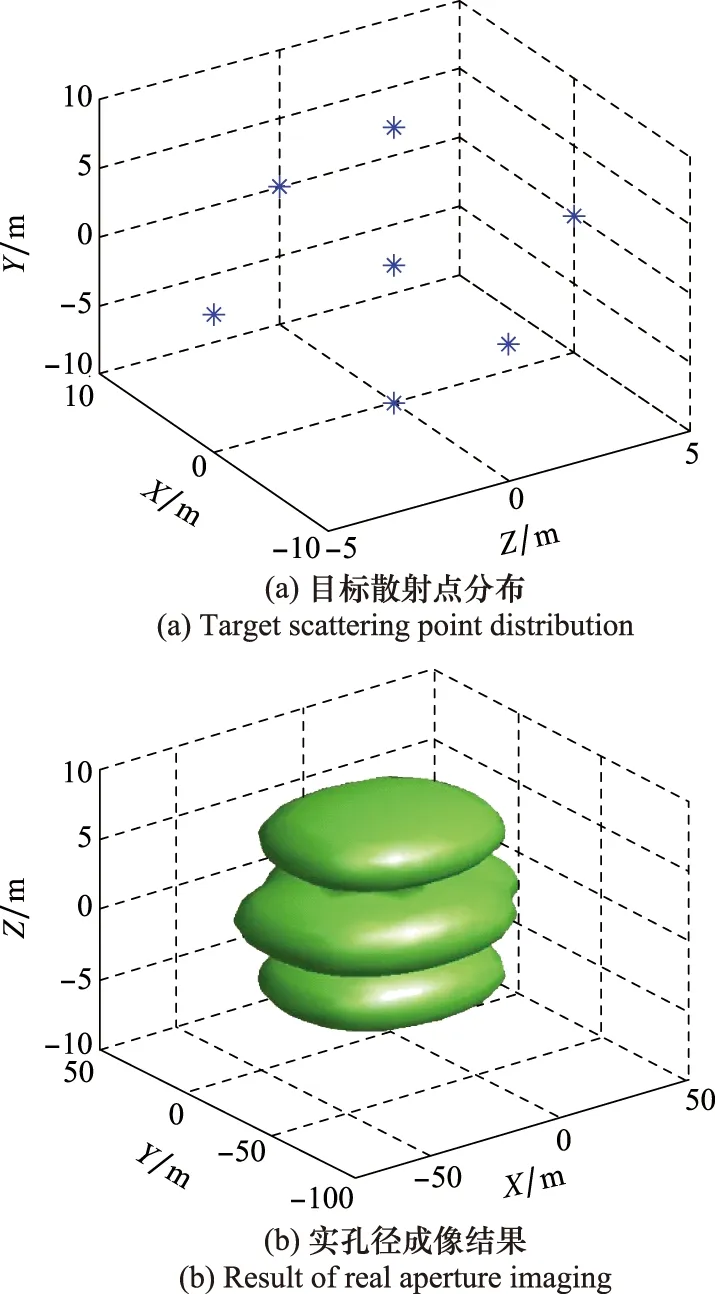
圖3 目標散射點分布與實孔徑成像結果Fig.3 Result of target scattering point distribution and real aperture imaging

基于稀疏重構的三維超分辨成像結果如圖4所示,脈沖次數是80。可以有效地分辨常規實孔徑方法無法區分的散射點,散射點噪聲和旁瓣都得到有效抑制,且位置估計準確。

為了進一步驗證關聯成像原理可行性,利用相控陣雷達進行外場成像試驗驗證，如圖5與圖6所示。目標場景中布置有4個反射體,1號反射體與雷達的距離為324 m；2號、3號和4號反射體與雷達的距離為405 m。試驗中距離向分辨率為20 m,其中400 m距離處方位波束橫向覆蓋約17 m,方位波束寬度為2.5°。成像場景設3種,反射體2、3與4號的距離R依次為17 m、8 m和4 m，最終成像結果如圖7所示。

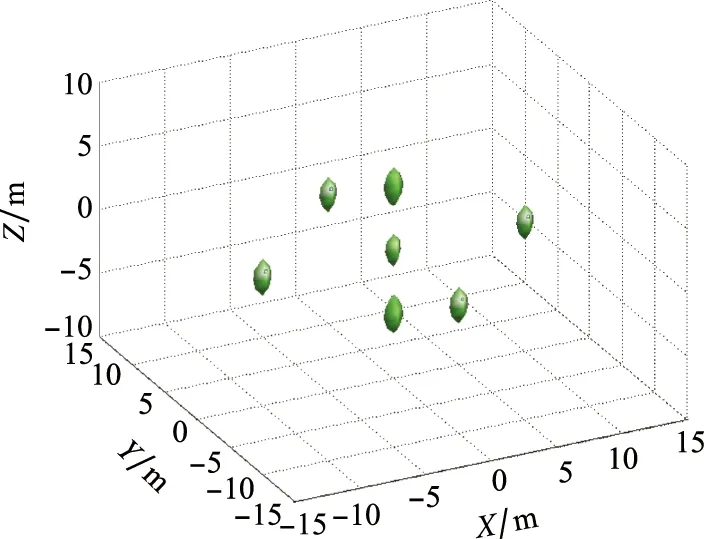
圖4 前視三維超分辨成像結果Fig.4 Result of forward-looking three-dimensional super resolution imaging

圖5 成像場景Fig.5 Imaging scene

圖6 目標場景Fig.6 Target scene

圖7 前視靜態試驗成像結果Fig.7 Result of forward-looking static test imaging

可以看出,成像結果精準體現出了場景中幾個比較明顯目標的位置,但圖像并不能展現出目標更為精細的幾何輪廓,因為場景中目標散射特性比較復雜而且成像分辨率不足，還有較多虛假點。當反射體2號、3號與4號的距離R變小時,目標依然能夠體現出來,但是隨著R變小,虛假點也在逐步增多,可能是由于有源相控陣天線幅相調節誤差和稀疏重構算法本身的缺陷導致了虛假點數目變多。總體而言,該實驗驗證了前視關聯成像原理的可行性,但針對復雜場景的高分辨成像性能及算法優化工作還需要進一步研究。

按照給出的仿真參數,理論上的分辨率應該為

(14)

式中：λ為信號波長；Rs為雷達與場景中心的距離；D為雷達孔徑長度。從圖7的成像結果來看，圖7(a)可以分辨距離為17 m的物體,實現了1.176倍超分辨；圖7(b)可以分辨距離為8 m的物體,實現了2.5倍超分辨；圖7(c)可以分辨距離為4 m的物體,實現了5倍超分辨。故本方法至少可以實現5倍超瑞利極限分辨率。

3 結 論

基于關聯計算的原理,本文提出了一種適用于相控陣雷達的前視成像方法,模擬經典關聯成像中隨機場的方法是模擬出隨機電磁輻射場,而這個輻射場是通過控制移相器實現隨機相移來產生的,最后求解目標場景中的散射系數利用了稀疏求解的方法,得到的結果即為成像結果。成像結果可以使方位分辨率突破常規實孔徑陣列雷達的限制,并將這種關聯技術推廣到前視三維成像中。雖然該方法可以實現超分辨,但是仍然有許多限制條件,比如相控陣的尺寸和自由度。故而進一步提高到10倍以上量級的超分辨是很艱難的,只有尋找到突破尺寸限制的輻射場隨機調制方法才有可能進一步提高超分辨的倍數。另外,由于成像分辨率在壓縮感知框架下沒有解析表達式指導系統設計,故只能通過實驗來嘗試測量其分辨率的大小。算法方面,也有很多亟待解決的問題,例如如何適應復雜場景的環境、如何不過分依賴場景的稀疏先驗信息和如何自動選取正則化參數等,這些問題都需要后續做進一步深入研究。