工作面煤壁振動信號分析

劉泗斐，師 鵬，萬志軍，呂嘉錕，盧帥峰，王業常

(1. 中國礦業大學 礦業工程學院，江蘇 徐州 221116；2. 福興集團有限公司，山東 棗莊 277300 )

動力擾動是煤礦生產中必不可少的現象[1]，其 產生的應力波在煤體內傳播，促進煤巖裂隙演化，進而誘導煤巖損傷并發生失穩破壞[2-3]。大的動力擾動，如采動[4]、爆破破巖[5]等，對煤層輸入能量較大，能引起煤巖較大的動力響應，并可能引發沖擊礦壓和煤與瓦斯突出等動力災害的現象已在試驗和現場得到證明[6-8]。實際工程中，某些較小的動力擾動，如割煤、打鉆[9]等，也能誘使煤巖發生破 壞[10-11]，甚至促發煤巖動力災害，卻經常被忽 視[12]。但隨著對深部高能位煤層動力災害發生機理研究的加深，這些較小的擾動也逐漸被認識，特別是割煤因素已逐漸進入研究視野[12-13]。動力擾動在使礦山應力重新分布的同時[14]，也造成煤巖強度弱化[4]，在工作面與掘進頭形成較大范圍的松動圈，降低機具截割難度，給生產帶來便利。特別是某些低能量擾動，在高應力環境中可以使巖石內部裂紋得到有效擴展，誘導巖石破壞且效果明顯[15-17]。綜上所述，小擾動對生產具有明顯的兩面性，既能觸發煤巖動力災害，也能降低煤巖截割難度，因此，有必要加強對其的認識。

有學者試圖提取井下割煤作業的振動信號，但經過多種變換未能獲取較為清晰的數據[18]，因此獲取井下煤壁振動信號是非常困難的。本文借助國家能源采掘裝備研發中心的煤機裝備試驗系統，采集了割煤作業在煤壁產生的振動信號，分析了工作面不同割煤工況下煤壁的振動特性，并應用此振動誘導高能位煤巖破壞，為提出弱化割煤誘發動力災害的建議和提高微擾動破巖效率的方法提供基礎依據。

1 煤機裝備試驗

1.1 試驗系統

綜采工作面模擬煤壁是以煤作為骨料，長70 m、高3 m[18]。TDS微震地面采集系統由總站與分站組成，系統通過無線方式形成觀測網絡，采樣頻率是1 kHz。圖1為采掘裝備綜合實驗室及微震采集系統。

圖1 采掘裝備綜合實驗室及微震采集系統 Fig. 1 Comprehensive laboratory of mining equipment and microseismic acquisition system

1.2 試驗方案

振動對煤巖體穩定性的影響程度不僅取決于激勵源的能量和形式，同時也與煤巖體的部分固有特性，特別是自振頻率等參數密切相關[19]，為此先采集煤壁的自振特征，然后再采集割煤作用下的振動特征。將布置好的采集系統在無任何采煤動作下記錄數據，采集煤壁結構的自振特征；然后分別記錄截割深度為300 mm工況下、采煤機速度為0，1.5，2.0，3.0和5.0 m/min的煤壁振動數據，最后進行斜切進刀( S形 )工況下、采煤機速度為0，1.5，3.0和4.8 m/min的煤壁振動特征測試。

2 煤壁振動信號HHT分析

2.1 煤壁振動信號Hilbert譜[18,20]

希爾伯特黃變換( Hilbert-Huang Transform，簡稱HHT )是由EMD分解與Hilbert變換組合而成。因EMD分解不需先驗基底，使其具有很強的自適應性，特別是對隨機信號的處理具有很大優勢；同時，經EMD分解得到的IMF分量更具有明顯的物理意義，Hilbert譜能夠真實地反映振動過程中的能量在各種尺度或頻率及空間或時間上的分布規律。

2.1.1 煤壁振動信號EMD分解與信號重建

EMD是HHT變換的核心，煤壁振動信號經過EMD分解可以得到n階IMF分量和殘差rn(t)之和，然后根據IMF與振動信號的相關性與方差貢獻率，消除噪音對振動信號的影響。振動信號計算公式為

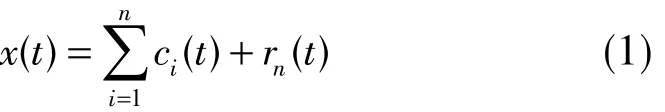
式中，x(t)表示振動信號；ci(t)表示第i個IMF分量；rn(t)表示殘余信號。

本文以采煤機直行速度3 m/min工況為例，在測站1中選取較為穩定的10 s信號，經過EMD分解，共得到11個IMF值，如圖2所示。經過對IMF與數據的相關性分析，發現IMF1，IMF3，IMF4和IMF5與原始信號有較大的相關性，其方差貢獻和為95.51%，且單項貢獻率均在10%以上( 見表1 )。其他IMF分量幅值小且貢獻率低，為噪音分量。舍棄噪音分量，將分量IMF1，IMF3，IMF4和IMF5重構獲取煤壁振動新信號，與原始信號進行相關性分析，相關系數為97.55%，結果表明重構信號效果較好、可靠。

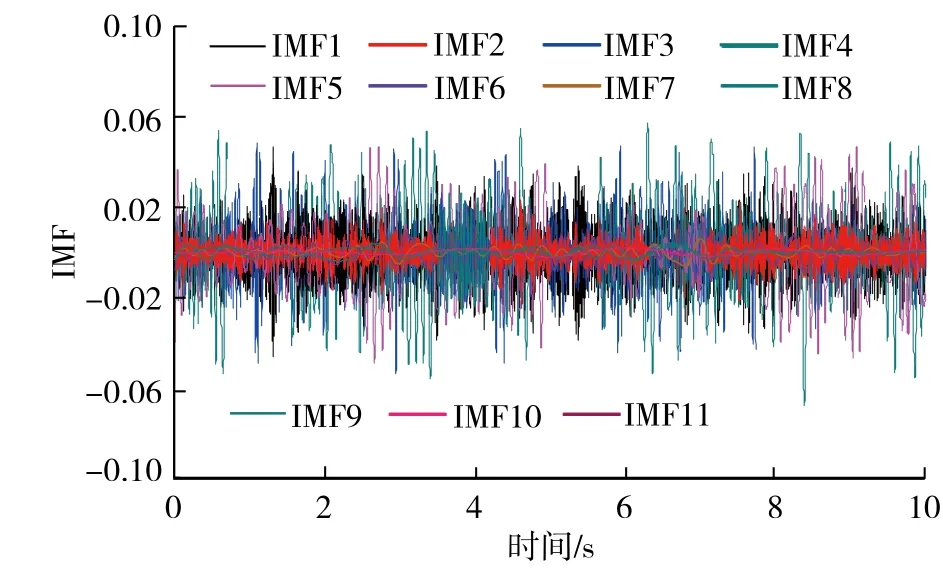
圖2 IMF分量圖 Fig. 2 IMF component diagram

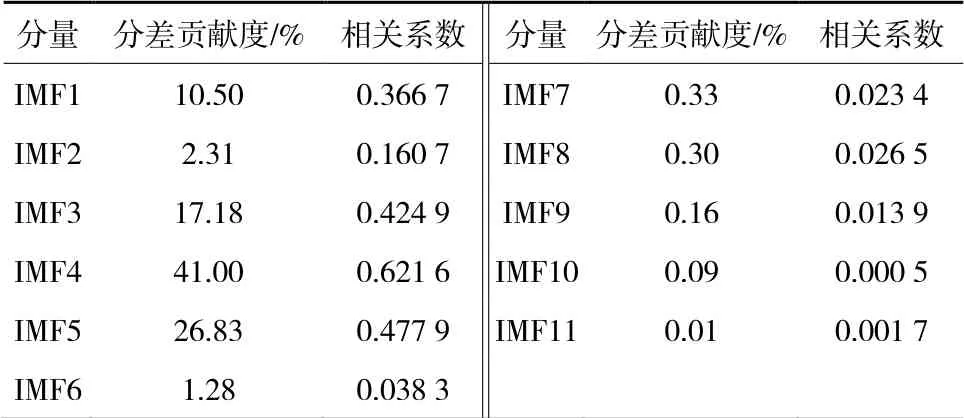
表1 IMF分量與原始信號的相關性 Table 1 Correlation between IMF component and original signal

2.1.2 煤壁振動信號Hilbert譜

對原始信號的每一個IMF進行Hilbert變換，可得到

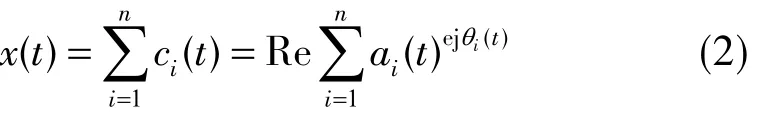
式中，略去了rn(t)，Re為實部，ai，θi為常數，ai(t)為幅值函數；jθi(t)為頻率函數，θi(t)可表示為θi(t) =∫ωi(t)dt。

將瞬時幅值、瞬時頻率隨時間的變化在圖中表示出來，這個幅值在時域和頻域的分布就是x(t)信號的Hilbert譜，基座H(ω，t)。

本文以煤壁振動激勵源信號、自振、采煤機直行割煤速度3 m/min和斜切進刀( S彎 )速度3 m/min的工況為例，分別選取測站1較為穩定的10 s數據進行分析。

在割煤作用下，煤壁振動信號的Hilbert譜如圖3所示。整體來看，信號分為2個頻帶，主要集中在低頻帶7～12 Hz，表明擾動信號與自振信號易發生共振。在頻帶I中，自振信號沒有明顯的載波特性，割煤信號比自振主頻低但幅值大，表明機械工作迫使煤巖發生較大幅值的振動；在頻帶II中，斜切進刀信號的強度在12～18 Hz間大于直行割煤，而在18～27 Hz段相反，表現出不同割煤方式不同擾動的特點。

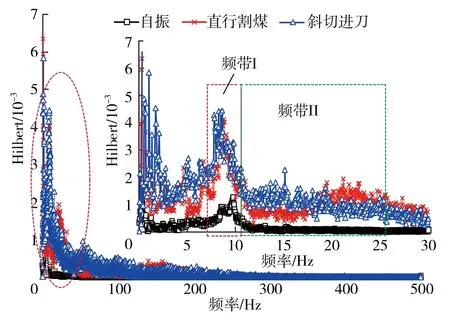
圖3 割煤時煤壁振動信號的Hilbert譜 Fig. 3 Hilbert spectrum of vibration signal of coal wall during coal cutting

2.2 不同工況煤壁振動信號能量分析

由EMD-HHT信號分析理論可知，振動信號的瞬時能量、邊際能量反映了幅值與時間、振動頻率的關系，對瞬時能量、邊際能量進行分析研究有利于揭示振動效應的本質。

對每個分量進行變換后Hilbert變換得到信號的譜，在頻域內并對Hilbert幅值的平方進行積分，得到信號的瞬時能量為

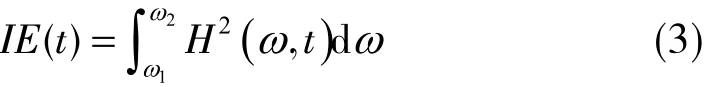
同理，在時域內對幅值的平方進行積分得到信號的邊際能量為

對IE在時域、ES在頻域進行積分可得到信號的能量為

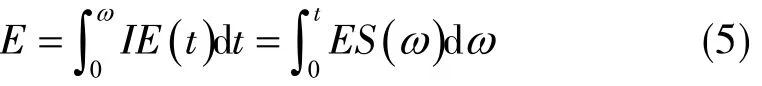
以采煤機直行割煤速度3 m/min與空載和斜切進刀( S彎 )速度3 m/min與空載的工況為例，在測站1中分別選取較為穩定的10 s數據進行煤壁振動信號的邊際能量分析，得到如圖4，5所示結果。

邊際能量圖描述了振動能量隨頻率的分布情況。由圖4，5可知，① 直行割煤與斜切進刀在空載時的能量最大值要大于重載的幅值，但相差不大；

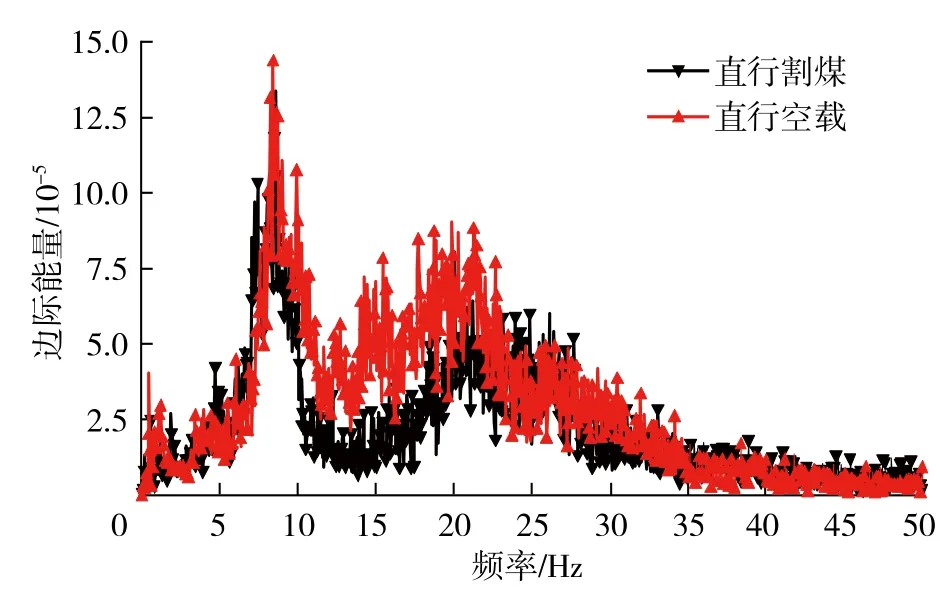
圖4 直行割煤與空載邊際能量 Fig. 4 Straight cutting coal and no load marginalenergy diagram

圖4中直行割煤與直行空載時有2個能量頻帶，分別集中在7～12和18～30 Hz，其中低頻帶能量大于高頻帶。圖5中斜切進刀的振動能量集中在7～12 Hz，雖在12～30 Hz之間也有部分能量分布，但為7～12 Hz能量分布的延續，因此斜切進刀振動信號只有1個能量頻帶。這是因為，在高頻帶中的能量主要是由于采煤機行走產生的，在斜切進刀時，采煤機受到刮板輸送機的側向力作用，加大了采煤機的不平衡力，產生了更大振動；同時刮板輸送機鏈條受到采煤機的反作用，也加大了鏈條的振動，因此在斜切進刀時在12～18 Hz之間沒有明顯的能量減少。

圖5 斜切進刀割煤與空載邊際能量 Fig. 5 Coal cutting with oblique feed and no load marginal energy

2.3 不同截割速度煤壁振動信號能量分析

從總體特征來看，邊際能量幅值變化規律較為一致( 圖6 )，集中出現在6～15和15～30 Hz兩個頻帶，顯示出同增共減的特點，表明4種信號在振動本質上一致。從局部對比來看：① 在6～15 Hz中，2 m/min信號的邊際能量幅值表現異常，不足其他信號的1/2，對多組2 m/min信號的邊際能量做分析，其規律保持不變，究其原因為2 m/min速度下工作面不同設備間發生了振動疊加，減弱了煤壁的振動，說明2 m/min的割煤速度可以弱化邊際能量。② 在15～30 Hz頻帶上，能量幅值隨著割煤速度的增加而增大，表明振動信號與割煤速度呈正相關關系。

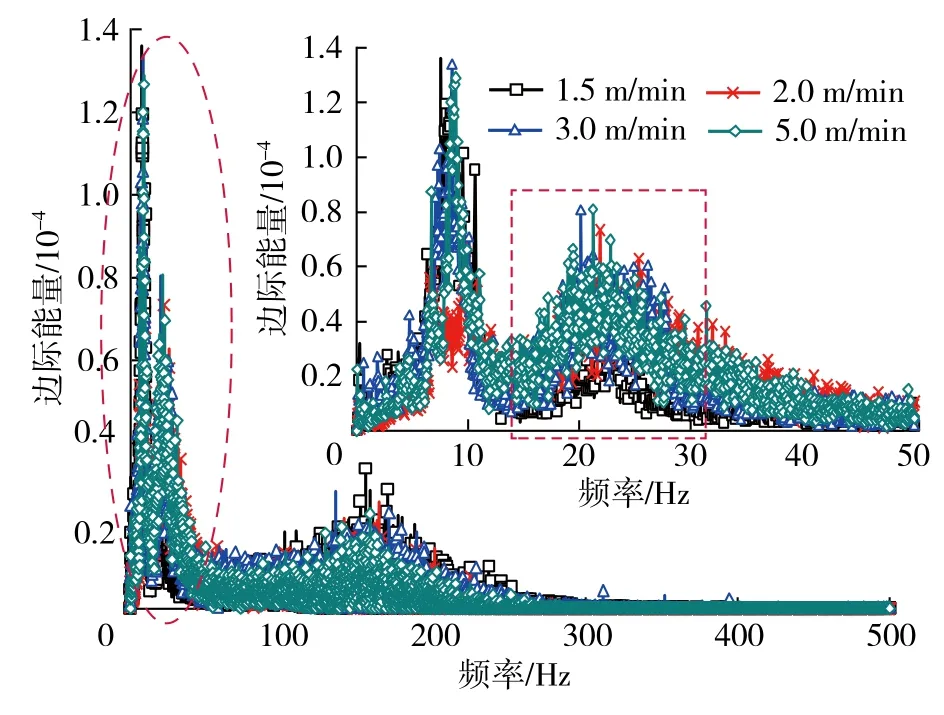
圖6 不同割煤速度煤壁信號邊際能量 Fig. 6 Marginal energy diagram of coal wall signal at different cutting speeds

3 微擾動誘導高能位煤巖破壞數值模擬

本文以鮑店煤礦煤樣的實驗參數為基礎，借助PFC2D5.0軟件的平行粘結模型建立50 mm×100 mm的煤巖試樣，如圖7所示。試樣的顆粒半徑為0.34～0.56 mm，共10 768個球，具體力學參數見表2，單軸抗壓強度為19.3 MPa。

圖7 第1加載階段完成 Fig. 7 First loading phase is completed

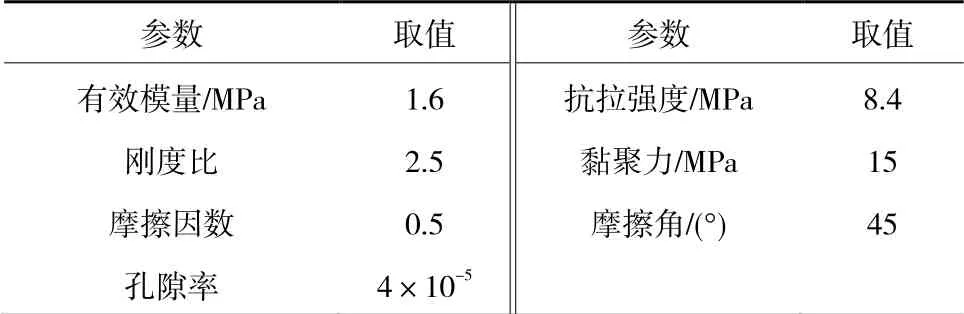
表2 PFC微觀力學參數 Table 2 Micromechanical parameters of PFC

首先調用上述單軸實驗中的試樣，然后利用FISH語言控制PFC2D的伺服機構將試樣加載至高能位( 屈服點 )，再通過位移控制加載0.5 mm的微振動，即0.5%的應變，周期為10 Hz，得到結果如圖8，9所示。

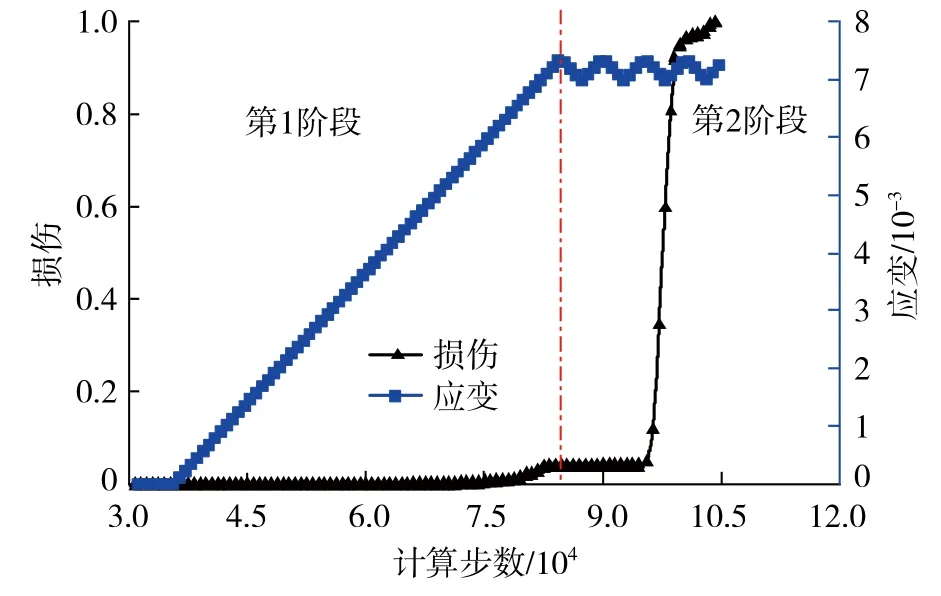
圖8 位移與損傷 Fig. 8 Displacement and damage

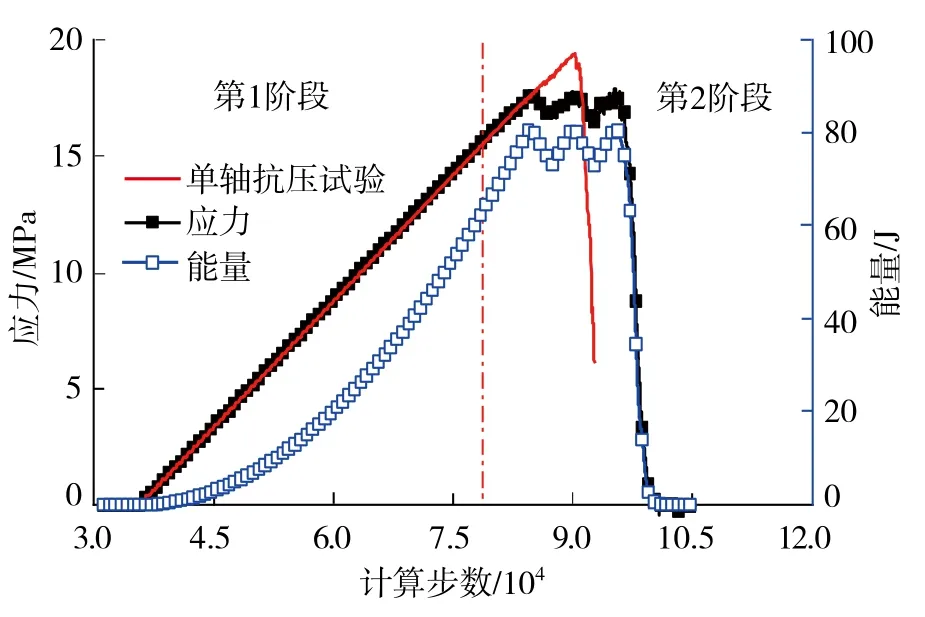
圖9 應力與能量 Fig. 9 Stress and energy

圖8，9描述了整個加載過程的軸向位移、應力、彈性能和試樣的損傷情況，其中第1階段為位移控制加載，加載至試樣損傷( 裂隙 )出現，即認為進入試樣的屈服階段，如圖7所示，在此階段內，應力與試樣內彈性能不斷增加；第2階段為位移控制的微擾動，應力呈非線性變化，能量隨其波動。

圖9顯示，在靜載作用下，促使試樣裂紋發展、破壞失穩的應力幅值為19.3 MPa，小于此值的應力將不會導致裂紋的產生或擴展。然而，高能位煤巖試樣在微擾動載荷下，雖然應力值未達到單軸抗壓強度，但經過多次擾動，裂紋的發育與擴展卻開始出現，最終實現煤巖的完全破壞，如圖10所示，動態破壞顯著區別于靜態破壞，破壞程度更嚴重。這表明，微擾動可以加強煤巖破壞的趨勢，提高煤巖的破碎效率。

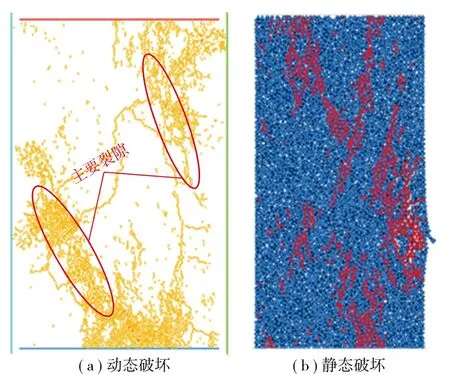
圖10 試樣破壞狀態 Fig. 10 Failure state of specimen

4 結 論

( 1 ) 割煤信號屬于低頻擾動，易與煤壁發生共振。EMD對割煤振動信號進行了較好的分解和噪音消除，重構信號與原始信號相關系數為97.55%。在Hilbert譜中顯示，割煤對煤壁振動的影響較大，迫使煤壁發生較大幅值的振動，能量主要集中在7～12 Hz，與煤壁自振頻率相近，易發生共振。

( 2 ) 不同采煤工況具有不同的擾動信號。① 直行割煤與斜切進刀在空載時的能量最大值要大于重載的幅值，但相差不大；② 斜切進刀的能量幅值比直行割煤的幅值要大；③ 不同割煤速度下擾動信號邊際能量變化的趨勢較為一致，能量隨割煤速度的增大而增加。

( 3 ) 高能位煤巖能在微擾動誘導下發生破壞。利用PFC2D將試樣加載至高能位狀態，然后加載頻率為10 Hz的微擾動，經過多次作用，使煤巖在未達到單軸抗壓強度下發生破壞，表現為微擾動誘導高能位煤巖破壞，表明低能量擾動能提高深部煤巖的破巖效率。