定子電流信號中的齒輪故障過調(diào)制特征及二次幅值解調(diào)分析

時獻(xiàn)江，李洪建，郭華，司俊山

(哈爾濱理工大學(xué) 機(jī)械動力工程學(xué)院，哈爾濱 150080)

0 引 言

電機(jī)定子電流信號分析方法(motor current signature analysis,MCSA)的基本原理是將電機(jī)本身作為一種能夠?qū)崿F(xiàn)電磁轉(zhuǎn)矩估計的扭矩傳感器，利用電流傳感器就可以直接實現(xiàn)電機(jī)及其傳動系統(tǒng)的故障診斷[1]。相對于傳統(tǒng)的振動檢測方法，MCSA方法采用磁電感應(yīng)方式獲取定子電流信號，是電信號到電信號的直接變換，具有信號獲取簡便、魯棒性好和成本低等優(yōu)點。目前，在電動機(jī)轉(zhuǎn)子偏心、斷條等故障診斷方面獲得廣泛應(yīng)用。近年來，有關(guān)電機(jī)傳動鏈齒輪的故障診斷研究文獻(xiàn)也越來越多，例如傳統(tǒng)的工業(yè)傳動設(shè)備[2]、電氣列車或動車組[3-4]，甚至還有風(fēng)力發(fā)電機(jī)[5-6]等新型裝備。

但是，目前診斷與分析效果比較明顯的文獻(xiàn)多為特殊情況下的研究成果。如文獻(xiàn)[7]通過監(jiān)控?zé)o刷直流電動機(jī)電流信號來檢測汽車動力轉(zhuǎn)向系統(tǒng)中的蝸輪齒面故障；文獻(xiàn)[8]檢測永磁同步發(fā)電機(jī)定子電流信號中的增速齒輪故障特征；文獻(xiàn)[9]利用一個大減速比水泥窯傳動試驗裝置，研究低速齒輪故障特征在傳動鏈遠(yuǎn)端驅(qū)動電動機(jī)定子電流信號中的反映。MCSA方法主要依靠電源頻率信號承載或調(diào)制機(jī)械故障引起的定子電流變化成分，此時電源頻率為載波頻率，機(jī)械故障頻率為調(diào)制頻率。在上述研究中，由于定子電流信號的電源頻率高[7,8]，或者是齒輪故障特征頻率低[9]，使得故障頻率遠(yuǎn)遠(yuǎn)小于載波頻率。此時，即使不采用特殊的信號處理手段，在原始頻譜上也可以直接獲得齒輪的故障頻率或者嚙合頻率成分。

但是，在通常情況下，電源供電頻率≤50 Hz，傳動系統(tǒng)的齒輪嚙合頻率往往遠(yuǎn)大于電源供電頻率，此時信號處于“過調(diào)制”狀態(tài)[10]。另外，齒輪嚙合頻率本身還調(diào)制有齒輪故障頻率成分，在這種雙重調(diào)制的共同作用下，齒輪定子電流信號的調(diào)制邊帶成分往往存在諧波復(fù)雜、階次多等問題[11-14]，分析效果遠(yuǎn)不如文獻(xiàn)[7～9]所敘述的那么明顯，甚至在能否檢測到齒輪嚙合頻率成分這一問題上，各個文獻(xiàn)之間的結(jié)論也不完全一致[11,15]。

“過調(diào)制”現(xiàn)象是MCSA方法分析齒輪、軸承類傳動系統(tǒng)零部件故障時必然遇到的問題，目前關(guān)于齒輪方面的相關(guān)研究文獻(xiàn)幾乎為空白。為此，本文首先從全局域雙邊頻譜分析方法入手，研究電動機(jī)定子電流信號中的齒輪故障過調(diào)制及雙重調(diào)制現(xiàn)象的成因及規(guī)律，提出一種二次幅值解調(diào)分析的齒輪故障特征提取方法。然后利用計算機(jī)仿真和模擬試驗方法，模擬與重現(xiàn)齒輪故障時的定子電流信號過調(diào)制特征，驗證二次幅值解調(diào)分析方法的有效性，解決定子電流信號頻譜中存在的諧波成分復(fù)雜，齒輪故障特征不易識別等問題。

1 電動機(jī)驅(qū)動齒輪傳動動力學(xué)分析

1.1 動力學(xué)模型

電動機(jī)驅(qū)動一個減速直齒輪傳動副的動力學(xué)模型如圖1所示，如僅以電動機(jī)及小齒輪為研究對象，其動力學(xué)微分方程為

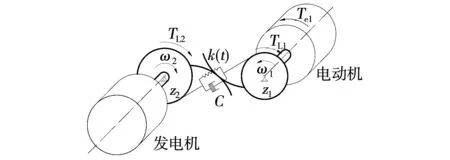
圖1 電動機(jī)驅(qū)動齒輪傳動副的力學(xué)模型Fig.1 Mechanical model of gear drive pair driven by motor

eF(t))=TL1-Te1。

(1)

式中：θ1(t)為小齒輪的扭轉(zhuǎn)振動相對角位移；J1為小齒輪和驅(qū)動電動機(jī)的轉(zhuǎn)動慣量；C為齒輪嚙合阻尼；k(t)為齒輪嚙合剛度；r1為小齒輪節(jié)圓半徑；eS為齒輪受載后的平均靜彈性變形；eF(t)為齒輪誤差和故障引起的，沿兩個齒輪間嚙合線方向的相對位移；TL1為負(fù)載發(fā)電機(jī)產(chǎn)生的負(fù)載轉(zhuǎn)矩；Te1為電動機(jī)的電磁轉(zhuǎn)矩。

系統(tǒng)穩(wěn)定時，負(fù)載轉(zhuǎn)矩TL1等于電磁轉(zhuǎn)矩Te1，式(1)變?yōu)?/p>

r1k(t)(eS+eF(t))。

(2)

該式為典型的受迫振動方程，此時齒輪系統(tǒng)的振動特性取決于式(2)右側(cè)的激振力矩函數(shù)。

1.2 嚙合剛度及接觸激振力矩估算

激振力矩函數(shù)與齒輪的嚙合剛度及變形有關(guān)，嚙合剛度k(t)與齒面接觸應(yīng)力分布形式和齒輪結(jié)構(gòu)形狀有關(guān)。一般來說，直齒輪的嚙合剛度變化劇烈，如圖2(a)所示，理想狀態(tài)下可近似用矩形波描述；斜齒輪由于重合度大，剛度變化緩慢，可用簡諧函數(shù)表示，如圖2(b)所示。

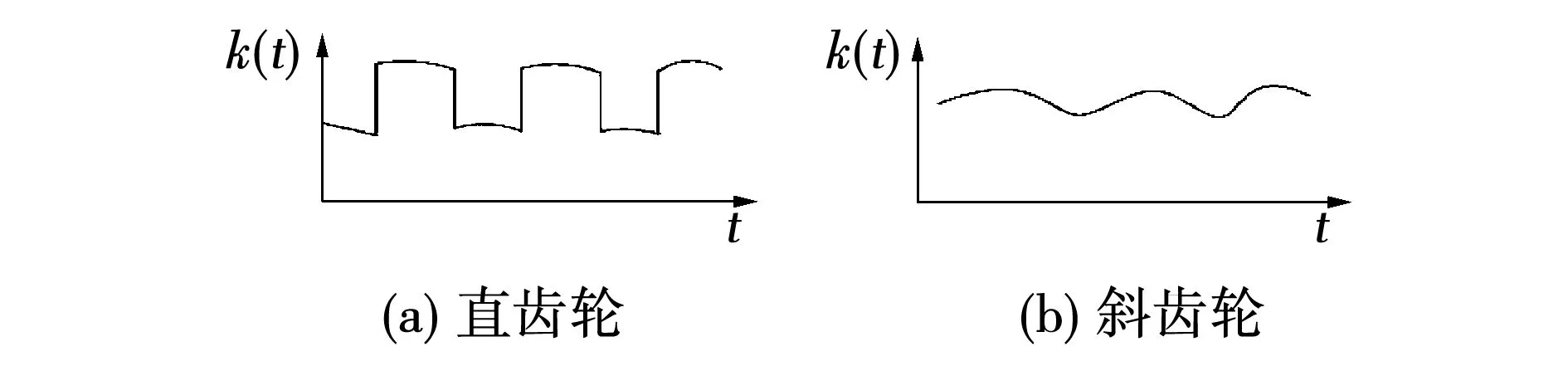
圖2 齒輪嚙合剛度變化曲線示意圖Fig.2 Gear meshing stiffness curve

但是，式(2)無法估計故障齒面嚙合時產(chǎn)生的沖擊力矩，此時，可以根據(jù)Hertz彈性接觸沖擊理論估計，如果忽略阻尼，兩個輪齒之間的法向接觸力沖擊為[16]

(3)

式中：δ為接觸點的法向位移或變形(mm)；k為接觸剛度(N/mm)。k取決于沖擊物體的材料和結(jié)構(gòu)形狀，有多種近似計算方法，本文參考文獻(xiàn)[16]，使用ISO 經(jīng)驗公式計算。

當(dāng)采用標(biāo)準(zhǔn)直齒輪時，輪坯結(jié)構(gòu)系數(shù)CR可取為1，基本齒條系數(shù)CB=1.125，假設(shè)試驗修正系數(shù)CM=1，小齒輪齒數(shù)z1=23，大齒輪齒數(shù)z2=34，模數(shù)為3，寬度為b=20 mm，可計算單對齒接觸剛度c′=3.38×105N/mm。當(dāng)齒輪端面重合度εα=1.38時，計算綜合嚙合剛度Cγ=4.35×105N/mm。

若以單對齒接觸剛度c'為嚙合剛度最小值kmin，以綜合嚙合剛度Cγ為嚙合剛度最大值kmax，可構(gòu)造理想情況時的嚙合剛度變化曲線k(t)如圖3(a)所示。其為一個占空比為50%的方波，其中tm為k(t)的變化周期，tm=1/fm，fm為k(t)的變化頻率，即齒輪嚙合頻率。

另外，可以根據(jù)齒輪承受的恒定載荷計算齒面靜態(tài)接觸變形量eS。由Hertz接觸理論可知，互相接觸的2個同材質(zhì)旋轉(zhuǎn)體接觸點的接觸變形eS可采用如下公式計算：[17]

(4)

式中：P為靜載荷；R1、R2為兩接觸體在接觸點的曲率半徑；μ和E為相應(yīng)材料的泊松比和彈性模量。

由于齒輪的齒高和分度圓半徑相比較小，可以用大、小齒輪節(jié)圓半徑r2和r1代替R2和R1；齒輪材料為45#鋼，μ=0.3，E=2.04×105N/mm2；假設(shè)齒輪傳遞TL1=5 N·m的恒定轉(zhuǎn)矩，此時，P=TL1/r1=114.93 N。于是，由式(4)計算得基本接觸靜變形eS=3.58×10-3mm。

假設(shè)單個齒面故障引起的誤差eF=0.01 mm，此數(shù)值非常小，可將其也視為變形量來一起估算由此產(chǎn)生的沖擊力矩。于是，齒輪嚙合過程中的最大變形量δmax=eS+eF，最小變形量δmin=eS，其變化過程可用δ(t)曲線(圖3(b))所示，其中，tr為故障齒輪的旋轉(zhuǎn)周期，tr=1/fr，fr為其旋轉(zhuǎn)頻率。

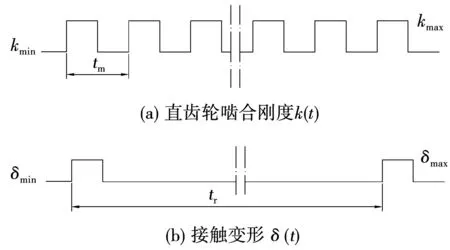
圖3 計算嚙合剛度變化曲線和接觸變形變化曲線Fig.3 Calculation of meshing stiffness curve and contact deformation curve

根據(jù)上述計算結(jié)果以及式(2)，電動機(jī)側(cè)齒輪所受激振力矩變化函數(shù)為

(5)

式右端為k(t)和δ(t)的調(diào)制函數(shù)。由于兩者均為方波函數(shù)，可見這是一種多階的調(diào)制關(guān)系。

2 定子電流信號響應(yīng)及過調(diào)制特征

2.1 定子電流信號中的故障特征頻率

根據(jù)定子電流信號調(diào)制原理，式(5)右側(cè)所示的激振力矩特征會以多階的fm±fr成分總體調(diào)制在電源主頻率上，形成雙重調(diào)制關(guān)系。考慮到電源頻率上還可能存在直接的齒輪故障調(diào)制成分fr，于是，定子電流信號中的齒輪故障調(diào)制頻率[1]表達(dá)式為：

f=|fs±m(xù)fm±nfr|；f=|fs±m(xù)fr|。

(6)

式中：fs為電動機(jī)的供電電源頻率；m，n為調(diào)制頻率諧波次數(shù)，m，n=1，2，3.…。

1.2 齒輪嚙合頻率的定子電流過調(diào)制特征及二次幅值解調(diào)原理

理想情況時的齒輪定子電流信號雙邊頻譜如圖4(a)所示。正頻率段的單邊譜包括電源頻率fs及其齒輪故障頻率fr調(diào)制邊帶和齒輪嚙合頻率fm(及其fr調(diào)制邊帶族)兩大部分。前者為正常調(diào)制，載波頻率fs<調(diào)制頻率fr，fr對稱處于fs兩側(cè)；后者雖然也存在兩個調(diào)制邊帶族|fs±fm|，但是并不對稱。原因是齒輪嚙合頻率fm已經(jīng)遠(yuǎn)大于電源頻率fs，超出常規(guī)的幅值調(diào)制的定義，為了區(qū)別起見，稱之為“過調(diào)制”。過調(diào)制時fs的左側(cè)邊帶(fs-fm)<0，無法在正頻率軸表示，一般文獻(xiàn)只能取式(6)的絕對值結(jié)果|fs-fm|來表示。

如果我們換一種角度去觀察圖4(a)的全域雙邊譜，并以實線表示正頻率軸的fs及其調(diào)制成分，虛線表示負(fù)頻率軸的-fs及其調(diào)制成分。根據(jù)實信號的正負(fù)頻率成分對稱性，可以發(fā)現(xiàn)過調(diào)制信號仍然具有普通調(diào)制信號的邊帶對稱性。此時，正頻率軸處的|fs-fm|只不過是負(fù)頻率軸的載波頻率-fs的右側(cè)fm邊帶(-fs+fm)罷了，因此，我們稱其為過調(diào)制折疊頻率。實際上，對于齒輪信號，由于fm本身還有多階fr調(diào)制成分，過調(diào)制折疊頻率是一簇頻譜成分，見圖4(a)所示。

如果直接對過調(diào)制信號進(jìn)行幅值解調(diào)分析，可得圖4(b)所示的一次幅值解調(diào)譜，其中fr、fm及其邊帶為正常解調(diào)結(jié)果。但是，過調(diào)制折疊頻率|fs-fm|及其邊帶卻也作為fs的差頻成分fm-2fs被解調(diào)出來了，顯然這個頻率成分是不存在的，是由于過調(diào)制折疊頻率產(chǎn)生的虛假解調(diào)頻率成分。實際上，齒輪信號的虛假解調(diào)頻率fm-2fs也包括一簇邊帶成分(圖4(b))，加之fs本身調(diào)制的fr還有諧波成分存在，這些頻率成分在fr至fm區(qū)間內(nèi)可能產(chǎn)生交叉、疊加，導(dǎo)致包絡(luò)譜或幅值譜的低頻段出現(xiàn)大面積的以fr為間隔的譜峰群[11-14]，使得齒輪故障特征難以識別與提取。

此時，我們可以利用遠(yuǎn)離這些頻率混疊區(qū)域的、高頻段的fm及其邊帶進(jìn)行解調(diào)分析。首先通過帶通濾波獲得中心頻率fm及其附近的若干階fr邊帶成分(圖4(c))，然后，對其做兩次幅值解調(diào)分析，解除存在的雙重調(diào)制關(guān)系，即可獲取準(zhǔn)確的、且易于識別的齒輪故障特征頻率fr。

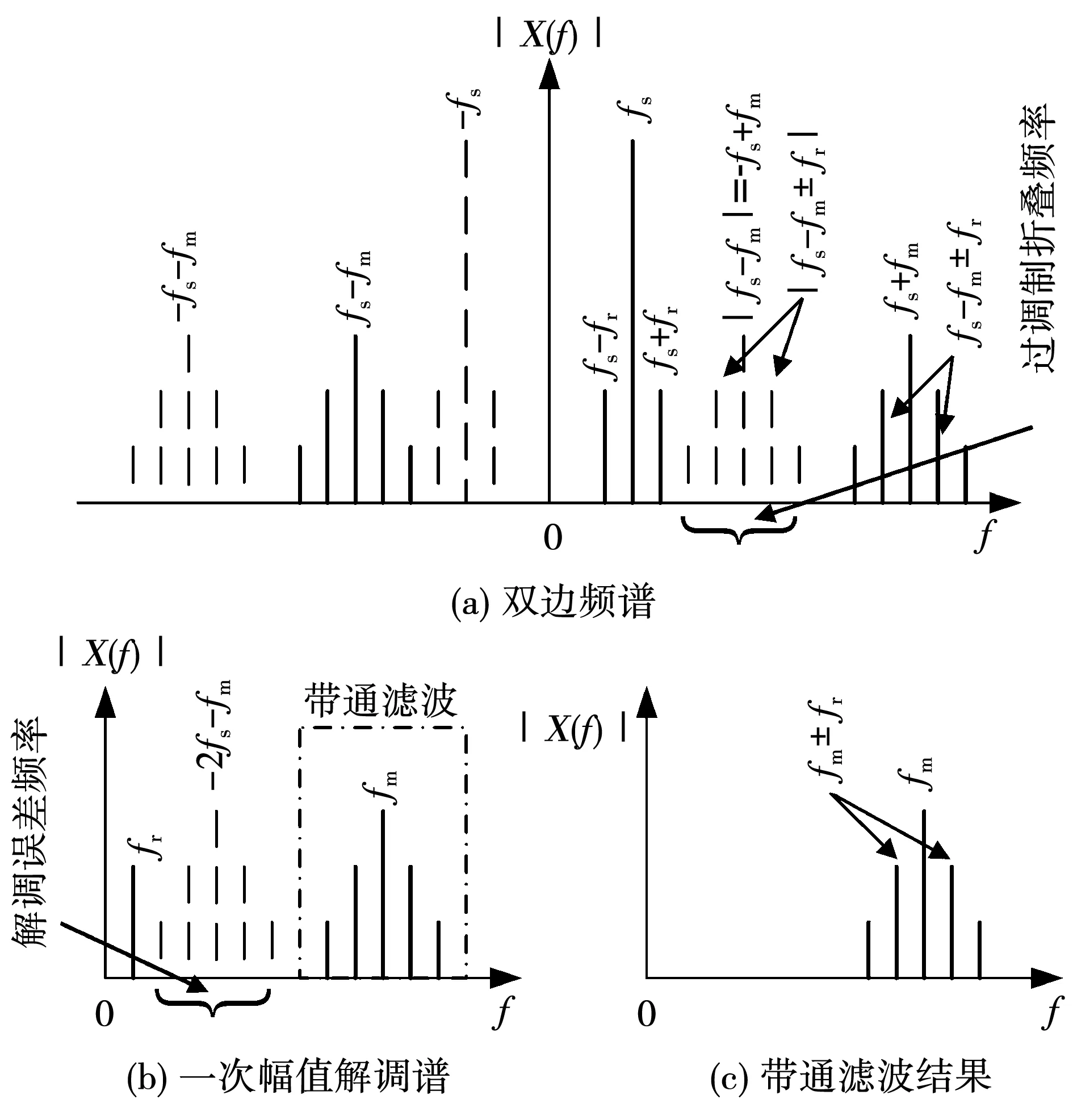
圖4 齒輪的定子電流信號雙邊頻譜示意圖Fig.4 Schematic diagram of bilateral spectrum of gear stator current signal

3 二次幅值解調(diào)分析算法

3.1 基本原理

設(shè)x(t)為一個實信號，其Hilbert變換定義為

(7)

由原始信號x(t)和它的Hilbert變換信號h(t)可以構(gòu)成一個新的解析信號：

xa(t)=x(t)+jh(t)，

(8)

其模

(9)

即為原始信號x(t)的幅值解調(diào)(包絡(luò))信號。

3.2 采用Hilbert變換的幅值解調(diào)計算流程

由于1/(πt)的傅立葉變換為符號函數(shù)，根據(jù)傅立葉變換的卷積性質(zhì)，式(7)右端的卷積關(guān)系在頻域中變?yōu)槌朔e關(guān)系：

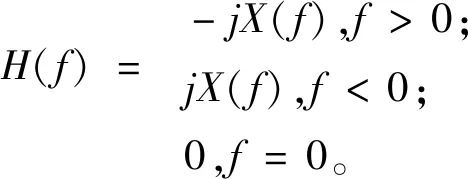
(10)

這相當(dāng)于對時域信號x(t)進(jìn)行90°移相處理，可以借助FFT(fast fourier transform，F(xiàn)FT)和逆FFT變換在頻域內(nèi)完成，然后再根據(jù)式(9)即可求得原始信號的包絡(luò)信號。一個完整的數(shù)字信號x(n)的Hilbert包絡(luò)信號|xa(n)|求解流程如圖5所示。

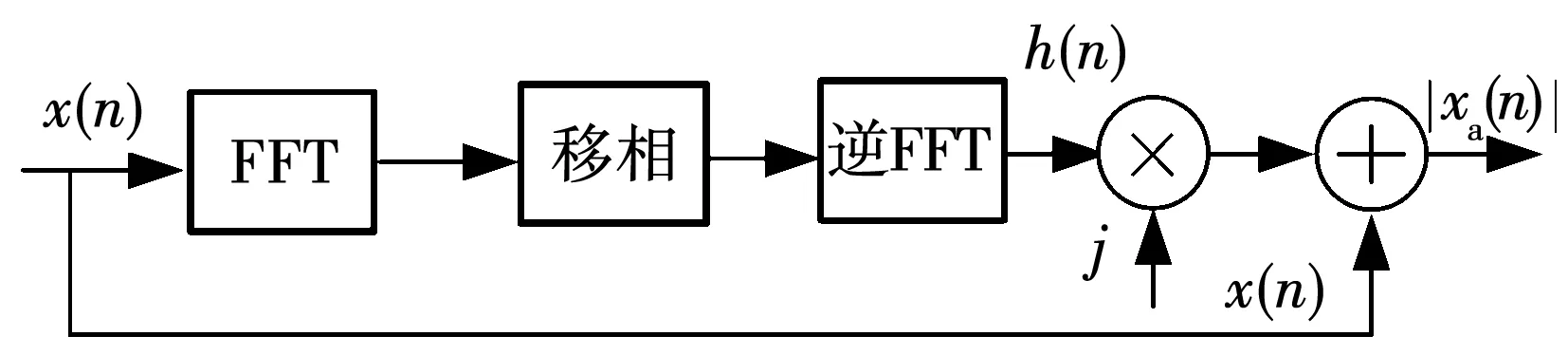
圖5 Hilbert變換幅值解調(diào)(包絡(luò))求解流程Fig.5 Hilbert transform amplitude demodulation (envelope)solution process

3.3 定子電流信號的二次幅值解調(diào)譜算法流程

將圖5所示的Hilbert變換幅值解調(diào)過程執(zhí)行兩次并做FFT頻譜分析，可以得到二次幅值解調(diào)(或稱二次包絡(luò))譜，具體計算流程見圖6所示。

圖6 Hilbert變換求解二次幅值解調(diào)(包絡(luò))譜流程Fig.6 Hilbert transform for solving quadratic amplitude demodulation(envelope)spectrum process

4 交流電動機(jī)驅(qū)動齒輪系統(tǒng)仿真模型

交流異步電機(jī)驅(qū)動齒輪傳動系統(tǒng)的仿真模型如圖7所示。仿真模型包括異步電動機(jī)模塊及PWM變頻電源模塊、電參數(shù)測量模塊和齒輪故障模擬模塊等組成，各模塊均直接采用MATLAB/Simulink仿真庫提供的元件。為了減少PWM變頻模塊的諧波干擾，在電動機(jī)的供電一側(cè)增加了LC濾波模塊。為了減少采樣誤差，在電機(jī)綜合測量模塊后添加了截止頻率為1 500 Hz的模擬低通濾波器，然后接示波器模塊采集、存儲定子電流信號進(jìn)行分析。

電動機(jī)額定功率1.5 kW，380 VAC，50 Hz，極對數(shù)為3，系統(tǒng)折算到電動機(jī)的總轉(zhuǎn)動慣量為0.07 kg·m2，其它仿真參數(shù)略。當(dāng)大齒輪發(fā)生故障(如齒面局部剝落)時，會產(chǎn)生額外的沖擊力矩，此時，可以參照式(5)和圖3構(gòu)造沖擊力矩函數(shù)TF，加上恒定的負(fù)載力矩(Constant torque 2)5 N·m，接入電機(jī)模塊的Tm輸入端即可。需要注意的是，為了仿真參數(shù)設(shè)定方便，圖7中的變形量值(如δmin)實際為參照式(3)計算后的結(jié)果。

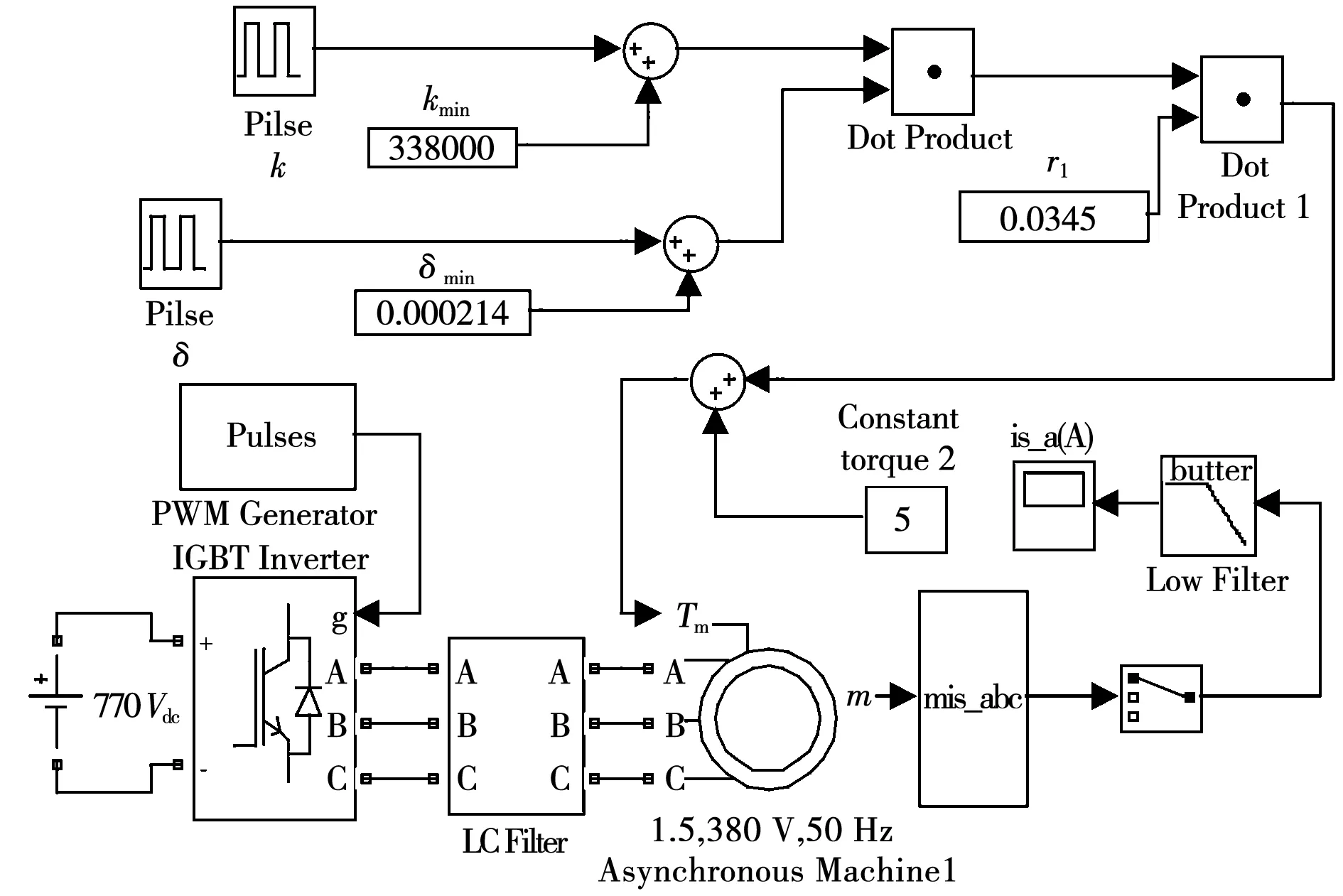
圖7 電動機(jī)驅(qū)動齒輪故障模擬仿真模型Fig.7 Failure simulation model of motor drive gear

5 齒輪故障模擬試驗臺

齒輪傳動系統(tǒng)故障模擬試驗臺以及控制和數(shù)據(jù)采集系統(tǒng)示意如圖8所示，試驗臺實體照片如圖9所示。試驗臺主要由驅(qū)動電動機(jī)及配套變頻調(diào)速系統(tǒng)、齒輪傳動系統(tǒng)、模擬負(fù)載發(fā)電機(jī)及其勵磁系統(tǒng)構(gòu)成。其中驅(qū)動電動機(jī)為1.5 kW三相交流異步電動機(jī)，配備變頻器調(diào)節(jié)轉(zhuǎn)速；傳動系統(tǒng)由減速齒輪傳動副組成；模擬負(fù)載系統(tǒng)由三相雙饋感應(yīng)發(fā)電機(jī)(doubly fed induction generator，DFIG)配合三相阻性負(fù)載組成，其中DFIG由1.5 kW繞線式三相異步電動機(jī)代替，發(fā)電機(jī)的定子線圈與Y型接法的三相阻性負(fù)載(白熾燈)連接，通過更換不同功率的白熾燈模擬負(fù)載變化。發(fā)電機(jī)轉(zhuǎn)子線圈與勵磁變頻器相連，根據(jù)驅(qū)動電動機(jī)的頻率設(shè)定值，改變發(fā)動機(jī)轉(zhuǎn)子勵磁頻率的大小，以保證發(fā)電機(jī)輸出頻率恒定為50 Hz。

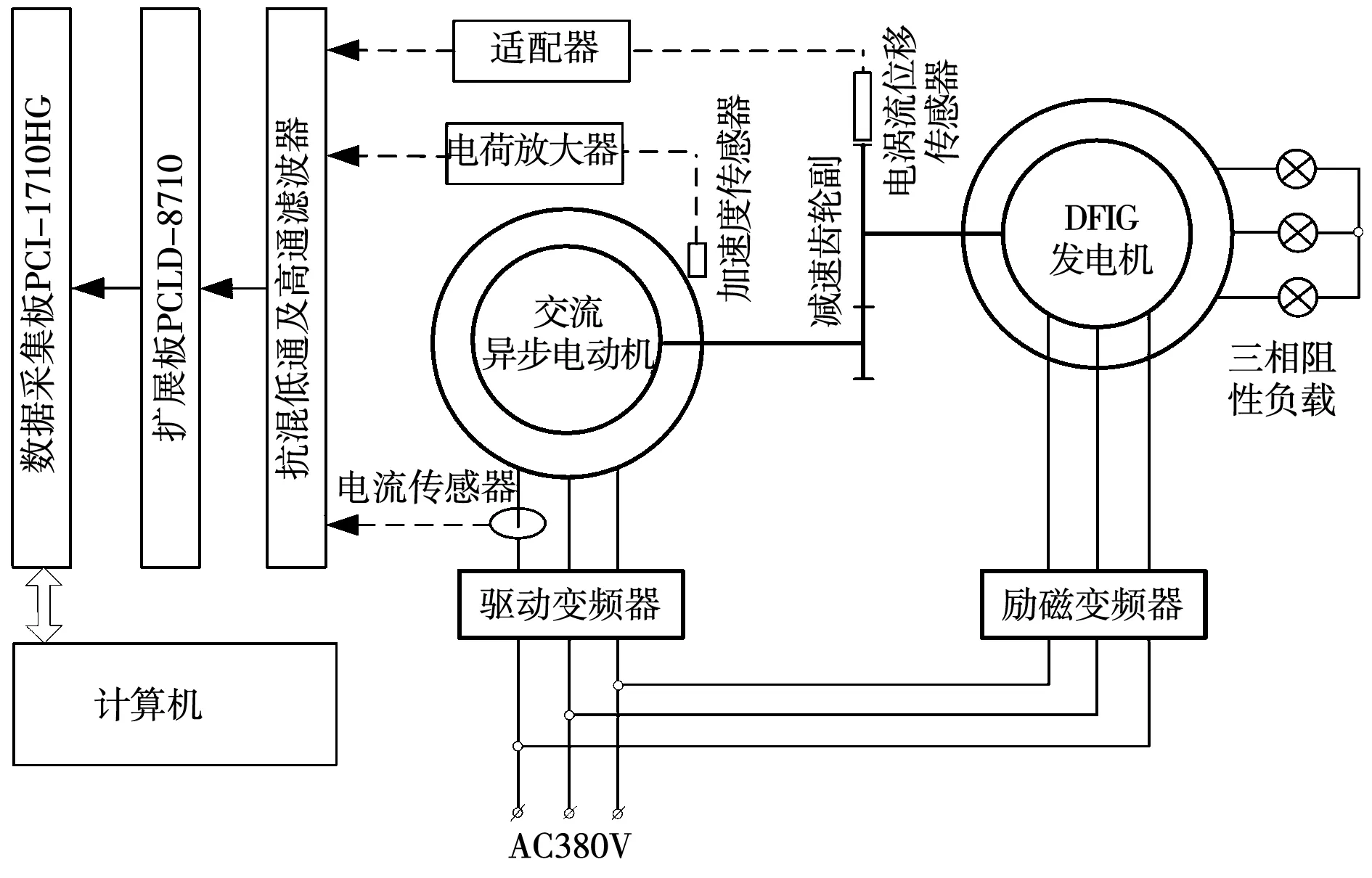
圖8 齒輪故障模擬試驗臺組成示意圖Fig.8 Schematic diagram of gear fault simulation test bench

圖9 齒輪故障模擬試驗臺Fig.9 Gearfault simulation test bench

為了減少傳動系統(tǒng)其它部件的干擾，采用最簡單的單級齒輪對模擬減速齒輪箱，齒輪采用開放式安裝，潤滑脂潤滑，其中電動機(jī)側(cè)小齒輪的齒數(shù)為z1=23，發(fā)電機(jī)側(cè)大齒輪的齒數(shù)z2=34，減速比約為1.478。采用氬弧焊溶化大齒輪的一個輪齒的部分齒面，模擬齒面磨損或疲勞剝落故障(如圖10(b)所示)。

圖10 試驗用齒輪示意圖Fig.10 Test gear diagram

采用KLC型鉗形儀用電流互感器獲取電動機(jī)變頻器后的定子電信號并進(jìn)行分析。安裝在大齒輪側(cè)面的電渦流位移傳感器用于測量大齒輪的轉(zhuǎn)速信號；電動機(jī)端蓋上安裝的加速度傳感器用于測取齒輪的振動加速度信號，并與定子電流信號進(jìn)行比較分析。

6 計算機(jī)模擬仿真結(jié)果及分析

首先利用圖7所示的仿真模型進(jìn)行Simulink仿真分析。其中示波器模塊的穩(wěn)態(tài)信號采樣頻率為5120 Hz，點數(shù)為1048576點，利用MATLAB進(jìn)行幅值譜、以及一次和二次包絡(luò)譜分析。為了頻譜圖表示清楚起見，頻率顯示范圍為0～200 Hz或0～100 Hz。

6.1 齒輪正常時的仿真結(jié)果

當(dāng)圖7中的故障模擬方波函數(shù)Pulse δ幅值為0時，相當(dāng)于電動機(jī)的機(jī)械轉(zhuǎn)矩Tm中僅包含齒輪嚙合頻率成分，即齒輪處于正常狀態(tài)。仿真時，PWM輸出頻率fs設(shè)定為15 Hz，嚙合頻率fm為113.3 Hz，此時的定子電流信號分析結(jié)果(單邊頻譜)如圖11所示。從幅值譜(圖11(a))中可以看出15 Hz的主電源頻率成分，以及嚙合頻率產(chǎn)生的兩個邊帶成分為128.3 Hz (128.3=|fs+fm|=15+113.3)和98.33 Hz(98.33≈|fs-fm|=|15-113.3|)，顯然，根據(jù)前面的分析，98.33 Hz為過調(diào)制折疊頻率。

對該信號直接做Hilbert幅值解調(diào)分析，可得一次包絡(luò)譜如圖11(b)所示。發(fā)現(xiàn)除了嚙合頻率fm=113.3 Hz之外，還有一個83.33 Hz的未知解調(diào)成分，其等于98.33-15 Hz，這就是過調(diào)制折疊頻率產(chǎn)生的解調(diào)誤差頻率。

如果對該信號再做一次Hilbert幅值解調(diào)分析，可得二次包絡(luò)譜如圖11(c)所示，可見雖然去除了嚙合頻率成分以及過調(diào)制現(xiàn)象時出現(xiàn)的誤差頻率成分，但仍然殘留了兩個過調(diào)制邊帶信號的差頻30 Hz(≈113.3-83.33)成分。

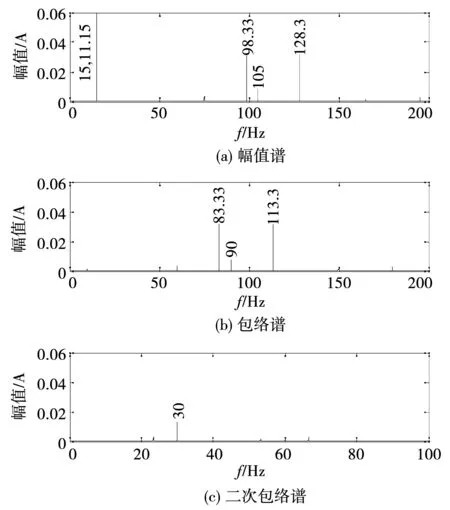
圖11 齒輪正常時的仿真定子電流信號頻譜Fig.11 Simulated stator current signal spectrum when the gear is normal

6.2 齒輪齒面局部故障時的仿真結(jié)果

故障仿真時，變頻器設(shè)定頻率fs仍為15 Hz，嚙合頻率為113.3 Hz，模擬齒輪局部故障的方波函數(shù)Pulse δ的幅值δmax=0.01 mm，頻率為3.33 Hz。此時的定子電流信號幅值譜(圖12(a))出現(xiàn)了大量的諧波和邊帶成分，且這些邊帶與嚙合頻率載波成分(128.3和98.33 Hz)并不成幅值對稱分布。根據(jù)理想時的過調(diào)制信號(圖4)特征分析，可知這是由于多階邊帶之間相互交叉或疊加的結(jié)果。

顯然，利用這種頻譜直接進(jìn)行故障診斷是非常困難的，此時可以采用二次包絡(luò)譜分析方法，計算結(jié)果如圖12(c)所示。我們先觀察圖12(b)所示的一次包絡(luò)譜，可見已經(jīng)剔除了電源頻率的15 Hz成分，但是嚙合頻率113.3 Hz及其調(diào)制邊帶依然存在。另外，雖然一次包絡(luò)譜已經(jīng)解調(diào)出了3.34 Hz的齒輪故障頻率，但是，其一倍頻成分的幅值甚至不如3倍頻的幅值大，這種頻譜分布形式顯然不合常理。再來看一下二次包絡(luò)譜(圖12(c))，可以發(fā)現(xiàn)又去除了嚙合頻率成分和83.33 Hz的過調(diào)制成分，僅將3.34 Hz及倍頻的齒輪故障頻率解調(diào)出來，而且故障特征頻率的幅值分布也符合諧波階數(shù)越高，幅值越低的一般規(guī)律。

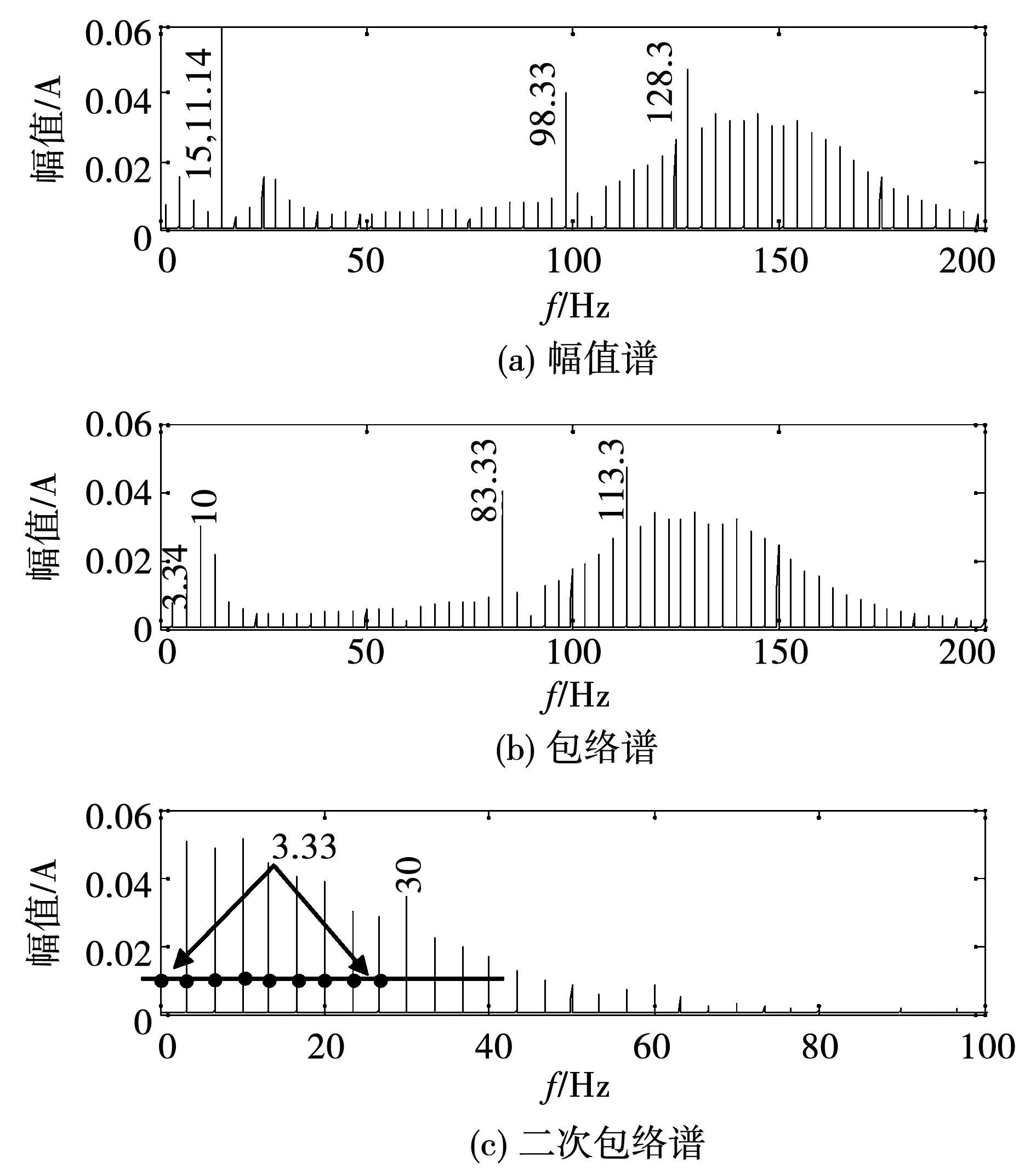
圖12 齒輪故障時的仿真定子電流信號頻譜Fig.12 Spectrum of simulated stator current signal in the case of gear failure

比較齒輪正常時和故障時的二次包絡(luò)譜，可見兩者差別顯著，說明二次包絡(luò)分析對定子電流信號十分有效。可以剔除電源頻率成分及齒輪嚙合頻率調(diào)制成分，得到的頻譜成分僅包含3.33 Hz的齒輪故障調(diào)制成分及多階倍頻成分，且頻譜成分單一，幅值分布合理，便于特征識別與故障診斷。

7 試驗臺試驗結(jié)果及分析

利用圖8和圖9所示的齒輪故障模擬試驗臺，針對齒輪正常(圖10(a))和齒面局部故障(圖10(b))兩種情況分別進(jìn)行試驗分析。試驗時發(fā)電機(jī)轉(zhuǎn)子勵磁頻率設(shè)為38.5 Hz，三相總負(fù)載為120 W，電動機(jī)變頻器設(shè)定頻率為15 Hz。定子電流信號采樣前經(jīng)1 500 Hz的抗混低通濾波處理，采樣頻率為5 120 Hz，點數(shù)為1 048 576點。

7.1 齒輪正常時的試驗結(jié)果分析

齒輪正常時的定子電流分析結(jié)果如圖13所示，其中幅值譜(圖13(a))中可以看到電源頻率14.99 Hz及2倍頻(29.99 Hz)成分以及5、7倍頻成分(74.96、104.9 Hz)等。另外，還有128.7 Hz和98.7 Hz的嚙合頻率調(diào)制成分。在圖13(b)所示的一次包絡(luò)譜中也可以發(fā)現(xiàn)電源頻率及其倍頻成分,這些都是將電源頻率與倍頻成分之差作為解調(diào)成分時的解調(diào)結(jié)果。另外，還有嚙合頻率成分(113.7 Hz)，以及過調(diào)制誤差解調(diào)頻率(83.7 Hz)等。但是，經(jīng)二次包絡(luò)解調(diào)處理的頻譜(圖13(c))中并沒有幅值較為顯著的頻率成分，說明齒輪處于正常狀態(tài)。

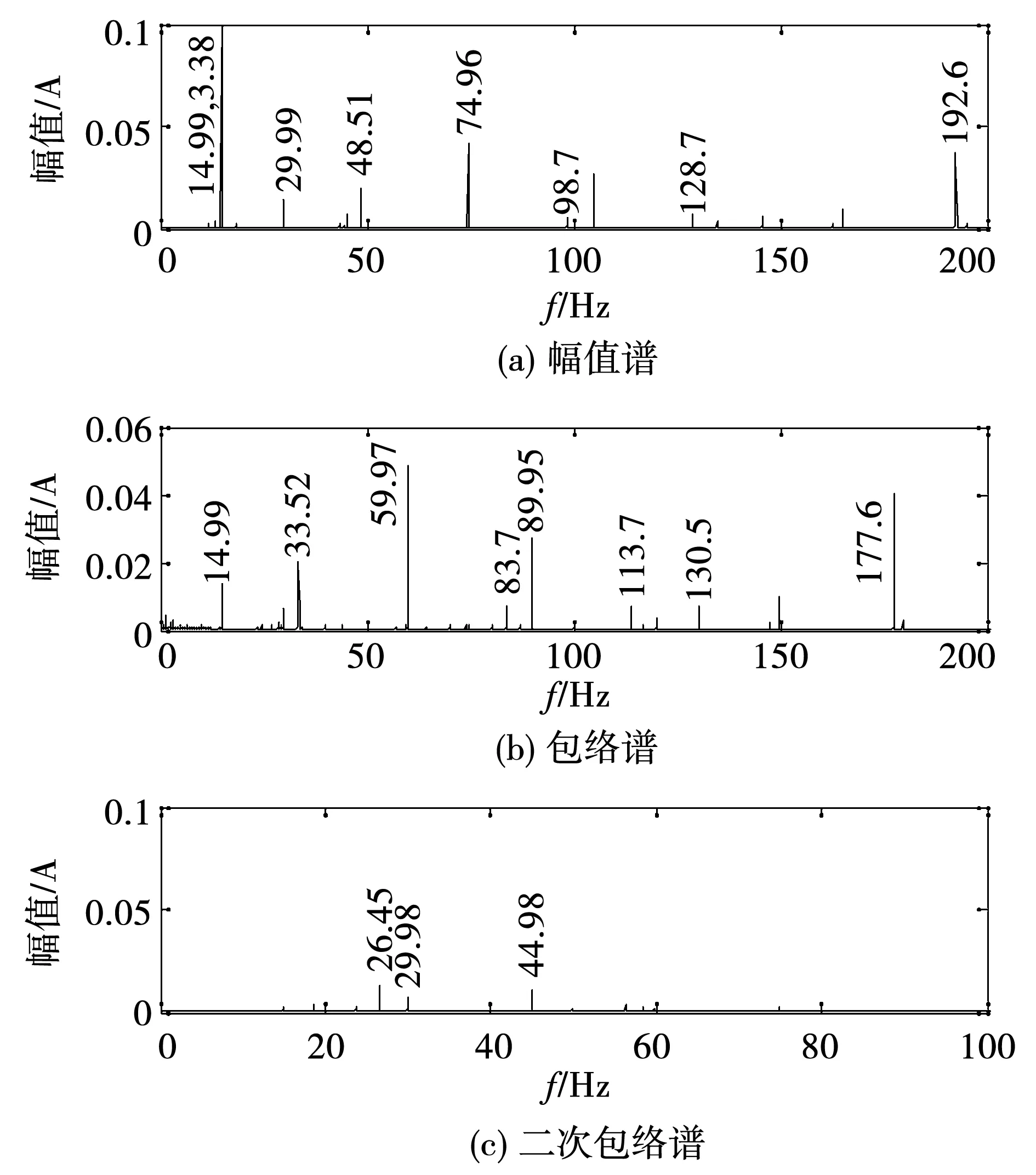
圖13 試驗齒輪正常時的定子電流信號頻譜Fig.13 Frequency spectrum of stator current signal whenthe test gear is normal

7.2 齒輪齒面局部故障時的試驗結(jié)果分析

大齒輪齒面存在局部故障時的定子電流信號分析結(jié)果如圖14所示。其中幅值譜(圖14(a))的頻譜特征分布與齒輪故障時的仿真結(jié)果(圖12(a))很相似，同樣出現(xiàn)了豐富的等間隔(3.34 Hz)邊帶成分。根據(jù)前面的理論分析，這些邊帶會互相抵消或疊加，造成邊帶成分的不均勻分布與偏移。例如，從圖14 (b)中的一次包絡(luò)譜中的擴(kuò)大部分小窗口可以看出，真正的故障頻率3.34 Hz成分被未知的3.25 Hz和3.44 Hz成分遮擋住了，從而造成了故障特征頻率定位不準(zhǔn)確。

齒輪故障時的定子電流信號二次包絡(luò)譜分析結(jié)果如圖14 (c)所示。圖中僅存大齒輪轉(zhuǎn)頻3.34 Hz及倍頻成分，并且幅值分布形式符合隨倍頻頻率增長而逐漸下降的一般頻譜分布規(guī)律，而且與正常時的二次包絡(luò)譜 (圖13(c))相比差別顯著，意味著大齒輪出現(xiàn)了故障。

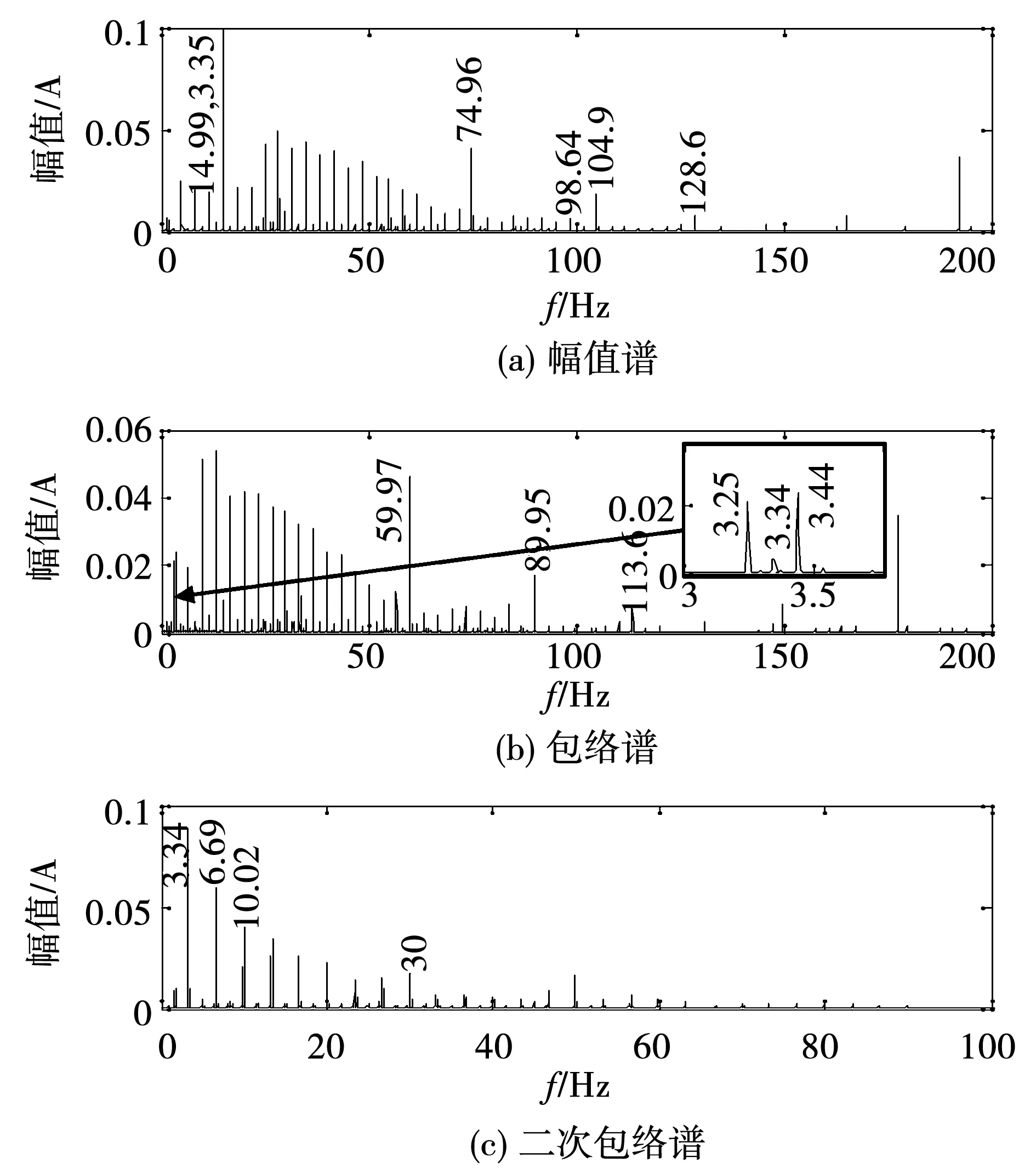
圖14 試驗齒輪故障時的定子電流信號頻譜Fig.14 Frequency spectrum of stator current signal when the test gear fault

7.3 齒輪振動位移信號和加速度信號試驗結(jié)果比較

限于篇幅，僅給出了齒輪故障時的大齒輪側(cè)安裝的電渦流位移傳感器位移信號，以及齒輪振動加速度信號的幅值譜及一次包絡(luò)譜分析結(jié)果，如圖15和圖16所示。位移信號和加速度信號的采樣頻率均為5 000 Hz，采樣點數(shù)為1 048 576，信號采樣前經(jīng)1 500 Hz的低通濾波處理。

從圖15的齒輪位移信號幅值譜(圖14(a))可以看出大齒輪的齒通過頻率為113.7 Hz，對應(yīng)圖13中的一次包絡(luò)譜中的齒輪嚙合頻率113.7 Hz，或幅值譜中的128.7 Hz調(diào)制成分。從圖16的振動信號幅值譜也可以看出這個頻率成分，但頻率定位精確度明顯不足，約為115.2 Hz。

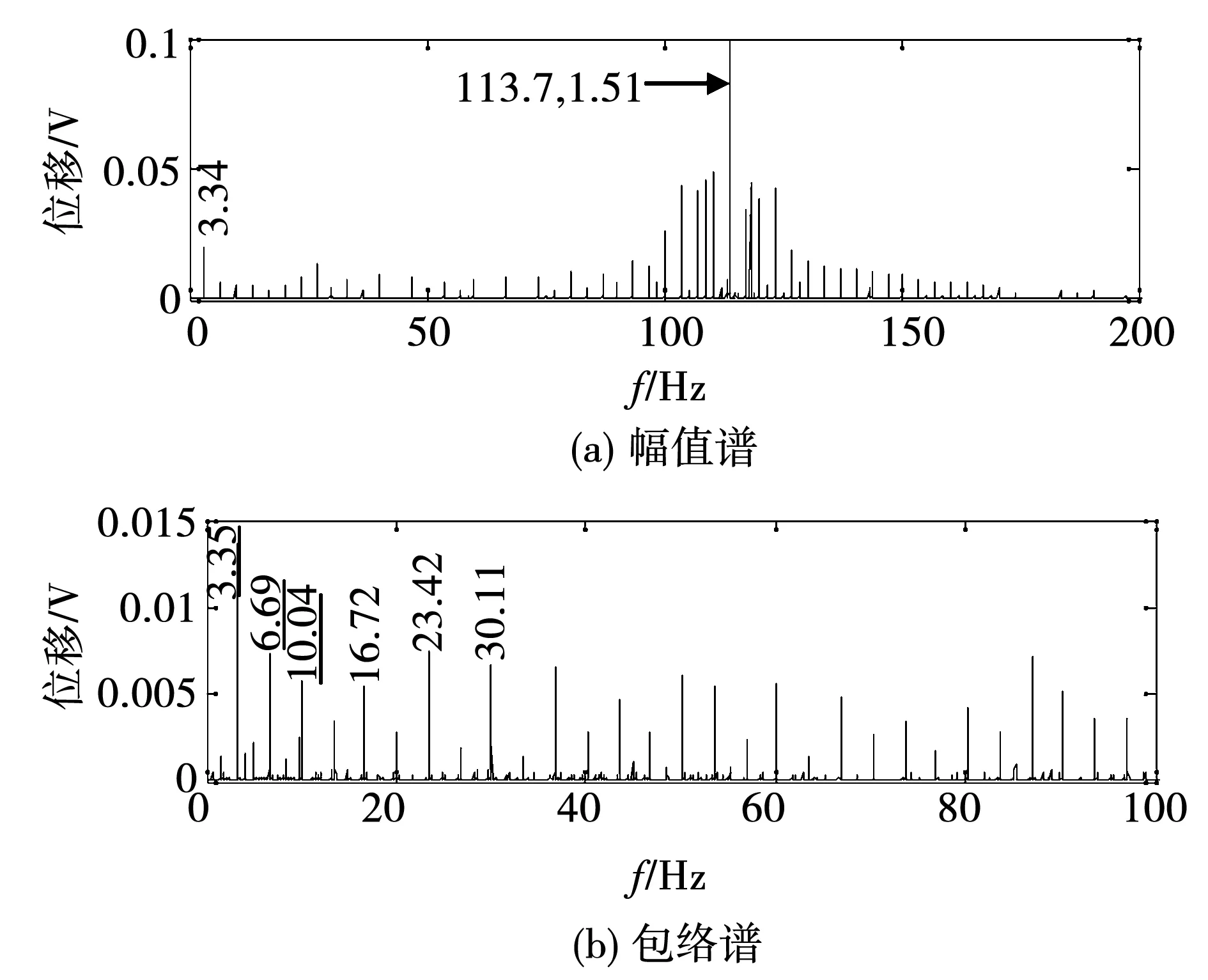
圖15 試驗齒輪故障時的齒輪振動位移信號頻譜Fig.15 Frequency spectrum of gear vibration displacement signal when the test gear fault

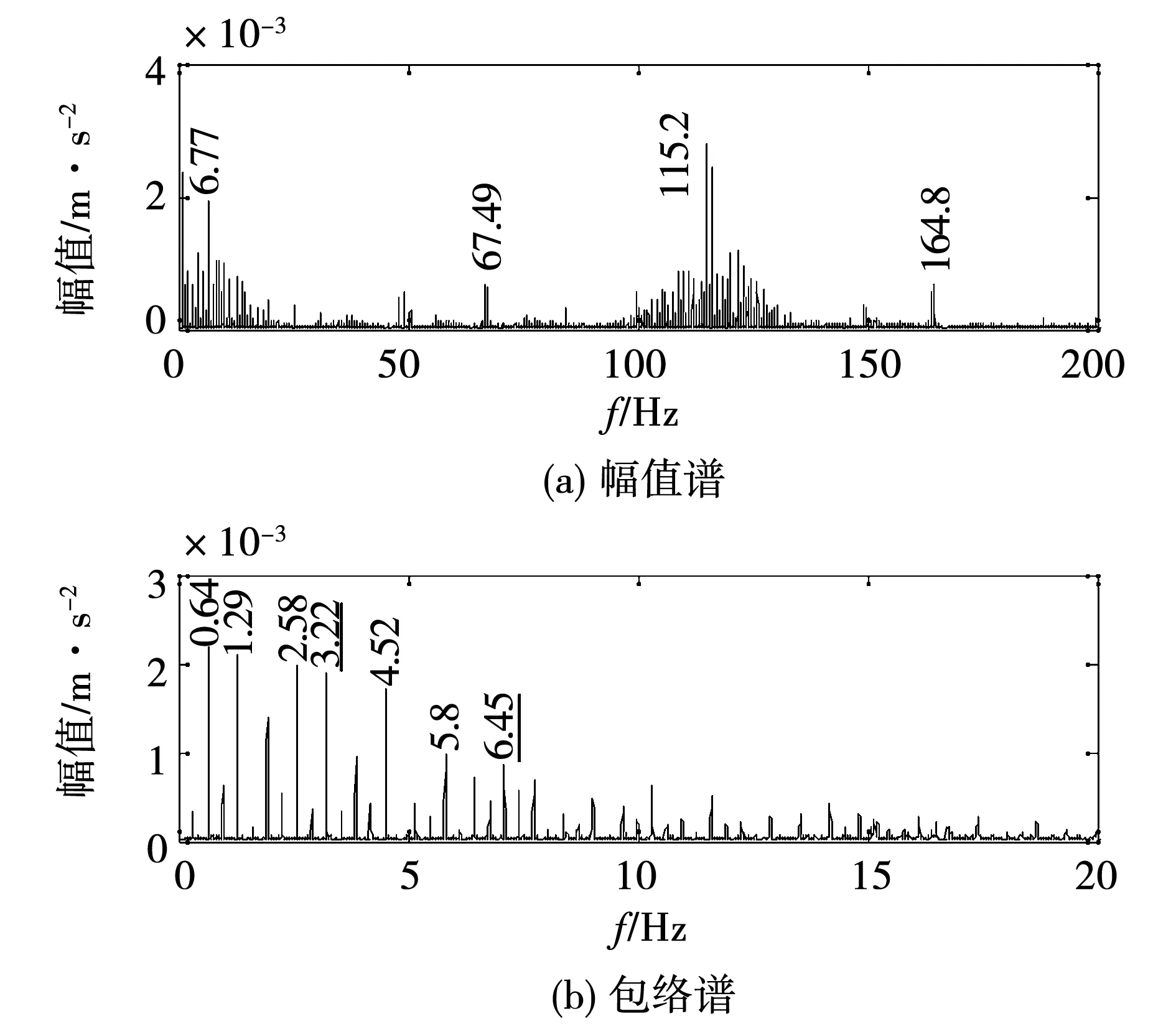
圖16 試驗齒輪故障時的振動加速度信號頻譜Fig.16 Frequency spectrum of vibration acceleration signal when the test gear fault

實際上，這種齒輪測速裝置還可以起到類似齒盤測扭振的作用[18]，此時只需對電渦流傳感器位移信號進(jìn)行解調(diào)分析即可。分析前需要以嚙合頻率為中心進(jìn)行帶通濾波處理，以去除低頻段的干擾成分。幅值解調(diào)分析結(jié)果如圖15 (b)所示，從中可以發(fā)現(xiàn)和定子電流信號分析結(jié)果(圖14(c))接近的多階故障調(diào)制成分，如3.35、6.69和10.04 Hz等(為了表示它們之間的倍頻關(guān)系，圖中的這些頻率標(biāo)注加了下劃線)。

在以嚙合頻率為中心進(jìn)行帶通濾波并解調(diào)后的振動加速度信號包絡(luò)譜(圖16(b))中，也可以發(fā)現(xiàn)齒輪的故障調(diào)制3.22 Hz及倍頻6.45 Hz等。與定子電流信號分析結(jié)果(圖14(c))相比，雖然加速度信號頻率定位準(zhǔn)確度不足，但是齒輪故障調(diào)制頻率及其倍頻的幅值分布形式與電流信號還是基本一致的，這些都說明了定子電流信號分析結(jié)果的正確性和準(zhǔn)確性。

另外，振動加速度信號還包含了很多電流信號并不存在的頻率成分，如0.64 Hz和1.92 Hz成分等，說明振動加速度信號的靈敏度高，但是這也同時增加了振動信號頻譜識別難度。而電流信號中的故障頻率成分單一，易于識別，故障診斷的魯棒性好，這是MCSA方法的主要優(yōu)點之一。

8 結(jié) 論

1)理論分析、仿真與試驗表明：在“過調(diào)制”狀態(tài)下，齒輪嚙合頻率及其邊帶會在定子電流信號幅值譜中產(chǎn)生過調(diào)制折疊頻率簇。當(dāng)直接進(jìn)行幅值解調(diào)分析時，過調(diào)制折疊頻率除了會產(chǎn)生額外的過調(diào)制誤差頻率成分外，還可能與正常的調(diào)制頻率成分交叉、疊加，造成頻譜成分復(fù)雜，故障特征不易識別。

2)本文將故障引起的齒面誤差作為彈性變形量，估計故障齒輪嚙合時產(chǎn)生的激振力矩，仿真時具有故障激勵信號連續(xù)、生成方便的優(yōu)點，而且計算機(jī)仿真與理論分析和試驗臺模擬試驗結(jié)果的頻譜分布形式高度吻合，充分證明了該計算模型的正確性和準(zhǔn)確性。

3)二次幅值解調(diào)(包絡(luò))分析方法簡便易行，可以有效剔除定子電流信號中的電源及齒輪嚙合頻率成分，消除過調(diào)制現(xiàn)象引起的頻率混疊誤差，得到的齒輪故障頻率成分更加準(zhǔn)確與清晰，且諧波幅值分布也符合常見的齒輪故障特征分布規(guī)律。

目前，本方法尚存在一些問題，如二次解調(diào)譜仍然遺留有兩個過調(diào)制邊帶頻率之差頻，但實際幅值不大，對整體分析結(jié)果影響較小。