大飛機空速異常輔助決策功能空速構建方法研究

吳佳駒，蘇幸君，朱妍

（1.航空工業第一飛機設計研究院總體設計研究所，西安710089）

（2.中國飛行試驗研究院技術中心航電所，西安710089）

0 引 言

空速是飛行員重點關注的飛行參數之一，空速異常通常會引起較為嚴重的飛行事故，并且難以通過地面檢查完全排除該故障。自20世紀90年代以來，因空速異常引發的大飛機事故多達十數起，輕則導致飛機返航，重則導致飛機墜毀。

當空速異常發生時，主要依賴飛行員進行危險狀態改出操作，然而空速異常多伴隨著相關系統的異常，短時間內會觸發大量告警信號，致使飛行員工作負荷劇增；同時，在復雜且多變的飛行環境下，受到人體生理和心理承受能力的限制，飛行員決策的正確性也將受到影響。

國外主要在傳感器正常狀態下，開展了空速氣動補償方法研究，以獲取更準確的修正空速值。國內主要在飛機過失速狀態下，開展了大氣數據融合方法研究，以提供可靠的大氣參數狀態反饋。

國內外針對傳感器故障時的飛行員輔助方法研究較少。因此，本文設計大飛機空速異常輔助決策功能空速構建方法，在空速異常時，將協助飛行員完成快速正確地操縱，提高飛機的生存率。

1 空速異常輔助決策功能

1.1 功能定義

當飛機發生空速異常時，電子化顯示操縱流程，綜合利用機載系統狀態信號和傳感器信號，輔助飛行員進行異常信號判斷，并給出安全飛行操縱提示，保障飛行安全。

1.2 功能原理

大飛機空速異常輔助決策功能包括人機交互界面設計和空速構建方法研究，功能原理如圖1所示。本文重點研究空速構建方法。

圖1 空速異常輔助決策功能原理Fig.1 Principle of airspeed anomalies auxiliary decision-making function

人機交互界面設計：基于快速檢查單的內容和重構的空速，以電子條目化的形式顯示由飛行員確認的輔助內容，供飛行員在緊張時間壓力下快速參考，完成故障改出操縱，界面如圖2所示。

圖2 電子條目化界面設計Fig.2 Design of electronic itemization display

空速構建方法研究：基于不同的飛行階段和飛機性能，通過升力方程、風速重構、飛行狀態符合性判斷方法，確定當前真實的空速，輔助飛行員操縱。

2 空速構建方法

飛機指示空速來自大氣數據系統，一般情況下，大飛機配備三套大氣數據系統：一套將數據給主駕送顯，一套給副駕送顯，還有一套作為備份。

以三套大氣系統為例，傳感器故障包括非共模故障和共模故障兩類。當發生非共模故障時，傳感器的信號值一致；當發生共模故障時，傳感器的信號值一致，余度表決無法識別。

空速信號的綜合判斷流程如圖3所示。

圖3 信號綜合判斷流程Fig.3 Comprehensive judgment process of signals

當大飛機處于非巡航平飛狀態，對采集的空速信號進行余度表決，判斷信號的正確性。如果信號正確，則三套大氣數據系統工作正常，繼續使用機長側的空速值作為當前的真實空速；如果信號故障，在相對低的速度的飛行包線中，采用升力方程重構空速，否則采用風速重構空速。

當三套大氣傳感器發生共模故障，余度表決方法將無法識別故障，左側算法將采用機長側的錯誤空速值，引發飛行安全問題。針對該情況，在大飛機巡航平飛狀態時，無論故障是否為共模故障，均可通過飛行狀態符合性方法識別故障信號，給出真實空速，輔助飛行員完成危險狀態改出。

升力方程、風速重構、飛行狀態符合性等空速構建方法將在下文進行詳述。

2.1 余度表決

以大運飛機為例，將三套大氣機解算的空速信號按由大到小的順序排隊，通過兩兩信號的差值判斷信號狀態，可能的狀態如表1所示。

表1 空速信號余度表決Table 1 Airspeed signal redundancy voting

當傳感器設備出現非共模故障時，通過余度表決，可以判斷信號是否正確。當傳感器設備出現共模故障時，三套大氣機的數值會出現同等突變，余度表決將無法識別出故障數值。此時，如果飛機處于巡航平飛狀態時，將自動通過2.4節的“飛行狀態符合性判斷”方法識別出真實的空速。

2.2 基于升力方程重構空速

由于空速管暴露在外部環境中，并且會被能夠部分或全部堵塞傳感器的物質干擾，產生錯誤的壓力測量值，開發獨立于空速管估計空速的替代方法是有必要的。

（1）升力方程原理

在相對低的速度的飛行包線中，使用升力方程較為準確。升力方程與垂直負載因素、迎角、質量和速度參數有關，通過迎角、垂直負載因素和質量可以重構實時的等效速度。升力方程的公式為

式中：

n

為垂直負載因數；

m

為飛機的質量；

g

為重力加速度；

S

為參考面積；

C

為升力的氣動力系數的梯度；

α

為迎角；

α

為零升力迎角；

q

為動壓。

式中：

ρ

為空氣密度；

v

為飛行速度（真空速）。

聯立式（1）~式（2），可得空速為

空氣密度為

式中：

P

為當地大氣壓；

P

為標準物理氣壓；

T

為實際絕對溫度。

式中：

T

為攝氏溫度。

式中：

T

為

H

點的攝氏溫度；

T

為對流層參考點的溫度；

H

為與參考點的相對高度差。

當地大氣壓為

式中：

H

為氣壓高度。

輸入信號及其來源如表2所示。

表2 輸入信號及其來源Table 2 Input signals and their sources

在相對低的速度飛行時，在適當的迎角范圍內，大飛機的升力系數與迎角基本呈線性關系。本文將使用最小二乘法進行升力系數的曲線擬合，算法原理為：

設 (

x

，

y

)是 一 對 觀 測 量 ，且

x

=[

x

，

x

，…，

x

]∈

R

，滿足以下理論函數：

為了尋找函數

f

(

x

，

w

)的參數

w

的最優估計值，對于給定

m

組（通常

m

>

n

）觀測數據(

x

，

y

)(

i

=1，2，…，

m

)，求解目標函數

取最小值的參數

w

(

i

=1，2，…，

m

)。

對于無約束最優化問題，最小二乘法的一般形式為

式中：

L

(

x

)(

i

=1，2，…，

m

)，為殘差函數。

對于未定型的大飛機，在典型的馬赫數和典型的迎角下，進行風洞試驗，得到典型狀態點的升力系數，并對試驗得到的升力系數進行曲線擬合，從而得到迎角、馬赫數全包線下的升力系數。通過實時計算升力系數，可代替飛行員手動查閱性能手冊。對于已定型的大飛機，性能數據準確、充實，可直接選取升力系數進行計算。

以大運飛機為例，當速度為0.2

Ma

時，基于15組不同迎角下的升力系數值，使用最小二乘法依次進行1~9次的曲線擬合，如圖4所示，可以看出：在相對低的速度飛行時，大飛機的升力系數與迎角近似為線性關系。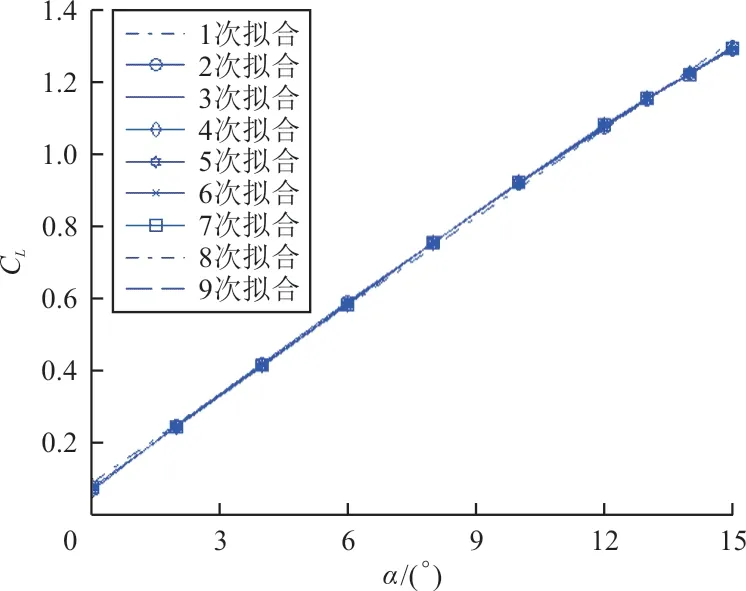

圖4 大飛機升力系數的曲線擬合Fig.4 Curve fitting of lift coefficient of large aircraft

（2）仿真驗證

在面積

S

=486 m，

g

=9.81 m/s下，選取5組典型點，進行算法可靠性驗證。例1，取配平點1的狀態參數為：

m

=143 000 kg，

H

=1000 m，

α

=13.133 9°。

計算得升力系數為1.159 7，空氣密度為1.077 kg/m，飛行速度為66.31 m/s。通過升力方程計算的平衡點速度為67.28 m/s，誤差值0.97 m/s，誤差百分比1.44%。

例2，取配平點2的狀態參數為：

m

=143 000 kg，

H

=1000 m，

α

=5.225 0°。

計算得升力系數為0.520 4，空氣密度為1.077 kg/m，飛行速度為101.49 m/s，平衡點速度為100.92 m/s，誤 差 值0.57 m/s，誤 差 百 分 比0.56%。

例3，取配平點3的狀態參數為：

m

=160 000 kg，

H

=1 000 m，

α

=14.973 7°。

計算得升力系數為1.281 8，空氣密度為1.077 kg/m，飛行速度為68.40 m/s，平衡點速度為67.28 m/s，誤差值1.12 m/s，誤差百分比1.66%。

例4，取配平點4的狀態參數為：

m

=143 000 kg，

H

=3 000 m，

α

=6.929 9°。

計算得升力系數為0.662 8，空氣密度為0.879 kg/m，飛行速度為99.57 m/s，平衡點速度為98.58 m/s，誤差值0.99 m/s，誤差百分比1.01%。

例5，取配平點5的狀態參數為：

m

=143 000 kg，

H

=8 000 m，

α

=0.942 1°。

計算得升力系數為0.162 8，空氣密度為0.560 kg/m，飛行速度為251.60 m/s，平衡點速度為242.09 m/s，誤 差 值9.51m/s，誤 差 百 分 比3.93%。

由仿真結果可知，通過升力方程重構的馬赫數，在大飛機0.8

Ma

速度內，可用于空速的重構，結果較為準確。

2.3 基于風速重構空速

在相對高的速度的飛行包線中，升力方程將不準確。此時，需通過風速重構空速，算法原理如圖5所示。

圖5 通過風速重構空速原理Fig.5 Principle of airspeed reconstruction through wind speed

當空速正常時，通過地速和真空速實時計算風速，存入風速數據庫；當空速異常時，由于風速傳感器可能出現故障，需要判斷風速傳感器的信號是否正確。基于經驗選取風速數據庫中近八拍的風速平均值，與當前風速傳感器值進行對比，若誤差小于風速平均值的5%，則傳感器正常，可以使用風速傳感器值。

由風速和故障時刻的地速計算真空速，結合當前飛行高度、溫度信號，確定真實的指示空速，供飛行員進行故障狀態改出。各信號及其來源如表3所示。

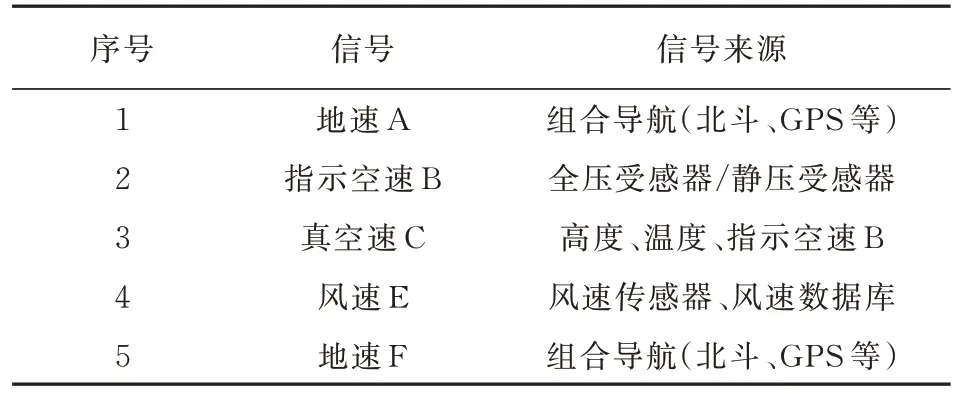
表3 信號及其來源T able 3 Signals and their sources

（1）風速計算原理

飛機風速的計算公式為

式中：

V

為北向風速；

V

為東向風速；

V

為天向風速；

V

為北向速度；

V

為東向速度；

V

為天向速度；

V

為真空速；

α

為真攻角；

J

為機體坐標系到地理坐標系的轉換矩陣。

J

的計算公式為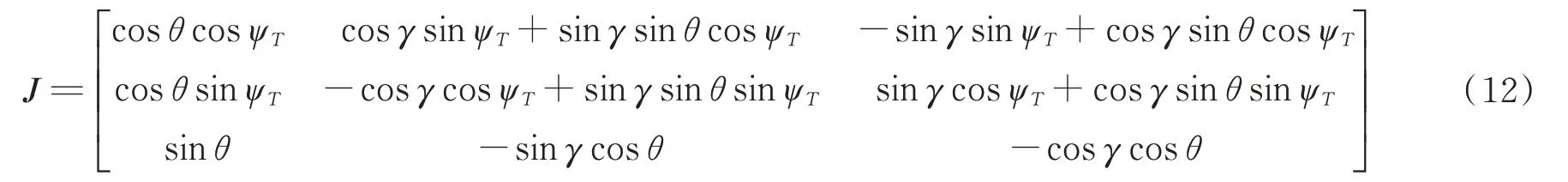

式中：

θ

為俯仰角；

ψ

為真航向角；

γ

為橫滾角。風速

V

計算公式為

航行風向

ψ

計算公式為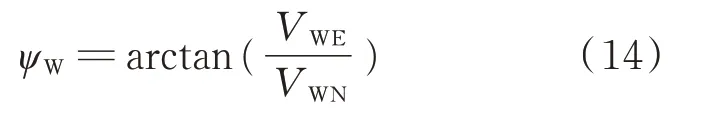

風向為風速矢量與正北的夾角，以正北為基準順時針為正。

在仿真時，大氣擾動使用大氣紊流的Dryden模型，速度自功率譜函數如下：

式中：

?

(

Ω

)為水平前向風；

?

(

Ω

)為側向風；

?

(

Ω

)為垂直風；

Ω

為空間頻率；

L

，

L

，

L

為紊流尺度；

δ

，

δ

，

δ

為風速的均方值。

（2）仿真驗證

在飛機總質量143 000 kg，重心0.260 7，高度1 000 m，馬赫數0.3，襟翼收起，起落架放下，真空速100.92 m/s，迎角5.225°，側滑角-4.114 1°，油門開度10.68°的平衡狀態下，開展試驗。

仿真總時長200拍，每拍0.02 s，在仿真0.2 s時，加入大氣紊流，紊流尺度533.4 m，翼展60 m，仿真結果如圖6所示。

圖6 加入大氣紊流的仿真結果Fig.6 Simulation results of atmospheric turbulence

從圖6可以看出：對于小幅度的大氣紊流，自動飛控可完成飛行狀態調節，且在0.2 s空速異常時刻，通過風速可重構出正確的空速101.41 m/s。

2.4 飛行狀態符合性判斷

在大飛機的飛行剖面中，巡航階段占據多數時間。基于大飛機的平衡狀態點，構造平衡狀態點知識庫。當在巡航階段平飛時，從知識庫中選取空速，與余度表決的空速值對比，如果差值大于臨界值，將進行不匹配告警，并建議切換到人工模式進行安全控制。臨界值的設定來源于外場飛機飛參數據。目前，臨界值選取為余度表決值的10%，隨著試飛驗證，臨界值將不斷完善。算法原理如圖7所示。

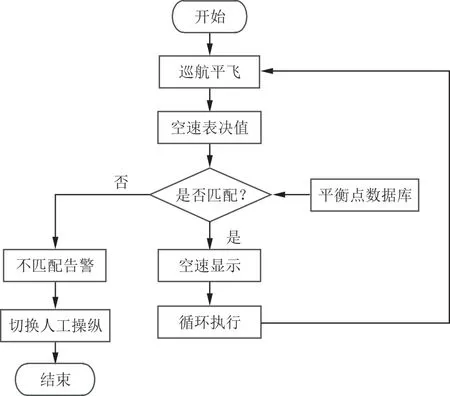
圖7 飛行狀態符合性判斷算法原理Fig.7 Principle of the algorithm for judging compliance of flight state

大飛機縱向力和力矩平衡方程為

式中：

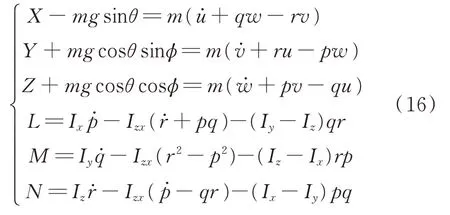
X

，

Y

，

Z

分別為體軸坐標系下

x

，

y

，

z

軸方向飛機所受的合力；

L

，

M

，

N

分別為體軸坐標系下

x

，

y

，

z

軸方向飛機所受的力矩。

（1）平衡狀態分析

在飛行包線范圍內，選取大飛機的平衡點。在總質量143 000 kg，重心0.260 7，襟翼收起，起落架放下的條件下，給出50組不同高度、速度、迎角下的狀態初值，進行批處理，得到相應的狀態平衡點。

對狀態平衡點的高度、真空速、迎角、升降舵偏角、油門桿參數進行歸一化處理后，進行多元線性回歸分析，得到回歸模型以構建平衡狀態點知識庫。以二元線性模型為例，回歸模型為

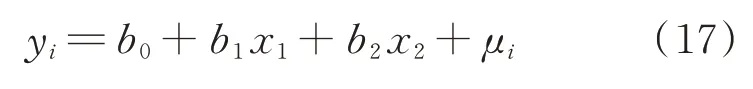
類似的使用最小二乘法進行參數估計：

計算結果如下：相關系數為0.983 7，

F

統計量值為679.294，

F

校驗的

p

值為0，誤差方差為0.000 7。由計算結果可知，相關系數接近1，回歸性好，檢驗的

p

值<0.01，擬合模型有效。繪制試驗狀態點的高度、迎角、真空速值，如圖8所示，可以看出：與計算結果相吻合。

圖8 多元線性回歸分析Fig.8 Multivariate linear regression analysis

在飛行包線內，自變量為高度、真空速、迎角、升降舵側滑角、油門開度參數，構建真空速知識庫。試驗狀態點的預估真空速與模型仿真的真空速的差值如圖9所示。

圖9 預估真空速差值Fig.9 Estimated true speed difference

從圖9可以看出：預估真空速差值的最大值為13.53 m/s，最小為-14.82 m/s，以模型仿真的真空速為基準，計算真空速差值百分比，最大為7.06%，在誤差范圍8%以內，平衡狀態點知識庫可以作為重構空速的來源。

（2）仿真驗證

在 總 質 量143 000 kg，重 心0.260 7，高 度1 000 m，馬赫數0.3，襟翼收起，起落架放下，真空速100.92 m/s，迎角5.225°，側滑角-4.114 1°，油門開度10.68°的平衡狀態下，開展試驗。仿真總時長200拍，每拍0.02 s，在仿真0.2 s時，注入空速共模故障和高度共模故障，飛行高度增加50 m，真空速增加0.05

Ma

，仿真結果如圖10所示。

圖10 空速異常仿真結果Fig.10 Simulation results of airspeed anomalies

從圖10可以看出：飛機將進入新的平衡點，參數為：高度1 050 m，真空速117.7 m/s，迎角3.604°，側滑角-3.027°，油門開度11.49°；通過知識庫計算的真空速為119.28 m/s，與仿真的真空速誤差為1.34%，可作為巡航階段平飛狀態的空速重構值。

3 結 論

（1）針對傳感器故障時飛行員輔助方法研究較少的問題，本文設計了大飛機空速異常輔助決策功能空速構建方法。通過余度表決判斷算法、飛行狀態符合性判斷算法、基于風速的空速構建算法和基于升力方程的空速構建方法，可有效識別空速故障信號，并構建真實的空速值，輔助飛行員完成故障改出操縱。

（2）考慮到模型和算法的數學本質，本文提出的空速異常輔助決策功能空速構建方法同樣可用于其他大飛機。