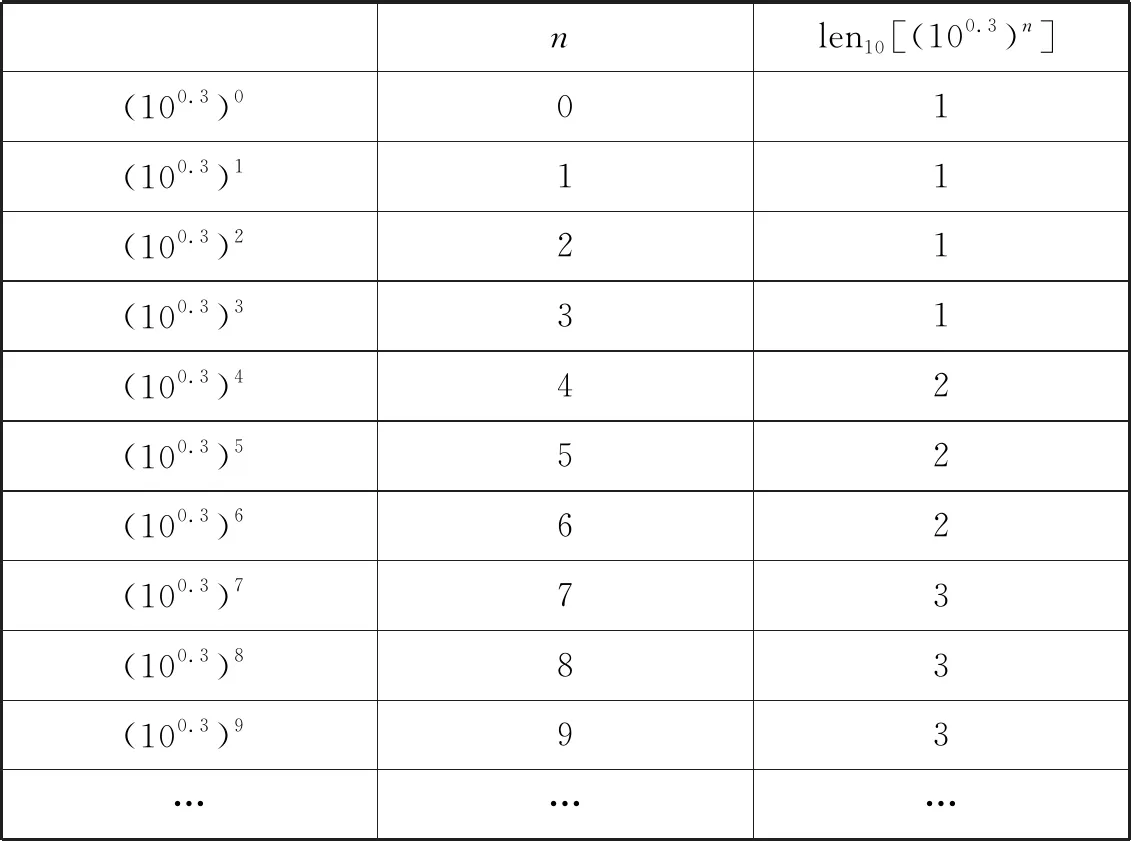
乘方的指數(shù)與其冪的位數(shù)的關(guān)系
劉耕滔, 謝子康
(1.浙江師范大學(xué) 數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,浙江 金華321004;2.浙江師范大學(xué) 物理與電子信息工程學(xué)院,浙江 金華321004)
1 引 言
眾所周知,bn(b>1,n∈)中隨著n的增大,其冪呈爆炸式增長.但經(jīng)過研究發(fā)現(xiàn),對應(yīng)于某些底數(shù)b,隨著n的增大其冪的數(shù)位呈某種周期循環(huán)規(guī)律(如附錄中的例子),目前尚無理論明確指出其間到底存在怎樣的規(guī)律.于是我們由此展開研究,探究了其背后的理論體系,并將其推廣到了更一般的情況.
2 預(yù)備知識
定義1位數(shù):一個(gè)自然數(shù)數(shù)位的個(gè)數(shù). 進(jìn)制:即進(jìn)位計(jì)數(shù)制,帶進(jìn)位的計(jì)數(shù)方法.
定義2定義一種函數(shù):取位函數(shù)(長度函數(shù))
f(x)=lenA(x) (A為大于1的常數(shù),x∈+).
該函數(shù)表示在A進(jìn)制下x的整數(shù)部分的位數(shù)為f(x).
根據(jù)定義,當(dāng)x∈[1,+∞)存在取位函數(shù)恒等式: lenA(x)= [logAx]+1.
定義3在A進(jìn)制下,若以b為底的冪bn的整數(shù)部分位數(shù)相同的乘方的個(gè)數(shù)是其指數(shù)的一個(gè)周期函數(shù)時(shí),則稱A進(jìn)制下bn的進(jìn)位定律存在.在該周期函數(shù)的最小正周期內(nèi)統(tǒng)計(jì)每一個(gè)位數(shù)所對應(yīng)的指數(shù)的個(gè)數(shù),將其數(shù)字按先后順序記下,便構(gòu)成了一個(gè)進(jìn)位循環(huán)組.進(jìn)位循環(huán)組中每一個(gè)數(shù)字(自然數(shù))為進(jìn)位循環(huán)段.表示進(jìn)位循環(huán)組時(shí),數(shù)字以西文逗號隔開,寫在括號內(nèi).(如附錄中的例子)(A,b∈且A,b>1,n∈).
進(jìn)位循環(huán)組表示進(jìn)位定律存在的乘方的冪的整數(shù)部分的周期性的進(jìn)位模式.
例1(100.3)n(n∈) 隨n增大時(shí)存在進(jìn)位定律,進(jìn)位循環(huán)組為 (4,3,3).
3 兩個(gè)定理
定理1(滿進(jìn)定理) 設(shè)A,a>1,n∈,當(dāng)且僅當(dāng)A=a時(shí),lenA(an)=n+1.
該定理結(jié)合數(shù)學(xué)歸納法易證.稱A進(jìn)制下an=An這種進(jìn)位的模式為“滿進(jìn)”.由定理指出,一種進(jìn)制下只存在一種滿進(jìn)情況.同樣結(jié)合數(shù)學(xué)歸納法,可以由定理1推得以下五個(gè)等價(jià)命題:A,a∈且A,a>1,n∈.在A進(jìn)制下,
(i)an為滿進(jìn);
(ii)A=a;
(iii)an的冪的位數(shù)等于其乘方的指數(shù)+1;
(iv)an的進(jìn)位循環(huán)組為(1);
(v)an的冪分別為“1,10,100,…(A進(jìn)制)”.
實(shí)際上遇到的更多情況并非是滿進(jìn)的,下面給出一條描述“非滿進(jìn)”(即b≠A)情況的定理.
定理2(非滿進(jìn)定理) 設(shè)A,b∈且A,b>1,n,l∈且l≥2,在A進(jìn)制下:
若b>A,則存在n,l,使得lenA(bn+1)=lenA(bn)+l;
若b 證當(dāng)b>A時(shí),設(shè)A=a,r,m∈+,則?r(r>1),使得b=r·a,進(jìn)而有b0=r0·a0,bn=rn·an.又因?yàn)閞>1,所以rn>1且rn單調(diào)遞增.顯然,?m∈,使得rm>10(A進(jìn)制),則有bm>10·am(A進(jìn)制)根據(jù)鴿巢原理與定理1,?n≥m,使得lenA(bn+1)=lenA(bn)+l(l∈且l≥2). 同理可證b 定義4在A進(jìn)制下,對于底數(shù)為b的乘方,將logAb稱為指律因子. 由定義可知,在A進(jìn)制下的指律因子與乘方的底數(shù)是一一對應(yīng)的. 定理3(進(jìn)位定律存在判別法) 在A進(jìn)制下,bn進(jìn)位定律存在的充要條件為指律因子logAb為有理數(shù)(A,b∈且A,b>1). 證必要性.若進(jìn)位定律存在,則由定義該周期循環(huán)關(guān)系必可被一個(gè)固定的進(jìn)位循環(huán)組描述,且該進(jìn)位循環(huán)組的兩個(gè)參數(shù):進(jìn)位循環(huán)組中數(shù)字的個(gè)數(shù)=g,進(jìn)位循環(huán)組中數(shù)字之和=k,為兩個(gè)有限大的正整數(shù).由進(jìn)位循環(huán)組的定義可知,g為經(jīng)歷一個(gè)進(jìn)位循環(huán)組時(shí)數(shù)位的增加量,k為經(jīng)歷一個(gè)進(jìn)位循環(huán)組時(shí)冪的指數(shù)的增加量,即Ag=bk(在A進(jìn)制下,An滿進(jìn)). 對于必要性的證明可逆,因此充分性可證.定理3證畢. 推論A進(jìn)制下,bn進(jìn)位定律存在的充要條件:互質(zhì)的兩參數(shù)g(進(jìn)位循環(huán)組中數(shù)字的個(gè)數(shù)),k(進(jìn)位循環(huán)組中數(shù)字之和)惟一存在且不為無窮. 根據(jù)上述理論,有以下求進(jìn)位循環(huán)組的方法. 在A進(jìn)制下,設(shè)指律因子α為有理數(shù). 求解p·α<1(p∈)中p的最大取值p1,則進(jìn)位循環(huán)組中第1個(gè)進(jìn)位循環(huán)段為p1+ 1; 再求解p·α<2(p∈)中p的最大取值p2,則進(jìn)位循環(huán)組中第2個(gè)進(jìn)位循環(huán)段為p2-p1; 再求解p·α<3(p∈)中p的最大取值p3,則進(jìn)位循環(huán)組中第3個(gè)進(jìn)位循環(huán)段為p3-p2; …… …… 依此類推,進(jìn)位循環(huán)組中除第1個(gè)進(jìn)位循環(huán)段為p1+ 1外,其余第m個(gè)進(jìn)位循環(huán)段為pm-pm-1. 該方法可整理為如下方程組 其中p∈,xi∈(i=1,2,3,…,g),xi為進(jìn)位循環(huán)組中第i個(gè)進(jìn)位循環(huán)段. 注 當(dāng)指律因子為無理數(shù)時(shí),進(jìn)位循環(huán)組不存在,但亦可將進(jìn)位循環(huán)組看作是周期為無窮大,再由上法求出足夠多的進(jìn)位循環(huán)段,以提高精確度,達(dá)到應(yīng)用目的. 設(shè)A,b,d∈且A,b,d>1,n∈,A進(jìn)制下bn進(jìn)位定律存在,則有以下四條性質(zhì): 性質(zhì)1(周期循環(huán)性)bn的整數(shù)部分位數(shù)相同的乘方的個(gè)數(shù)是其指數(shù)的一個(gè)周期函數(shù). 性質(zhì)2(組合性質(zhì)) 在A進(jìn)制下,若bn,dn都存在進(jìn)位定律,則(b·d)n也存在進(jìn)位定律,且其指律因子為logAb+logAd. 推論(i)在A進(jìn)制下,若bn存在進(jìn)位定律,dn不存在進(jìn)位定律,則(b·d)n不存在進(jìn)位定律; (ii)在A進(jìn)制下,若bn,(b·d)n存在進(jìn)位定律,則dn一定存在進(jìn)位定律; (iii)在A進(jìn)制下,若(b·d)n不存在進(jìn)位定律,則bn,dn至少有一個(gè)不存在進(jìn)位定律. 性質(zhì)3(進(jìn)位循環(huán)段的有界性) 進(jìn)位循環(huán)組中,第j個(gè)進(jìn)位循環(huán)段xj(j∈{2,3,…,g})僅有2個(gè)可能的數(shù)值:xj=x1或xj=x1-1. 證此性質(zhì)的證明過程借助以下引理. 引理1對于第3部分中求進(jìn)位循環(huán)組的方法中的條件,有以下等價(jià)形式 引理1可將第3部分中求進(jìn)位循環(huán)組的方程組改寫為如下形式(其它條件相同) 取j∈{2,3,…,g},則由方程組有 (1) 以及 (2) 聯(lián)立(1),(2)兩個(gè)不等式可以得出結(jié)論-1 性質(zhì)3證畢. 性質(zhì)4(進(jìn)位循環(huán)組的弱對稱性) 設(shè)進(jìn)位循環(huán)組為(x1,x2,…,xg),則有x1=xg+1且x2=xg-1,x3=xg-2,…成立. 證bk=Ak·α=Ag為g+1位數(shù),b0=A0=1為1位數(shù),因此第3部分中求進(jìn)位循環(huán)組的方程組中p∈[0,k)∩.去除左端點(diǎn),則p∈(0,k)∩,(0,k)為關(guān)于對稱的區(qū)間,對應(yīng)方程組的解中x1應(yīng)改為x′1=p1=x1-1 又由該方程組等價(jià)形式可得另一等價(jià)形式 兩等價(jià)形式的解相同.而后一等價(jià)形式的解的意義依次為:在區(qū)間(0,k)上的進(jìn)位循環(huán)組中由末至初的進(jìn)位循環(huán)段,與前一等價(jià)形式的解的意義恰好相逆(前一等價(jià)形式的解依次代表對稱區(qū)間(0,k)上進(jìn)位循環(huán)組中由初至末的進(jìn)位循環(huán)段),因此有x1=xg+1且x2=xg-1,x3=xg-2,…成立. 性質(zhì)4證畢. 本文研究了在一定進(jìn)制下,乘方的指數(shù)與其冪的位數(shù)的相關(guān)規(guī)律.其中定理1和定理2描述了乘方的指數(shù)與其冪的位數(shù)之間規(guī)律的框架,在定義了指律因子后便對規(guī)律的存在性以及規(guī)律的求解方法進(jìn)行了討論,最后給出四條規(guī)律存在時(shí)的相關(guān)性質(zhì),在某些情況下,判定進(jìn)位定律存在后,可以直接根據(jù)性質(zhì)求出進(jìn)位循環(huán)組.本文研究方法基于初等數(shù)論,采用數(shù)論中的方法,可對本文內(nèi)容繼續(xù)拓展延伸. 致謝感謝相關(guān)文獻(xiàn)對本文的啟發(fā)以及審稿專家提出的寶貴建議,感謝浙江師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院朱偉義教授的細(xì)心指導(dǎo)! 附 錄 以(100.3)為底的乘方當(dāng)指數(shù)n=0,1,2,…時(shí),其對應(yīng)冪如下表 表1 (100.3)n的指數(shù)與其冪的數(shù)字位數(shù)的關(guān)系表 除上表所列可以繼續(xù)向下驗(yàn)算,不難發(fā)現(xiàn),從n=0至n=9十個(gè)數(shù)可以作為一個(gè)最小正周期,其中整數(shù)部分為一位數(shù)的有4個(gè)、兩位數(shù)的有3個(gè)、三位數(shù)的有3個(gè),則其進(jìn)位循環(huán)組為(4,3,3),此進(jìn)位循環(huán)組中有三個(gè)進(jìn)位循環(huán)段,分別為“4”“3”“3”.另外,當(dāng)以2為底時(shí),雖然大多數(shù)也為“4,3,3”的規(guī)律,但在n=103,n=196,n=299等(len10(2103)=32,len10(2196)=60,len10(2299)=91)情況下失去了規(guī)律. 由前文定義可知進(jìn)位循環(huán)組、進(jìn)位循環(huán)段的意義:進(jìn)位循環(huán)組代表了一個(gè)冪的整數(shù)部分位數(shù)與其乘方的指數(shù)之間的規(guī)律性關(guān)系,進(jìn)位循環(huán)組中每一個(gè)數(shù)字為進(jìn)位循環(huán)段,表示整數(shù)部分同處于某一對應(yīng)位數(shù)下的冪的個(gè)數(shù),進(jìn)位循環(huán)段的個(gè)數(shù)表示經(jīng)過一個(gè)進(jìn)位循環(huán)冪的整數(shù)部分所進(jìn)的位數(shù),進(jìn)位循環(huán)組中數(shù)字之和表示一個(gè)進(jìn)位循環(huán)所占的乘方的指數(shù)的個(gè)數(shù).4 指律因子
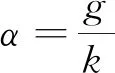
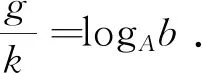
5 相關(guān)性質(zhì)
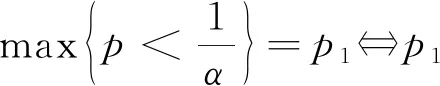

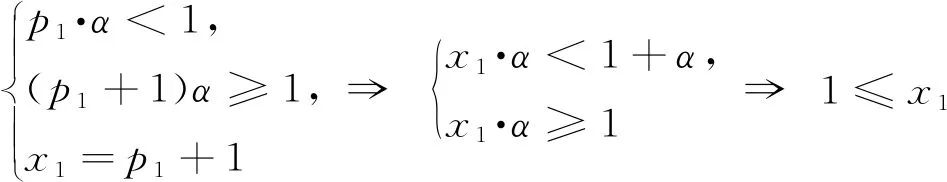
6 結(jié) 論