基于層次分析法的大學生高等數學成績影響因素分析

連高社， 陳小彪

(太原工業學院 理學系，太原030008)

1 引 言

高等數學是理工科專業普遍都會開設的一門重要的基礎課程.高等數學不僅僅對于學生學習專業課程有一定的重要基礎作用，而且對于學生學習能力的培養、理性思維的創建、應用意識的提高、創新意識的培養等同樣有著不可估量的作用.

然而，近幾年來很多高校大學生在學習高等數學的過程中出現了很多的問題.比如，部分學生學習高等數學的效果差、考試掛科現象屢見不鮮，更有甚者，有些高校的某些班級考試通過率竟然不到50%.從出現的各種問題來看，無論是各個高校，或者高等數學老師，還是學習高等數學的大學生，盡可能充分了解高等數學學習成績的影響因素已經成為當下的首要任務[1]，只有這樣，才能找準病因，對癥下藥，幫助大學生提高高等數學的學習成績.同時，對傳統課堂下影響成績的因素進行分析，也可以為后續高等數學課程教學改革的明確主要方向[2-3].通過數學模型對高等數學成績影響因素進行量化分析，可以幫助老師和學生找到提高成績的主要因素，提高教學質量，一些專家學者進行了相關研究.錢超[4]采用分層線性模型分析了高考數學成績和高等數學成績的關系.孫茜，蔡擇林[5]選取學生性別、學生對高等數學學習的興趣、數學學習對專業的有用性、高考成績等 12 個因素，建立了多元線性回歸分析模型進行線性回歸分析.吳國榮等[6]通過多重響應分析高等數學成績影響因素，主要包括學習興趣、課上聽課狀態、課下學習狀態、學習計劃、學習習慣.線性回歸模型可以分析變量之間的相關關系和影響系數，但對于變量之間的因果關系缺乏深層次的理解.層次分析法[7]可以根據研究目標的性質和要達到的總目標，將問題分解為不同的組成因素，并按照因素間的相互關聯影響以及隸屬關系將因素按不同層次聚集組合，形成一個多層次的分析結構模型，相較回歸模型能更好結合老師的教學經驗和學生的切身感受進行有效的問卷調查和權重的設計，真實的反映學生自身的學習狀況和困擾，判斷影響因素對于目標層的影響方式.

2 高等數學學習成績影響因素

以太原工業學院在校2018級大一學生為研究對象，對大學生學習高等數學的情況進行問卷調查.設計問卷時按照主題明確、結構合理、通俗易懂、適當控制問卷長度、方便資料的校驗、整理和統計[8]等原則進行.

針對于高等數學學習成績的影響因素進行問卷調查，總共分為五個層次，分別是個人、班級、學校、家庭和社會，每個層次里邊設置相應的各個具體影響因素，數量不等，本次問卷調查設置的問題內容，如下表1.

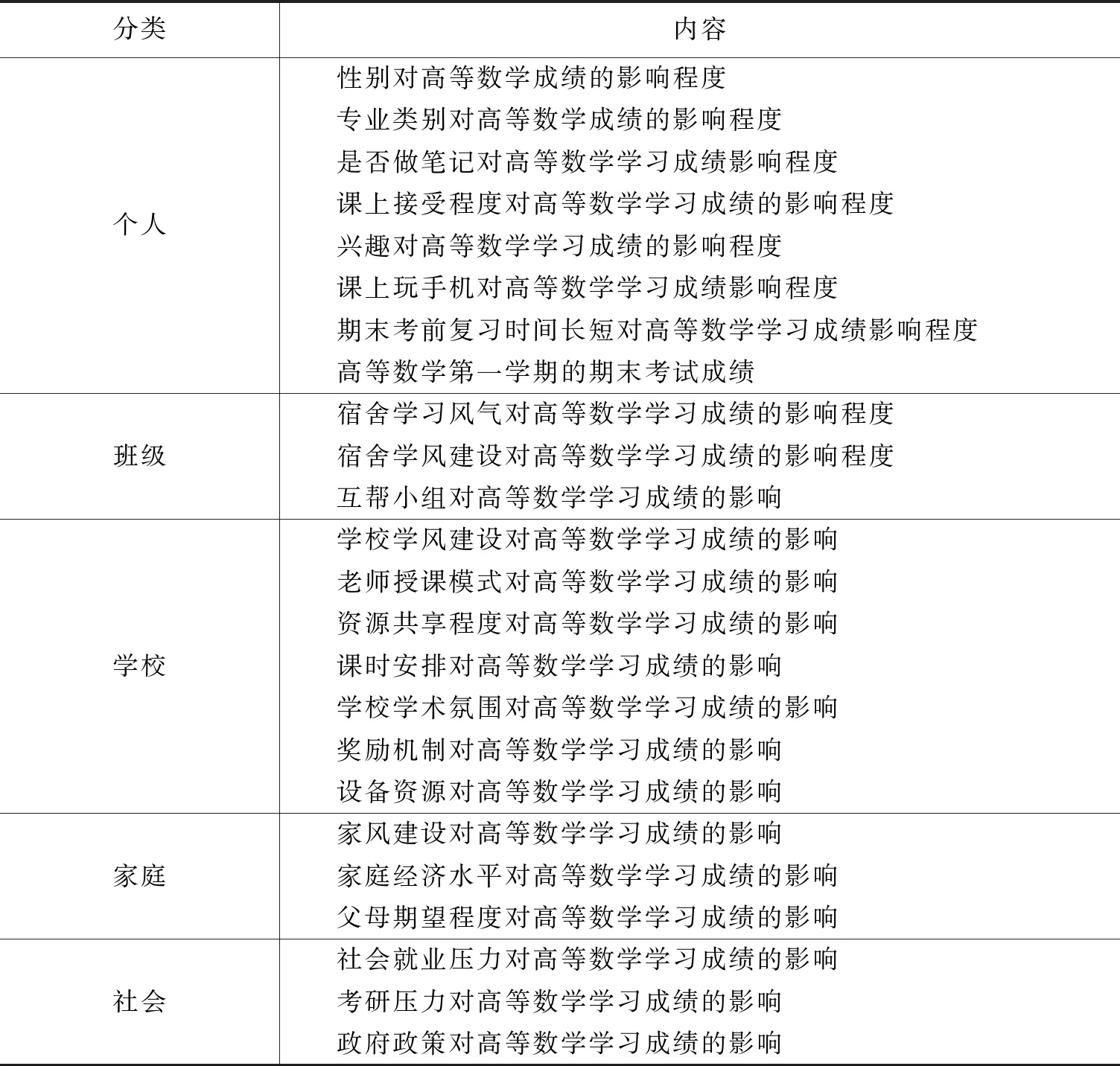
表1 問卷調查問題表

問卷主要從五個方面進行調查，每個方面包含大學生高等數學學習影響的具體因素，一共有24個問題因素.

本次調查共回收問卷225份，經過后期對數據的統計與整理，篩選出25份無效試卷，最終有200份數據可以作為本次調查的數據來源，對問卷數據進行了信度和效度檢驗，表現良好.

3 高等數學成績層次分析模型的建立和求解

3.1 高等數學成績影響因素層次結構的建立

將大學生高等數學學習成績的影響因素按照層次結構劃分為3個層次：目標層A、準則層Bi和子準則層Cj.目標層為大學生高等數學成績的影響因素，準則層分為五個因素，即為個人、班級、學校、家庭以及社會對大學生學習高等數學的影響因素，對五個準則層分解出更多的子準則層，例如個人層次考慮性別、專業類別、課程接受度、課堂上是否做筆記、對高等數學這門的興趣度等；班級層次考慮宿舍的學習風氣、學風建設以及互幫小組的成立是否有效，學校層次考慮高等數學課程的授課模式、學校的學術氛圍、課程學習資料的共享程度、獎勵機制等；家庭層次中家風建設、家庭經濟水平以及父母的期望；社會層次中社會就業壓力、考研壓力以及政府的教育政策.如下表2.

表2 影響大學生高等數學成績因素層次表

準則層中的因素對上一層的因素有影響，子準則層中的所有因素對于目標層都有影響，但是對于上一層來說，只對從屬于上一層的因素有影響，但是子準則層中的各個因素相互獨立，互不影響.

3.2 判斷矩陣一致性檢驗及層次單排序

通過對大學生高等數學影響因素的分析，對五個準則層即個人、班級、學校、家庭和社會，以及相對應的子準則層的因素分析，分別建立準則層對目標層、方案層對準則層的判斷矩陣，利用數學軟件 Matlab計算出判斷矩陣的最大特征值及特征向量，將特征向量進行歸一化，最后再做一致性檢驗:

(i) 判斷矩陣A-Bi

該矩陣的最大特征值λmax=5.1984，其對應的特征向量為

W1=(0.8388，0.4649，0.2332，0.0856，0.1362)T.

將W1歸一化可得到對應的權重為

WA=(0.4769，0.2643，0.1326，0.0487，0.0774)T.

一致性檢驗，一致性檢驗的指標：

平均一致性指標為

一致性比率CR1<0.1，矩陣A-Bi通過一致性檢驗.說明矩陣A-Bi構造合理，無需二次構造.

根據以上歸一化的權重WA可知：特征值0.0487最小，即家庭因素對于大學生學習高等數學的影響程度最小；特征值0.4769最大，即個人因素對于大學生學習高等數學的影響程度最大.

(ii) 判斷矩陣B1-Cj

由以上矩陣能夠得出

λmax=7.6323，W2=(0.0692，0.1356，0.2595，0.3829，0.5017，0.5683，0.4353)T.

歸一化后可得到的向量為

WB1=(0.0294，0.0576，0.1103，0.1627，0.2132，0.2416，0.1851)T.

進而得到一致性檢驗指標

一致性比率CR2<0.1，矩陣B1-Cj通過一致性檢驗，說明矩陣B1-Cj構造合理，無需二次構造.

根據以上歸一化的權重WB1可知：特征值0.0294最小，即性別因素對于大學生學習高等數學的影響程度最小；特征值0.2416最大，即考前復習因素對于大學生學習高等數學的影響程度最大，其次是權重占0.2132的課程興趣，學習興趣同樣對大學生學習高等數學有著重要的作用.

(iii) 判斷矩陣B2-Cj

由以上矩陣能夠得出

λmax=3.0735，W3=(0.3943，0.1722，0.9027)T.

歸一化后可得到的向量為

WB2=(0.2683，0.1172，0.6144)T.

進而得到一致性檢驗指標：

一致性比率CR3<0.1，矩陣B2-Cj通過一致性檢驗.說明矩陣B2-Cj構造合理，無需二次構造.

根據以上歸一化的權重WB2可知：特征值0.1172<0.2683<0.6144，由此可知班級內部的互幫小組對于大學生學習高等數學的影響程度所占比重最大，宿舍的學習風氣次之，班級學風建設對于班級層次的影響程度最小.

互幫小組不僅將學生個體間的學習競爭關系改變為“組內合作”“組間競爭”的關系，還將傳統教學中的師生之間的單向或雙向交流改變為師生、生生之間的多向交流，學生有更多的機會發表自己的看法，為他們提供一個較為輕松、自主的學習環境，提高了學生創造思維的能力，而且還將學生課內學習延伸到課外，使他們在參與學習的活動中得到愉快的情感體驗，從而更有利于高等數學的學習，對于提高高等數學的學習成績有很大的影響.

(iv) 判斷矩陣B3-Cj

由以上矩陣能夠得出

λmax=7.1067，W4=(-0.8703，-0.3073，-0.2807，-0.1383，-0.1357，-0.1357，-0.1159)T.

歸一化后可得到的向量

WB3=(0.4387，0.1549，0.1415，0.0697，0.0684，0.0684，0.0584)T.

進而得到一致性檢驗指標：

一致性比率CR4<0.1，矩陣B3-Cj通過一致性檢驗.說明矩陣B3-Cj構造合理，無需二次構造.

根據以上歸一化的權重WB3可知：特征值

0.0584<0.0684=0.0684<0.0697<0.1415<0.1549<0.4387，

由此可知學校層次中學風建設所占權重最大，老師的授課模式次之，其次是考試時的資源共享程度，而學校的設備資源對于大學生學習高等數學的影響程度最低.

(v) 判斷矩陣B4-Cj

由以上矩陣能夠得出為

λmax=3.0889，W5=(0.8500，0.4287，0.3061)T.

歸一化后可得到的向量為

WB4=(0.5363，0.2705，0.1931)T.

進而得到一致性檢驗指標：

平均一致性指標為

一致性比率CR5<0.1，矩陣B4-Cj通過一致性檢驗.說明矩陣B4-Cj構造合理，無需二次構造.

根據以上歸一化的權重WB4可知：特征值0.1931<0.2705<0.5363，由此可知：在家庭層次中，家風建設對于大學生高等數學學習成績的影響程度最高，其次是家庭的經濟水平，而父母的期望反而對于大學生高等數學的學習影響程度較低，所以一個家庭的家風建設也是尤為重要的，對于學生學習的狀態也有一定的影響.

(vi) 判斷矩陣B5-Cj

由以上矩陣能夠得出為

λmax=3.0889，W6=(0.8500，0.4287，0.3061)T.

歸一化后可得到的向量為

WB5=(0.5363，0.2705，0.1931)T.

進而得到一致性檢驗指標：

平均一致性指標為

一致性比率CR6<0.1，矩陣B5-Cj通過一致性檢驗.說明矩陣B5-Cj構造合理，無需二次構造.

根據以上歸一化的權重WB5可知：特征值0.1931<0.2705<0.5363，由此可知：在社會層次中，社會就業壓力對于大學生高等數學學習成績的影響程度最高，其次是考研壓力，而政府政策對于大學生高等數學的學習影響程度反而較低，而且根據權重占比，社會就業壓力所占比重基本一半還多，可見社會就業壓力對于大學生學習高等數學的影響程度有著不可估量的作用.

綜合對以上六個矩陣的計算，可得到如下高等數學大學生影響因素的層次單排序及一致性檢驗：

從表3可以看出，6個層次單排序的CR值均小于0.1，該六個層次單排序都通過一致性檢驗.其中矩陣B3-Cj的一致性檢驗比率最低，最高的比率是0.0775；特征值最大的為矩陣B1-Cj，同樣，一致性指標最大的也為矩陣B1-Cj.

表3 層次單排序計算及一致性檢驗

由上面的的單層次排序可知，單層次的權重排序比較單一，不能整體全面對大學生高等數學學習成績影響因素進行分析，還需要經過層次總排序才能直觀了解到所有的因素對于大學生學習高等數學的影響程度.

3.3 層次總排序及其一致性檢驗

構造成對比較矩陣，利用Matlab求得矩陣的最大特征值和對應的特征向量，將特征向量進行歸一化處理，進而得到權重W，WA是準則層對于目標層即高等數學學習成績影響因素的權重，WB是子準則層對于其相對應的準則層的權重，WC是所有的子準則層對于目標層的權重，計算各層次所有因素對高等數學學習成績的合成權重，將各層次進行總排序，各個矩陣的CR值都小于0.1，一致性檢驗通過.進行層次總排序后的合成權重結果見表4.

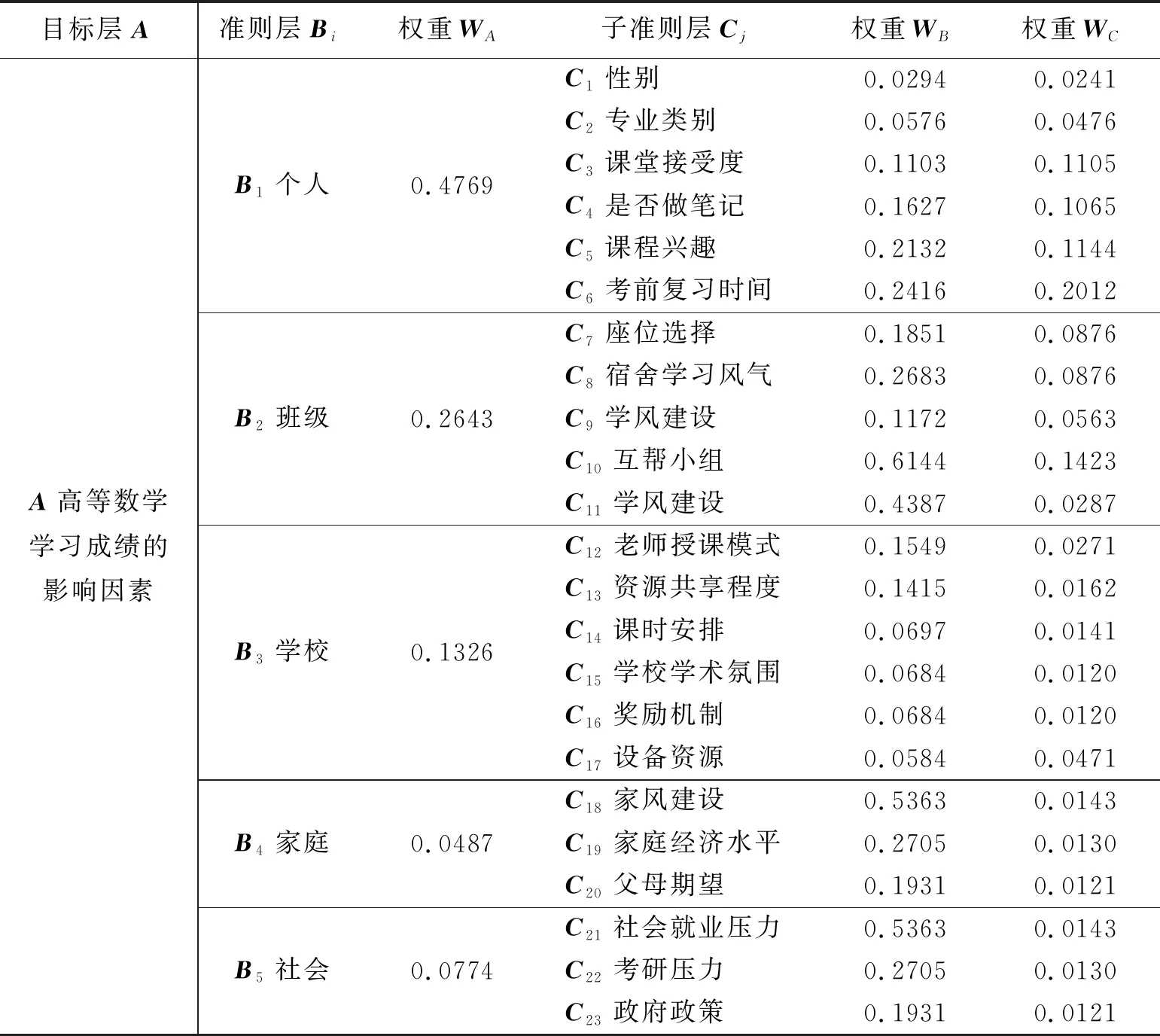
表4 高等數學學習成績影響因素的合成權重表

經層次總排序后發現：在個人層次中考前復習時間的權重值最高；班級層次中互幫小組的權重值最高；家庭層次中家風建設的權重值最高；社會層次中社會就業壓力的權重值最高.

4 結果分析與建議

根據上述層次結構分析結果，對于影響大學生高等數學學習成績的影響因素，提出如下結論和改進學習成績的具體措施：

(i) 在個人層次中，對于高等數學學習成績的影響因素，最重要的是每次考試前的復習時間(權重：0.2012)，考前復習對于一個考生來說，可謂是有著巨大的促進作用.平時的學習都是像蓋房子一樣，一磚一瓦慢慢堆積而成的，是一個基礎，如果地基打不好，那么最后的房子裝修的再華麗，都沒有用，也就是說，平時學習再多，如果考前不復習，不對所有的知識進行梳理的話，那么最后的結果還是不盡如人意.由此考前復習對于大學生學習高等數學也有著及其重要的作用.其次是學生對于高等數學的學習興趣，興趣是點燃智慧的火花，是探索知識的動力，如果學生慢慢培養起學習高等數學的興趣，那么學習高等數學將不再僅僅只是一件學習知識的枯燥無趣的事，更是一件充實自己的事情，在學習中找到樂趣，培養學習的主動性，從而提高大學生學習高等數學的成績[3]，學生的課程興趣(權重：0.1144)、課堂接受度(權重：0.1105)、課堂筆記(權重：0.1065)和上課座位選擇(權重：0.0876)也對高等數學學習成績有一定影響.

(ii) 在班級層次中，互幫小組(權重：0.1423s)對于大學生學習高等數學有著重要的作用，平時上課都是一位老師講課，下面一個班級的學生聽課，這樣的一對多教學，要想做到針對性很難.如果給一個班級成立幾個互幫小組，每個小組選取一位負責人，只負責該組成員的高等數學，給高等數學老師減壓，同時提高效率，方便學生一對一輔導學習，查漏補缺，自覺主動的去學習.所以大學生學習高等數學的過程中，在班級中成立互幫小組也是尤為重要，對提高學生的學習成績有很大的促進作用.班級的學風建設(權重：0.0563)也影響著高等數學的學習成績，如果一個班級有著良好的學習氛圍那么學生也會主動自覺的去學習，如果一個學校每個班級的課堂出勤率都是100%的話，學生的學習通常會很好，但是如果一個班級的到課率都不到50%，那么老師看著稀稀拉拉的座位，會降低老師授課的熱情，同樣，學生也沒有一個很好的學習氛圍體驗，在這樣的狀態下，學生的學習效率一定不會很高，進而高等數學的學習成績也不會很高，這樣會陷入惡性循環，結果是越來越差.

(iii) 在學校層次中，學習資源的豐富程度和學習資源的共享程度對高等數學成績有一定影響.

(iv) 在家庭層次中，家庭的家風建設對于大學生學習高等數學起到一定的促進作用.家庭是每個人的第一個課堂也是終身學堂，父母是孩子的第一任老師.家庭是教育的起點，家庭教育涉及很多方面，但最重要的是品德教育，是如何做人的教育[9].在學好做人的前提下，養成良好的學習習慣，積極主動地學習，那么把這種好習慣運用到學習高等數學上，最后的結果一定不會差強人意.

(v) 在社會層次中，大學生的社會就業壓力對于大學生學習高等數學同樣起著舉足輕重的作用.隨著每年大學畢業生的增加，大學畢業生的就業壓力越來越大，部分應屆畢業生選擇繼續深造，讀研，還有部分畢業生直接選擇進入社會，步入工作崗位，但是面對崗位少，擇業人多的情況，大學生的壓力也越來越大，同等條件下，畢業生上交單位的成績單也占很大的比重，所以需要大學生在上學期間，認真學習，努力提高高等數學的學習成績.由此，雖然就業是大學畢業之后的事情，但是在上大學期間，甚至從大一開始，就需要大學上努力學習高等數學，為之后的就業提前做好準備.

(vi) 在目標層中，占比最高的是準則層中的個人層(權重：0.4769)，其次是班級層(權重：0.2643)，排名第三的學校層(權重：0.1326)，家庭和社會層影響較小(權重均小于0.1).

5 結 論

提高高等數學課程的教學質量，需要重視影響教學質量和學習成績的因素，本文的研究表明，個人、班級、學校、家庭和社會，對于大學生高等數學的學習成績都有影響，其中起主要作用的是學生個人和班級層面.個人因素中關注學生對課程的興趣、課堂接受度、課堂筆記和上課座位選擇，班級因素中關注互幫小組和班級學風.高等數學任課教師可以在課程教學組織和課堂教學管理方面參與、組織和改進這些要素，提高教學質量.研究結論為今后進行高等數學的教學改革提供了思路和方向.

致謝本文的出發點在于研究影響大學生高等數學成績的因素，為改進高等數學教學質量提供幫助，感謝太原工業學院2015級數學與應用數學專業本科生武文娜和趙志新同學在調查問卷發放、數據搜集和初步整理等方面的給予文章的幫助，感謝本文審稿專家提出的寶貴意見.