SPH方法與經(jīng)典邊坡穩(wěn)定分析方法的對(duì)比研究

翟 明,李 亮，*,王上上,劉 旭,陳 富，楊正權(quán)

(1.青島理工大學(xué) 土木工程學(xué)院，青島 266033；2.中國水利水電科學(xué)研究院，北京 100048)

在眾多巖土問題中，邊坡失穩(wěn)事故尤為突出。作為巖土工程三大經(jīng)典問題之一，邊坡穩(wěn)定問題引起了國內(nèi)外學(xué)者的廣泛關(guān)注。目前常用的邊坡穩(wěn)定分析方法主要有三種，即極限平衡法(Limit Equilibrium Method, LEM)、強(qiáng)度折減法(Strength Reduction Method, SRM)和極限分析上限法(Upper Bound Limit Analysis Method)。極限平衡法[1-2]是最早用于邊坡穩(wěn)定分析的方法，目前已趨于完善和成熟。極限平衡法主要包括兩個(gè)步驟：①計(jì)算給定滑動(dòng)面的安全系數(shù)；②基于智能優(yōu)化算法變換不同的滑動(dòng)面并計(jì)算其安全系數(shù)，確定最小安全系數(shù)及其對(duì)應(yīng)的臨界滑動(dòng)面。強(qiáng)度折減法思想最早由ZIENKIEWICZ等[3]提出，后來被許多學(xué)者廣泛應(yīng)用于邊坡穩(wěn)定分析。強(qiáng)度折減法的基本思想是將土體初始抗剪強(qiáng)度參數(shù)(黏聚力c、內(nèi)摩擦角φ)不斷進(jìn)行折減，直至邊坡達(dá)到臨界狀態(tài)，此時(shí)的折減系數(shù)即為安全系數(shù)。極限分析上限法[4]的基本思想為：對(duì)于給定的失效模式，從變形協(xié)調(diào)出發(fā)，根據(jù)外力功和內(nèi)能消散相平衡的原理確定相應(yīng)的安全系數(shù)，然后應(yīng)用最優(yōu)化方法，確定相應(yīng)于最小安全系數(shù)的臨界失效模式。上述三種方法在邊坡穩(wěn)定分析中均有應(yīng)用，對(duì)于復(fù)雜荷載工況、復(fù)雜邊坡剖面的邊坡而言，如何檢驗(yàn)三種方法的適用性并比較其計(jì)算性能對(duì)于邊坡穩(wěn)定分析具有較強(qiáng)的指導(dǎo)意義。

近年來，光滑粒子流體動(dòng)力學(xué)(Smoothed Particle Hydrodynamics，SPH)方法[5-9]逐漸被用于巖土工程領(lǐng)域，BUI等[5]較早地將Druck-Prager本構(gòu)模型引入SPH方法中，進(jìn)行了一系列巖土工程問題的模擬，為SPH方法在巖土工程問題中的應(yīng)用奠定基礎(chǔ)。黃雨等[6]采用Bingham流體模型描述土體的流動(dòng)大變形，并進(jìn)行了SPH數(shù)值模擬，結(jié)果與模型試驗(yàn)實(shí)測數(shù)據(jù)基本吻合，表明SPH方法對(duì)于土體大變形分析的有效性。唐宇峰等[7]研究了SPH在邊坡穩(wěn)定計(jì)算中的失穩(wěn)判據(jù)，LI等[8]用SPH方法并結(jié)合極限平衡方法的安全系數(shù)模擬了邊坡臨界狀態(tài)時(shí)的位移云圖，在此基礎(chǔ)上評(píng)估了極限平衡方法的臨界滑動(dòng)面。由此可見，SPH方法能夠模擬滑坡從發(fā)生、運(yùn)動(dòng)直至最終土體堆積的整個(gè)過程，其位移場云圖可以結(jié)合強(qiáng)度折減法塑性剪應(yīng)變?cè)隽吭茍D，從而全面直觀地比較傳統(tǒng)分析方法的臨界滑動(dòng)面。在簡要敘述邊坡穩(wěn)定分析方法的基礎(chǔ)上，采用三個(gè)邊坡算例，分別比較了三種邊坡穩(wěn)定分析方法的結(jié)果，得出了有意義的結(jié)論。

1 方法介紹

1.1 極限平衡法

極限平衡法(LEM)是最早應(yīng)用于邊坡穩(wěn)定性分析的方法。極限平衡法大多以垂直條分法為基礎(chǔ)，通過引入條間力函數(shù)假定使問題變得靜定可解，從而利用力和力矩平衡方程得出邊坡穩(wěn)定安全系數(shù)。目前已有多種基于極限平衡理論的邊坡穩(wěn)定分析方法，如瑞典法、Bishop法、Janbu法、Spencer法、Morgenstern-Price法等。由于傳統(tǒng)的極限平衡法計(jì)算簡便、概念清晰，現(xiàn)在仍然是工程師所采用的主要方法。本文極限平衡法采用的計(jì)算程序?yàn)镚EOStudio中的SLOPE/W，計(jì)算方法選取常用的Spencer法。

1.2 強(qiáng)度折減法

(1)

式中：c，φ為土體的初始黏聚力和內(nèi)摩擦角；c′，φ′為折減后土體的黏聚力和內(nèi)摩擦角；F為折減系數(shù)。

本文采用強(qiáng)度折減法結(jié)合有限差分的數(shù)值計(jì)算程序FLAC軟件求解邊坡穩(wěn)定安全系數(shù)，采用塑性剪應(yīng)變?cè)隽吭茍D來查看滑動(dòng)區(qū)域。

1.3 極限分析上限法

極限分析上限法有很多實(shí)現(xiàn)途徑，本文采用最新提出的不連續(xù)布局優(yōu)化[10-11]方法(Discontinuity Layout Optimization，DLO)。不連續(xù)布局優(yōu)化使用嚴(yán)格的線性優(yōu)化技術(shù)識(shí)別分布在土體中節(jié)點(diǎn)之間的不連續(xù)discontinuity的關(guān)鍵布局，它可以識(shí)別塊體的滑動(dòng)和平移，能夠利用數(shù)學(xué)優(yōu)化技術(shù)識(shí)別關(guān)鍵的破壞滑移線。

DLO方法以節(jié)點(diǎn)來離散求解域，節(jié)點(diǎn)之間相互連接，形成多個(gè)不連續(xù)discontinuities(以下簡稱disc)，然后將土體參數(shù)賦予每個(gè)不連續(xù)disc，在荷載作用下，位移增大，外力做功也相應(yīng)增大，當(dāng)外力做功與系統(tǒng)的能量耗散相等時(shí)，達(dá)到極限狀態(tài)。采用數(shù)學(xué)優(yōu)化技術(shù)規(guī)劃多條可能的路徑，對(duì)路徑中每一個(gè)不連續(xù)disc進(jìn)行搜索，計(jì)算路徑的能量耗散，能量耗散最小的路徑即為破壞路徑。DLO方法確定破壞模式的過程如圖1所示，首先描述所要求解的問題(圖1(a))，然后以一定密度的節(jié)點(diǎn)離散所求解問題的幾何體(圖1(b))，節(jié)點(diǎn)之間相互連接形成不連續(xù)disc(圖1(c))，最后應(yīng)用有效的數(shù)學(xué)優(yōu)化技術(shù)得到破壞時(shí)的滑動(dòng)面(圖1(d))。需要注意的是，DLO的計(jì)算過程中，所布設(shè)的節(jié)點(diǎn)、方式、密度、本構(gòu)模型參數(shù)取值以及邊界條件的設(shè)定對(duì)結(jié)果都會(huì)有影響，本文所采用的計(jì)算程序?yàn)長imitState：GEO，采用其默認(rèn)設(shè)置，網(wǎng)格密度取中等。

圖1 DLO方法確定破壞模式的過程

1.4 光滑粒子流體動(dòng)力學(xué)方法(SPH)

SPH[5-9]是一種無網(wǎng)格的數(shù)值方法，與有限元等需要?jiǎng)澐志W(wǎng)格的數(shù)值方法不同，SPH方法用有限個(gè)粒子來離散問題域，不需要網(wǎng)格劃分和小變形假設(shè)，這使得SPH可以不受網(wǎng)格畸變問題的影響，因此，SPH方法可以直接用于模擬巖土工程的大變形問題。SPH的概念圖如圖2所示，每個(gè)粒子被賦予狀態(tài)變量(含有速度、位移、應(yīng)力、應(yīng)變等)和材料屬性(含有重度、黏聚力、內(nèi)摩擦角、彈性模量、泊松比等)。

圖2 SPH的概念

圖2中黑色實(shí)心圓圈所示的粒子i的信息通過核函數(shù)W與影響區(qū)域內(nèi)臨近粒子k相互作用來獲得，與影響區(qū)域外的粒子無關(guān)，影響區(qū)域通過變量h來確定。SPH方法中粒子的運(yùn)動(dòng)信息由質(zhì)量守恒方程(式(2))和動(dòng)量守恒方程(式(3))確定。

(2)

(3)

式中：N為粒子總數(shù)；ρ為粒子中土體的密度；m為粒子質(zhì)量；v為粒子的速度；t為時(shí)間；Wik為粒子i與粒子k間的光滑核函數(shù)；σ為單個(gè)粒子的總應(yīng)力張量，其表達(dá)式由土體的本構(gòu)模型確定；x為粒子位置；α，β為不同的坐標(biāo)軸；fα為外力引起的加速度分量。

根據(jù)式(1)～(7)可得:第10個(gè)考核期Cpv為3.976萬元，Cav為4.704萬元，Ev為3.96萬元，Vs為-0.016萬元，Vc為-0.744萬元，Is為1.034，Ic為0.842。由計(jì)算結(jié)果可知:該項(xiàng)目在第10個(gè)考核期實(shí)際安全成本投入處于超支狀態(tài)，實(shí)際安全保障水卻沒有達(dá)到計(jì)劃水平，可以排除是由于安全成本節(jié)約導(dǎo)致了安全度的降低，很明顯是由于管理措施不到位而造成的，項(xiàng)目經(jīng)理部應(yīng)結(jié)合專家對(duì)當(dāng)月安全評(píng)價(jià)體系的評(píng)分情況和項(xiàng)目實(shí)際安全投入情況進(jìn)行深入分析，找出原因，加強(qiáng)安全管理力度的同時(shí)嚴(yán)格控制安全成本的支出，保證項(xiàng)目施工安全順利開展。

SPH方法模擬巖土工程問題時(shí)，算法參數(shù)取值對(duì)計(jì)算結(jié)果有重要影響。譬如，核函數(shù)W，影響半徑h以及邊界問題處理時(shí)所需的人工黏性比例因子等。本團(tuán)隊(duì)基于SPH方法的基本原理與公式自編了Fortran程序，并進(jìn)行了3年的調(diào)試，與前人的研究結(jié)果進(jìn)行了對(duì)比，并發(fā)表了相關(guān)文章，可參閱文獻(xiàn)[8]。

2 SPH驗(yàn)證

應(yīng)用本團(tuán)隊(duì)自編SPH程序來模擬砂柱垮塌試驗(yàn)，模擬結(jié)果與HUNGR[12]所做的模型試驗(yàn)結(jié)果進(jìn)行對(duì)比，來驗(yàn)證自編SPH程序的可靠性。砂柱高度為0.2 m，寬度為0.4 m，密度ρ=1630 kg/m3，黏聚力c=0 kPa，內(nèi)摩擦角φ=30.9°。在SPH參數(shù)設(shè)置中，兩個(gè)主要的參數(shù)為粒子的間距與影響半徑h，MAO等在文獻(xiàn)[9]中對(duì)SPH方法的參數(shù)做了細(xì)致的研究，本文參數(shù)取值參考文獻(xiàn)[9]研究結(jié)果進(jìn)行。將粒子半徑取為0.005 m，影響半徑取為0.006 m，共產(chǎn)生3200個(gè)粒子，分析模型如圖3所示。

圖3 砂柱試驗(yàn)SPH分析模型

SPH方法的計(jì)算過程包含兩個(gè)步驟，首先模擬荷載作用下土的固結(jié)過程，固結(jié)完成以后，再模擬土體在荷載作用下的失穩(wěn)滑動(dòng)過程。SPH方法模擬砂柱垮塌后的形態(tài)與文獻(xiàn)[12]的試驗(yàn)結(jié)果對(duì)比如圖4所示。

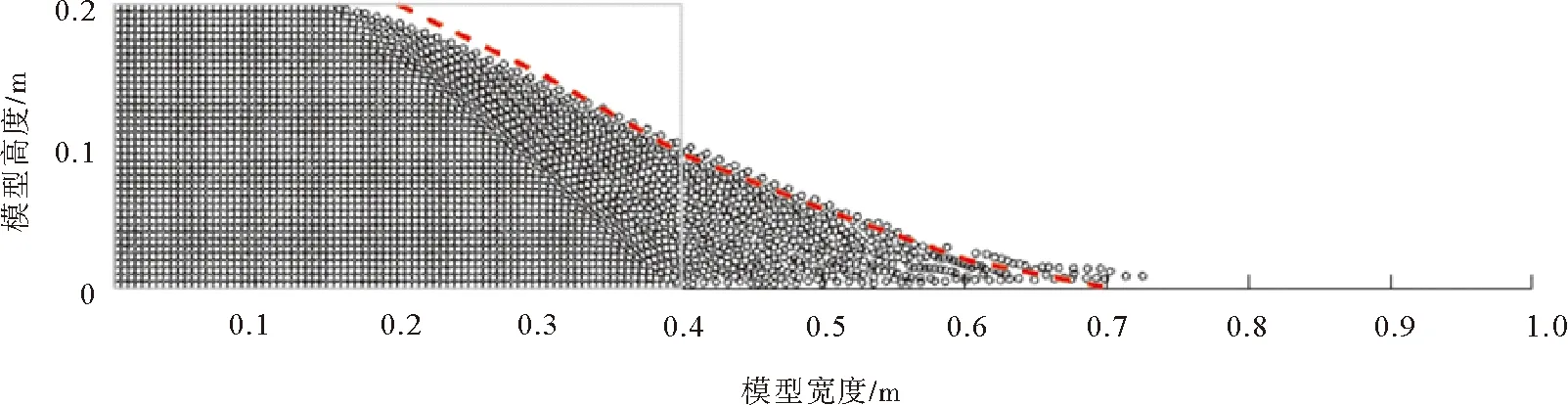
圖4 砂柱試驗(yàn)的SPH模擬與試驗(yàn)對(duì)比

圖4中，紅色線為砂柱垮塌試驗(yàn)完成后的坡面曲線。由圖4可知，SPH方法模擬的結(jié)果與實(shí)驗(yàn)室砂柱垮塌試驗(yàn)結(jié)果表現(xiàn)出了良好的一致性，所以，本團(tuán)隊(duì)自編SPH程序可以用于模擬滑坡過程中的大變形問題，其位移場云圖可以與強(qiáng)度折減法塑性剪應(yīng)變?cè)隽吭茍D一起來綜合衡量邊坡穩(wěn)定性問題。

3 算例分析

3.1 算例1

考慮圖5所示的簡單均質(zhì)邊坡，模型寬度為20 m，總高度為10 m，其中坡高為6 m，坡角45°。假設(shè)土體材料服從Mohr-Coulomb強(qiáng)度準(zhǔn)則，黏聚力c=20 kPa，內(nèi)摩擦角φ=17°，重度γ=19 kN/m3。

圖5 算例1模型

對(duì)于算例1，分別使用極限平衡法、強(qiáng)度折減法、不連續(xù)布局優(yōu)化法進(jìn)行分析，得到的安全系數(shù)分別為1.623，1.674和1.742。其臨界滑動(dòng)面和塑性貫通區(qū)如圖6所示。

圖6 算例1臨界滑動(dòng)面及塑性剪應(yīng)變?cè)隽吭茍D

通過圖6中三種方法結(jié)果的對(duì)比可知，極限平衡法和強(qiáng)度折減法所得安全系數(shù)基本一致，DLO所得安全系數(shù)略高；極限平衡法和不連續(xù)布局優(yōu)化法得到的臨界滑動(dòng)面非常接近，均落在強(qiáng)度折減法的塑性破壞區(qū)內(nèi)(由塑性剪應(yīng)變?cè)隽吭茍D確定)。所以，對(duì)于簡單的均質(zhì)邊坡，三種方法所得臨界滑動(dòng)面幾乎一致，安全系數(shù)略有差別。

應(yīng)用SPH方法分析該問題，將粒子半徑定義為0.1 m，影響半徑取為0.12 m共產(chǎn)生3965個(gè)粒子，SPH分析模型如圖7所示。利用原始參數(shù)進(jìn)行邊坡自重應(yīng)力的模擬，進(jìn)而將原始參數(shù)仿照強(qiáng)度折減法公式(1)進(jìn)行折減，折減系數(shù)取為LEM所得安全系數(shù)，即F=1.623，將折減后的參數(shù)輸入SPH程序，得到計(jì)算穩(wěn)定時(shí)刻的位移場云圖與LEM，DLO方法的臨界滑動(dòng)面比較如圖8所示。

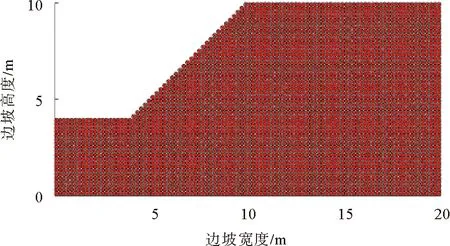
圖7 算例1的SPH分析模型

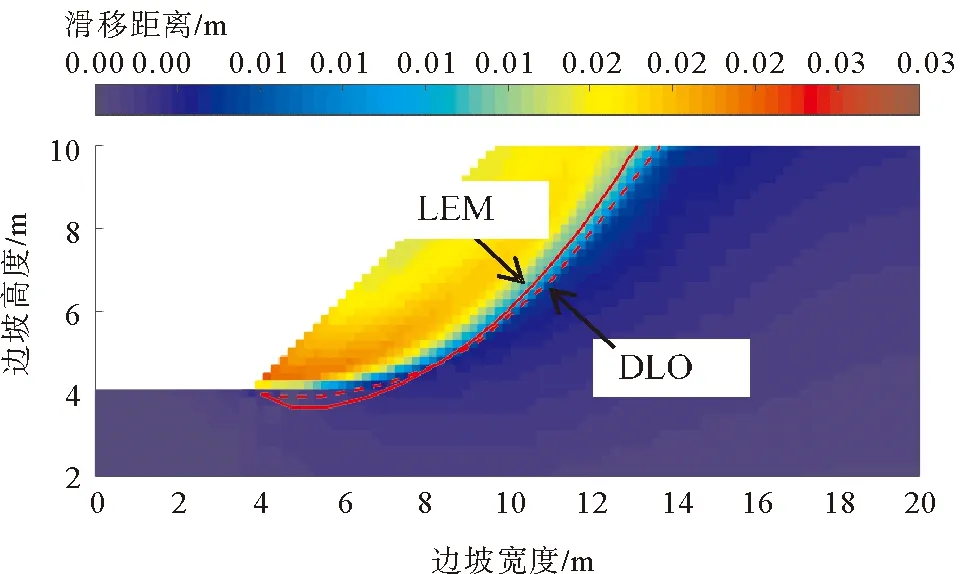
圖8 算例1的臨界滑動(dòng)面及SPH位移場云圖

由圖8可以看出，SPH得到的位移場云圖明顯分為藍(lán)色的不動(dòng)區(qū)與青色/黃色以及紅色所示的滑動(dòng)區(qū)，二者之間的分界線與LEM，DLO所得臨界滑動(dòng)面基本吻合，從而間接驗(yàn)證了強(qiáng)度折減法所得塑性剪應(yīng)變?cè)隽吭茍D與SPH位移場云圖在識(shí)別邊坡滑動(dòng)面方面的一致性。

3.2 算例2

邊坡的幾何尺寸與算例1保持一致，將土體黏聚力改為c=0 kPa，此時(shí)問題成為無黏性土坡的穩(wěn)定性問題，此時(shí)的安全系數(shù)應(yīng)為

(4)

式中：φ為土體的內(nèi)摩擦角；β為邊坡坡角。

極限平衡法得到的安全系數(shù)為F=0.33，破壞模式為表層破壞，與理論分析的結(jié)果一致。用強(qiáng)度折減法計(jì)算得到的安全系數(shù)為Fs=0.30，塑性剪應(yīng)變?cè)隽吭茍D如圖9所示，同樣為表層破壞模式。

圖9 算例2的SRM塑性區(qū)云圖

SPH方法得到的位移場云圖如圖10所示，同樣為沿表層的滑移破壞。

圖10 算例2的SPH方法滑動(dòng)位移

所以，極限平衡法、強(qiáng)度折減法以及SPH方法適用于無黏性土邊坡的穩(wěn)定性分析。而應(yīng)用DLO方法計(jì)算該問題時(shí)，折減強(qiáng)度后輸出的結(jié)果為“unknown”，折減荷載后的結(jié)果為“unstable”，均沒能給出一個(gè)確定的安全系數(shù)。將黏聚力調(diào)整為c=1 kPa時(shí)，結(jié)果仍然不能確定。這說明DLO方法不能很好地處理c接近于0的幾乎無黏性、純摩擦情況的邊坡穩(wěn)定問題。在實(shí)際工程中遇到此類情況時(shí)應(yīng)慎用DLO。

3.3 算例3

采用文獻(xiàn)[11]中的算例，算例幾何模型如圖11所示，材料參數(shù)見表1。高度為8 m的大壩(土層A)修建于成層土地基上，其中第一層土為強(qiáng)度較高的砂土層(土層B)，第二層為軟弱層(土層C)，最下層為基巖。

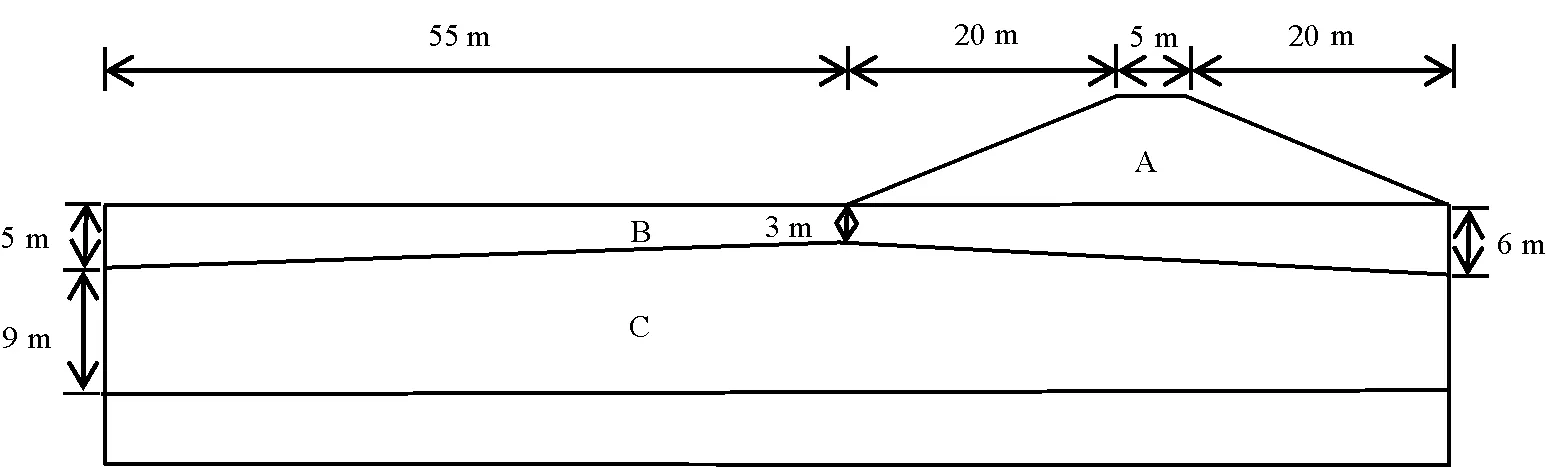
圖11 算例3的模型

表1 算例3土層參數(shù)

分別應(yīng)用LEM，SRM，DLO三種方法分析該問題，得到的臨界滑動(dòng)面、安全系數(shù)和塑性剪應(yīng)變?cè)隽吭茍D如圖12所示。需要指出的是：由于該邊坡為失穩(wěn)狀態(tài)，在SPH分析時(shí)，需要人為提高土層的強(qiáng)度參數(shù)以便獲取邊坡的自重應(yīng)力，然后再利用原始參數(shù)進(jìn)行滑坡過程的模擬。

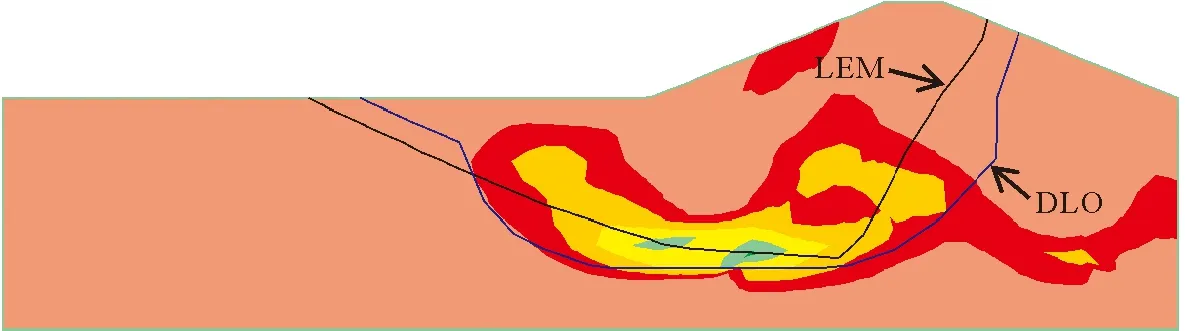
圖12 算例3的LEM，DLO臨界滑動(dòng)面及SRM塑性區(qū)云圖

由圖12可知，LEM，SRM和DLO得到的安全系數(shù)分別為0.875，0.86和1.106，LEM和SRM所得安全系數(shù)基本一致。DLO方法的安全系數(shù)與LEM比較，計(jì)算誤差為26.4%；與SRM比較，計(jì)算誤差為28.6%，誤差過大。

再分析該問題的臨界滑動(dòng)面，DLO方法得到的滑動(dòng)面在土層交界處均出現(xiàn)一個(gè)比較大的凸(凹)角，這與SPH位移場云圖吻合較好，而LEM的臨界滑動(dòng)面左右兩部分的趨勢(shì)變化不太明顯，這種較為常規(guī)的滑動(dòng)面在軟弱交替土層中出現(xiàn)似乎是不合理的。另外，滑動(dòng)面在軟弱帶中的部分，LEM的滑動(dòng)面沒有穿過軟弱帶到達(dá)基巖上部，而DLO方法的滑動(dòng)面以及SRM，SPH方法的塑性區(qū)均到達(dá)基巖表面(圖12、圖13)，這說明LEM尋找復(fù)雜邊坡問題臨界滑動(dòng)面的能力有待提高。這是因?yàn)長EM通常需要人為設(shè)置滑動(dòng)面形狀和滑入、滑出范圍，對(duì)于這種復(fù)雜的情況，潛在的滑入、滑出范圍不明顯，人為設(shè)置過于主觀，存在一定誤差。所以，對(duì)于確定復(fù)雜條件下邊坡失穩(wěn)的臨界滑動(dòng)面位置，DLO與SPH方法比LEM更加具有優(yōu)勢(shì)。

圖13 算例3的LEM，DLO臨界滑動(dòng)面及SPH塑性區(qū)云圖

對(duì)于幾何模型復(fù)雜、存在軟弱夾層等復(fù)雜地質(zhì)條件的邊坡穩(wěn)定性問題，建議應(yīng)用多種理論或軟件進(jìn)行分析，綜合考量以得出正確的結(jié)論來指導(dǎo)工程設(shè)計(jì)。

4 結(jié)論

1) 對(duì)于簡單的均質(zhì)邊坡，LEM，SRM和DLO方法均能得到令人滿意的結(jié)果，可以得出合理的安全系數(shù)以及臨界滑動(dòng)面，SPH模擬得到的位移場云圖與強(qiáng)度折減法所得塑性剪應(yīng)變?cè)隽吭茍D在識(shí)別臨界滑動(dòng)面方面具有一致性。

2) DLO方法對(duì)于接近無黏性、純摩擦土體的情況會(huì)出現(xiàn)不易收斂，甚至計(jì)算失敗的現(xiàn)象，遇到此類情況應(yīng)慎用DLO方法。

3) 對(duì)于幾何模型復(fù)雜、存在軟弱夾層等復(fù)雜地質(zhì)條件的邊坡穩(wěn)定性問題，在計(jì)算安全系數(shù)上，LEM與SRM所得安全系數(shù)基本一致，DLO方法所得安全系數(shù)偏高，誤差較大。在確定臨界滑動(dòng)面上，DLO方法的結(jié)果與SPH方法的位移場云圖十分一致，這是因?yàn)閮烧呔恍鑼?duì)滑動(dòng)面的位置做過多假設(shè)，對(duì)于確定復(fù)雜邊坡的臨界滑動(dòng)面表現(xiàn)出了明顯的優(yōu)勢(shì)。所以，對(duì)于復(fù)雜條件的邊坡穩(wěn)定問題，建議應(yīng)用多種理論進(jìn)行分析，綜合考量后得出合理結(jié)論。