連跨懸索橋中間鋼塔雙重非線性極限承載力研究

劉小林

(中鐵大橋勘測設計院集團有限公司 武漢 430056)

極限承載力和穩定性不但反映結構的運營安全性，也是工程設計和計算的重點及難點。橋梁結構極限承載力分析的實質是通過不斷求解計入幾何非線性和材料非線性的剛度方程，尋找其極限荷載的過程[1-2]。目前橋梁極限承載力常用的分析方法有：線性屈曲法、幾何非線性分析法及同時考慮幾何和材料非線性的雙非線性分析方法。通過對極限承載力的模擬，可以呈現極限狀態下的倒塌模式，發現結構的薄弱點、薄弱截面或薄弱構件，進而有針對性地補強和提高，以達到全橋各個構件和部位安全系數基本一致的目的。本文結合智利查考橋初步設計方案中的中間鋼塔，通過不同荷載工況下雙重非線性分析，從塑性鉸的形成機理出發，提出在有限元全橋倒塌仿真分析中通過屈曲點和屈服點先后關系識別破壞誘因及失效模式的方法，對懸索橋中間鋼塔的失穩機理和相對薄弱部位進行分析，并提出相應的補強措施，以增加運營階段的結構安全性。

1 方案概況

隨著連跨懸索橋的興起，由于其能適應特殊的地形環境，不但造型美觀，且造價方面具有較大的競爭優勢，在世界各地均有較多的推廣建造，由于連跨懸索橋中塔剛度大、受力復雜，其極限承載力得到了廣泛的關注。本文選取的研究對象為智利查考大橋初步設計方案，其總體布置為三塔懸索橋，跨度為140 m+1 055 m+1 100 m+339 m =2 634 m，中塔采用順橋向為人字形的鋼結構塔，邊塔為鋼筋混凝土塔，加勁梁采用扁平閉口鋼箱梁。懸索橋方案布置見圖1。

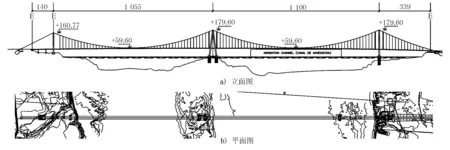
圖1 懸索橋方案總體布置圖(單位：m)

該方案為三塔雙主跨懸索橋，中間鋼塔承受主纜傳遞的很大的恒載軸力，在單主跨滿布活載等極限偏載情況下又可能出現較大彎矩。由于缺乏剛度較大的邊索約束，塔頂縱橋向剛度相對較弱，在大軸力或軸力、彎矩組合作用下可能發生多種局部屈曲、整體屈曲及材料屈服的破壞模式，造成數值分析困難，正確識別其發生破壞的誘因和失效模式是有針對性地提高其全橋極限承載能力的關鍵。

本次分析的重點為中間鋼塔的極限承載力，所以忽略邊塔混凝土的材料非線性狀態，僅僅考慮中塔鋼材的材料非線性，假定邊混凝土橋塔不會因為達到極限承載力而退出工作。由于本次計入中塔的雙重非線性，所以不考慮由于焊接殘余應力帶來的材料強度折減。由于缺乏確定的統計規律，忽略由于施工誤差造成的折減，這是因為：①施工誤差在全橋所有構件均存在，無法定量評估；②極限承載力分析旨在從設計的角度，考慮理想設計狀態下的薄弱截面或構件的薄弱部位，以便有針對性地進行補強，達到全橋安全系數基本一致的目的，而不是計算由于施工誤差對結構造成的損傷。因此，可以不計入施工誤差的影響。

2 全橋計算模型和荷載工況

本文采用大型通用有限元軟件建模，計算中考慮了幾何和材料雙重非線性，利用有限元軟件ANSYS，中間鋼塔采用可以考慮大變形的4節點平面殼單元，其他部分采用桿系模型，懸索橋全橋模型見圖2。

圖2 懸索橋總體模型

除了材料非線性外，懸索橋的幾何非線性主要考慮由于垂度效應、梁柱效應、大變形產生的幾何非線性，通過考慮幾何非線性和材料非線性的雙線性模型分析，對橋塔的極限承載能力進行評估[3]。考察構件在平截面假定失效情況下的工作模式、結構的極限荷載，以及安全系數，尋找中間橋塔的破壞模式和倒塌模式以判斷橋塔的薄弱部位，通過橋塔局部屈曲和整體屈曲模態，確定截面破壞的形式，為截面進行分類提供依據。

因為中間人字形鋼塔是本次分析的重點，所以進行精細殼元建模，其他部位采用桿系單元組建全橋建模。橋塔構造采用三維強非線性板殼單元(Solid181)模擬，Solid181單元是ANSYS針對彈性殼元不足開發的高級單元，本單元特別適合于分析具有線性、大角度轉動和/或非線性大應變特性的應用問題，能夠模擬結構從線彈性到結構完全塑性的全過程；吊桿采用桿單元(Link8)模擬；鋼加勁梁和邊PC橋塔均采用三維梁單元(Beam4)進行模擬；主纜采用只受拉單元(Link10)模擬。中塔模型離散圖見圖3。

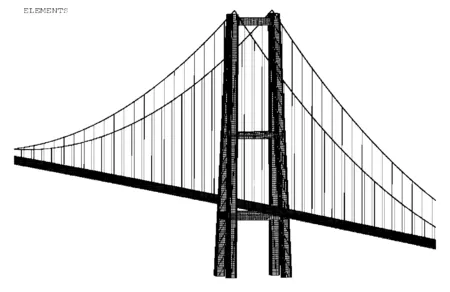
圖3 懸索橋中間鋼塔離散圖

隨著有限元計算軟件的普及，關于極限承載力分析的研究較多[4-5]，研究成果主要在加載方面有所差異，有的研究采用的是恒載和活載同時倍增的計算方法，有的采用的是恒載不變，活載單獨倍增的方法。本文認為均有道理，恒載和活載同時倍增，對于懸索橋受力分析更有意義，因為懸索橋的結構剛度很大一部分是來自于重力剛度，如果恒載倍增，可以改善主纜的應力剛度，進而更能保證結構在極限狀態下的計算收斂，缺點是，在設計階段，由于主纜的施工和受力狀態可以較好地保證，因此主纜的安全系數往往在2.5～3之間，然而橋塔等其他構件的安全系數均大于這個數值，于是很難捕捉到橋塔的失效。恒載不變，單獨倍增活載，可以得到一些偏載工況下的主塔極限承載力，缺點是由于主纜的重力剛度增加不多，所以結構變形偏大。再綜合考慮雙重極限承載力分析主要是尋找全橋結構的薄弱點，因此，本文綜合考慮了2種荷載倍增的方法進行計算。由于不需要重新建模，計算成本增加并不多。

計算中采用增量迭代的牛頓-拉斐遜方法，屈服判斷采用von Mises屈服準則，不考慮恒載和活載同時倍增的模式加載，而是采用表1中9種模式加載。

表1 加載模式

續表1

3 薄壁結構分析方法

只有通過極限狀態的分析和對倒塌過程的模擬，才可以反映構件的整體和局部失效過程及更好地反映他們之間的先后關系[6]。取圖4所示的簡單薄壁結構為例，利用虛功原理建立結構達到承載能力極限狀態時的平衡方程見式(1)。

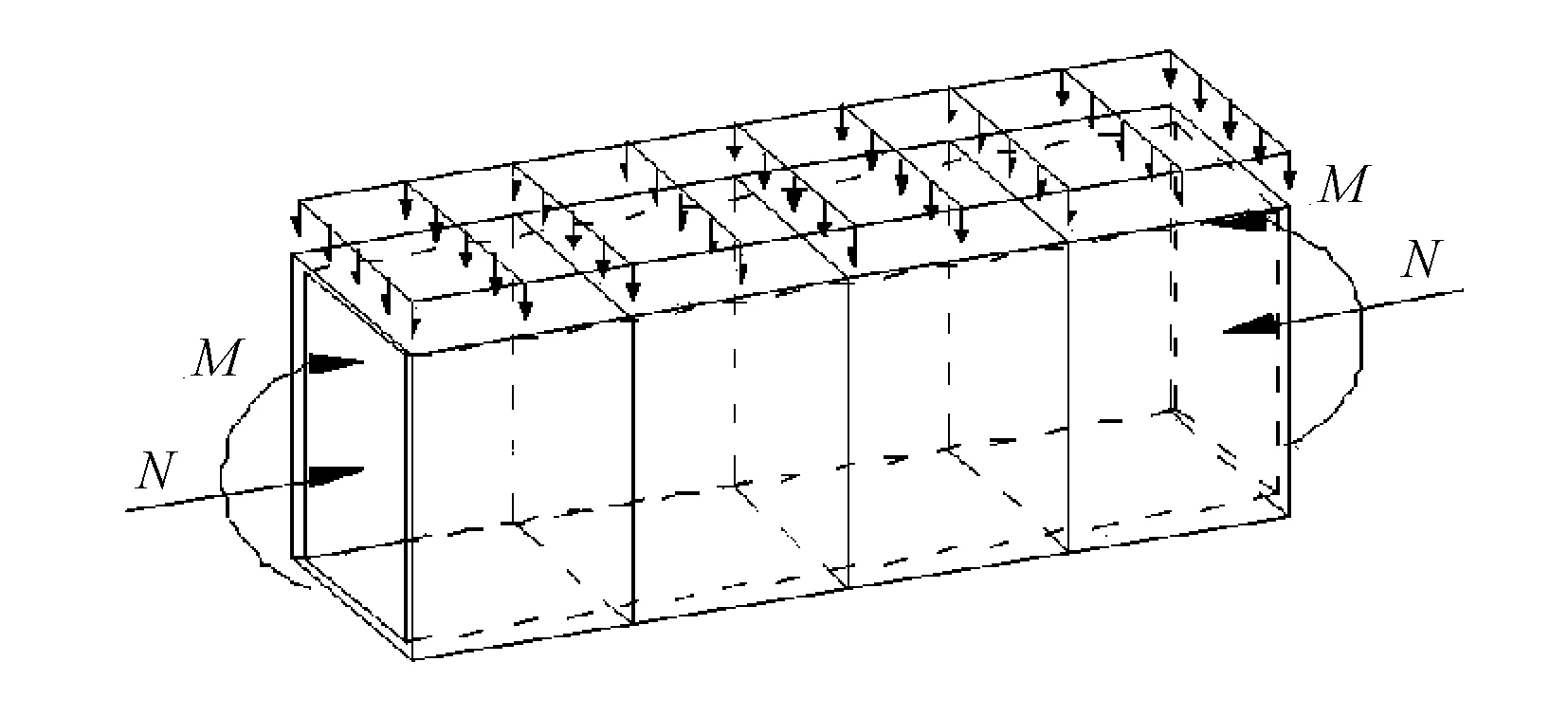
圖4 軸力和彎矩作用下的簡單薄壁結構

(1)

式中：ψ為內力和外力的矢量總和；f1為所有荷載列陣；dδ為虛位移，dε為虛應變。如果對應于一般的線彈性關系，則

dψ=(K0+Kσ+KL)dδ=KTdδ

(2)

式中：K0為小位移的線性剛度矩陣；Kσ為幾何剛度矩陣；KL為大位移矩陣；KT為切線剛度矩陣。

平衡微分方程中包含了幾何矩陣和大位移矩陣，可見對于薄壁結構而言數學上的困難是由于幾何非線性和材料非線性及整體和局部屈曲帶來的，往往需要忽略其中一項或者幾項來近似得到工程師想要的結果。線性屈曲、非線性屈曲、雙非線性分析是根據對式(2)的簡化程度不同而定義的。

線性屈曲分析忽略了大位移矩陣，理論上假定當外荷載達到結構的臨界荷載時，雖然應力水平并不高，但是在小的擾動之下，結構便會發生突然的彎曲而進入不平衡狀態，盡管荷載不變，結構的變形卻繼續增加，最終達到破壞。計算時假定結構在加載的各個階段總認為結構在未加載的原始位置上產生平衡，當屈曲發生時，結構突然跳到另一個平衡位置。線性屈曲分析，是一個廣義特征值問題，而結構的平衡實際上是在結構發生變形后達到的。

因此實際結構從一開始就出現了幾何非線性的特性，要進行非線性屈曲分析。非線性屈曲如圖5中曲線所示，當荷載比例因子增加時λ-δ曲線是非線性的，最終達到極限荷載失去承載力。在加載過程中，結構在不斷更新的位形上達到平衡，當達到極限荷載時，結構失去承載力。對應的平衡方程為

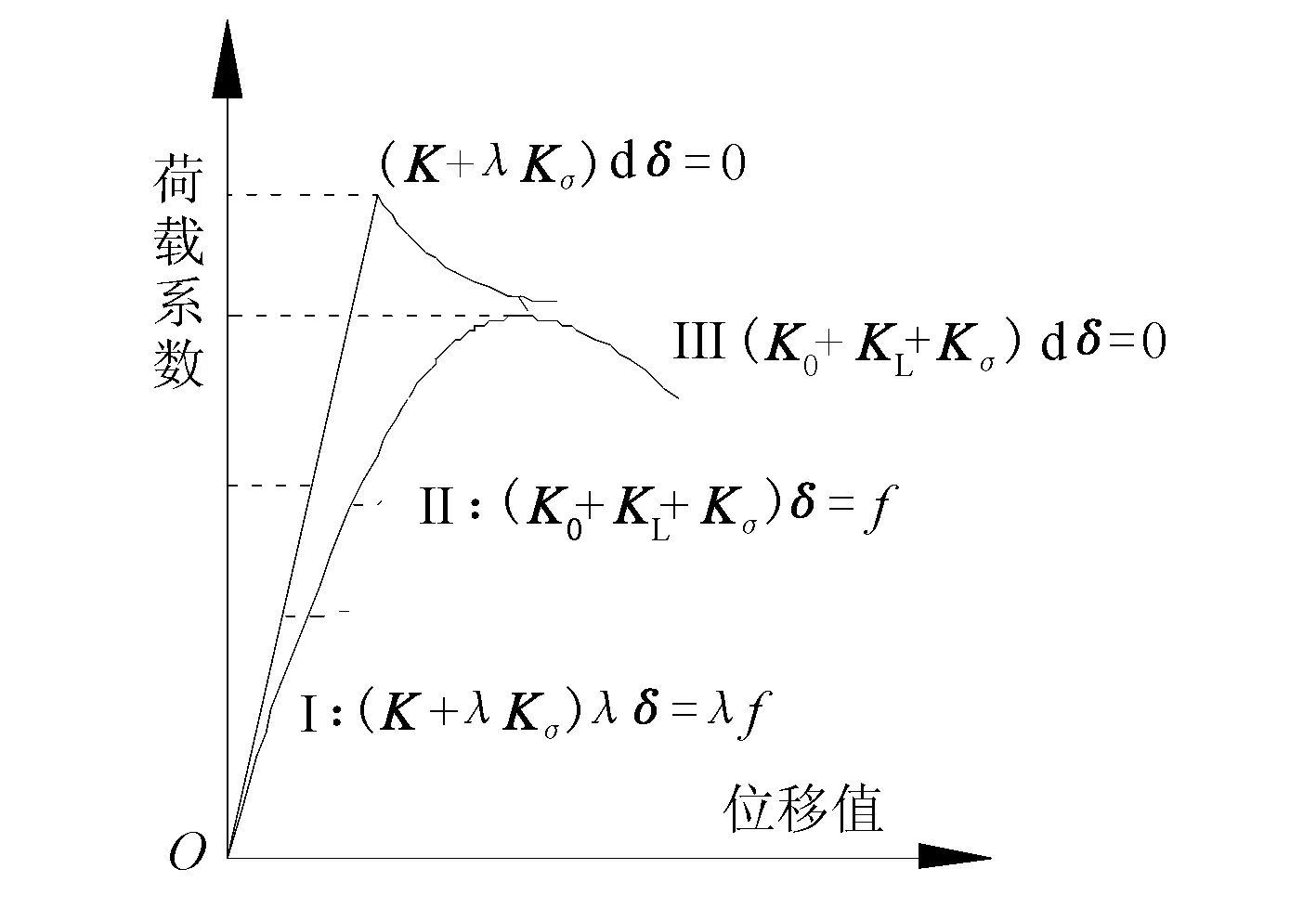
圖5 考慮幾何非線性的荷載曲線

(K0+Kσ+KL)dδ=0

(3)

上述方程式是按照材料完全彈性的條件建立的，求解過程中僅考慮了各種幾何非線性的影響。實際結構中，在進行非線性屈曲分析時，隨著材料應力的增加，應力-應變不再是線性關系，而符合如下的非線性方程

σ=[Dε(ε-ε0)]+σ0

(4)

式中：Dε為結構位移矩陣；ε0為初應變矩陣；σ0為初應力矩陣。

當應力達到一定水平，雖然分支點失穩還沒出現，但構件的邊緣纖維開始屈服，當荷載繼續增加，由于塑性區的向外擴展，結構內部纖維的屈服發展加快，最終形成塑性鉸導致結構破壞。于是在非線性屈曲中，便出現了第二類穩定問題，即極值點失穩。

4 中間鋼塔極限承載力分析

極值點失穩見圖5所示。整個加載過程中的薄壁結構的λ(滿載比例因子)-δ曲線可以分為3個階段，I)線性階段，即沒有局部的屈曲也沒有材料非線性；II)非線性階段，材料進入非線性或者發生屈曲；III)失效后階段，塑性鉸形成，結構喪失承載能力。對于薄壁構件進行材料和幾何雙重非線性分析時，無論是失穩破壞還是強度破壞，都將導致大變形和塑性區的發展，因此從破壞后的狀態無法識別破壞的產生原因。

通過觀察構件屈曲和材料屈服先后關系可將塑性鉸按形成誘因分為3種類型。類型一、屈曲誘因型：當達到屈曲失穩荷載時，邊緣纖維的應變還沒有達到屈服強度；屈曲導致的局部大變形和大應變，最終導致材料屈服形成塑性鉸。類型二、臨界類型：邊緣纖維進入屈服時恰好達到了結構的屈曲荷載。類型三、屈服誘因型：部分邊緣纖維首先屈服，屈服逐漸擴展，最后全截面達到屈服狀態，形成塑性鉸。

經計算得到中間鋼塔各個工況荷載安全系數見表2。

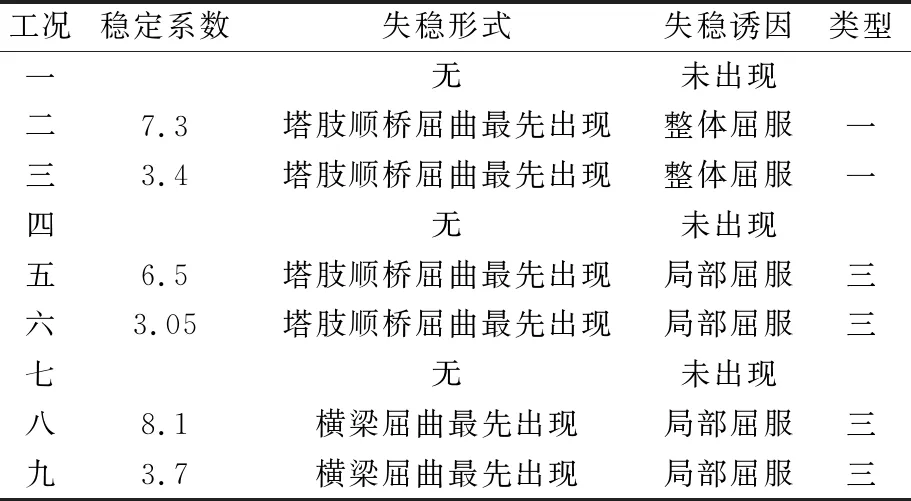
表2 懸索橋中塔失穩形式和穩定系數

由表2可知，安全系數最小的是工況六，整體失效模式為由于單跨荷載的增加，橋塔受到不平衡彎矩的作用，在這個作用下，塔肢單側的外側鋼板受到很大的面內壓力，最終局部板段攜帶著內部加勁肋一起變形，首先形成局部屈曲進而發展成為截面塑性鉸，導致構件最終喪失了承載力。目前規范中并未就極限荷載的穩定系數給出界定，主要是因為正常使用和承載能力極限狀態均不允許結構出現以致倒塌的受力狀態，或者說目前不能以此水準作為設計的依據。因此，關于合理的極限狀態的穩定系數規范值尚無確定標準。本文未對結構失效后荷載曲線的下降段進行分析，作為一般的土木結構，結構屈曲后失效模式不太重要，關于此時結構的力學行為，有待進一步研究。

雙重非線性極限承載力分析的安全系數常常比彈性屈曲分析得到的安全系數低的多，這主要是因為在線彈性分析中，材料非線性的影響往往是被忽略的。另外，彈性屈曲分析是利用幾何剛度矩陣進行的特征值運算，并不能考慮結構在發生初始變形后的剛度改變，比如局部屈曲的影響和P-Δ效應的影響等，因此會出現彈性屈曲分析安全系數較高的問題。到目前為止，對于一個構件來說相對容易分析，但是對于懸索橋這種由多種單元組成的結構復雜的體系，還缺少研究專門論述這2種屈曲安全系數之間的定性關系。

5 結論

本文以薄壁結構極限承載力的計算原理為基礎，分析了三塔兩主跨懸索橋中間人字形鋼塔的極限承載力。利用有限元軟件ANSYS建立全殼單元的中間鋼塔并用桿系建立其他構件的全橋空間有限元模型，考慮恒載和活載分別倍增的方式，采用考慮雙非線性的增量迭代牛頓-拉斐遜方法計算中間鋼塔的極限承載力。主要結論如下。

1) 計算得到各種工況下懸索橋中間鋼塔極限承載力穩定系數，并通過對失效模式和失效誘因的分析，找到結構需要加強的薄弱部位和失效模式，為結構的優化設計提供依據。

2) 采用通過活載單獨倍增的方式對結構外力的安全系數進行模擬，進一步分析結構的薄弱環節；恒載和活載一起倍增的方式計算結構的安全系數，中間鋼塔失穩時，主纜等其他傳力構件也幾乎達到極限強度，從一定意義上說明全橋強度配置合理。

3) 橫向風荷載作用下結構失穩是由于上橫梁下緣處塔柱內側壁板達到屈服強度開始的，屬于屈服誘因形成的塑性鉸。加大屈服開始部位的壁厚可以有效減小局部應力，提高整體結構的運營安全系數，可以通過較小的代價實現大幅提高結構安全系數的目的。

結構失穩后的強化階段的力學行為，以及雙重非線性極限承載力安全系數和彈性屈曲安全系數之間的定性的關系，有待進一步研究。