矩形水池底板基床系數(shù)的探討

胡慶 俞靖端

中國(guó)市政工程中南設(shè)計(jì)研究總院有限公司 武漢430010

引言

文克爾地基模式是目前較為實(shí)用的水池-地基共同作用的主要模擬方法之一。其假定地基單位面積上所受的壓力P與地基的豎向位移y成正比：P＝Ky，式中K為基床系數(shù)，即地基上某點(diǎn)的沉降只與該點(diǎn)土作用的壓力有關(guān)。文克爾地基模式下，合理地選擇基床系數(shù)K值對(duì)計(jì)算成果的精確性和可靠性有著重要意義。

基于文克爾假定的水池有限元計(jì)算建模中，通常在底板底部設(shè)置豎向彈簧，并在底板四個(gè)角點(diǎn)施加水平位移約束，作為水池結(jié)構(gòu)的邊界條件。而文獻(xiàn)［1］通過(guò)比較分析得出：在底板四個(gè)角點(diǎn)施加水平位移約束是不合理的，而在底板四個(gè)角點(diǎn)施加不動(dòng)鉸支座的邊界條件是合理的，能反映底板與地基變形的實(shí)際分布趨勢(shì)。

然而在底板四個(gè)角點(diǎn)施加不動(dòng)鉸支座，會(huì)引起四角應(yīng)力集中，導(dǎo)致底板、壁板局部?jī)?nèi)力特征失真。在底板設(shè)置豎向彈簧的基礎(chǔ)上，同時(shí)在底板設(shè)置水平彈簧從而限制結(jié)構(gòu)的水平向位移，從常理上更貼合實(shí)際。本文對(duì)基床系數(shù)的取值、矩形水池在不同邊界條件下的有限元分析作相應(yīng)探討。

1 基床系數(shù)的取值

1.1 垂直基床系數(shù)取值

根據(jù)《巖土工程勘察規(guī)范》（GB 50021—2001（2009））［2］中第10.2.6 條，豎向基床系數(shù)Kv可根據(jù)平板荷載試驗(yàn)（K30 法）按下式計(jì)算：

式中：p為p-s曲線線性段壓力；s為p對(duì)應(yīng)的沉降量。

K30平板載荷試驗(yàn)是用直徑為30cm的荷載板測(cè)定下沉量為1.25mm時(shí)基床系數(shù)的試驗(yàn)方法。

在建筑及市政行業(yè)工程建設(shè)的地勘報(bào)告中，通常不提供巖土的基床系數(shù)。設(shè)計(jì)人員往往通過(guò)規(guī)范或手冊(cè)來(lái)查詢基床系數(shù)經(jīng)驗(yàn)值，然而規(guī)范或手冊(cè)中的基床系數(shù)經(jīng)驗(yàn)值僅有大致范圍，設(shè)計(jì)人員只能自行取值，同種巖土基床系數(shù)經(jīng)驗(yàn)值范圍較大，會(huì)造成較大偏差，從而影響結(jié)構(gòu)的計(jì)算精度。

地勘報(bào)告中一般都提供巖土計(jì)算地基沉降的參數(shù)壓縮模量（Es）。根據(jù)建筑地基基礎(chǔ)設(shè)計(jì)規(guī)范（GB 50007—2011）［2］中第5.3.5 條，地基變形量按下式計(jì)算：

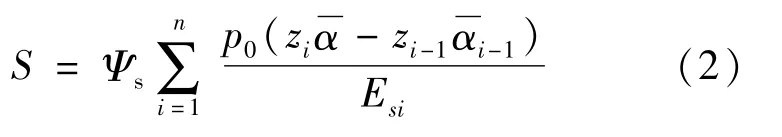
式中：s為沉降量（mm）；Ψs為沉降計(jì)算經(jīng)驗(yàn)系數(shù)；n為地基變形計(jì)算深度范圍內(nèi)所劃分的土層數(shù)；P0為相應(yīng)于作用的準(zhǔn)永久組合時(shí)基礎(chǔ)底面處的附加壓力（kPa）；Esi為基礎(chǔ)底面下第i層土的壓縮模量（MPa）；zi、zi-1為基礎(chǔ)底面至第i層土、第i-1 層土底面的距離（m）；為基礎(chǔ)底面計(jì)算點(diǎn)至第i層土、第i-1 層土底面范圍內(nèi)平均附加應(yīng)力系數(shù)。

根據(jù)式（1）、式（2）及K30 法的已知沉降量，經(jīng)驗(yàn)系數(shù)Ψs取1，巖土壓縮層厚取5 倍的壓板直徑為1.5m，即可解出巖土垂直基床系數(shù)Kv。根據(jù)多項(xiàng)實(shí)際工程的地勘報(bào)告中巖土數(shù)據(jù)，選取了其中較為典型的五種巖土，計(jì)算得出基床系數(shù)Kv見表1。其中垂直基床系數(shù)經(jīng)驗(yàn)值Kv摘自《城市軌道交通巖土工程勘察規(guī)范》（GB 50307—2012）［4］中附錄H。

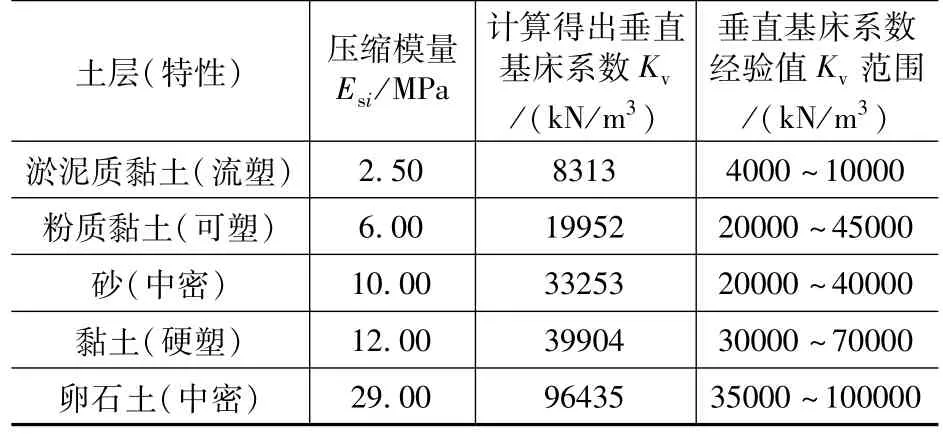
表1 計(jì)算基床系數(shù)與經(jīng)驗(yàn)基床系數(shù)的比較Tab.1 Comparison between calculated coefficient and empirical coefficient of subgrade bed

根據(jù)表1 可知，通過(guò)規(guī)范中的基床系數(shù)原位測(cè)試試驗(yàn)方法結(jié)合沉降計(jì)算公式，體現(xiàn)了基床系數(shù)與壓縮模量Es（室內(nèi)試驗(yàn)結(jié)果）的正向關(guān)系，在一定條件下基床系數(shù)Kv＝3.3Es，雖未考慮地區(qū)經(jīng)驗(yàn)因素，但得出的垂直基床系數(shù)Kv在經(jīng)驗(yàn)值范圍內(nèi)，其取值較為合理。

1.2 水平基床系數(shù)取值

在均勻土層中，正常固結(jié)土，由于土在不同應(yīng)力水平下的變形能力也不同，如圖1 所示，豎向荷載作用下，圍壓為σcx（σcy＝σcx），而到了水平方向，圍壓則變成了σcz，一般來(lái)說(shuō)σcx、σcy要比σcz小，較高側(cè)向壓力情況下的土應(yīng)該更強(qiáng)一些，從這個(gè)角度出發(fā)，同一位置，豎向與水平向受荷載深度一樣的土的水平基床系數(shù)Kh高于垂直基床系數(shù)Kv。

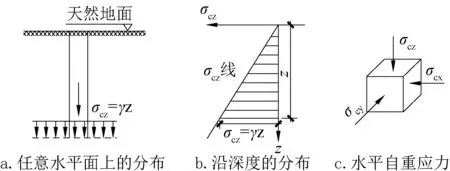
圖1 均質(zhì)土中豎向自重應(yīng)力Fig.1 Vertical dead weight stress in homogeneous soil

據(jù)規(guī)范［4］提供的基床系數(shù)經(jīng)驗(yàn)值，其80%巖土Kh／Kv比值分布在1～1.2 范圍，考慮到作為邊界條件Kh取值要求精度不高，故取Kh＝Kv。

2 矩形水池有限元分析

2.1 水池模型算例基本參數(shù)

為便于分析比較，水池模型的尺寸、構(gòu)件尺寸及荷載均與文獻(xiàn)［1］相同，幾何尺寸為L(zhǎng)×B×H＝20 ×10 ×5（m），壁板厚度0.4m，底板厚度0.5m，壁板水平三角形荷載50kPa，底板均布荷載50kPa，板單元尺寸0.5m ×0.5m。水池透視圖及有限元模型如圖2 所示。計(jì)算結(jié)果取水壓工況，不考慮結(jié)構(gòu)自重。

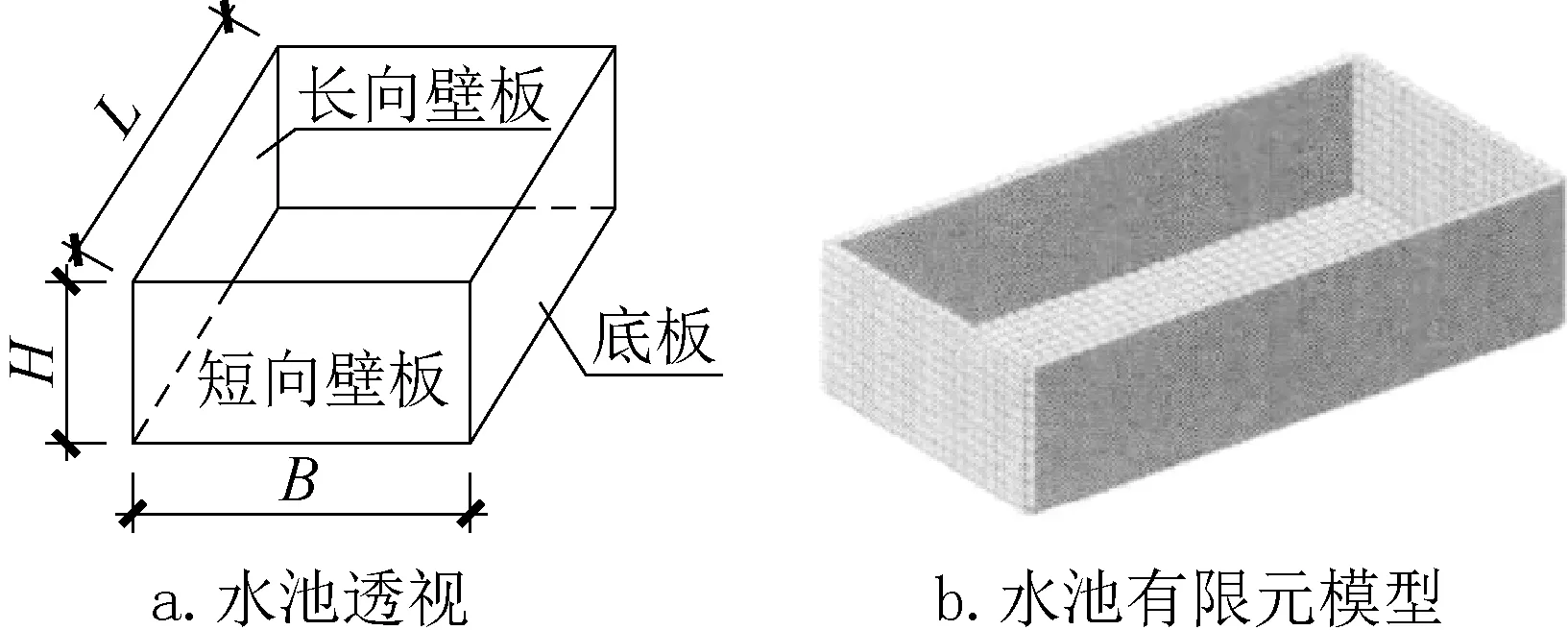
圖2 水池透視圖及有限元模型Fig.2 Pool perspective and finite element model

2.2 底板不同邊界條件的分析比較

底板三種約束簡(jiǎn)圖如圖3 所示。

圖3 底板三種約束簡(jiǎn)圖Fig.3 Three kinds of constraint diagrams of bottom plate

經(jīng)有限元分析計(jì)算不同邊界條件下壁板彎矩結(jié)果見表2。表2 結(jié)果驗(yàn)證了文獻(xiàn)［1］在底板四角僅設(shè)平面約束結(jié)果的不合理性，即角隅區(qū)彎矩Mx偏大，壁板豎向彎矩My偏小。底板設(shè)水平彈簧與底板四角設(shè)不動(dòng)鉸結(jié)果接近。不同邊界條件下壁板角隅區(qū)（長(zhǎng)向壁板在壁板轉(zhuǎn)角處約2m 寬范圍）彎矩分布如圖4 所示。圖4 結(jié)果表明，底板四角設(shè)不動(dòng)鉸情況下，其角隅區(qū)彎矩在底部突變從而影響了其周邊彎矩特征。底板設(shè)水平彈簧情況下，其角隅區(qū)彎矩特征更符合實(shí)際。

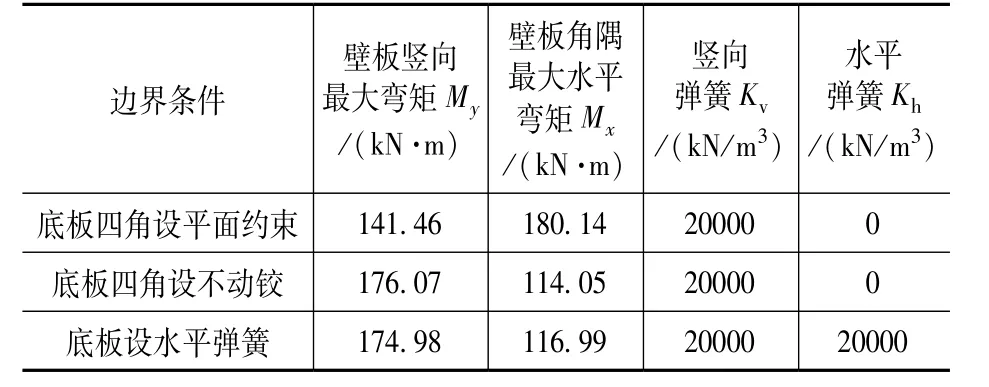
表2 不同邊界條件下壁板彎矩結(jié)果Tab.2 Bending moment under different boundry conditions

圖4 不同邊界條件下壁板角隅區(qū)彎矩分布（單位：kN·m） Fig.4 Bending moment distribution in the corner of panel under different boundary conditions（unit：kN·m）

兩種邊界條件下水池長(zhǎng)向中部橫斷面變形如圖5 所示。圖5 結(jié)果表明，底板四角設(shè)不動(dòng)鉸與底板設(shè)水平彈簧情況下結(jié)構(gòu)變形特征趨勢(shì)相同，底板變形均特征均為鍋底狀。

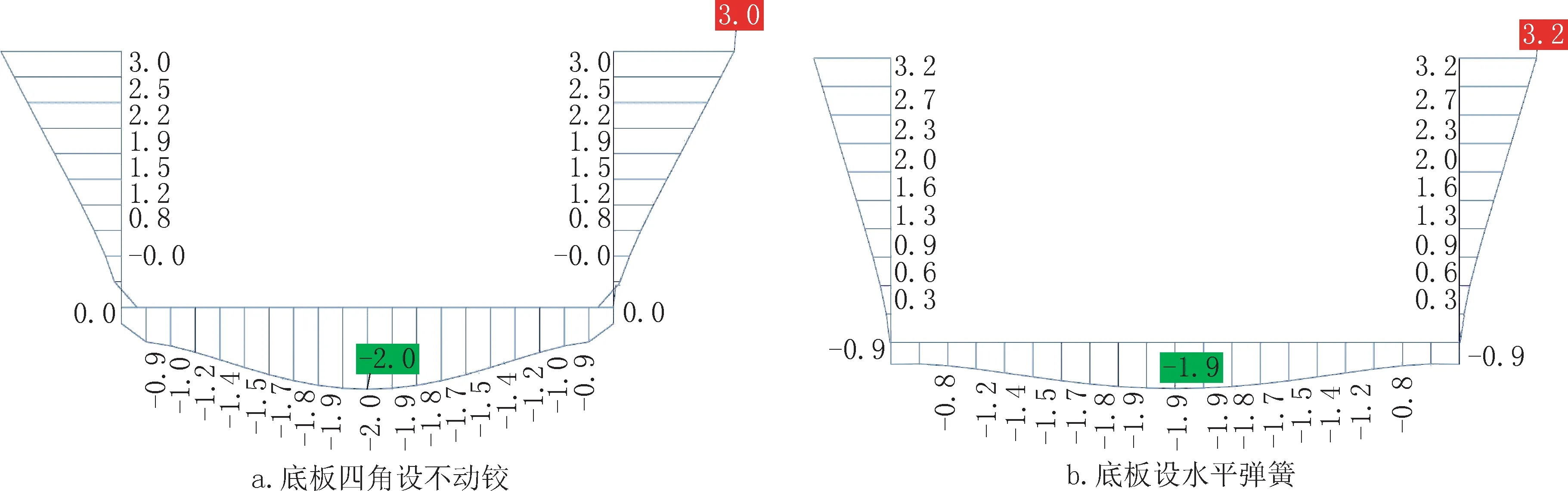
圖5 兩種邊界條件下水池長(zhǎng)向中部橫斷面變形（單位：mm）Fig.5 Deformation of longitudinal middle cross section of pool under two boundary conditions（unit：mm）

從以上分析比較情況來(lái)看，底板設(shè)水平彈簧作為邊界條件最為合理。

2.3 不同基床系數(shù)的分析比較

實(shí)際工程中，在軟土地基或不良地基情況下，地基變形較大，通常會(huì)對(duì)上部結(jié)構(gòu)產(chǎn)生較大影響。底板設(shè)水平彈簧作為邊界條件下，壁板彎矩隨基床系數(shù)變化趨勢(shì)如圖6所示。

從圖6 可知，My在基床系數(shù)在33000kN／m3以下時(shí)，其值隨基床系數(shù)增加而減小，其最大變化幅度約為10%，基床系數(shù)在33000kN／m3以上時(shí)，其值隨基床系數(shù)增加變化不大；Mx在基床系數(shù)在33000kN／m3以下時(shí)，其值隨基床系數(shù)增加而增加，其最大變化幅度約為21%，基床系數(shù)在33000kN／m3以上時(shí)，其值隨基床系數(shù)增加變化不大。

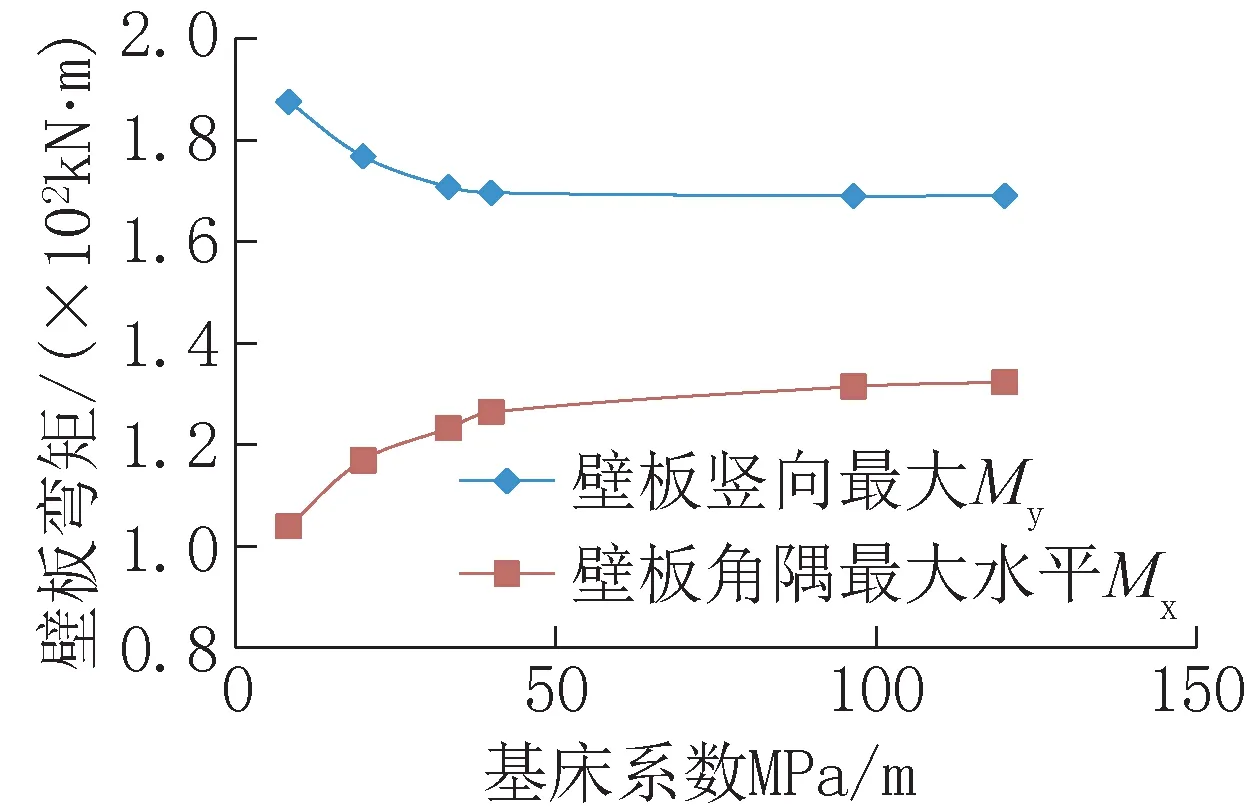
圖6 壁板彎矩隨基床系數(shù)變化趨勢(shì)Fig.6 Variation trend of bending moment of wall plate with subgrade coefficient

由此可見該敞口水池結(jié)構(gòu)，由于整體剛度不大，其對(duì)地基變形較為敏感。

3 相關(guān)問(wèn)題的討論

在第1節(jié)中通過(guò)理論計(jì)算，給出了用壓縮模量Es近似估算地基土基床系數(shù)的公式，即Kv＝3.3Es，雖然其計(jì)算數(shù)值與規(guī)范中給出的經(jīng)驗(yàn)值相近，但尚缺乏足夠的實(shí)際數(shù)據(jù)支撐，還有許多問(wèn)題值得進(jìn)一步探討。設(shè)計(jì)人員可根據(jù)地基土的類別、土的狀況、物理力學(xué)特性及其上部結(jié)構(gòu)特點(diǎn)酌情取值。

在基于文克爾假定的結(jié)構(gòu)有限元分析中對(duì)于矩形水池，底板四個(gè)角點(diǎn)施加不動(dòng)鉸支座及四個(gè)角點(diǎn)施加水平位移約束均完全限制了底板水平向位移，是設(shè)置水平彈簧的特殊情況，即當(dāng)水平彈簧無(wú)窮大時(shí)，完全限制了底板水平向位移。對(duì)于其他形式結(jié)構(gòu)的底板采用文克爾地基模型設(shè)置水平彈簧，可作類似分析。實(shí)際上對(duì)于圓形水池、管廊節(jié)點(diǎn)等整板基礎(chǔ)結(jié)構(gòu)，底板設(shè)置水平彈簧，其結(jié)構(gòu)內(nèi)力結(jié)果同樣合理，限于篇幅不再贅述。

4 結(jié)語(yǔ)

通過(guò)上述探討分析，可得如下結(jié)論：

1.用壓縮模量Es近似估算的地基土基床系數(shù)，其計(jì)算數(shù)值與規(guī)范中給出的經(jīng)驗(yàn)值相近，以此值作為基準(zhǔn)適當(dāng)考慮地基土的類別、土的狀況、物理力學(xué)特性及其上部結(jié)構(gòu)特點(diǎn)做一定修正用于有限元結(jié)構(gòu)分析是可行的。

2.基于文克爾假定，在矩形水池底板設(shè)置豎向彈簧基礎(chǔ)上，在底板設(shè)置水平彈簧替代四角平面約束或四角不動(dòng)鉸支座，該邊界條件貼合實(shí)際，水池結(jié)構(gòu)內(nèi)力計(jì)算結(jié)果合理，水池底板變形與實(shí)際相似。

3.尺寸較大（平面尺寸大于或等于L×B＝20m×10m）的鋼筋混凝土敞口水池結(jié)構(gòu)，由于其整體剛度不大，其結(jié)構(gòu)內(nèi)力對(duì)地基變形較為敏感。