基于因子分析的母線負荷異常數(shù)據(jù)辨識方法
文 旭,王 浩,黃 剛,顏 偉,張愛楓,趙國富,劉高群,曾星星
(1.國家電網(wǎng)公司西南分部,成都 610041;2.重慶大學 輸配電裝備及系統(tǒng)安全與新技術(shù)國家重點實驗室,重慶 400044;3.重慶電力交易中心有限公司, 重慶 400013)
高質(zhì)量的監(jiān)測數(shù)據(jù)對電網(wǎng)數(shù)字化發(fā)展具有重要現(xiàn)實意義[1],然而量測系統(tǒng)中母線負荷數(shù)據(jù)存在的各類異常影響了電力系統(tǒng)狀態(tài)估計[2]、負荷預測[3]等高級數(shù)字化應用。如何有效地辨識出母線負荷異常數(shù)據(jù),提高數(shù)據(jù)質(zhì)量一直是工程界和學術(shù)界關(guān)注的焦點[4]。
現(xiàn)有母線負荷異常數(shù)據(jù)辨識方法主要有3類:基于時間序列、基于聚類和基于時頻域變換的方法。基于時間序列的方法以負荷數(shù)據(jù)時序變化規(guī)律為基礎(chǔ),通過B樣條函數(shù)[5]、多項式[6]等基函數(shù)將樣本中的部分節(jié)點擬合成一條光滑曲線;然后在該光滑曲線上下劃定時序負荷數(shù)據(jù)的正常波動范圍,將超出該范圍的負荷數(shù)據(jù)辨識為異常數(shù)據(jù)。該類方法過分依賴序列的平滑特征,只對毛刺類異常較為有效。基于聚類的方法以負荷曲線簇為樣本,首先應用k-均值聚類算法[7-8]、模糊C均值聚類算法[9-11]等聚類方法將負荷曲線歸為幾類;然后各自提取其典型負荷曲線;最后將待辨識的負荷曲線與各典型負荷曲線對比,根據(jù)二者差異的大小判斷負荷曲線中是否含有異常數(shù)據(jù)。該類方法以歐氏距離或隸屬度作為負荷曲線類別劃分依據(jù),忽略了負荷曲線的形狀信息,可能導致曲線錯誤分類,進而影響異常數(shù)據(jù)辨識準確率。基于時頻域變換的方法中,文獻[12]通過離散傅里葉變換提取負荷曲線頻域日周期分量和周周期分量,將二者疊加并變換回時域生成典型負荷曲線;再通過比較待判定負荷曲線和典型曲線的差異來判定曲線異常與否。該方法僅憑負荷曲線日周期分量和周周期分量復原負荷曲線的特征,存在較大誤差。文獻[13-14]基于小波變換提取負荷曲線的時頻域特征,根據(jù)曲線頻域模極大值為主要特征辨識時域內(nèi)的負荷數(shù)據(jù)突變點,此類方法著重于異常數(shù)據(jù)的突變特征,僅對于毛刺異常數(shù)據(jù)的辨識較為有效。
綜上所述,現(xiàn)有母線負荷辨識方法存在適應性差、對數(shù)據(jù)異常特征利用不充分問題。據(jù)此,筆者基于母線負荷數(shù)據(jù)現(xiàn)狀剖析了異常數(shù)據(jù)的基本特征,闡明了因子分析應用于母線負荷異常數(shù)據(jù)辨識的基本原理,提出了基于因子分析的母線負荷異常數(shù)據(jù)辨識方法。該方法的核心包括:1)引入因子分析將母線負荷曲線分解為表征曲線正常時序變化規(guī)律的基本分量和表征曲線數(shù)據(jù)異常或隨機波動特征的隨機分量;2)基于負荷曲線隨機分量給出了異常數(shù)據(jù)辨識的3σ判定準則。
1 母線負荷異常數(shù)據(jù)基本特征剖析
電力系統(tǒng)母線負荷是大量終端負荷的總和,而各類終端負荷一天之內(nèi)用電模式相對固定,母線負荷自然也會表現(xiàn)出某種相對穩(wěn)定的日周期性。如圖1所示,110 kV母線的終端負荷為工商、市政、居民等多個類別終端負荷的總和,一天之內(nèi)負荷平穩(wěn)波動較小;而10 kV母線終端負荷大多僅包含居民負荷,呈現(xiàn)出顯著的雙峰特性。
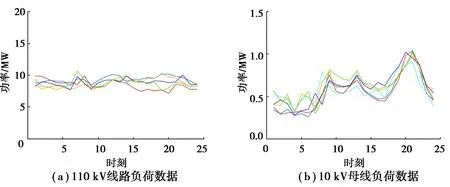
圖1 不同電壓等級的母線負荷數(shù)據(jù)Fig. 1 Bus load data of different voltage levels
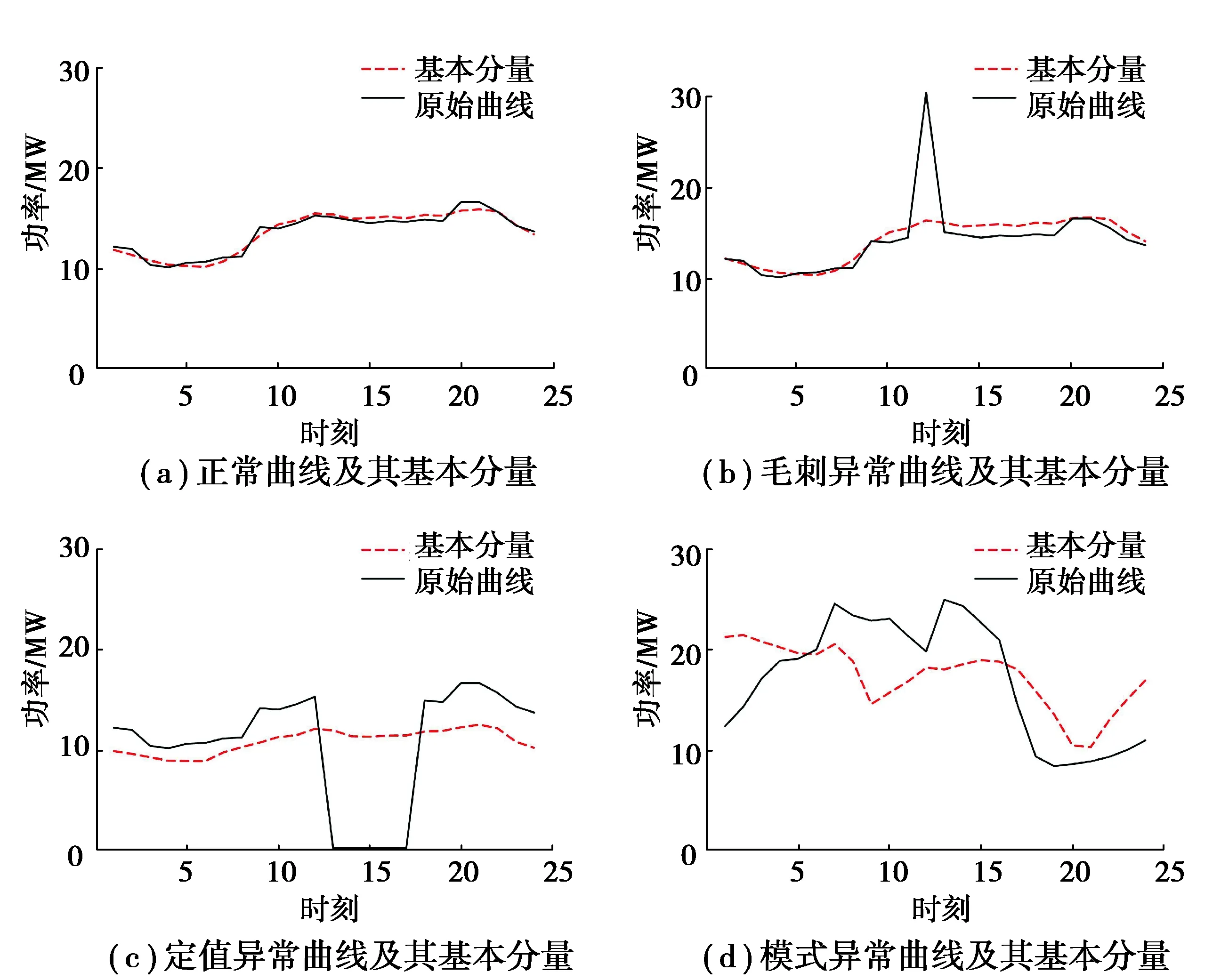
實際量測系統(tǒng)采集到的母線負荷除正常負荷數(shù)據(jù)外,通常還存在3類異常數(shù)據(jù):
1)毛刺異常數(shù)據(jù)。如圖2(b)所示,單個時刻或少數(shù)時刻負荷數(shù)據(jù)出現(xiàn)大幅度突變的異常數(shù)據(jù),該類異常數(shù)據(jù)多來源于數(shù)據(jù)采集、傳輸、儲存等各環(huán)節(jié)中的隨機干擾。
2)定值異常數(shù)據(jù)。如圖2(c)所示,在某時間段連續(xù)不變的異常數(shù)據(jù),該類異常數(shù)據(jù)多來源于量測系統(tǒng)故障。
3)模式異常數(shù)據(jù):如圖2(d)所示,與正常日負荷變化模式相比有顯著不同時序變化規(guī)律,該類異常數(shù)據(jù)多來源于電力系統(tǒng)故障。
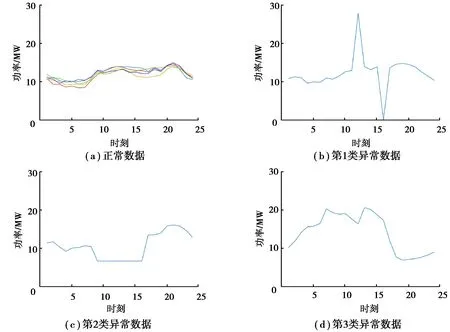
圖2 110 kV母線正常負荷曲線與異常負荷曲線Fig. 2 Normal and abnormal load curves of 110 kV bus
2 基于因子分析的母線負荷異常數(shù)據(jù)辨識原理
2.1 因子分析的基本原理
因子分析是一種依據(jù)變量間相關(guān)性將多維變量歸結(jié)為少數(shù)公共因子表示,然后加以分析處理的多維變量統(tǒng)計分析方法[15-16]。其基本思想是將原始變量分解為兩部分:一部分是公共因子的線性組合,濃縮表示了原始變量中的絕大部分信息;另一部分是與公共因子無關(guān)的特殊因子,反映了公共因子線性組合與原始變量間的差距。因子分析在統(tǒng)計分析中有許多應用,例如對樣本變量進行因子分析,提取出反映變量主要特征的公共因子,進而指導樣本分類處理[16]。
p維變量x=[x1,…,xi,…,xp]T的因子分析模型為
x=Af+ε。
(1)
或記為
(2)
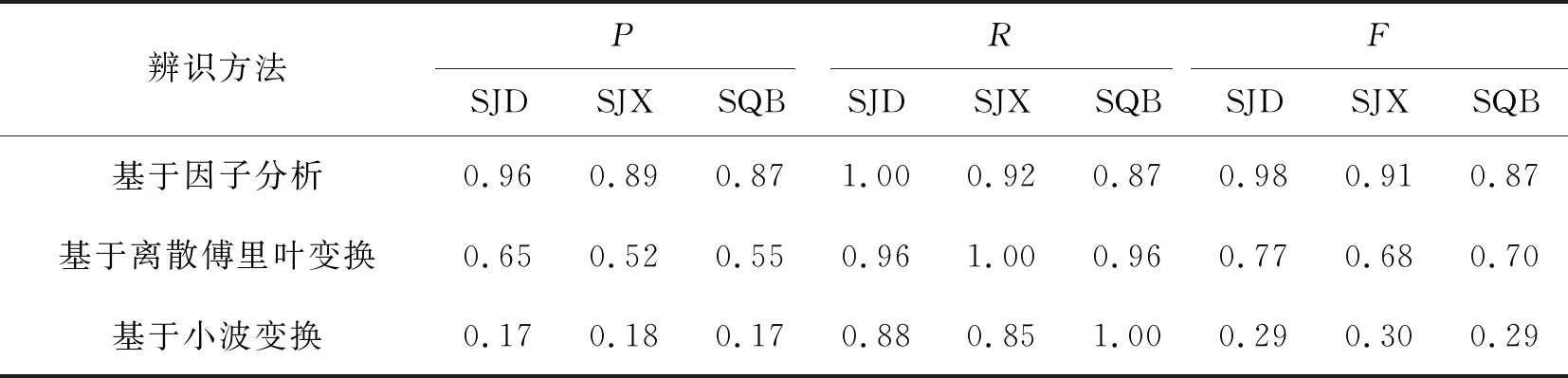
式中:f=[f1,f2,…,fm]T即為提取的公共因子向量,代表了原始變量中不可直接觀測但客觀存在的m(m 注意上述因子分析模型對各變量做了如下假設(shè): 1)公共因子向量f的協(xié)方差矩陣滿足covf=Em(Em為m階單位對角矩陣),即公共因子向量各分量間相互獨立,且各分量方差為1。 2)公共因子向量f與特殊因子向量ε的協(xié)方差矩陣滿足cov(f,ε)=0,即公共因子與特殊因子相互獨立。 3)特殊因子間相互獨立,特殊因子向量ε的協(xié)方差矩陣滿足 (3) 對多維變量x建立因子分析模型的關(guān)鍵在于求解因子載荷矩陣A和公共因子向量f。借鑒文獻[16]對上述2個參數(shù)進行估計。 因子載荷矩陣A的估計采用主成分法,其步驟如下: 1)為消除變量量綱不同的影響,對含n個p維變量的樣本Xp×n=[x1,x2,…,xn]進行標準化。標準化后,各變量的均值為0,方差為1。為表達方便標準化后的變量仍然用X表示,其各元素為 (4) 2)求樣本的協(xié)方差矩陣S,其各元素為 (5) (6) 其中參數(shù)m由公共因子的累積方差貢獻率[16]確定,即 (7) 一般認為,當前m個公共因子的累積方差貢獻率超過85%時,可認為前m個公共因子的線性組合基本上能夠還原原始變量信息。 公共因子向量f,即原始變量在公共因子上的具體得分可通過回歸法估計得到 (8) (9) 綜上所述即完成多維變量X因子分析模型的參數(shù)估計。 終端負荷的用電模式相對固定,母線負荷的時序變化規(guī)律具有明顯日周期性,因此正常的母線負荷曲線可視作反映日周期性時序變化規(guī)律的基本分量和反映負荷隨機波動特性的隨機分量的疊加,而含有異常數(shù)據(jù)的負荷曲線在此基礎(chǔ)上還疊加了背離正常時序變化規(guī)律的異常特征。 考慮到母線負荷曲線各時刻負荷數(shù)據(jù)間存在明顯相關(guān)性[17](如深夜至凌晨的用電低谷期負荷水平較低,而上午10時左右和晚上20時左右的用電高峰期負荷水平較高),因此可通過因子分析將母線負荷曲線樣本分解為公共因子的線性組合和特殊因子兩部分。在可合理假設(shè)樣本中只含有少量的異常曲線基礎(chǔ)上,濃縮表示各負荷曲線絕大多數(shù)信息的公共因子線性組合基本上表征了曲線正常時序變化規(guī)律,可視作曲線的基本分量;而反映公共因子線性組合和原始曲線差距的特殊因子則表征了曲線數(shù)據(jù)異常或隨機波動特征,可視作曲線的隨機分量。 經(jīng)因子分析得到表征負荷曲線數(shù)據(jù)異常或隨機波動特征的隨機分量后,通過檢測曲線隨機分量中是否含有異常特征,即可實現(xiàn)對異常負荷曲線的判別。 通常,母線負荷曲線中的異常數(shù)據(jù)占比低。但量測、通信設(shè)備故障則可能導致負荷數(shù)據(jù)出現(xiàn)長時段定值異常的情況,且異常占比較高。高占比異常數(shù)據(jù)將對負荷曲線基本分量提取造成較大干擾。不過此類異常特征明顯,可以較為容易地通過預篩選將此類異常的負荷曲線加以排除。而經(jīng)預篩選后的負荷曲線樣本中異常曲線占比很少,樣本異常數(shù)據(jù)含量低,對樣本進行因子分析提取基本分量時可忽略異常數(shù)據(jù)影響。將預篩選后的所有負荷曲線作為樣本,設(shè)含n條負荷曲線的樣本為 (10) 式中:xij為樣本中第j條負荷曲線第i時刻負荷值;p為負荷曲線的采樣頻率,取p=24。 基于因子分析的負荷曲線樣本基本分量和隨機分量的提取步驟如下: (11) 2)計算標準化負荷曲線樣本X的協(xié)方差矩陣S為 (12) 3)計算負荷曲線樣本協(xié)方差矩陣S的特征值λ1≥λ2≥…≥λp≥0和對應的單位正交特征向量γ1,γ2,…,γp。 (13) 5)對負荷曲線進行逆標準化變換后,可得負荷曲線的基本分量Xb和隨機分量Xr為 (14) 至此,基于因子分析的負荷曲線樣本基本分量與隨機分量的提取完成。 母線負荷的隨機波動來源于數(shù)據(jù)采集、傳輸及儲存等過程中的高斯噪聲,異常數(shù)據(jù)的產(chǎn)生是由于量測系統(tǒng)故障或者受到外界隨機干擾以及電力系統(tǒng)本身故障運行導致,因此正常母線負荷曲線各時刻隨機分量滿足正態(tài)分布,異常曲線則不然。據(jù)此,筆者提出了基于負荷曲線隨機分量的異常數(shù)據(jù)判定準則:若曲線各時刻負荷隨機分量滿足正態(tài)分布的拉依達(3σ)準則,即判定該數(shù)據(jù)正常,否則判定該數(shù)據(jù)異常。 下面對負荷曲線樣本隨機分量的正態(tài)分布參數(shù)進行估計,含n條負荷曲線的樣本隨機分量矩陣為 (15) (16) (17) 因此,母線負荷曲線隨機分量Xr不滿足下列關(guān)系的負荷數(shù)據(jù)即可判定為異常數(shù)據(jù),即 Xr-lower≤Xr≤Xr-upper。 (18) 所提基于因子分析的母線負荷異常數(shù)據(jù)辨識方法流程步驟如下: 4)根據(jù)式(14)取公共因子線性組合為樣本曲線基本分量Xb,取特殊因子為樣本曲線隨機分量Xr,并對二者進行逆標準化處理。 5)根據(jù)隨機分量的分布規(guī)律,按式(17)確定負荷曲線樣本隨機分量波動下限Xr-lower和波動上限Xr-upper。 6)將樣本曲線各時刻隨機分量xrij逐個與波動下限xr-lowerij和波動上限xr-upperij對比,判斷負荷數(shù)據(jù)xij是否異常。 上述步驟的流程圖如圖3所示。 圖3 基于因子分析的母線負荷異常數(shù)據(jù)辨識方法流程圖Fig. 3 Flow chart of bus load abnormal data identification method based on factor analysis 為驗證筆者所提方法的合理性和有效性,以重慶市某供電公司4條110 kV母線2015年1 h分辨率的負荷數(shù)據(jù)為樣本進行算例分析。原始數(shù)據(jù)基本信息如表1所示,負荷曲線簇繪制如圖4所示。 表1 4條110 kV母線負荷數(shù)據(jù)樣本 基于因子分析的異常負荷數(shù)據(jù)辨識方法有兩點假設(shè):一是負荷曲線基本分量能表征負荷曲線的正常時序變化特征,與正常負荷曲線基本吻合;二是樣本中少量的異常數(shù)據(jù)對樣本基本分量提取的影響可忽略不計。現(xiàn)對上述兩點假設(shè)的合理性進行論證。 針對假設(shè)一,可對全正常曲線樣本進行因子分析,若全正常樣本提取的基本分量與各曲線有良好的吻合度,則可證實該假設(shè)成立。筆者引用均方根誤差(CRMSE)和絕對值誤差(CMAE)[18]2個指標對基本分量與樣本正常曲線的吻合程度進行定量分析,即 (19) (20) 以原始負荷數(shù)據(jù)樣本為基礎(chǔ),剔除樣本中異常負荷曲線,只保留符合一般時序變化規(guī)律的正常曲線,剔除異常曲線后正常曲線樣本基本信息如表2所示。 表2 剔除異常曲線后的正常數(shù)據(jù)樣本 根據(jù)式(19)(20)計算全正常曲線樣本基本分量與各樣本曲線均方根誤差(CRMSE)和絕對值誤差(CMAE),計算結(jié)果如表3所示。據(jù)表3可見各樣本CRMSE和CMAE值均不超過8%,表明基本分量與正常負荷曲線吻合程度高,即基本分量能表征負荷曲線的正常時序變化特征。 表3 正常曲線樣本與基本分量的相對誤差 針對假設(shè)二,需對含少量異常負荷曲線的樣本進行因子分析,若樣本基本分量和樣本中正常樣本曲線的吻合程度與全正常曲線樣本高度接近,則可判定假設(shè)成立。 排除異常數(shù)據(jù)占比大的DQ母線,以異常數(shù)據(jù)占比小的SJD、SJX、SQB 3條母線負荷曲線為樣本。同時為驗證異常數(shù)據(jù)比例增加時方法的魯棒性,在不改變異常數(shù)據(jù)占比較少(10%以內(nèi))的大前提下,適當增加樣本中異常數(shù)據(jù)的比例。增加異常數(shù)據(jù)比例后的母線負荷數(shù)據(jù)如表4所示。 表4 增加異常數(shù)據(jù)比例的母線負荷數(shù)據(jù) 依舊采用均方根誤差(CRMSE)和絕對值誤差(CMAE)來衡量含異常曲線樣本基本分量與樣本中正常曲線的吻合度,但因計算的是基本分量與正常曲線的吻合程度,計算誤差時要剔除樣本中的異常曲線。計算可得含異常曲線樣本基本分量與樣本中正常曲線的均方根誤差(CRMSE)和絕對值誤差(CMAE)如表5所示。可見各樣本基本分量與全正常曲線樣本高度接近,即證實少量異常數(shù)據(jù)對樣本基本分量提取的影響可忽略。 表5 含異常曲線樣本中基本分量與正常曲線的相對誤差 將110 kV SJD母線各類負荷曲線與其基本分量繪制如圖5所示。 圖5 110 kV SJD母線各類負荷曲線及其基本分量Fig. 5 Various load curves and basic components of 110 kV SJD bus 綜上所述,基于因子分析分解得到的基本分量與正常負荷曲線高度吻合,表征了負荷曲線的正常時序變化規(guī)律。且這一結(jié)論在樣本中含有少量異常曲線的條件下也成立。因此,通過隨機分量(基本分量與原始曲線的差距)來判斷曲線是否異常的方案是合理的。 將所提方法分別與基于傅里葉離散傅里葉變換和小波變換的母線負荷異常數(shù)據(jù)辨識方法進行對比,以驗證所提方法的有效性。 選取基于混淆矩陣[19]的精確率(precision,P)、召回率(recall,R)和F1(F)值為指標評估各方法辨識效果。以表4中SJD、SJX、SQB 3條母線負荷數(shù)據(jù)為樣本,分別基于因子分析、離散傅里葉變換和小波變換的3種辨識方法的辨識效果如表6所示。 表6 3種辨識方法的效果對比 由表6可知,筆者所提基于因子分析方法相比于傅里葉法和小波分析法在精確率和召回率上都有明顯優(yōu)勢,綜合評價指標F1值也明顯優(yōu)于其他兩種方法,具體而言,基于離散傅里葉變換的異常數(shù)據(jù)辨識方法僅提取了負荷曲線日周期分量和周周期分量,難以對原始負荷曲線進行精確復原,導致辨識精確率低,誤報情況嚴重,而基于小波變換的辨識方法側(cè)重于對突變點的檢測,能夠在一定程度上實現(xiàn)對毛刺異常數(shù)據(jù)的辨識。由于部分負荷的隨機擾動和突變點特征相似,小波變換方法極易將這種正常隨機擾動誤辨識為異常數(shù)據(jù),而筆者所提出基于因子分析的母線負荷異常數(shù)據(jù)辨識方法則能夠兼顧各類異常數(shù)據(jù)的情況,適應性較好。 綜上所述,基于因子分析的異常負荷數(shù)據(jù)辨識方法能夠有效地辨識出母線負荷的各類異常數(shù)據(jù),且所提方法優(yōu)于基于離散傅里葉變換和小波變換方法的辨識效果。 筆者以110 kV母線歷史負荷數(shù)據(jù)對所提方法進行了仿真分析,結(jié)果表明所提方法對110 kV母線負荷數(shù)據(jù)有良好的辨識效果。對于110 kV之下的10 kV母線負荷曲線由于其用電規(guī)律性相對較弱,可能不滿足所提方法的2個假設(shè)條件,故所提方法對110 kV以下母線負荷異常數(shù)據(jù)辨識的實用性有待深入研究。而對于110 kV以上電壓等級母線負荷異常數(shù)據(jù)辨識,一般而言,由于該電壓等級負荷更加集中,用戶用電行為規(guī)律性更強,更容易滿足所提方法的2個假設(shè)條件。據(jù)此,所提方法對110 kV以上電壓等級母線負荷異常數(shù)據(jù)辨識亦有效。 考慮傳統(tǒng)母線負荷異常數(shù)據(jù)辨識方法的局限性,提出了基于因子分析的母線負荷異常數(shù)據(jù)辨識方法,主要研究結(jié)論如下: 1)所提方法提取的母線負荷曲線基本分量表征了曲線的主要正常時序變化特征,且少量異常數(shù)據(jù)不影響負荷曲線基本分量的提取;母線負荷曲線的隨機分量表征了曲線的數(shù)據(jù)異常和隨機波動特征,可根據(jù)隨機分量波動是否越線判斷曲線是否含有異常數(shù)據(jù)。 2)所提方法關(guān)于負荷曲線基本分量能表征負荷曲線的基本時序變化特征且與正常負荷曲線基本吻合,以及樣本中少量異常數(shù)據(jù)對樣本基本分量提取的影響可忽略不計的假設(shè)均經(jīng)算例驗證合理。 3)所提方法能夠兼顧各類母線負荷異常數(shù)據(jù)的情況,有效地辨識出母線負荷異常數(shù)據(jù),適應性較好,且辨識效果優(yōu)于傳統(tǒng)的基于離散傅里葉變換和小波變換的方法。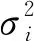
2.2 因子分析模型的參數(shù)估計

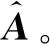
2.3 基于因子分析的母線負荷異常數(shù)據(jù)辨識方法機理
3 基于因子分析的母線負荷異常數(shù)據(jù)辨識方法
3.1 基于因子分析的負荷曲線基本分量和隨機分量的提取
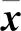
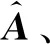
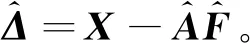
3.2 基于隨機分量的異常數(shù)據(jù)3σ判定準則
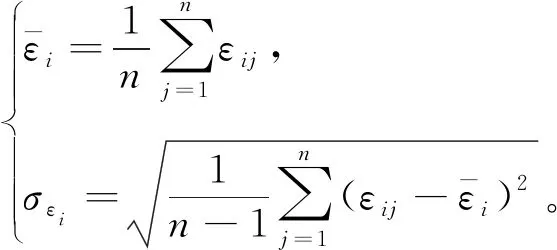
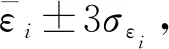
3.3 所提方法流程
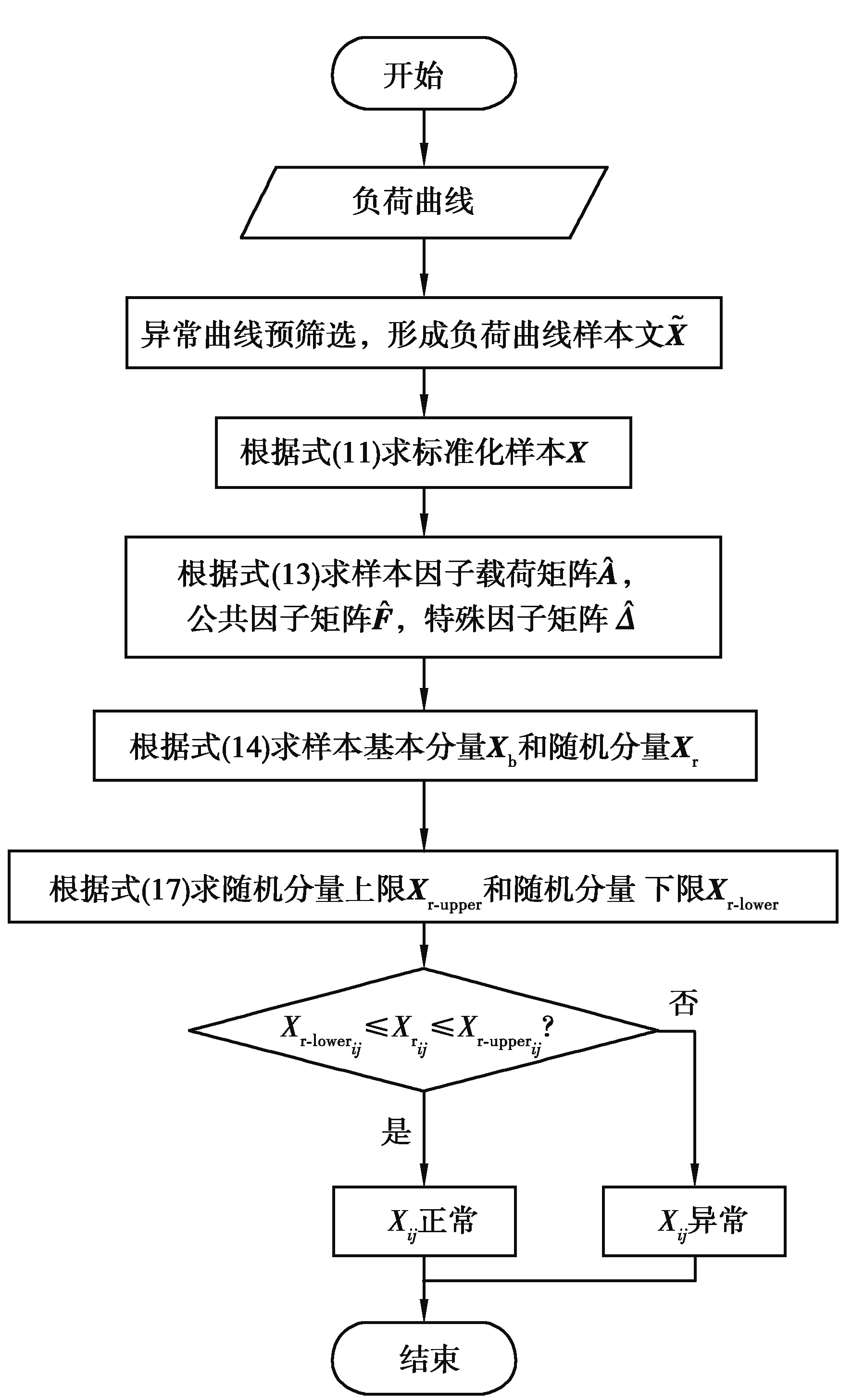
4 算例分析
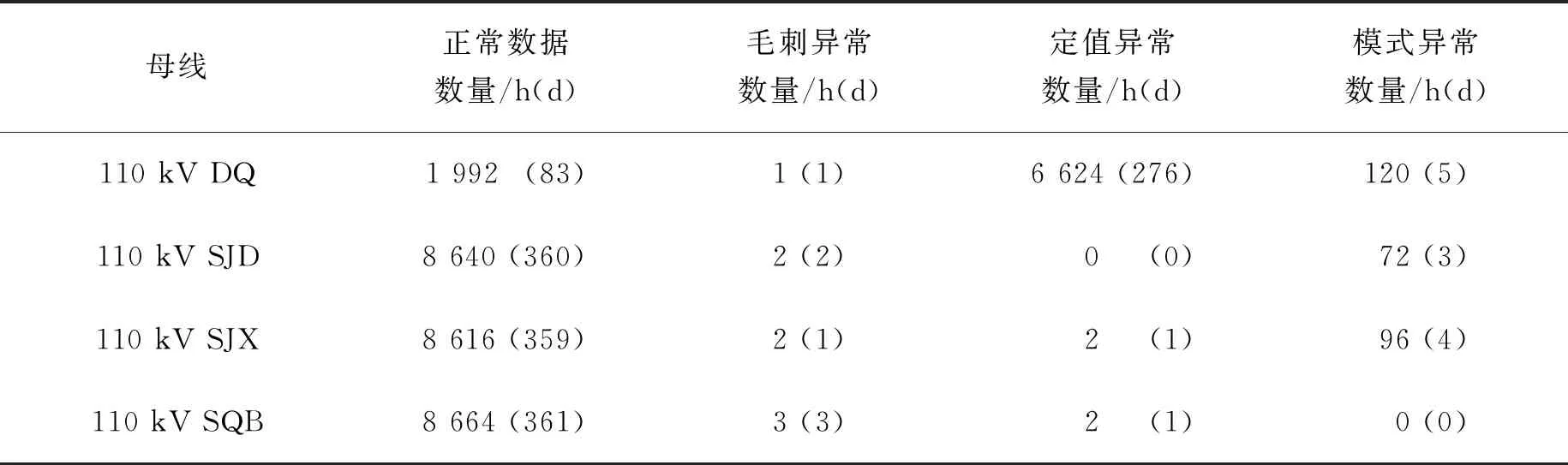
4.1 所提方法的合理性論證

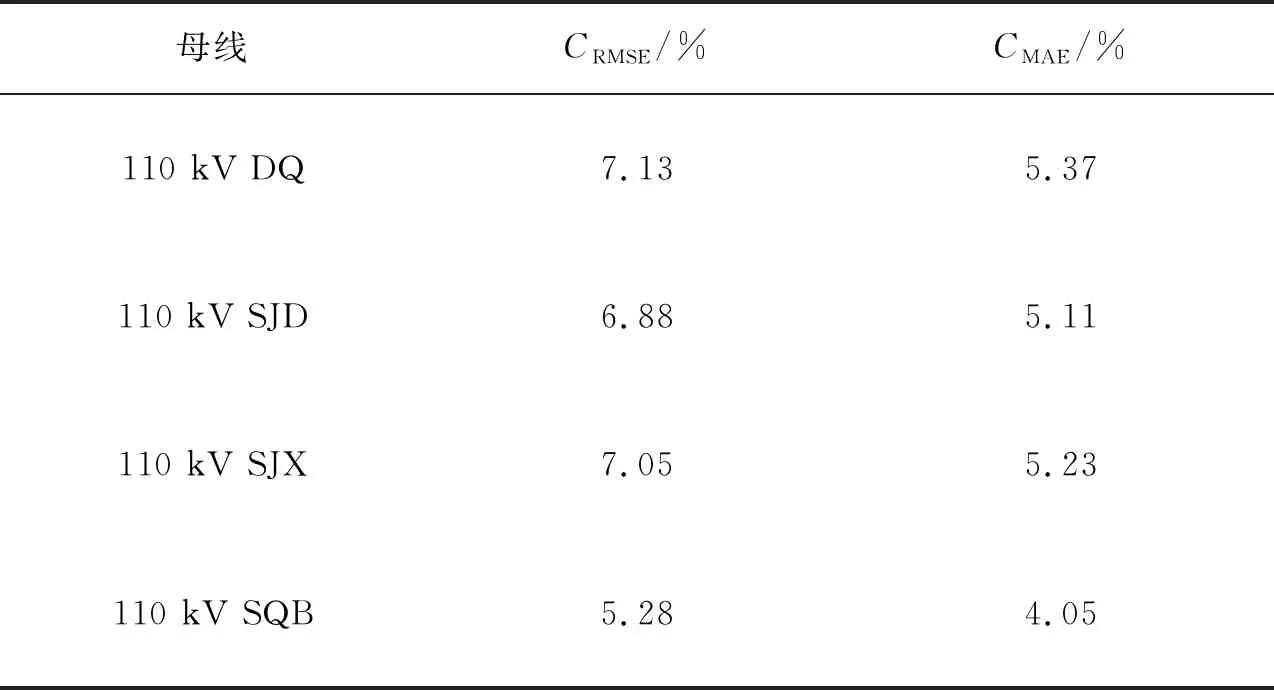


4.2 所提方法的有效性論證
4.3 所提方法的普適性分析
5 結(jié) 論

