基于混合優化算法的關節臂式測量機參數標定

章家巖, 許治順, 王 勝, 馮旭剛

(安徽工業大學 電氣與信息工程學院，安徽 馬鞍山 243032)

關節臂式坐標測量機是一種非笛卡兒式的柔性測量系統，通常在大型加工現場對不便移動的復雜零部件進行幾何尺寸的快速測量[1]，因其可操作性、靈活性和便捷性在工業生產與科學研究中得到廣泛的應用。由于其串聯式連桿機構，測量機的測量誤差會被累積并放大，同時機械加工精度、裝配誤差、磨損及環境因素等都對各連桿的幾何參數造成影響，與傳統的正交式坐標測量機相比，整體測量精度還存在較大差距。因此，測量機的誤差模型的分析及參數標定方法對于減少測量誤差有著重大意義。

目前已有眾多國內外學者針對關節臂式坐標測量機參數標定方法做了多方面研究。一類通過借助更高精度的測量儀器，如激光跟蹤儀、三坐標測量機[2]，或布置復雜的裝夾裝置[3]。例如：Acero等[4]研究了激光跟蹤儀作為參考儀器在AACMM參數標定中的可行性，但這類方法普遍成本高昂，系統復雜，時間效率較低且容易產生二次誤差[5]。另一類通過算法進行參數標定，一般為最小二乘法和智能尋優算法，例如：Santolaria等[6]使用一維球列作為標準件，采用Levenberg-Marquarat法(最小二乘法)對Faro的關節式坐標測量機進行了標定；Seyedhosseini等[7]應用改進的模擬退火算法對測量臂運動學參數的標定值進行了辨識。但采用標定算法對參數進行辨識時，常用的標定算法如最小二乘法在求解過程中存在初始值是非可行點時無法收斂、參數較多的復雜計算易產生積累誤差等問題，而尋優算法的局部搜索能力較差、容易陷入局部最小值。

針對關節式坐標測量機的參數標定問題，筆者提出了一種混合優化算法對測量機結構參數進行辨識。首先對最小二乘法求解中的Jacobian矩陣進行變換消除其中冗余參數，通過設定判定準則并實現模擬退火算法和最小二乘法的混合，結合兩者全局優化性能和高效局部的優化能力進行參數標定，提高測量機的測量精度。

1 關節臂式坐標測量機模型

關節臂式坐標測量機是仿人手臂的六自由度非正交坐標測量機，由機座、關節臂和測頭通過旋轉關節串聯連接構成[8]，結構參數名義值如表1所示，其結構如圖1所示。

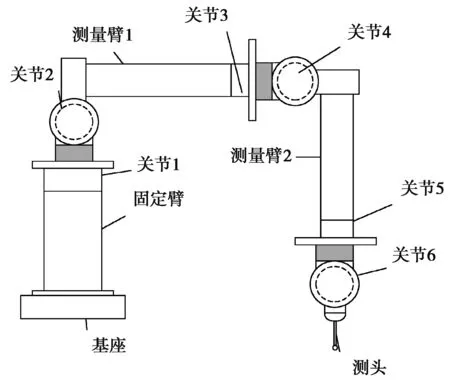
圖1 關節臂式坐標測量機結構示意圖Fig. 1 Configuration of articulated arm coordinate measuring machine

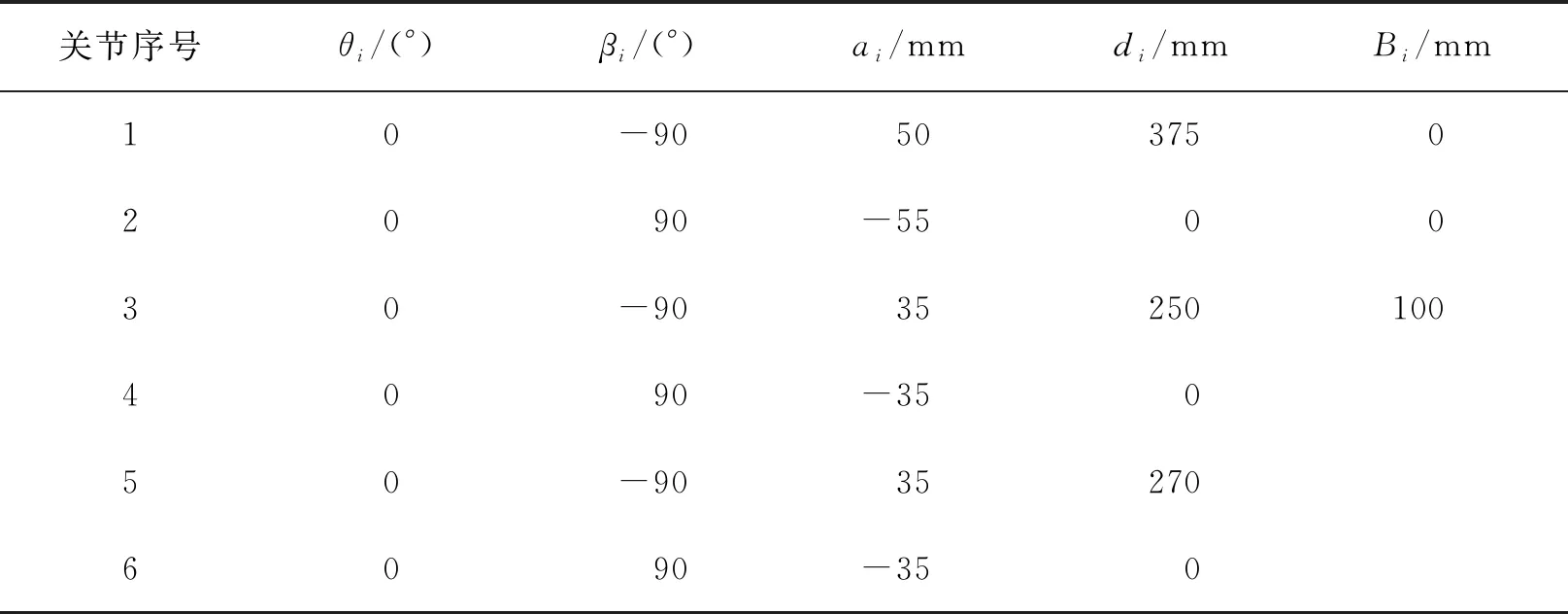
表1 結構參數的標稱值

1.1 D-H模型

1956年，Denavit和Hartenberg提出D-H方法描述相鄰連桿的變換關系，使用4個參數進行描述，分別是關節旋轉角θi，桿件的長度ai，桿件偏移量di，桿件扭轉角度βi。基于D-H模型的關節坐標轉換示意圖如圖2所示。

圖2 基于D-H模型的關節坐標轉換示意圖Fig. 2 Coordinate transformation diagram by D-H model

根據圖2可知，坐標系(xi-1,yi-1,zi-1)轉至下個坐標系(xi,yi,zi)的坐標的變換過程，需要經過2次旋轉2次平移得到，坐標轉換關系為

Ai-1,i= Rot(zn,θn+1)Trans(0 , 0,dn+1) Trans(an+1, 0, 0)Rot(xn+1,βn+1)。

(1)

相鄰坐標系的齊次變換矩Ai-1,i為

(2)

此時，由于第7個坐標系是以測頭為中心，由第6個坐標系平移，設測頭中心在坐標系下坐標為(Bx,By,Bz)，坐標轉換矩陣B為

(3)

基于D-H方法的關節臂式坐標測量機的坐標系統如圖3所示，根據公式(3)，六自由度關節臂式坐標測量機末端測頭相對于基座坐標系的數學模型可表達為

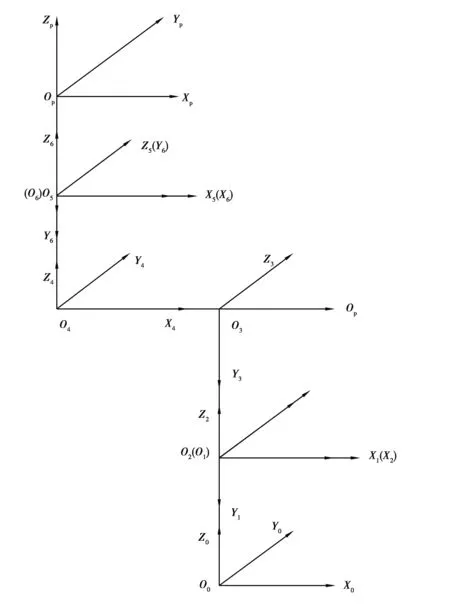
圖3 基于D-H模型的關節臂式坐標測量機的坐標系統簡圖Fig. 3 Coordinate system diagram of AACMM based on the D-H model

(4)

1.2 參數誤差模型

從公式(4)可以看出，測量機末端測頭的坐標值通過參數進行描述，則末端測頭中心坐標誤差與參數誤差{Δai，Δdi，Δβi，Δθi，ΔBi}有關。從式中可知共有27個參數誤差，Δai，Δdi，Δβi分別是關節的長度誤差、關節偏移量誤差和關節扭轉角度誤差，Δθi表示初始零點處的關節變量θi的零位誤差，ΔBi是測頭的裝配誤差。根據理論測量模型的參數誤差種類建立總誤差模型為

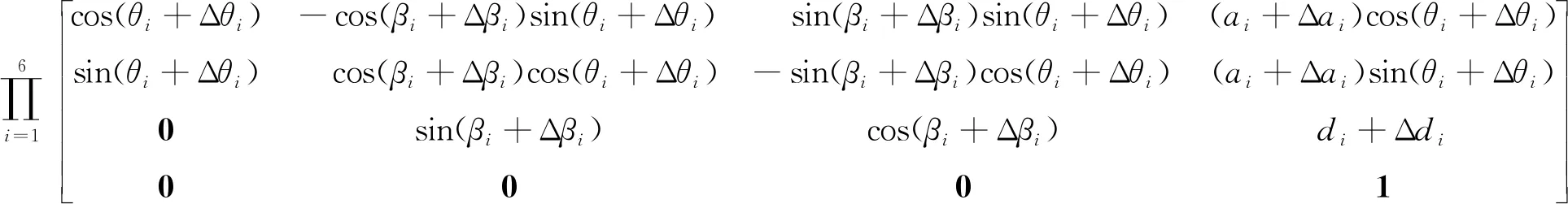
(5)

(6)

將公式(5)中的測頭坐標改寫為函數形式，對3組函數進行全微分數學解析，并將左右兩側分別展開寫成矩陣的形式，可得

(7)

式(7)等號右側3×27的Jacobian矩陣可用J表示，假設全部結構參數誤差足夠小，公式(6)可近似為

(8)

對式(8)進行簡化：ΔM=J·ΔS，ΔS為27×1的誤差參數矢量，ΔM表示為測頭坐標誤差模型。

2 目標函數和標定算法

關節式坐標測量機在測量同一點時，根據理論模型在不同的姿態時坐標值應該保持不變[9]，但結構參數與理論參數因多種因素存在誤差，此外，測量誤差還與空間位置有關[10]，所以標定時測量機應該在不同的位置進行多姿態的測量，坐標值的誤差大小和波動范圍都是測量機精度的體現。因此筆者結合兩者作為目標函數，采用設計的混合算法求取結構參數的實際值。

2.1 目標函數

根據上述內容，對錐窩進行不同姿態的測量，記錄所得的角度數據得到坐標值，設該點的真實值為多次測量數據的平均值，即

(9)

該點的誤差平均值是

(10)

該點的標準差為

(11)

關節臂式測量機的整體測量精度通過e和σ的組合來表示，目標函數為

OA=e+3σ。

(12)

通過目標函數的值來判定測量機計算所得的結構參數是否接近真實值。

2.2 去除冗余參數的最小二乘法

根據公式(8)，運用最小二乘法計算可得

ΔS= (JT×J)-1×JT×ΔM。

(13)

根據式(13)計算出ΔS后對系統參數進行修正，通過修正后的參數計算出新一輪的理論坐標值及誤差矩陣，判定修正后參數的誤差小于設定的閾值ε，不滿足條件就繼續迭代；滿足條件則運算結束，輸出最終的參數。

當上述公式中雅克比矩陣J為奇異陣時，如果矩陣中有部分參數為線性關系，會對參數誤差的求解造成干擾。因此對誤差模型ΔS的等式左側進行變換分析：

ΔS= (JT×J)-1×JT×ΔM?ΔM?(JT×J)×ΔS=JT×ΔM。

(14)

令式(14)中K= (JT×J)-1，并對其進行奇異值分解：

(15)

式中:P,Q為正交陣;Λ表示對角陣(Λ=diag(φ1,φ2,...,φr)),則對角陣的秩r即為Jacobian矩陣的秩。將矩陣K代回式(15)可得

(16)

根據對式(16)中的矩陣分析，得知結構參數中有25-r個參數有線性關系。由于式(15)中K是對稱矩陣，那么有對應的關系式QT=P-1，因此Q陣屬于旋轉矩陣，對式(16)的誤差ΔS模型進行旋轉變換，將所有呈線性相關的結構參數處在相同的零平面上[12]。隨后將QT中后25-r行的部分做初等行變換從而提取矩陣中有線性關系的誤差參數，最終所得結果為

Δa6=Bz·Δθ6，Δd6=-Bz·Δβ6。

(17)

由于Bz已知，因此公式(17)中參數a6，θ6，d6，β6無法同時進行標定，選擇2個參數作為冗余參數并在Jacobian矩陣及參數誤差矩陣ΔS中去除對應參數的矩陣，可得新的結構參數誤差公式，其中矩陣ΔS為r行1列，矩陣J為3n行r列，矩陣ΔS為3n行1列，即

(18)

2.3 混合退火最小二乘算法設計

模擬退火是模擬統計物理學中的固體退火過程[12-13]，適用于求解不同的非線性復雜問題，算法有解空間、能量函數和初始解3部分，它的解題思路是在對初始解隨機擾動產生新解，代入能量函數判斷是否滿足Metropolis準則，根據冷卻系數讓溫度下降使能量函數達到平衡狀態； Metropolis抽樣準則具有概率性地跳出局部最優“陷阱”的優點[14]。

為計算出優化權值，將上文的目標函數設為能量函數E=f=e+3σ。

算法步驟如下：

Step 1 設定初始值。給定初始溫度T0始權參數w(0)=w0，設置終止檢驗精度e，終止溫度Tmin，馬爾可夫鏈的鏈長L，令初始最優解w*=w0，迭代次數i=0。

Step 2 產生新解。令ωβ=ω(k)+R×E產生新解，其中R為區間[-1, 1]的隨機數,符合Cauchy分布。

Step 3 求優化函數指標。計算ΔE=E(wβ)-E[w(k)]。

Step 4 接受判斷。如果ΔE≥0，計算接受概率r=exp[-E(εβ)/T]，如果r>p，則w(k+1)=wβ，否則w(k+1)=w(k)，p為區間[0, 1]上的隨機數；如果ΔE<0，則w(k+1)=wβ，w*=wβ。

Step 5 穩定性判別。k=k+1，如果k>L，則轉到step 5，否則轉到步驟2。

Step 6 降溫T=Ti+1=αTi，i=i+1。

Step 8 輸出最終最優解w*，中止算法。

融合算法的關鍵在于如何選擇兩者算法的轉折點[15]，最通用的方法是選擇固定的溫度次數，雖然簡便但針對不同模型具有通用性，往往須通過大量的實際經驗才能得到大致范圍。因此，采取判定適應度的方式融合兩種算法，如果同一溫度的多個不同最優值之間的差值小于某一設定值，那么結束模擬退火算法轉入最小二乘法。

適應度公式為

轉換準則為

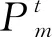
由上可知，融合算法的過程如下：先采用SA算法計算，若滿足切換準則表明進入全局最優解的區域，退出SA算法，將滿足準則的解作為LM算法的初值代入，通過運算得到最優解，具體的流程圖如圖4所示。

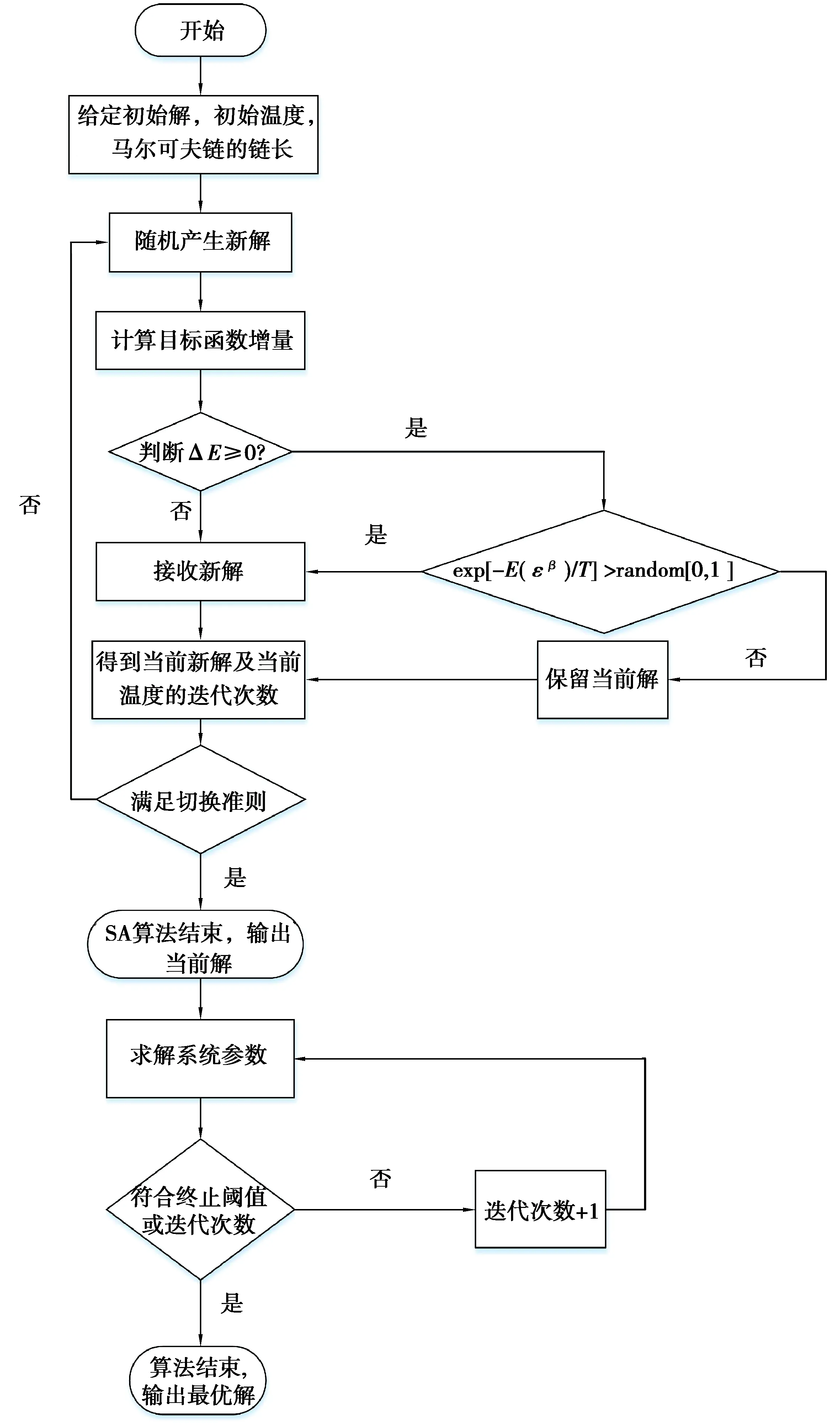
圖4 混合算法的流程圖Fig. 4 Flow chart of the hybrid algorithm

3 實驗分析

為了減少隨機誤差的影響，對錐窩中心點進行測量，關節臂式坐標測量機從不同方向上測量同一點(即改變各關節旋轉角度)獲得空間三維坐標數據，測量結束后改變錐窩的空間位置重復上述步驟，測量示意圖如圖5所示。運用最小二乘法通過分析線性相關的結構參數，將其中2個不參與標定的參數設為理論值，而裝配測頭參數誤差(ΔBx,ΔBy,ΔBz)中前兩項為0，設Bz的值為100 mm，故整個關節臂式坐標測量機的結構參數誤差共有23個。為了減少溫度誤差的影響，室溫保持20 ℃，根據表1的名義參數和測得的角度數據得到坐標值，用混合算法進行誤差參數標定，計算所得的結構參數誤差如表2所示。

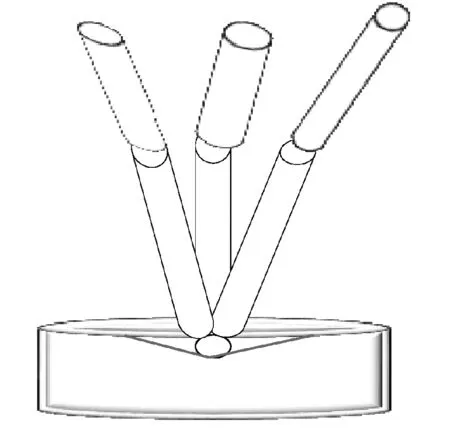
圖5 測量示意圖Fig. 5 Schematic diagram of the measurement

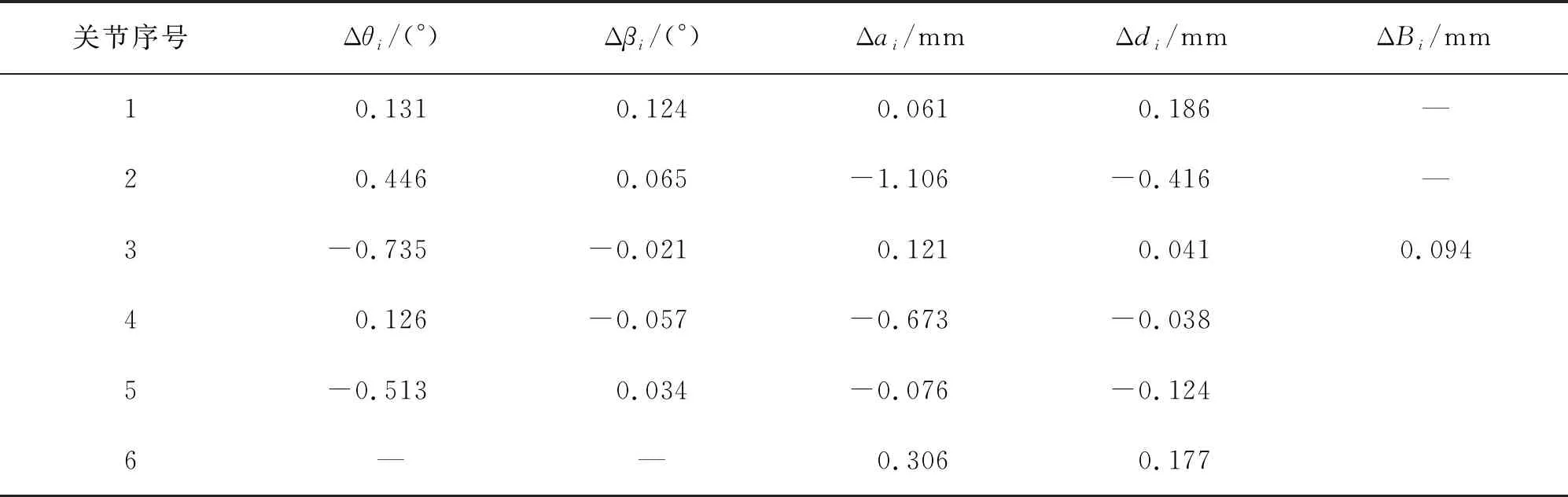
表2 基于混合算法標定的各項結構參數誤差

為了驗證所提算法得到的誤差參數的準確性，將計算得出的參數誤差代入結構參數名義值，得到修正后的測量機結構參數。分別采用辨識前后的參數，對兩者的誤差進行對比。關節臂式坐標測量機對錐窩進行測量獲得角度數據，每測10次數據后錐窩換一次位置，設該點坐標真值為多次測量值的平均值，計算單點重復性誤差；此外，長度誤差也是測量機整體精度的重要部分，為了驗證標定算法的有效性，關節臂式測量機先對錐窩進行多次測量，然后改變錐窩的位置再測多次，獲得數據后計算空間每組兩點之間的長度測量誤差，公式為

(19)

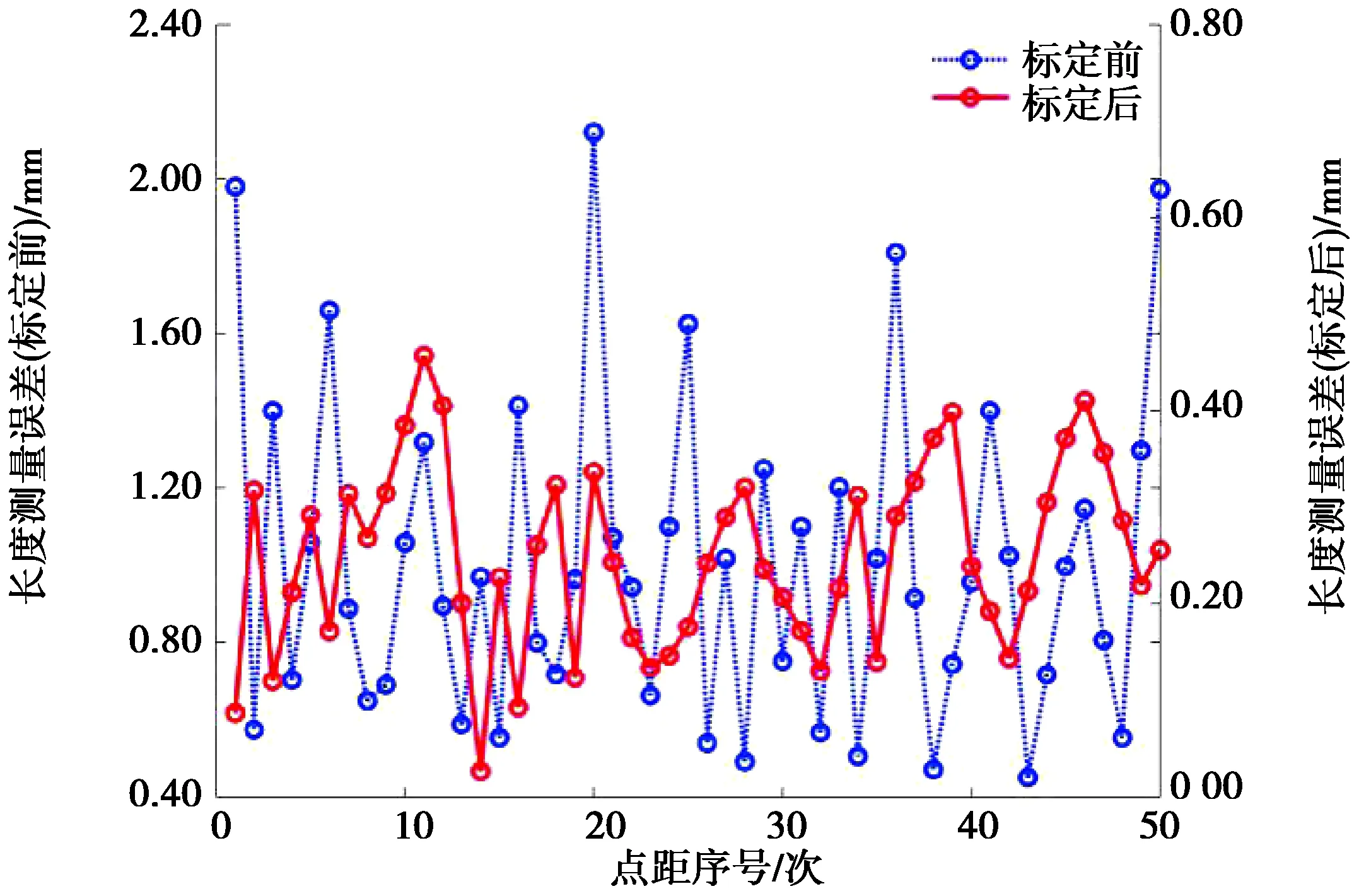
圖7 參數辨識前后長度誤差Fig 7 Length error based on different structural parameters

由圖6～7分析可知，參數辨識前，測量機的單點重復性誤差范圍在1.571 ～2.136 mm，平均值為1.873 mm，標準差為0.106 mm；參數辨識后，測量機的單點重復性誤差在0.097 ～ 0.166 mm，平均值為0.127 mm，標準差為0.019 mm。參數辨識前長度誤差范圍在0.486 ～ 2.116 mm，平均值為1.038 mm，標準差為0.426 mm，參數辨識后長度誤差范圍在0.025 ～ 0.448 mm，平均值為0.092 mm，標準差為0.097 mm。實驗結果表明，混合優化算法有效地提高了測量機的測量精度。

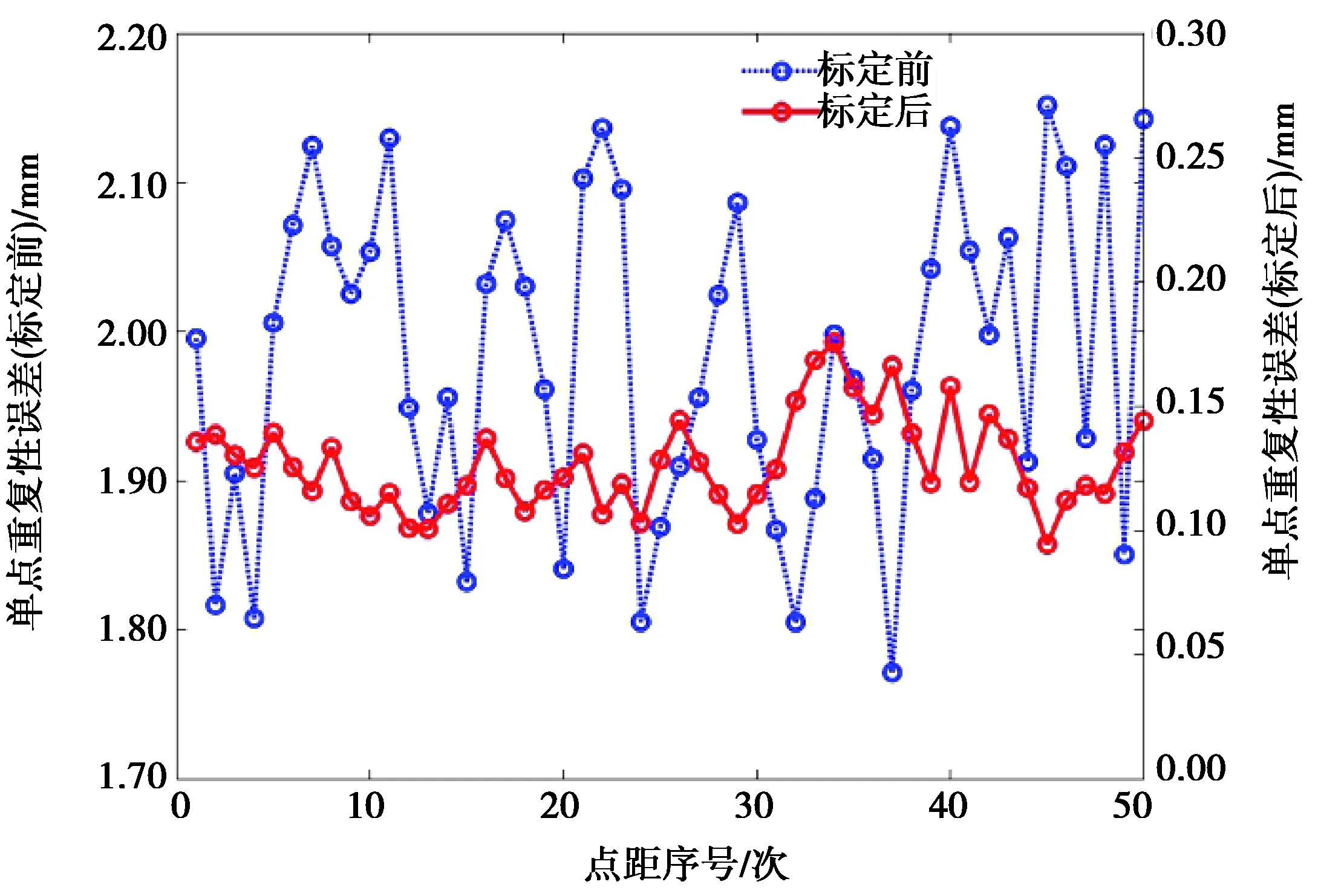
圖6 參數辨識前后單點重復性誤差Fig. 6 Single point repeatability error based on different structural parameters

4 結 論

在關節臂式坐標測量機測量模型分析的基礎上對標定算法進行了研究，結論如下：

1)采用最小二乘法標定結構參數過程中，針對呈線性相關的誤差參數無法準確地求出參數誤差解的問題，對Jacobian矩陣變換分析，去除了方程中的冗余參數，提高了標定精度也減少了計算量。

2)基于模擬退火算法與最小二乘法的優缺點，通過設定判定準則來混合兩種算法，既充分利用了SA的全局優化性能和最小二乘法算法的高效局部優化特點，又解決了最小二乘法初值設定問題。

3)通過實驗結果分析，運用混合優化算法補償了關節臂式坐標測量機結構參數誤差后，測量機的準確性和重復性都得到了顯著的提升，測量誤差得到了進一步的抑制。