接觸器觸頭彈跳行為規律分析及算法優化

黃克鵬，王發展，趙明基，李亞峰，區達銓

(1. 西安建筑科技大學 機電工程學院，西安 710055；2. ABB新會低壓開關有限公司，廣東 江門 529000)

交流接觸器是一種廣泛使用的低壓電氣開關，隨著電氣產品的發展，對接觸器的性能指標要求也越高。接觸器通電時，動靜觸頭產生的碰撞彈跳現象引起電弧對觸頭的燒蝕作用會降低接觸器的電壽命[1-2]。故準確分析并掌握其動態特性變化規律，有效減少和抑制觸頭彈跳，對于交流接觸器的優化設計具有重要的意義[3-4]。

目前，國內外學者對交流接觸器進行了大量的研究和優化工作。在文獻[5-8]中，作者通過可控電磁反力，對交流接觸器進行了仿真分析，得到了部分有益結果。文獻[9-12]基于ANSYS有限元法，對合閘過程中的電磁力進行了仿真分析，但并未考慮摩擦和碰撞阻尼的影響。文獻[13-14]的作者建立接觸器數學模型，并進行合閘過程的動態分析，但有關觸頭碰撞前后的彈跳研究較少。文獻[15]運用遺傳算法對接觸器進行了優化設計，但該文采用了均勻磁場來模擬電磁吸力，對模型做了大量簡化，使得誤差偏大。文獻[16-18]利用ADAMS軟件建立交流接觸器的三維動態仿真模型，分析了觸頭彈跳的相關影響因素，由于對電磁力進行了大量線性化處理，使得仿真結果不能準確反映觸頭彈跳過程。

綜上所述，國內外少有結合機械結構本身考慮的觸頭彈跳問題，由于觸頭彈跳也是觸頭系統的振動過程，筆者通過接觸器觸頭彈跳行為規律，將ADAMS軟件與遺傳算法相結合，對觸頭系統的參數進行優化設計。

1 接觸器觸頭模型建立與規律分析

交流接觸器由觸頭系統、電磁系統和觸頭支架3部分組成(見圖1)。接觸器工作時，先給電磁線圈通電，當電磁力大于反力彈簧作用力時，動鐵芯通過觸頭支架使動觸頭向下運動，由于動靜觸頭間距小于動靜鐵芯間距，使得動觸頭先于動鐵芯發生撞擊和彈跳。此時動鐵芯繼續向下運動，直至動靜鐵芯發生碰撞[19]。

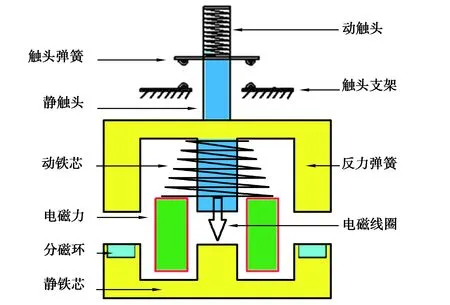
圖1 交流接觸器結構圖Fig. 1 Schematic diagram of the AC contactor

觸頭彈跳引起的機械振動現象存在于交流接觸器整個工作過程中，由于動、靜觸頭以及動、靜鐵芯間的碰撞接觸均具有間斷特征，使交流接觸器的動力學特性出現不連續性現象。其運動模型如圖2所示。

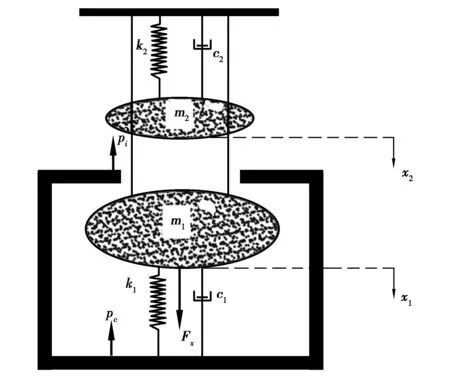
圖2 交流接觸器運動模型Fig. 2 Motion model of AC contactor

設m1、m2分別為動鐵芯和動觸頭質量；x1、x2分別為動鐵芯和動觸頭位移；c1、c2分別為電磁機構和觸頭系統等效阻尼；k1、k2分別為反力彈簧和觸頭彈簧剛度系數；Fx為電磁力；pi、pc分別為觸頭以及鐵芯碰撞時的接觸力。

接觸器合閘運動過程中，考慮動靜觸頭碰撞接觸力pi，動靜鐵芯碰撞接觸力pc。其運動微分方程分別為

(1)

電磁力作為整個電磁機構動力來源，計算的準確程度會對整個裝置的運動過程產生很大影響，為了確保電磁力計算的準確性，本文中采用的電磁鐵動態吸力公式為

(2)

式中：μ0為真空磁導率，S為磁路截面積，k為漏磁系數，δ為氣息長度，N為線圈匝數，i為電流。

為進一步分析接觸器二自由度分段耦合系統中影響因素，假定系統的激勵為簡諧形式，即Fx=F0sinωt(其中，F0為幅值，ω為頻率)。由于碰撞接觸力較小，在求解過程中可忽略不計，故將接觸器的實際運行過程可以等效為如圖3所示的兩階段。

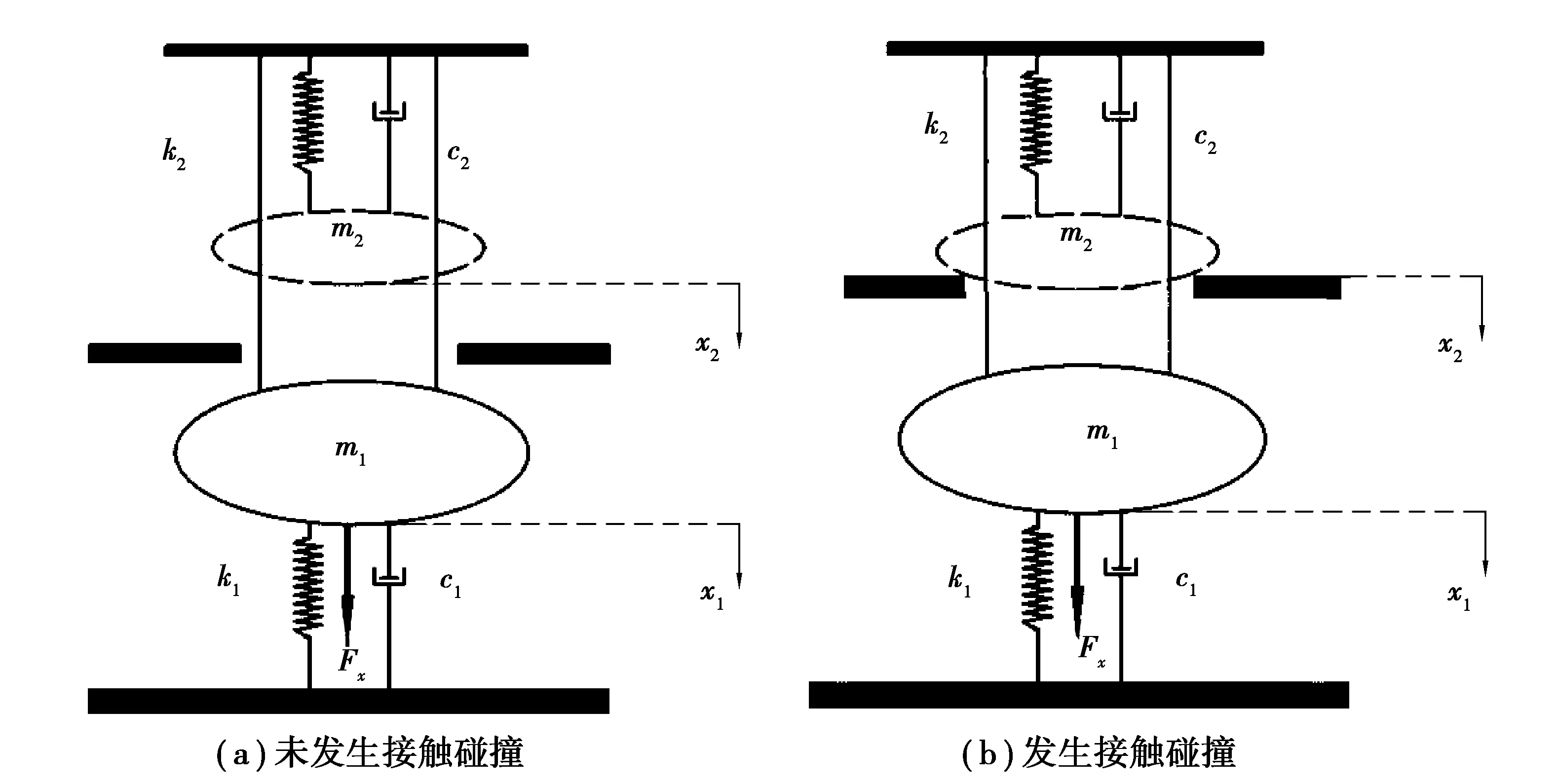
圖3 分段簡化模型Fig. 3 Piecewise simplified model

階段1，當動靜觸頭和動靜鐵芯均未發生接觸時，動觸頭與動鐵芯由于通過觸頭支架相連，所以共同向下運動。如圖3(a)所示，其方程可表示為

(3)

假設其解的形式為xj(t)=Xjeiωt,j=1,2；帶入式(3)后可求得穩態解的振幅為

(4)

(5)

階段2，當動靜觸頭接觸，動靜鐵芯未接觸時，此時動觸頭和動鐵芯分離，只有動鐵芯向下運動，如圖3(b)所示，假設系統的運動是簡諧的，即x1(t)=F0sinωt；通過定義相對位移x：x=x2-x1；其方程可表示為

(6)

由此可以得出穩態解的振幅為

(7)

以ABB公司A9-30-10型電磁接觸器為例，將各項參數帶入到上述方程中求解，表1給出了各項參數值。

表1 接觸器結構參數表

求解結果如圖4所示。從圖4可知，動觸頭從開始移動到發生初次碰撞的時間為0.019 0 s，其碰撞瞬間速度為1.293 m/s，在0.021 9 s時達到穩定合閘狀態；動鐵芯在0.019 7 s發生初次碰撞，其碰撞瞬間速度為1.687 mm/s，在0.021 1 s時達到穩定接觸。對比可知：動觸頭開始彈跳時間早于動鐵芯，這是由于動靜觸頭距離小于動靜鐵芯距離，導致動觸頭先于動鐵芯發生撞擊和彈跳。

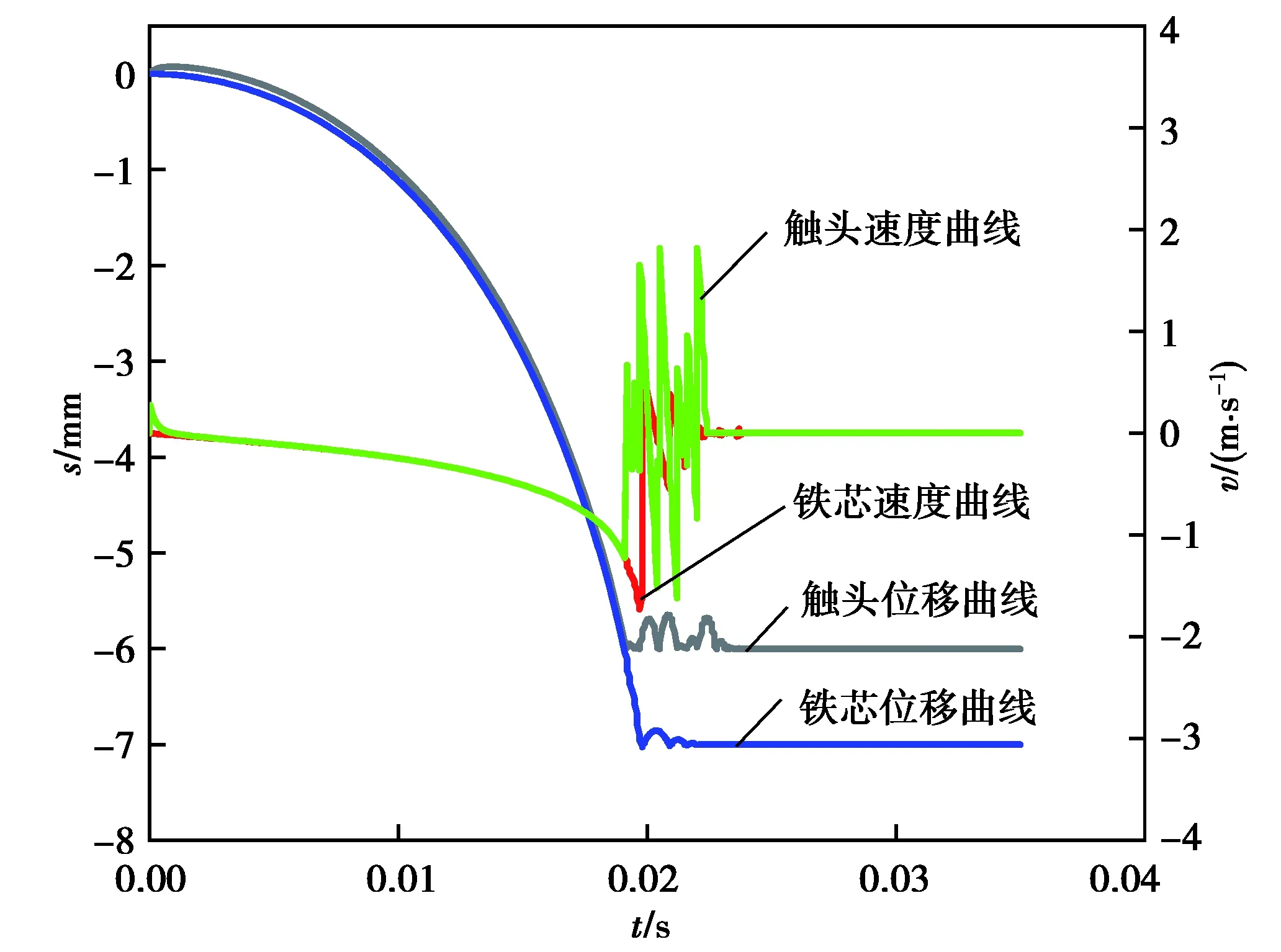
圖4 觸頭和鐵芯彈跳響應曲線Fig. 4 Bounce response curve of contact and core

由動鐵芯位移曲線可知，動鐵芯的彈跳次數和最大位移均小于動觸頭，這是由于動鐵芯撞擊時接觸面積較大，在彈跳過程中受到電磁力作用，且動鐵芯質量較大，進一步阻止了動鐵芯的彈跳，使得其彈跳次數和時間遠小于動觸頭。分析可知，觸頭初次碰撞時的最大位移較小，其碰撞時的最大位移出現于動鐵芯初次撞擊時刻，這是由于動靜鐵芯的碰撞進一步加劇了觸頭彈跳，使得其彈跳最大位移增加。

2 仿真模型的建立

2.1 電磁力ANSYS仿真

在實際電磁力計算中，由于線圈中的交變電流產生磁場，動鐵芯的運動又會在線圈中產生感應電流，使得線圈中磁場分布變得非常復雜，以往研究者多采用簡化算法，通過公式直接計算電磁力，使得計算量較大且精度偏低。

利用多物理場分析軟件ANSYS，對動靜鐵芯間的電磁力進行仿真計算。有限元仿真分析遵循靜態電磁場原理，不存在時變效應。通過對物體表面的麥克斯韋電磁應力張量進行表面積分，可獲得靜態場條件下作用在物體上的電磁力。ANSYS有限元分析軟件建立了交流接觸器有限元模型，然后利用SOURC36單元創建了3D跑道型線圈，線圈匝數設置為1 600閘，施加了磁力線邊界條件，仿真得到的電磁力曲線如圖5所示。

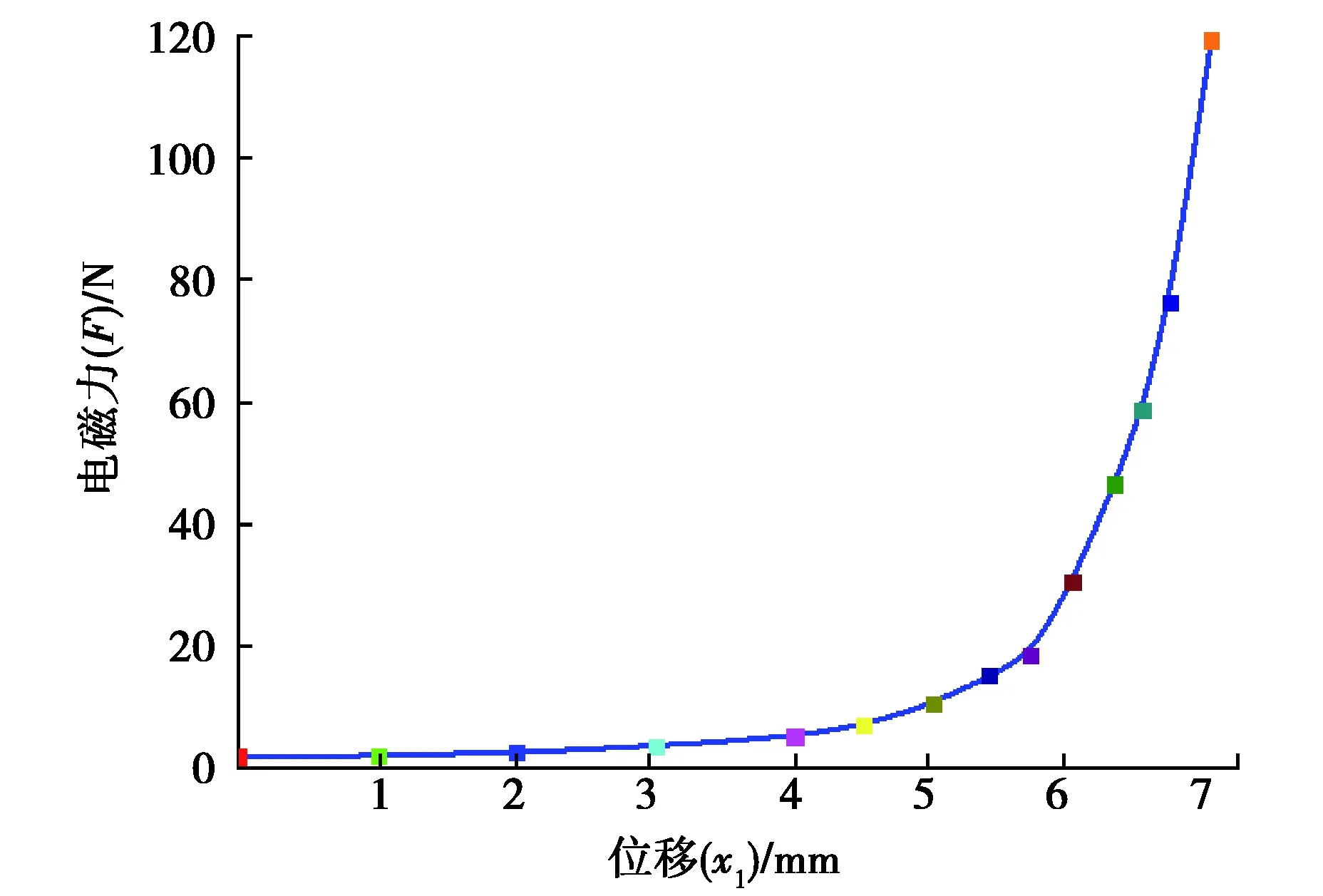
圖5 電磁力仿真Fig. 5 Electromagnetic force simulation

由圖5可知交流接觸器的電磁吸力隨著動鐵芯位移的增大而增大。當電磁系統中其他參數一定時，由式(2)可知，線圈匝數N的增大使得電磁吸力Fx增大，過大的電磁吸力使得鐵芯碰撞速度快，導致碰撞加劇。當線圈匝數較小時，電磁力又不能保證接觸器快速合閘、穩定吸合，電磁吸力大小與線圈匝數N的圈數成正比關系。

2.2 接觸器ADAMS模型建立

根據ABB公司A9-30-10型電磁接觸器為參考，采用ADAMS動力學分析軟件對交流接觸器合閘全過程進行動態仿真。運用二元函數插值法，將上述ANSYS仿真得到離散的磁鏈和電磁吸力數據用樣條函數的方法輸入到ADAMS中。通過插值法迭代的方式對函數值進行求解，并將求解結果作為交流接觸器機械模型的驅動力，從而實現對交流接觸器動態合閘過程的仿真。

為了提高計算精度，仿真過程中還考慮了碰撞阻尼和摩擦力等因素的影響。對靜鐵芯和靜觸頭施加固定副，動鐵芯和動觸頭施加移動副，對動靜觸頭以及動靜鐵芯接觸面均施加接觸副，設置模型中各個部件的結合參數與材料屬性，仿真時長為0.035 s，以步長500步進行動態合閘仿真。ADMAS中的仿真模型如圖6所示。

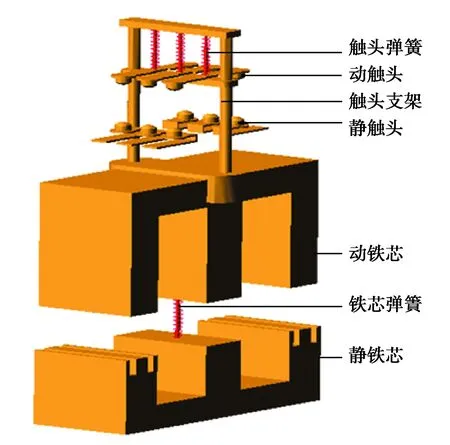
圖6 接觸器仿真模型Fig. 6 Contactor simulation model

3 改進型遺傳算法

3.1 遺傳算法

遺傳算法(genetic algorithm，GA)是一種仿照生物遺傳和進化的算法，其本質是根據適應度函數值來評價問題解的優劣，從而實現對解空間的搜索。GA具有強魯棒性和高效的全局搜索能力，目前已被成功運用于解決多峰值、非線性、高復雜度等工程實際。GA可以用一個五維向量組來描述，即

XGA=[Npop,Ngen,P,feval,fset]，

(8)

式中：Npop為種群規模，Ngen為迭代次數，p為遺傳算子(交叉pk和變異pz)，feval為適應度函數，fsel表示再生選擇規則。

由于GA早熟收斂和算法參數敏感，使得算法進化后期搜索效率較低，并且GA需要人為設定3個遺傳參數，即所選群體的大小n、交叉概率pk與變異概率pz)。Sriniva等因此首次提出AGA算法，該算法可使得交叉變異概率實現適應度值動態調整，從而獲取適合當前個體的最佳交叉變異概率，使搜索能力和效率大幅提高。

3.2 改進的自適應遺傳算法

3.2.1 群體生成與子代產生機制

采用解空間的均勻采樣法，先在解空間中隨機均勻生成一定數目的個體，按照適應度值的大小進行排序，挑選出優秀個體組成初始群體。

遺傳算法主要通過選擇、交叉和變異等操作來產生子代個體，但經過這些操作產生的子代并不一定優于父代中的個體，會造成父代中優良個體的丟失。因此，對子代產生機制進行改進，將子代群體的產生分成3部分：首先采用精英保持策略，將父代群體中前10%的優良個體直接保持到子代，使得父代中的最優解可不被交叉和變異破壞；其次采用隨機生成方式，產生10%的子代個體，補充種群中基因型的多樣性；第三部分采用選擇、交叉、變異產生剩余子代的80%；最后采用該方法可使群體中優良個體得以保存，同時增加和維持了群體的多樣性。

3.2.2 算子改進機制

AGA對傳統GA中的交叉變異概率進行了改進，使交叉變異概率不再是人為設定的固定值，而是可以隨著種群中個體的相似度進行動態調整。當種群中父代個體相似度較高時，執行交叉操作就很難產生新的個體，可以有效避免局部最優的情況，抑制早熟收斂現象的發生；當種群中個體的相似度較低時，說明此時種群多樣性較高，可以防止種群中的優良基因結構遭到破壞。

AGA算法中交叉變異概率的值是個體適應度和最大適應度的差值成正比關系，最大適應度與平均適應度的差值成反比關系，當群體中某個體適應度值與該代中個體最大適應度值相等時，將導致交叉變異概率為零，使優化問題早熟[20]。AGA算法使得交叉概率和變異概率可以根據個體適應度取到合理的值。具體計算公式為

(9)

(10)

式中：f為個體的適應度值，fmax為群體中最大適應度值，fmin為群體中最小適應度值，favg為群體平均適應度值，其中pk1>pk2>pk3∈(0,1)，pz1>pz2>pz3∈(0,1)。

3.3 設計變量及約束條件

影響觸頭彈跳的主要因素包括動觸頭m1、動鐵芯m2、動鐵芯位移x1、動觸頭位移x2、觸頭彈簧剛度系數k1、反力彈簧剛度系數k2、觸頭系統等效阻尼c1、電磁機構等效阻尼c2、電磁力Fx(可用線圈匝數N代替)。

因此選取對觸頭彈跳影響的9個參數作為此次接觸器的優化變量，具體公式為

X=[m1,m2,x1,x2,c1,c2,k1,k2,N]T，

(11)

為了保證算法能得到可靠合理的解，必須對交流接觸器模型各設計變量施加約束條件。具體數值及變化范圍如表2所示。

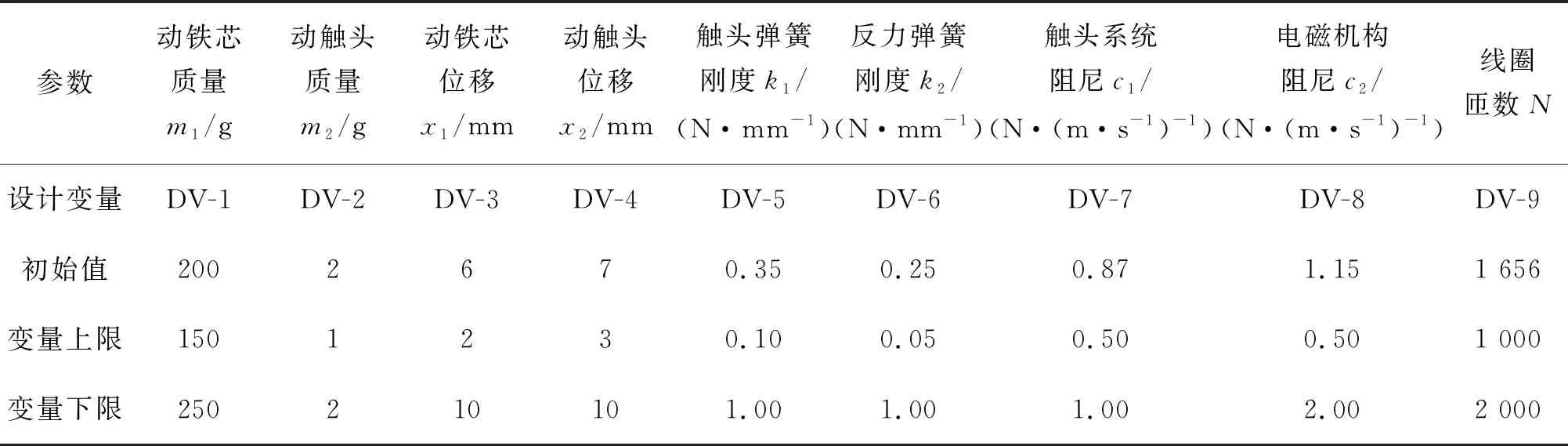
表2 設計變量原始值及其變化范圍

3.4 目標函數及適應度函數

在保證交流接觸器正常工作的前提下，以觸頭合閘和觸頭彈跳時間作為優化目標，則此次接觸器優化的目標函數為

minf(X)=[T(X),ΔT(X)]T，

(12)

式中：T(X)為觸頭合閘時間，ΔT(X)為觸頭彈跳時間。

當接觸器運行時，運行函數為f(X)，具體表達式為

f(X)=step(x,x0,h0,x1,h1)，

(13)

式中step為ADAMS自帶函數。

將以上各個單項優化目標函數按照線性加權的方法，統一成如下綜合目標的適應度函數

(14)

式中，w1+w2=1。其中w1、w2為目標函數的加權因子，T0、ΔT0為優化前的各目標函數的值。

3.5 算法優化流程

針對交流接觸器中的觸頭質量、鐵芯質量、觸頭彈簧以及電磁線圈匝數等參數優化，算法流程如圖7所示。

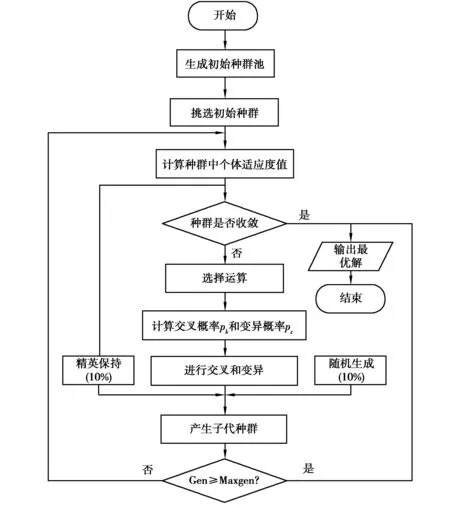
圖7 改進遺傳算法流程圖Fig. 7 AGA algorithm flow chart

STEP1：設定改進自適應遺傳算法的初始參數，包括編碼類型、初始種群大小、遺傳迭代數和交叉變異概率等初始參量。

STEP2：采用解空間均勻采樣法，均勻隨機生成初始種群池，挑選初始種群。

STEP3：對初始種群進行適應度計算，首先采用精英保持策略，將初始種群中前10%優秀個體直接保持到子代。其次判斷種群是否滿足收斂條件。若滿足，輸出結果，否則執行STEP4。

STEP4：進行遺傳操作，選擇80%的父代個體，根據群體中個體適應度值，計算個體的交叉變異概率，進行交叉和變異操作。

STEP5：將采用精英保持策略，隨機生成機制，運用選擇、交叉和變異操作產生的個體構成新的子代種群。

STEP6：判斷種群遺傳代數是否超過設定值，若是，輸出結果，否則遺傳代數加1，返回STEP3。

4 基于AGA算法的接觸器優化

4.1 遺傳算法程序在ADAMS中的動態鏈接

使用C語言編寫遺傳算法代碼，利用VC++6.0調試器編譯添加程序生成動態鏈接庫文件，實現對自編譯的算法的注冊。通過設置“USER1”接口，將遺傳算法添加到ADAMS中。經過算法優化后，將新獲得的參數供ADAMS/View調用。

4.2 優化結果及分析

在ADAMS/View的菜單欄中，選擇“Simulate”中的“Design Evaluation Tools”選項，然后選擇“Optimizer”，進入到“求解器設置”對話框中的“Algorithm”選擇用戶自定義的“USER1”接口，對樣機模型進行優化。

圖8為遺傳算法優化前觸頭彈跳曲線。從圖8可以看出優化前接觸器動觸頭從通電到初次合閘所需時間為19.71 ms，其彈跳過程中的最大位移為0.284 1 mm，碰撞瞬間速度為1.293 m/s，彈跳的總時間為2.9 ms，動觸頭彈跳4次后慢慢趨于穩定，由于動靜觸頭之間存在Hertz接觸，故彈跳曲線向后延伸了一小段。動鐵芯于20.8 ms時發生初次碰撞，其彈跳過程中的最大位移為0.124 1 mm，彈跳的總時間為1.7 ms，碰撞瞬間速度為1.687 mm/s，在0.021 9 s時達到穩定合閘狀態，動鐵芯彈跳2次后即達到了穩定狀態。

圖9為遺傳算法優化后觸頭彈跳曲線。從圖9中可以看到優化后動觸頭微小彈跳就達到了穩定合閘狀態，動鐵芯并未發生明顯彈跳，碰撞瞬間為1.187 mm/s；動觸頭合閘所需時間為23.32 ms，動觸頭碰撞瞬間速度為1.352 mm/s，其彈跳過程中的最大位移為0.021 2 mm，觸頭彈跳總時間為0.32 ms。對比圖8可知，通過遺傳算法優化后，接觸器動觸頭彈跳總時間降低了89%，最大位移降低了93%，碰撞瞬間速度為降低了8.9%；動鐵芯彈跳總時間降低了95%，最大位移降低了83%，碰撞速度降低了19.9%，接觸器整體性能得到了大幅提高。

圖8 遺傳算法優化前觸頭彈跳曲線Fig. 8 Contact bounce curve before optimization of genetic algorithm

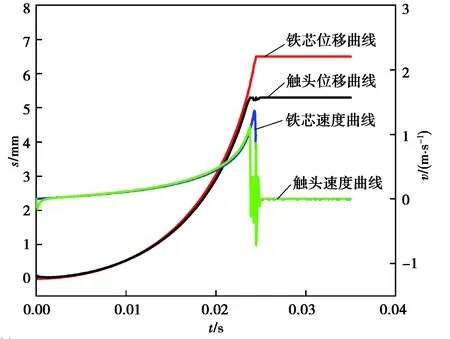
圖9 遺傳算法優化后觸頭彈跳曲線Fig. 9 Contact bounce curve after optimization of genetic algorithm

接觸器優化前后的各項參數如表3所示，由表3中優化前后對比可知，顯然優化后動鐵芯質量減小，動觸頭質量增加；動鐵芯和動觸頭位移均減小；電磁機構和觸頭系統等效阻尼均增大；反力彈簧和觸頭彈簧剛度系數均增大；線圈匝數減小，即電磁力減小，樣機動態特性得到了大幅提高。

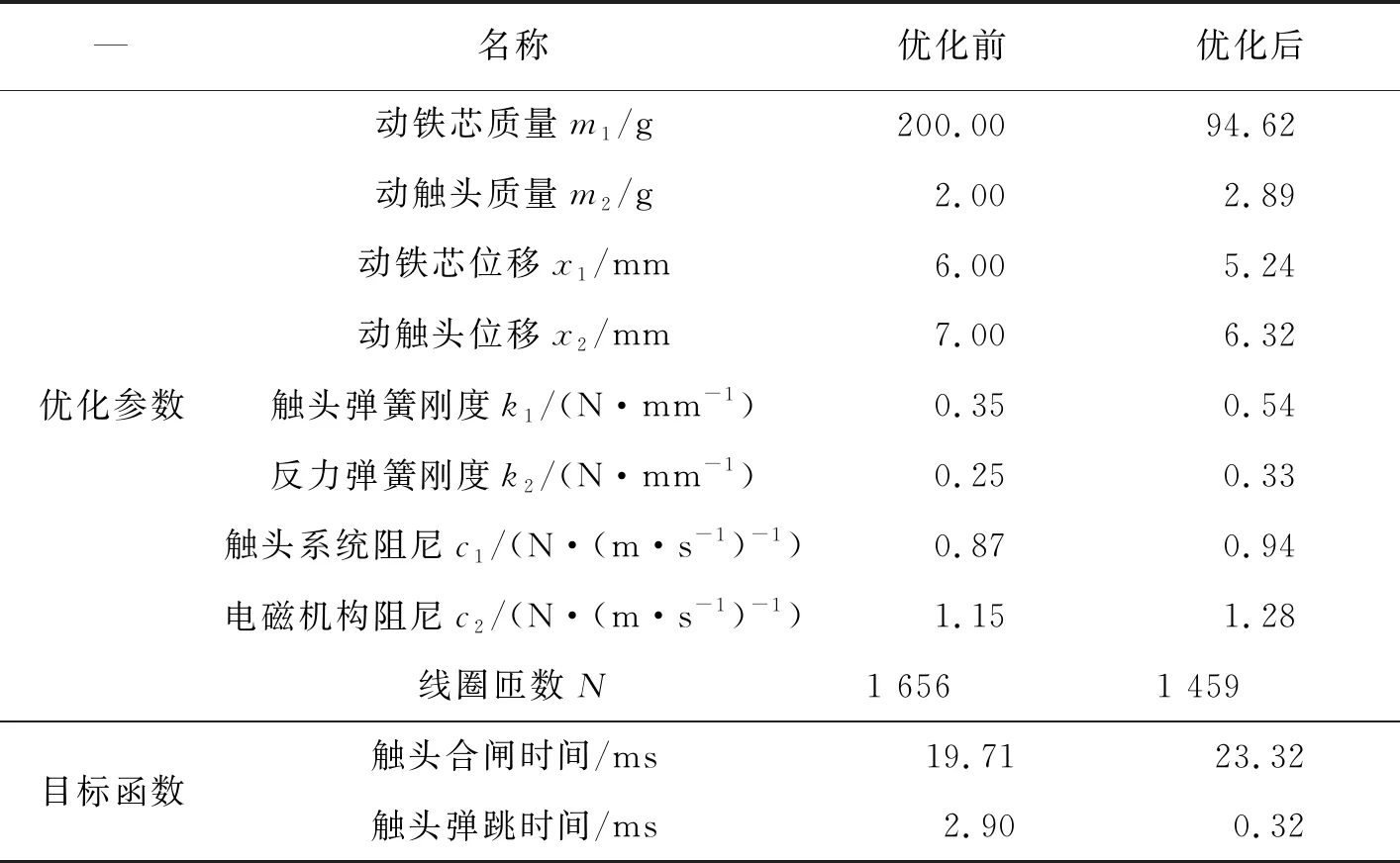
表3 參數優化結果對比表

5 實驗及對比

本實驗依托ABB江門公司實驗平臺，對優化后的模型進行驗證。首先，將優化后的模型參數按1 ∶1進行實際生產，其生產過程中，觸頭所用材料為AgNi15，觸橋所用材料為CuZn15，鐵芯所用材料為50W600。為了精確測量并標記觸頭彈跳過程的動觸頭位移變化，使用Ke-Yence的LK-G150型激光位移器對上述電磁接觸器的一組觸頭進行實驗。激光位移器能夠實現位移數據的實時采集。為了充分掌握接觸器運行時的狀態，激光位移器需一直處于實時監測狀態。在測試過程中，讓其位移傳感器放置在接觸器的正上方，感測頭垂直對準該主觸頭進行零點標記。平臺主要布置如圖10所示。

圖10 實驗平臺布置圖Fig. 10 Layout of experimental platform

實驗所得的數據由電腦直接記錄，將Excel表格數據導入到MATLAB中進行1.2準則壞點剔除、間隔取樣值和散點函數曲線擬合。將標定取得的觸頭彈跳過程位移曲線與仿真得到的曲線進行對比，結果如圖11所示。

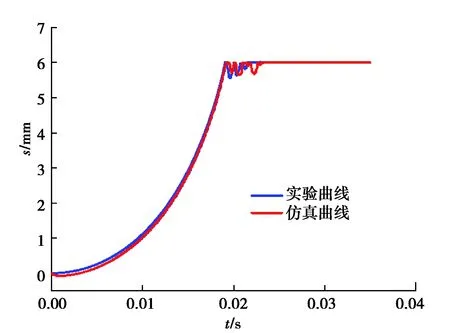
圖11 理論與實驗結果對比圖Fig. 11 Comparison of simulation and experimental results

由圖11可知，仿真曲線設定實驗測得交流接觸器動觸頭穩定閉合時間為19.71 ms，彈跳過程中的最大位移為0.284 1 mm；實驗得到的交流接觸器動觸頭穩定閉合時間為19.90 ms，彈跳過程中的最大位移為0.280 2 mm；得到：1)觸頭合閘時間誤差為0.96%；2)彈跳時間誤差為1.37%，且對于觸頭彈跳總時間和接觸器合閘閉合時間的實驗與理論相差都在2%以下，由此證明了該計算方法完全適用于交流接觸器彈跳特性的計算和分析。

6 結 論

通過對觸頭系統二自由度分段耦合微分方程進行化簡求值，對接觸器觸頭彈跳行為規律進行分析，利用ADAMS提供的接口，在ADAMS/View實現了遺傳算法程序的調用。進而得出以下結論：

1)動觸頭開始彈跳時間略早于動鐵芯，動觸頭彈跳的次數和最大位移均大于動鐵芯，觸頭初次碰撞時的最大位移較小，其碰撞時的最大位移出現于動鐵芯初次撞擊時刻。

2)通過AGA型算法優化后，接觸器合閘所需時間為23.32 ms，觸頭碰撞瞬間速度減小為1 187 mm/s，其彈跳過程中的最大位移為0.021 2 mm，彈跳總時間為0.32 ms，與優化前對比，觸頭彈跳時間和最大位移分別降低了89%和93%。

3)使用激光測距儀進行的實驗，理論與試驗結果誤差在2%以下，驗證了遺傳算法在交流接觸器設計應用中的可行性和有效性，研究結果為進一步全面優化接觸器樣機提供了新方法。