三角形中求范圍問題的解法
曹相波
(大理州實驗中學數(shù)學組 云南大理 671099)
一、問題引入
在解三角形中,我們經(jīng)常會碰到已知對邊對角求關(guān)于另兩邊的關(guān)系式的最值或取值范圍問題,比如求面積或周長的取值范圍。對于這類題,一般結(jié)合基本不等式可以解決,但利用不等式只能解決最大值問題,而最小值方向就需要其它知識解決,另外,如果當另兩邊前的系數(shù)不相等時的線性關(guān)系式求最值就不能簡單解決。

又△ABC中,a+c>b=2 ∴2<a+c≤4 ∴l(xiāng)=b+a+c=2+a+c∈(4,6]

從上例的解法,能看出基本不等式在求最大值方向問題不大,但對于求最小值方向就存在麻煩,需要結(jié)合其它隱含條件,比如,在求周長最小值方向時,需要考慮在三角形中兩邊之和大于第三邊這一隱含條件。那有沒有能直接求出最大和最小兩個方向的值呢?
二、問題探究
當然,在解三角形中,很多同學是正弦定理或余弦定理輪換使用來尋求解題方法,下面我們就用正弦定理嘗試一下。
解:由正弦定理可得:

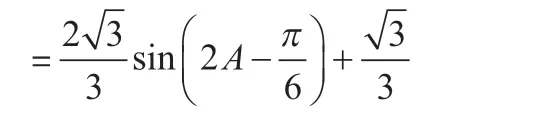
【注:三角函數(shù)中利用公式化簡是高中數(shù)學的基礎(chǔ),中間過程就留給讀者自行解決,以下也是如此】


從以上方法中可以看出,用正弦定理轉(zhuǎn)化到用角表示邊長之后,求三角形面積或周長問題就化歸到三角函數(shù)求最值問題上來,并且最大和最小方向的值都可以直接算出來。
三、問題變式
當然,有些時候題目條件可能會加強。比如在其它條件不變的情況下,將△ABC限定為銳角三角形時,求其面積S和周長l的取值范圍。銳角三角形這一條件的運用往往考慮最大角是銳角。
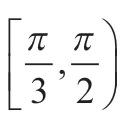

四、問題變式反思

那么,點B運動到什么位置時,△ABC的面積S和周長l取得最值?
借助于圓的對稱性,可知當點B與點M重合時,△ABC的面積S和周長l取得最大值;當點B無限接近于點A或點C時,△ABC的面積S和周長l趨近于最小值(為保證△ABC的存在,點B不能與點A或點C重合,故用趨近于一詞)。
在其它條件不變的情況下,將△ABC限定為銳角三角形時,則點B只能在點D和點E之間(點B不能和點D或點E重合)運動(AD和CE為直徑,∠CAE和∠ACD為直角)。

綜上,可以得到一個結(jié)果,△ABC的面積S和周長l都是在垂直平分于邊AC的直徑的端點M點處取得最大值。
五、方法推廣
從上面的數(shù)形結(jié)合分析能夠讓我們更加形象地理解題目的內(nèi)涵。基于對原題的深入理解我們就可以更好地利用這些思想方法去破解對應(yīng)的變式題。下面就對變式題型進行研究。
(一)已知角非60度

該題只對已知角大小做出改變,方法不變,用余弦定理結(jié)合基本不等式或者正弦定理用某個角表示未知邊轉(zhuǎn)化到三角函數(shù)求最值這兩個方法都可以(具體過程請讀者自行完成)。
另外,我們結(jié)合外接圓來研究一下。如圖2。

設(shè)兩腰長為x,則由余弦定理可得

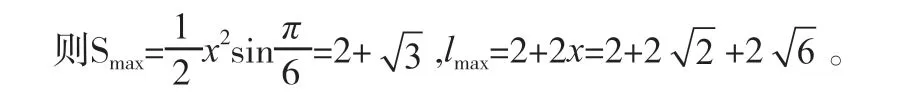
(二)求解另兩邊的一次關(guān)系式(xa+yc)的最值

解:由正弦定理得a,c與第二部分問題探究相同(故省略)
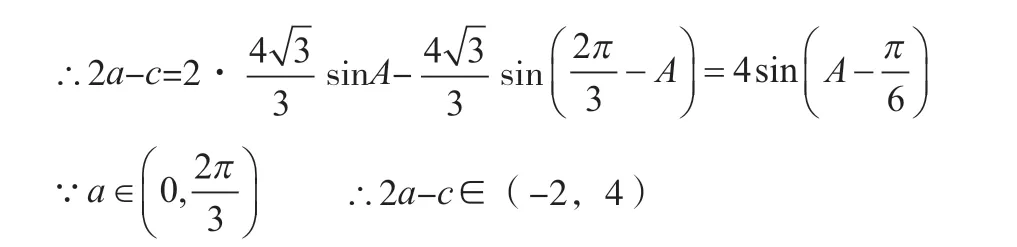
(三)已知非對邊對角
例題3:(2019年全國三卷第18題)
(1)求B; (2)若△ABC為銳角三角形,且c=1,求△ABC面積的取值范圍.
解:(1)過程略可得B=60°.

由于△ABC為銳角三角形,故 0°<A<90°,0°<C=120°-A<90°,所以30°<C<90°,

下面我們借助于圖形研究一下第二小題。
如圖3.由于△ABC為銳角三角形,則需考慮最大角為銳角即可。

當∠B=60°為最大角時,△ABC只能為等邊三角形,即為圖3中的△ABM。
當∠A為最大角時,點C在點M與點E之間運動(不包含點E和點M)。
當∠C為最大角時,點C在點M與點D之間運動(不包含點D和點M)。
綜上,當△ABC為銳角三角形時,點C在點D與點E之間運動(不包含點D和點E)。
由圖可得:S△ABD<S△ABC<S△ABE。
六、方法總結(jié)反思
從本文分析可以看出,相對于利用不等式求最值,利用正弦定理用角表示邊長從而轉(zhuǎn)化到三角函數(shù)求最值的方法更具有優(yōu)勢,更具有普遍適用性,可以稱作是解三角形求范圍問題的通法,當然結(jié)合外接圓來分析此類題目,讓我們更加形象地理解其內(nèi)涵。

