緊扣概念本質 優化變式教學
——以“平面向量的數量積”復習課為例
汪東生
(安徽師范大學附屬外國語學校城東校區 安徽蕪湖 241000)
數學復習課中,如何真正做到精講精練,提高復習效率,是數學老師所面對的一個重要課題。下面以一節高三數學復習課“平面向量的數量積”為例。通過對經典例題的挖掘,引導學生進行自主探究、變中生成的教學,希望對數學復習有所啟發。
一、課堂教學簡錄與反思
(一)課前練習

(二)課前思考
①求向量的數量積的方法有哪些?②向量的數量積有哪些應用?
二、一題多變,呈現知識網絡
例1 已知|a|=1,|b|=2,向量a與b的夾角60°,求a·(b-a)的值。
師:請同學們快速給出答案。
學生齊答:a·(b-a)=a·b-a2=0.
師:很好!通過本題,我們復習了向量數量積的公式:a·b=|a|·|b|cosθ.請再看下一題。
變式1 已知|a|=1,|b|=2,且向量a與b-a垂直,求向量a與b夾角。
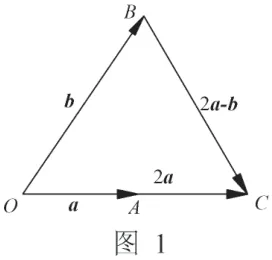
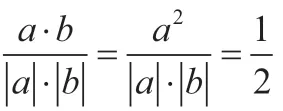
變式2 已知|a|=1,|b|=2,向量a與b的夾角60°,求向量a與2a-b的夾角。
生2:先求出|2a-b|=2和a·(2a-b)=1,再用公式求出其夾角為60°。
生3:畫圖,發現向量2a,b和2a-b構成一個正三角形,直接看出。
師:非常棒!向量本質是幾何概念,利用數學結合的方法快速解題。我們根據他這個圖你們能否求出向量a與2a+b的夾角?
學生齊答:30°
變式3 已知|a|=1,|b|=2,向量a與b的夾角60°,求 |2a-b|和|a+b|。
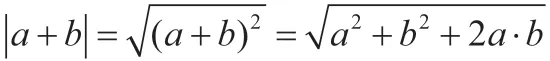
師:公式記憶很熟,在三角形中我們還可以用余弦定理求解|a+b|!再看題。

師:他是用向量數量積的公式。注意找兩向量夾角要平移使得它們共起點,那兩向量夾角范圍是?
學生齊答:0≤θ≤π!
師:如果本題∠O不是特殊角60°還行嗎?請再看下一題。
反思:通過課前練習,當堂投影學生作品蘇醒知識。然后從問題1出發,通過變式幫助學生復習了數量積定義、夾角公式、模長公式,通過數形結合體會向量數量積本質。
三、一題多解,使求解方法清晰
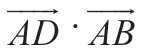
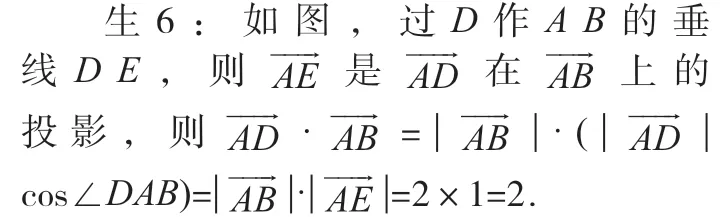
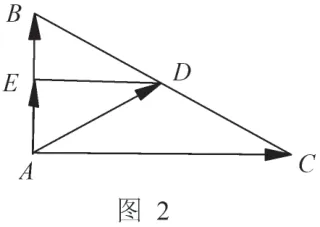
師:他對平面向量數量積的公式的本質理解了,他把兩個向量投影到一個向量上,用共線向量的長度來計算,我們把這種方法稱為投影法,當然還需要觀察兩個向量的夾角是銳角還是鈍角,以確定符號.誰還有其他方法?


學生根據題意說出選擇思路。
師:剛才同學們的這些解法,從不同的角度解決了這個問題,希望學生通過三種解法的比較,學會根據題目的特點,選擇最優的方法解題。
反思:通過例2、變式1、2的分析、講解、示范,學生可以清楚地知道求解向量數量積的分析和求解方法。考慮變式數量要“適度”,盡量避免題量展示解法展覽,減輕學生無效勞動,因此變式3、4讓學生說出思路即可。

