二重動力吸振器在汽車振動控制中的應用

李筱筱，陳藝夢

（長安大學汽車學院，陜西 西安 710064）

前言

隨著社會的發展，汽車已經成為主要的交通工具，人們對汽車乘坐舒適性的要求越來越高。汽車行駛過程中，因發動機或路面激勵造成的零部件共振是影響乘坐舒適性的主要原因。因此，對汽車振動的控制一直是各個企業以及國內外學者研究的重點。

傳統動力吸振器因簡單的結構、良好的減振性能在汽車振動領域得到廣泛應用。劉杰為降低某汽車發動機制動踏板抖動嚴重的問題，基于吸振器最有阻尼比關系設計了不同質量比的動力吸振器[1]。姜駿等人針對汽車方向盤抖動異常抖動的問題，設計了不同固有頻率的吸振器，并通過實驗分析吸振器的減振性能[2]。何山設計了一款結構簡單的動力吸振器，并將其應用于車輛副車架上，解決因副車架縱梁共振造成的車內后排噪聲過大的問題[3]。劉國政利用動力吸振器抑制某車輛驅動橋的振動，降低了車內噪聲[4]。趙健兵在汽車后背門上安裝吸振器，使因后背門共振造成的車內噪聲明顯降低[5]。

傳統動力吸振器雖然可以在其工作點有效抑制汽車零部件的振動，但是傳統動力吸振器減振頻帶窄，而且汽車激振頻率多變，可能使被控對象對于新的共振狀態，減振效果惡化。此時，若能降低被控對象頻率響應的共振峰，將有利于提升動力吸振器的工作性能。本文提出了二重動力吸振器，并分析了其減振性能。

1 傳統動力吸振器

汽車振動控制中通常在被控對象上安裝動力吸振器以降低被控對象的振動幅度。傳統動力吸振器相當于一個“質量-彈簧-阻尼”系統，安裝在單自由度主系統（即被控對象）的吸振器模型如圖1所示。

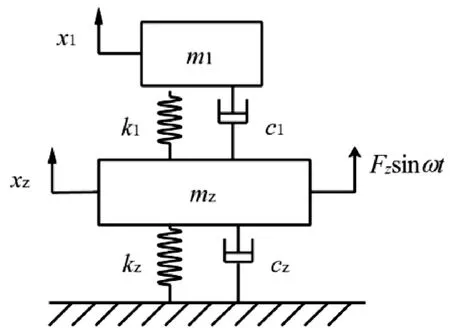
圖1 傳統動力吸振器模型

圖中，mz、kz、cz、m1、k1、c1分別表示主系統與吸振器的質量、剛度與阻尼系數；xz、x1分別表示主系統與吸振器的位移；Fzsinωt表示作用于主系統上的激振力，ω為外界激振頻率。對圖1中的模型進行分析，可得系統的動力學方程為：

引入吸振器與主系統質量比μ=m1?mz，吸振器與主系統固有頻率比γ=ω1?ωz，外界激振頻率與主系統固有頻率比λ=ω?ωz。其中主系統與吸振器固有頻率ωz與ω1分別為定義主系統阻尼比ξz與吸振器阻尼比ξ1分別為：ξz=cz? (2mzωz)，ξ1=c1?(2m1ω1)。將上述符號代入式（1）可得主系統頻率響應函數表達式為：

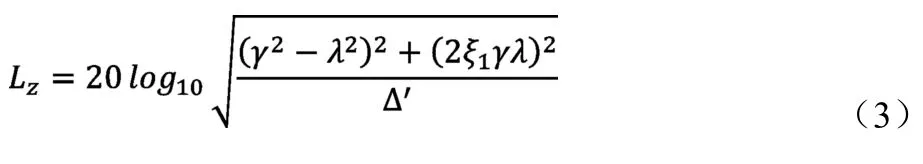
根據式（3）可做吸振器不同阻尼比時主系統頻率響應曲線，如圖2所示。

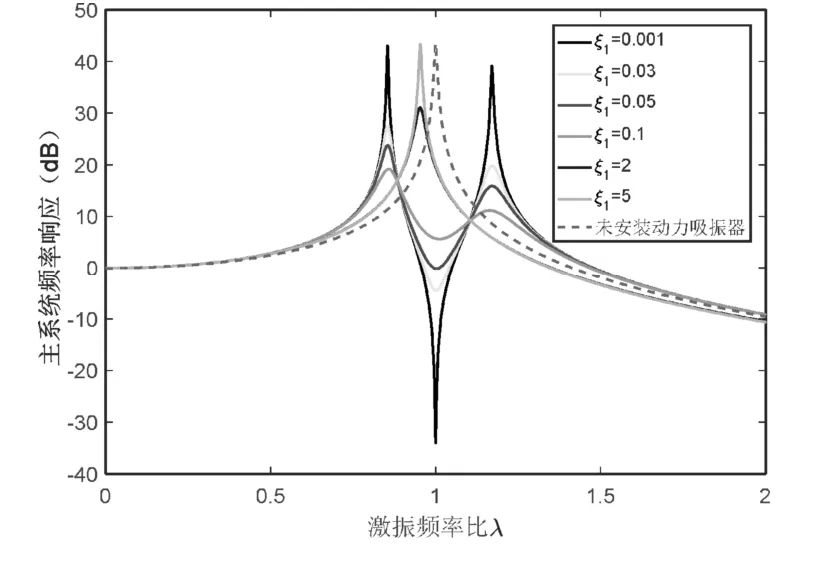
圖2 吸振器不同阻尼比時主系統頻率響應曲線

從圖2可以看出，當動力吸振器阻尼比ξ1很小（例如ξ1=0.001）時，吸振器減振效果好，但主系統頻率響應共振峰高。一旦激振頻率發生變化，主系統有可能發生共振。隨著吸振器阻尼比的增加，吸振器減振效果變差，同時主系統共振峰有所降低。當吸振器阻尼比很大時，吸振器相當于固定在主系統上，主系統頻率響應與不安裝動力吸振器時類似只有一個共振峰。在設計動力吸振器時通常要保證吸振器的減振效果的同時主系統共振峰又不能太高，吸振器的阻尼不宜過小。若能降低小阻尼吸振器的共振峰，則有利于提升吸振器的減振性能。為此本文提出了二重動力吸振器。

2 二重動力吸振器

2.1 二重動力吸振器建模

二重動力吸振器將兩個傳統動力吸振器組合使用，其中一個作為主吸振器減低主系統的振動，另一個則用來降低安裝動力吸振器后主系統共振峰，防止激振頻率偏移時，主系統出現過大振動。二重動力吸振器模型如圖2所示。將兩個動力吸振器分別記為吸振器1與吸振器2。

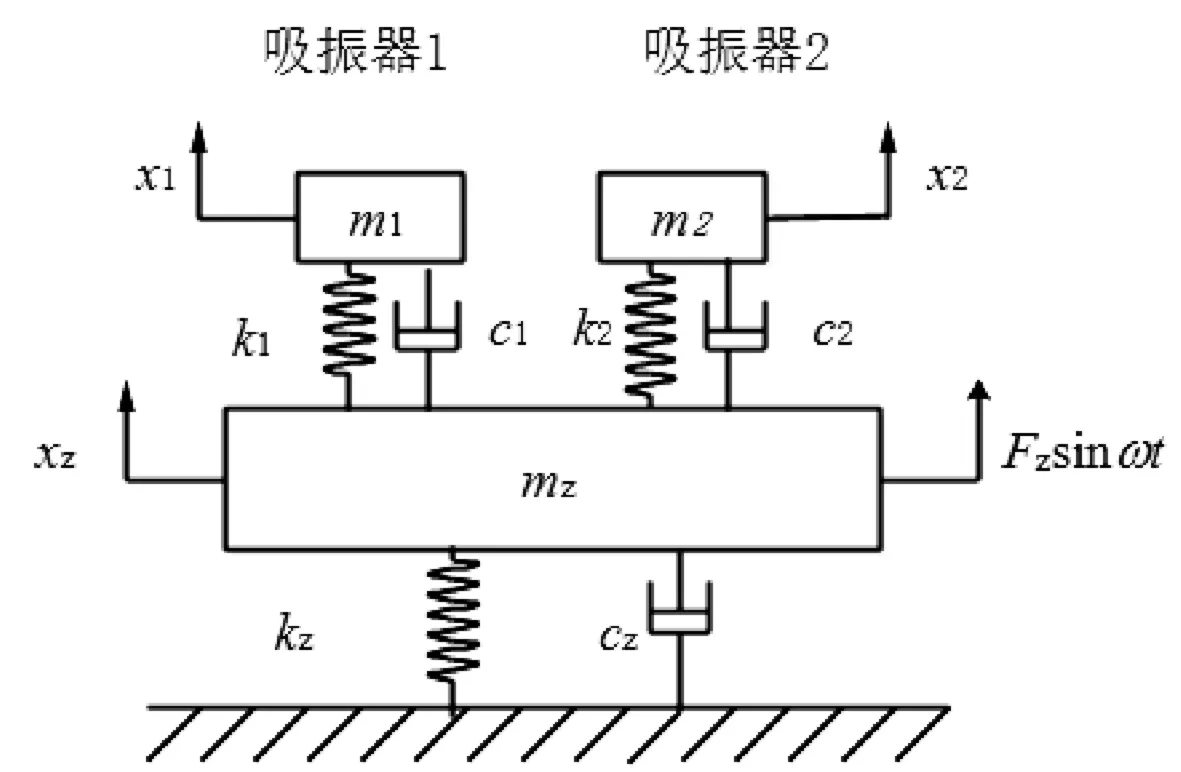
圖3 二重動力吸振器模型

圖中mz、m1、m2分別表示主系統與吸振器的質量；kz、k1、k2分別表示主系統與吸振器的剛度；cz、c1、c2分別表示主系統與吸振器的阻尼系數；Fzsinωt表示作用于主系統上的激振力，ω為外界激振頻率。根據牛頓定理可得二重吸振器模型的動力學方程為：

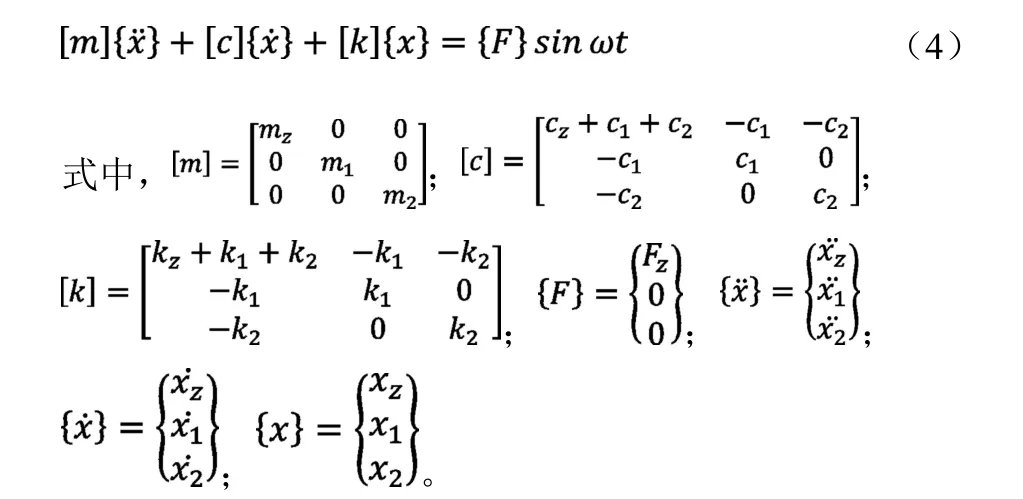
求解式（4）可得安裝二重動力吸振器的主系統頻率響應函數為：

2.2 二重動力吸振器減振性能

傳動動力吸振器的減振效果受吸振器阻尼的影響。在此假設吸振器1固有頻率小于吸振器2固有頻率，根據式（5）分析吸振器不同阻尼比ξ1與ξ2對主系統頻率響應的影響，如圖4與圖5所示。其中ξ1=c1?(2m1ω1)；ξ2=c2?(2m2ω2)。

從圖4可以看出，隨著吸振器1阻尼比ξ1增加，其固有頻率處減振效果變差，但是主系統頻率響應的共振峰均有所下降。從圖5可以看出，隨著吸振器2阻尼比ξ2的增加，其固有頻率處減振效果變差，主系統第二與第三個共振峰降低，但是吸振器2阻尼比的變化對主系統第一個共振峰影響不大。二重吸振器中一個吸振器阻尼比的變化，不會影響另一個吸振器固有頻率處的減振效果。當吸振器1有較大阻尼比時（例如ξ1=0.1）主系統共振峰峰值較低。

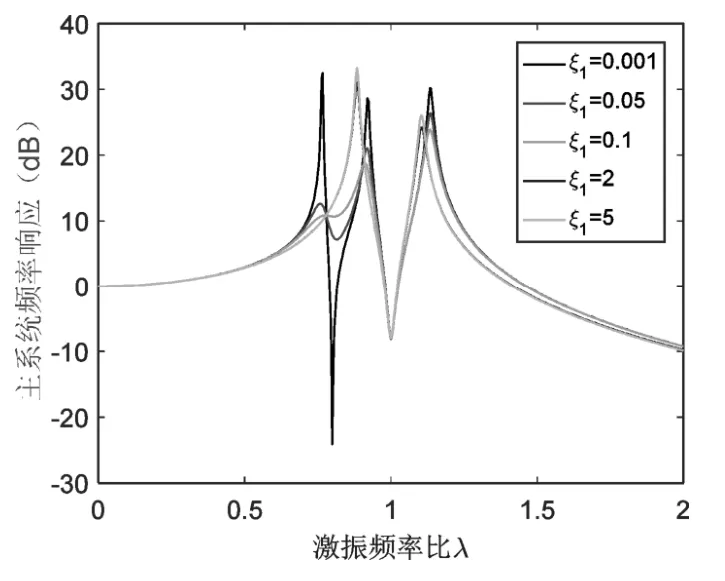
圖4 吸振器1阻尼對主系頻率響應的影響

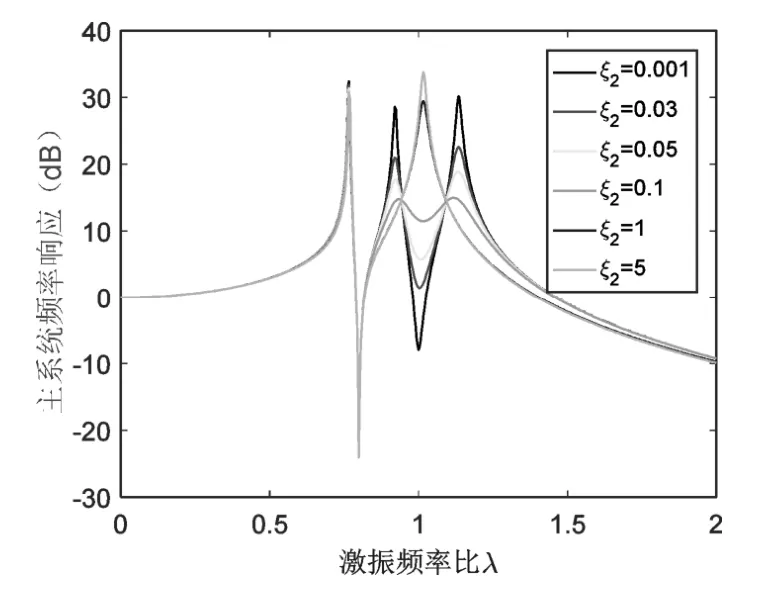
圖5 吸振器2阻尼對主系頻率響應的影響

二重動力吸振器中，若以固有頻率大的吸振器作為主吸振器，使其具有小阻尼以獲得良好的減振效果；另一個吸振器具有較大的阻尼系數以降低主系統共振峰。那么二重吸振器具有良好減振效果同時主系統共振峰有較低。為對比二重動力吸振器與傳統動力吸振器的減振效果，假設吸振器2結構參數與傳統動力吸振器相同，作安裝二重動力吸振器與僅安裝傳統吸振器時主系統的頻率響應，如圖6所示。圖中，紅色對應傳統動力吸振器，黑色對應二重動力吸振器。

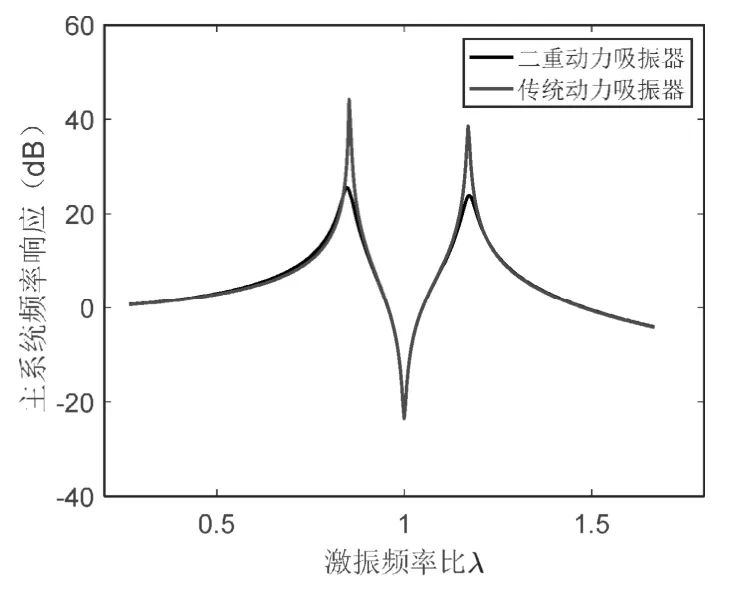
圖6 二重動力吸振器與傳統動力吸振器對比

從圖6可以看出，二重動力吸振器與傳統動力吸振器減振效果相同，但是二重動力吸振器對應的主系統共振峰更低。這就意味著，即使汽車行駛過程中，因發動機或者路面所造成的激振頻率發生變化，安裝二重動力吸振器的零部件處于共振時的振動幅度較安裝傳統動力吸振器的零部件振動幅度低，不會引起新的共振問題。

3 仿真與分析

根據前文分析，在二重動力吸振器中令固有頻率較小的吸振器（吸振器1）具有較大的阻尼比（阻尼比為0.1），同時固有頻率較大的吸振器（吸振器2）具有較小的阻尼系數；吸振器1固有頻率為0.8ωz，其中為ωz主系統固有頻率；吸振器2固有頻率與ωz相等。主系統與吸振器結構參數如表1所示。驗證二重動力吸振器的減振效果，在MATLAB/Simu- link軟件中搭建二重動力吸振器模型與傳統動力吸振器模型。其中傳統動力吸振器與二重吸振器中吸振器2參數相同。

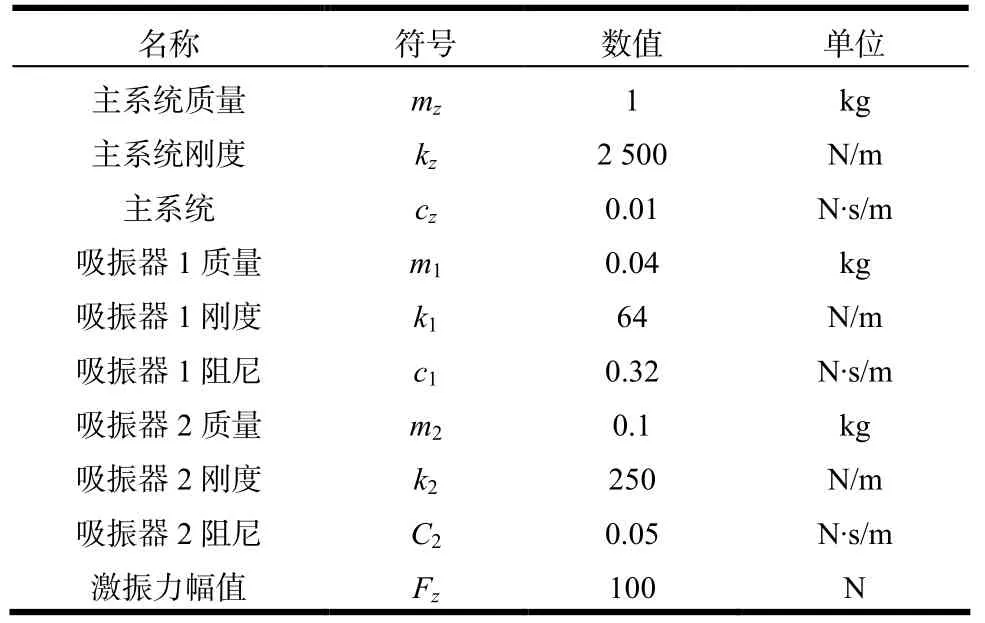
表1 主系統與吸振器參數

從表1可知主系統的固有頻率為50 rad/s。令激振頻率ω在0～10 s內從0 rad/s逐漸增加到50 rad/s。利用搭建好的模型仿真安裝二重動力吸振器與僅安裝傳統動力吸振器的主系統位移變化，如圖7與圖8所示。

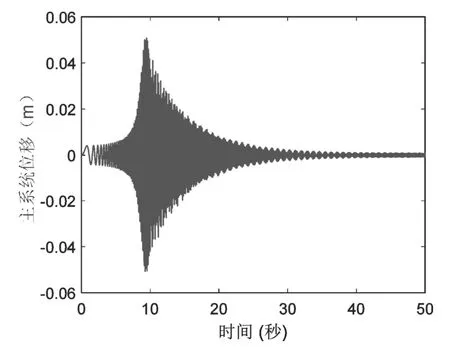
圖7 安裝傳統動力吸振器對應的主系統位移

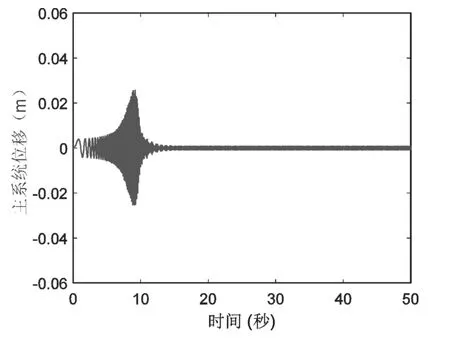
圖8 安裝二重動力吸振器對應的主系統位移

從圖7可以看出，0~10 s時，激振頻率ω從0 rad/s逐漸增加至50 rad/s，僅安裝傳統動力吸振器的主系統振動幅度逐漸增大至0.058 m。10 s~50 s激振頻率ω=50 rad/s，此時激振頻率與吸振器固有頻率相同，主系統振動幅度逐漸降低。大約30 s時，主系統處于穩態振動。從圖8可以看出，0~10 s時，隨著激振頻率ω從0 rad/s增大到50 rad/s，僅安裝二重動力吸振的主系統振動逐漸增大，最大振動幅度為0.0258 m。10 s~50 s激振頻率ω=50 rad/s，此時ω與二重動力吸振器中吸振器2固有頻率相同，主系統振動迅速衰減。大約15 s系統達到穩定狀態，且穩態振幅與安裝傳統動力吸振器的主系統穩態振幅相同。

對比圖7與圖8可以發現，當激振頻率逐漸增大至主系統固有頻率的變化過程中，安裝二重動力吸振器的主系統振動幅度較僅安裝傳統動力吸振器的主系統振動幅度明顯更低。因為二重動力吸振器中阻尼較大，主系統可以更快的達到穩態振動。所以與傳統動力吸振器相比，含有阻尼較大吸振器的二重動力吸振器工作性能更好。

4 結論

在汽車振動領域，激振頻率ω通常在較大范圍內變化。雖然安裝傳統動力吸振器后，激振頻率與吸振器固有頻率相等時可以有效抑制零部件的共振，但吸振器的安裝會使零部件產生新的共振峰。當激振頻率變化時有可能使零部件再次處于共振點。本文對提出的二重動力吸振器進行建模、求解，并分析吸振器阻尼對主系統頻率響應的影響，據此設計二重動力吸振器參數。在MATLAB/Simulink軟件中搭建二重動力吸振器模型與傳統動力吸振器模型，對吸振器的性能進行仿真。仿真結果表明：

（1）當二重動力吸振器中固有頻率較大的吸振器與傳統動力吸振器結構參數相同，在激振頻率變化時，二重動力吸振器對應的主系統共振峰更低；

（2）激振頻率處于吸振器減振點時，二重動力吸振器表現出與傳統動力吸振器相同的減振效果。

本文僅根據理論分析設定二重動力吸振器的結構參數，未通過優化結構參數提升二重動力吸振器的工作性能；仿真的方式驗證二重動力吸振器較傳統動力吸振器性能的改善，并未將二重動力吸振器應用到汽車具體零部件振動的控制中，需要在今后的工作中不斷完善。