混沌精英哈里斯鷹優化算法

湯安迪，韓 統，徐登武，謝 磊

（1.空軍工程大學研究生院，西安 710038；2.空軍工程大學航空工程學院，西安 710038；3.94855部隊，浙江衢州 324000）

0 引言

群智能優化算法是一種模擬自然界生物行為和自然現象的元啟發式算法，具有良好的并行性和自主探索性。自1975年美國教授Holland［1］根據達爾文進化論以及自然界優勝劣汰機制提出了遺傳算法以后，越來越多的學者通過對不同生物種群和物理現象進行分析，從中獲取靈感，提出多種群智能優化算法。如：Mirjalili等［2］根據座頭鯨的狩獵方式提出的鯨魚優化算法（Whale Optimization Algorithm，WOA）；Karaboga等［3］根據蜜蜂采蜜機制提出的人工蜂群（Artificial Bee Colony，ABC）算法；Yang［4］基于螢火蟲閃爍行為提出的螢火蟲算法（Firefly Algorithm，FA）；Jiang等［5］基于天牛覓食原理提出的天牛須搜索（Beetle Antennae Search，BAS）算法；Mirjalili等［6］受灰狼群的等級制度和捕食行為所啟發提出的灰狼優化（Grey Wolf Optimization，GWO）算法；Li等［7］根據病毒通過宿主細胞在細胞環境中生存和繁殖的擴散和感染策略提出的病毒群體搜索（Virus Colony Search，VCS）算法。

哈里斯鷹優化（Harris Hawks Optimization，HHO）算法是Heidari等［8］于2019年提出的一種新型群體算法，該算法啟發于哈里斯鷹捕食行為的探索、探索與開發的轉換、開發這三個階段，具有原理簡單、參數較少、全局搜索能力較強等特點，因此HHO已在圖像分割［9］、神經網絡訓練［10］、電機控制［11］等領域進行運用。但是HHO與其他群智能優化算法一樣，在求解復雜優化問題時，存在收斂速度慢、尋優精度低、易陷入局部最優等缺陷。為此Qu等［12］利用信息交換機制增強種群多樣性；Zhang等［13］引入指數遞減策略更新能量因子；Elgamal等［14］引入模擬退火機制。本文針對算法存在的問題，從以下四個方面進行改進：1）引入精英等級制度策略，利用優勢種群信息，增強種群多樣性，提升算法收斂速度和精度；2）使用Tent混沌映射調整HHO參數；3）使用一種新的能量因子更新策略，平衡算法的開發與探索；4）使用高斯隨機游走策略，對當前最優個體進行隨機擾動，增大搜索區域，并且當算法停滯時，對種群施加擾動，幫助算法跳出局部最優。

1 哈里斯鷹優化算法

哈里斯鷹優化算法是一種元啟發式算法，靈感來自哈里斯鷹的協作覓食行為。哈里斯鷹是發現于美國亞利桑那州南部的猛禽，它們在包括追蹤、圍攻和攻擊在內的幾個階段高效地執行協作覓食。每個階段的具體描述如下。

1.1 探索階段

在這個階段，哈里斯鷹隨機棲息在一些地點，通過敏銳的眼睛跟蹤和探測獵物，并以兩種機會均等的策略進行狩獵。

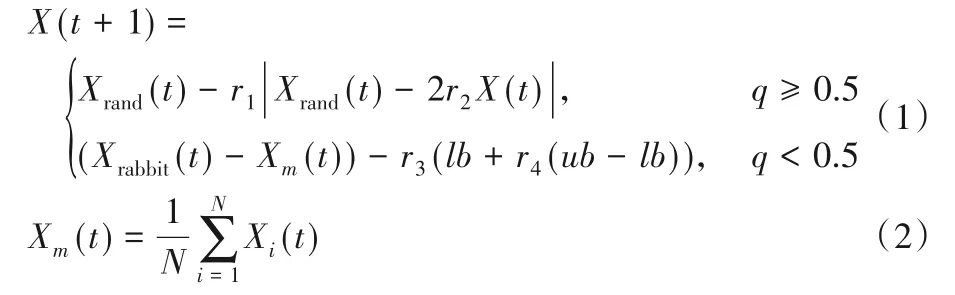
其中：Xrand為當前種群中隨機選擇個體，Xrabbit為當前最優個體，Xm為當前種群的平均位置，r1、r2、r3、r4均為0～1的隨機數，ub和lb分別為種群的上下界，N為種群數量。

1.2 探索到開發的轉換

哈里斯鷹從全局搜索轉向局部搜索主要依靠逃逸能量因子E來控制，計算公式如下：

其中：E0為-1～1的隨機數，t為當前迭代次數，T為最大迭代次數。

1.3 開發階段

在找到目標獵物后，哈里斯鷹會在獵物周圍形成一圈圍攻，等待突然襲擊的機會。然而，實際的捕食過程是復雜的，例如，被圍困的獵物可能會逃脫包圍的圈子。哈里斯鷹可以根據獵物的行為作出必要的調整。為了更好地模擬狩獵行為，開發階段使用四個策略進行更新，并通過參數E和一個0～1的隨機數來決定使用哪個策略。

1.3.1 軟包圍

當|E|≥0.5和r≥0.5時，獵物有足夠的能量，試圖通過隨機的跳躍逃出包圍圈，但最終無法逃脫，因此哈里斯鷹使用軟包圍的方式進行狩獵，公式如下：

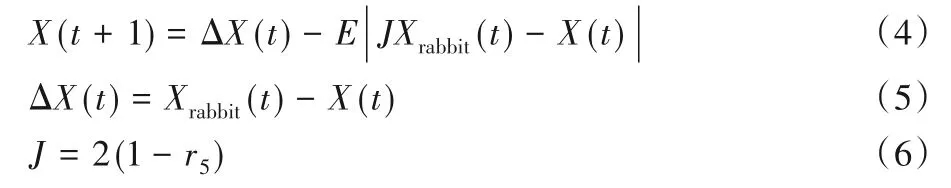
其中：ΔX為最優個體和當前個體的差值，r5為0～1均勻分布的隨機數，J為兔子逃跑過程中的跳躍距離。

1.3.2 硬包圍

當|E|<0.5和r≥0.5時，獵物既沒有足夠的能量擺脫，也沒有逃脫的機會，因此哈里斯鷹使用硬包圍的方式進行狩獵，公式如下：

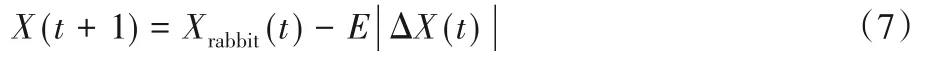
1.3.3 使用漸進式快速俯沖的軟包圍

當|E|≥0.5和r<0.5時，獵物有機會從包圍圈中逃脫，且逃逸能量足夠，因此哈里斯鷹需要在進攻前形成一個更加智能的軟包圍圈，通過以下兩個策略實施。當第一個策略無效時，執行第二個策略。

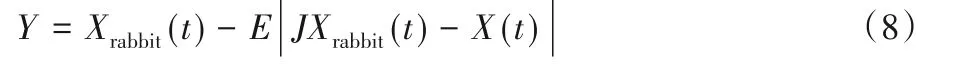
第二個策略更新公式為：

其中：D為問題維度，S是一個D維的隨機向量，LF為Levy飛行函數，公式如下：

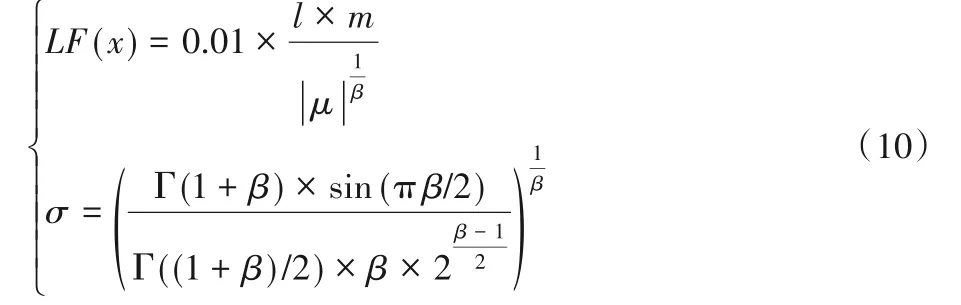
其中：l和m為0～1均勻分布的隨機數，β是取值為1.5的常數。因此該階段更新策略最終如下：

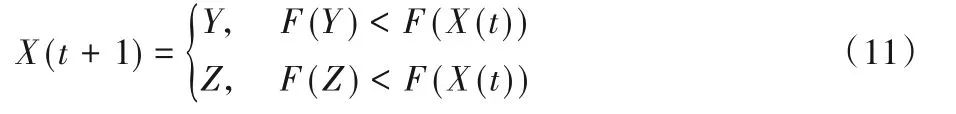
1.3.4 使用漸進式快速俯沖的硬包圍

當|E|<0.5和r<0.5時，獵物有機會逃逸，但逃逸能量不足，因此哈里斯鷹在突襲前形成一個硬包圍圈，縮小它們和獵物的平均距離，采用以下策略進行狩獵：

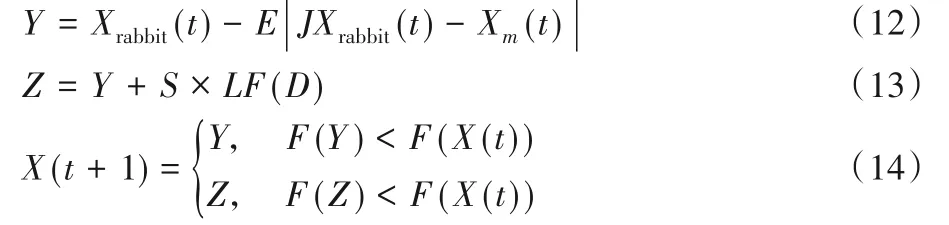
綜上所述，基本HHO算法流程如圖1所示。

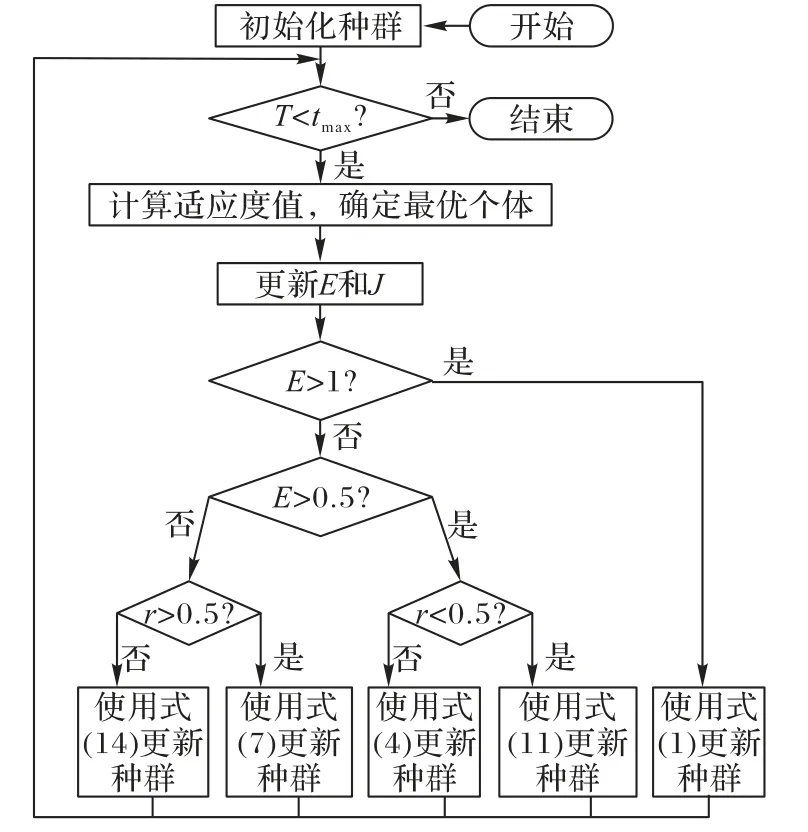
圖1 HHO算法流程Fig.1 Flow of HHO algorithm

2 混沌精英哈里斯鷹優化算法

同其他群智能優化算法類似，HHO算法也存在一定局限性。首先算法在迭代過程中種群僅利用最優個體信息，沒有與其他個體交流，導致多樣性下降；其次HHO算法易于陷入早熟，無法跳出局部最優；第三，HHO算法控制開發和探索過程的能量因子E的是線性變化的，而HHO算法的搜索過程是非線性變化。因此本文采用以下策略來改善HHO算法性能：引入精英等級制度策略，加強種群間交流，充分利用優勢種群來估計種群較好的進化方向，增強算法種群多樣性；使用Tent映射調整算法參數；針對能量因子E的迭代，引入新的更新公式，平衡算法的探索和開發能力；對最優個體使用高斯隨機游走策略，增大算法搜索區域，當算法陷入停滯時，利用高斯隨機游走策略增加種群個體多樣性，幫助算法跳出局部最優；最后采用貪婪策略充分保留優勢個體，加快收斂。

2.1 精英等級制度

HHO和其他智能算法一樣，在求解復雜問題優化時，存在迭代后期種群多樣性降低，易于陷入局部最優值，導致出現早熟現象、收斂精度不高。為了提高其全局搜索能力，避免后迭代期種群多樣性降低，引入一種精英等級制度，考慮迭代過程中加強次優解信息交流，選取三個最優位置來替代最優解，用以引導其余個體追隨。

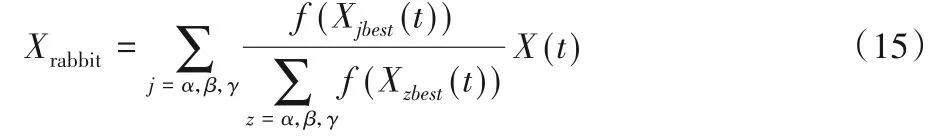
其中：Xjbest為當前種群優勢個體，f(Xjbest)為當前種群優勢個體適應度值。

2.2 Tent混沌映射

混沌映射具有隨機性、遍歷性和規律性的特點，多被用于產生算法的初始種群或者作為算法過程中的擾動［15-16］。本文提出利用Tent混沌映射調整哈里斯鷹算法的關鍵參數r的取值。r更新公式如下：

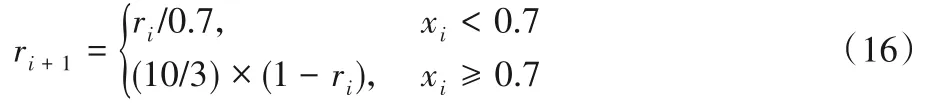
2.3 非線性逃逸能量更新策略

在基本HHO算法中，利用逃逸能量因子E1控制算法由全局搜索過渡到局部搜索，但能量因子E1的更新方式是由2線性減少到1，即迭代后半段，只進行局部搜索，易于陷入局部最優，為了克服算法后期只進行局部搜索的不足，提出一種新的能量因子E1的更新方式。

其中：t為當前迭代次數，tmax為最大迭代次數。從圖2可以得知：E在迭代前期較快下降，能夠控制算法全局搜索的能力；在迭代中期變化較緩，平衡全局搜索和局部搜索能力；在后期快速減小，加快局部搜索。E1在迭代整個過程都能進行全局搜索和局部搜索，且在前期主要進行全局搜索，后期在主要進行局部搜索的前提下保留了進行全局搜索的可能。

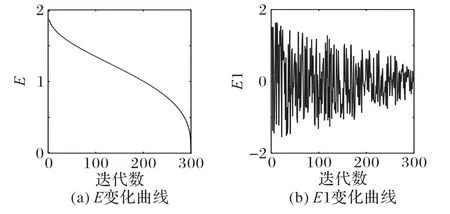
圖2 能量逃逸因子Fig.2 Energy escape factor

2.4 高斯隨機游走策略

在算法迭代尋優過程中，利用優勢種群的平均值來判斷算法是否陷入停滯，當優勢種群的平均值在連續兩次迭代過程中沒有變化，則認為算法陷入停滯，此時利用高斯隨機游走策略生成新個體，進而幫助算法跳出局部最優，克服早熟的不足。模型如下：

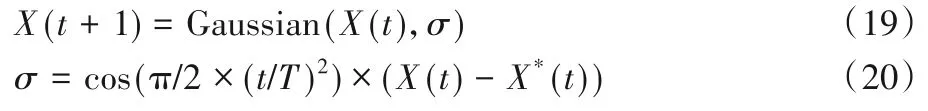
其中：X*為從優勢種群中隨機選擇的一個個體，引入一個余弦函數cos(π/2×(t/T)2)來調整高斯隨機游走的步長，通過余弦函數，在迭代前期施加較大擾動，迭代后期擾動迅速減小，進而平衡了算法的探索和開發能力。

最后使用貪婪策略，保證改進算法的全局收斂效率。混沌精英哈里斯鷹優化（Chaotic Elite HHO，CEHHO）算法的流程如圖3所示。

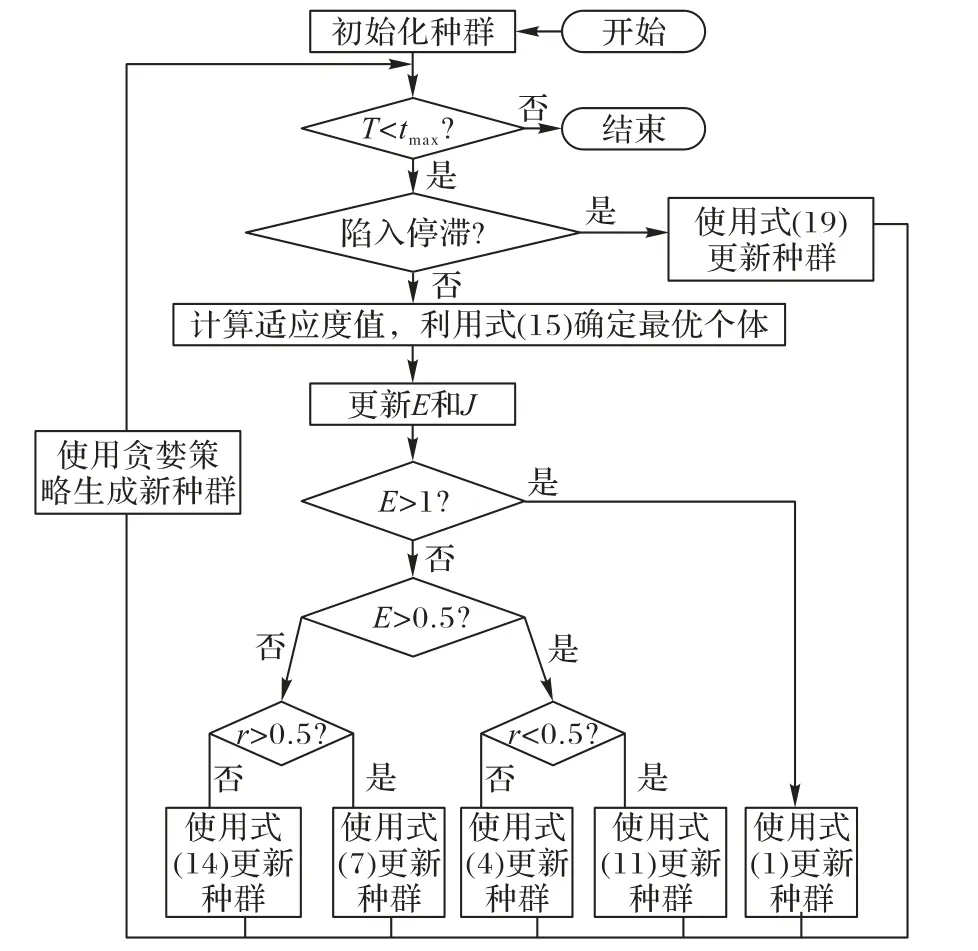
圖3 CEHHO算法流程Fig.3 Flowchart of CEHHO algorithm

3 CEHHO算法性能驗證

為了測試CEHHO算法的性能，使用20個基準測試函數進行測試。基準測試函數包括7個單峰測試函數、5個多峰測試函數和8個固定維度的多峰函數。F1～F7只有1個全局最優值，常用于評估算法的開發能力；F8～F20則可以評估算法的探索能力和局部最優規避能力。基準測試函數如表1所示。

3.1 實驗參數設置

為了充分驗證CEHHO算法的有效性與優越性，選擇WOA［2］、GWO［6］、PSO（Particle Swarm Optimization）［17］、BBO（Biogeography-Based Optimization）［18］以及傳統HHO算法進行對比分析。為公平比較，在相同實驗平臺上，設置種群數為50，最大迭代數為300，對比算法的其他參數與原文獻保持一致。所有算法均使用Matlab R2018b編程，計算機操作系統為Windows 10，處理器為AMD R7 4700U 16 GB。平均值用于衡量算法的求解精度，標準差用于衡量算法魯棒性，因此取平均值和標準差作為算法性能的度量標準。

3.2 實驗與結果分析

首先驗證改進算法在低維上的尋優能力，對表1中F1～F12在30維下進行獨立求解，F13～F20維數與表1中一致，記錄各算法獨立運行30次結果的均值和標準差，實驗結果如表2所示，其中粗體部分表示尋優結果最好的算法。

表1 基準測試函數Tab.1 Benchmark function

表2 不同算法的測試結果對比Tab.2 Comparison of test results of different algorithms

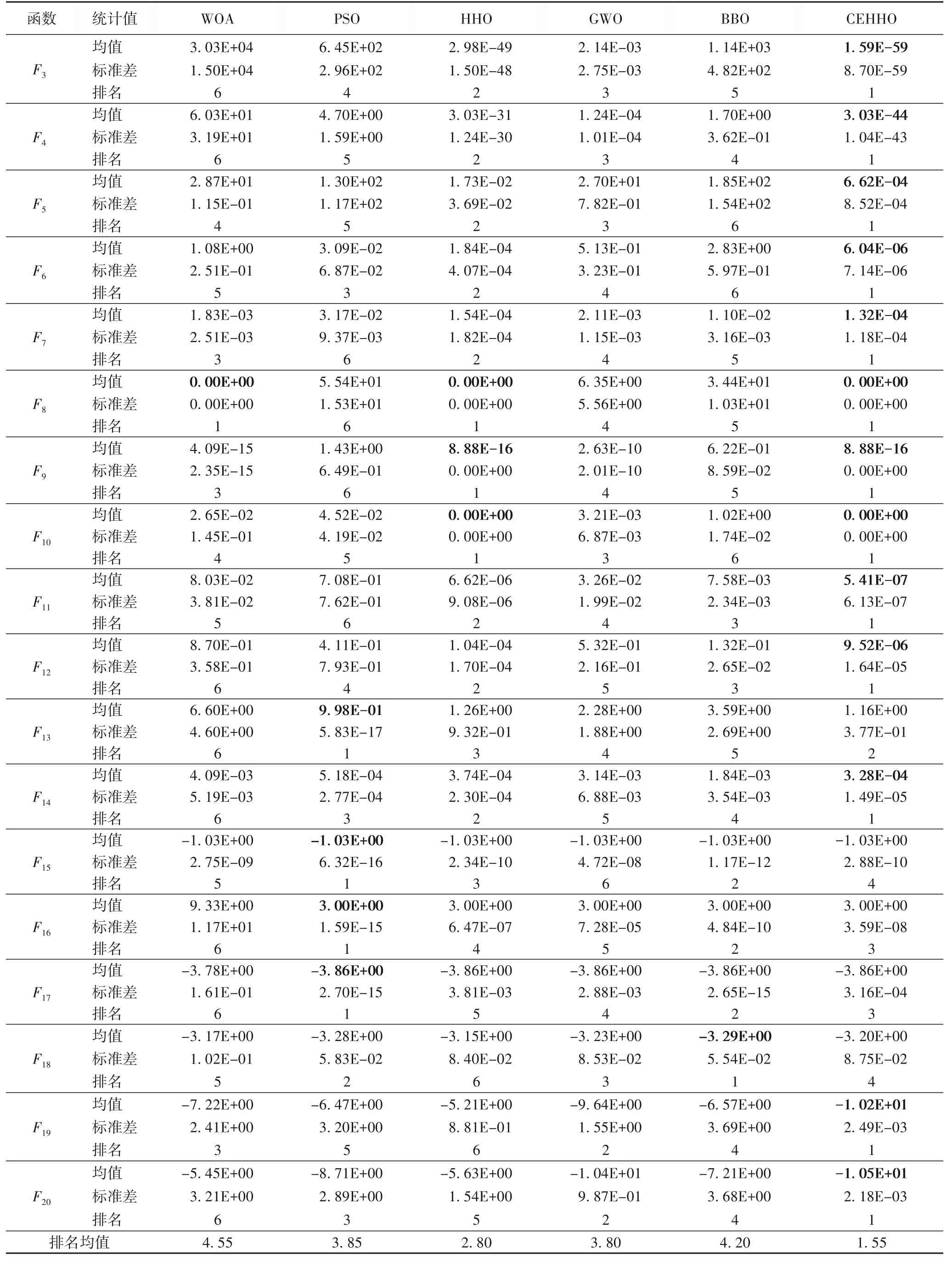
續表

由表2可知，對于所選測試函數，CEHHO算法的尋優能力明顯優于其他5種對比算法。在求解單峰測試函數F1～F7時，尋優效果最佳，且明顯優于HHO算法，其中F5的全局最小值位于一個拋物線型的山谷中，山谷曲面上的最速下降方向與到達全局最優值的方向近似垂直，且山谷內的值變化不大，大部分智能優化算法很難找到全局最優解，CEHHO在求解時明顯優于其他對比算法。整體上看，在求解單峰測試函數時，CEHHO尋優能力更強。對于多峰測試函數F8～F21，在求解F8時，CEHHO、HHO、WOA表現最佳；在求解F9～F11時，CEHHO優于4種對比算法；在求解F12、F14～F15和F19～F20時，CEHHO優于所有對比算法；在求解F13時，僅次于PSO，優于3種對比算法；在求解F16～F19時，所有算法性能相近，CEHHO穩定性較HHO更強，在求解F17～F18時，CEHHO表現一般，處于中間水平，但優于HHO。以上統計數據表明，在20個測試函數中，所提出的CEHHO在其中12個測試函數中，均優于所有對比算法，在2個測試函數中優于4種對比算法，在1個測試函數中優于3種對比算法，證明CEHHO尋優能力較強。

為進一步分析6種算法的尋優能力，根據表2的均值，對算法在各個測試函數的結果進行比較排序，結果如表2所示，表2最后一行為各算法的平均排序結果。CEHHO排序第1，尋優性能在6個算法中最強，且明顯優于HHO。其余算法排序為：HHO、GWO、PSO，BBO和WOA。

圖4為六種算法獨立求解基準測試函數30次所得結果的箱式圖，為了避免文章冗長，本文僅列出F1、F4、F9、F13、F14和F19，包含2個單峰測試函數、2個多峰測試函數和2個固定維度測試函數。表3為6組函數的四分位距（Inter Quartile Range，IQR）值，可以得知：在求解F1、F4、F9、F14和F19時，IQR值最小，說明CEHHO進行30次獨立求解的結果分布更加集中，并且CEHHO求得的異常點少于對比算法；在求解F13時，由IQR值可以得知CEHHO的分布不是最集中，但相對HHO，CEHHO的IQR更小，說明改進策略還是有效的。綜上，CEHHO的求解質量優于對比算法，且高質量解的數量也優于對比算法，驗證了本文算法具有良好的魯棒性。

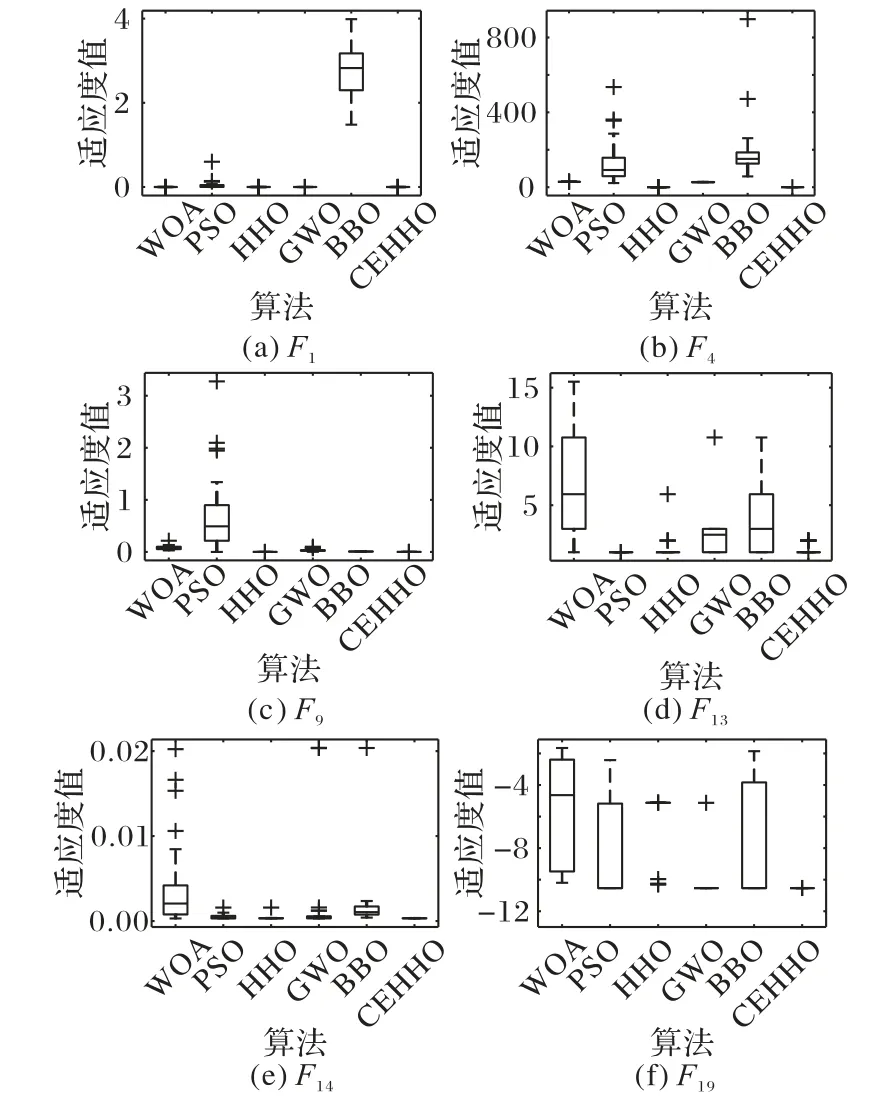
圖4 不同算法的收斂箱式圖對比Fig.4 Comparison of convergencebox plotsof different algorithms

表3 不同算法IQR值Tab.3 IQR of different algorithms

為了進一步闡述CEHHO的收斂性能，6種算法獨立運行30次求解20個基準測試函數收斂曲線如圖5，列出F1、F4、F9、F13、F14和F19的收斂曲線。在求解F5～F9、F11～F15、F19～F20時，CEHHO有更高的收斂速度和收斂精度；在求解F1～F4和F10時，CEHHO收斂速度在前期弱于HHO，但在犧牲一定的收斂速度的情況下，能夠在后期更快收斂到全局最優值，且收斂精度優于所有對比算法；在求解F16～F18時，收斂速度較對比算法表現不佳，但同樣能收斂到全局最優值。且CEHHO在所有測試函數中，其中14個測試函數的尋優性能明顯優于HHO算法，5個測試函數的尋優性能差距不大，但收斂速度快于HHO算法。此外，計算效率也是衡量算法性能的重要指標，因此表4列出了各算法30次求解各測試函數的耗時。可以看出，CEHHO雖然耗時不是最少，但其耗時低于基本HHO，考慮到尋優性能優于其余對比算法，因此在提升算法尋優性能的情況下，CEHHO的計算耗時也能接受。

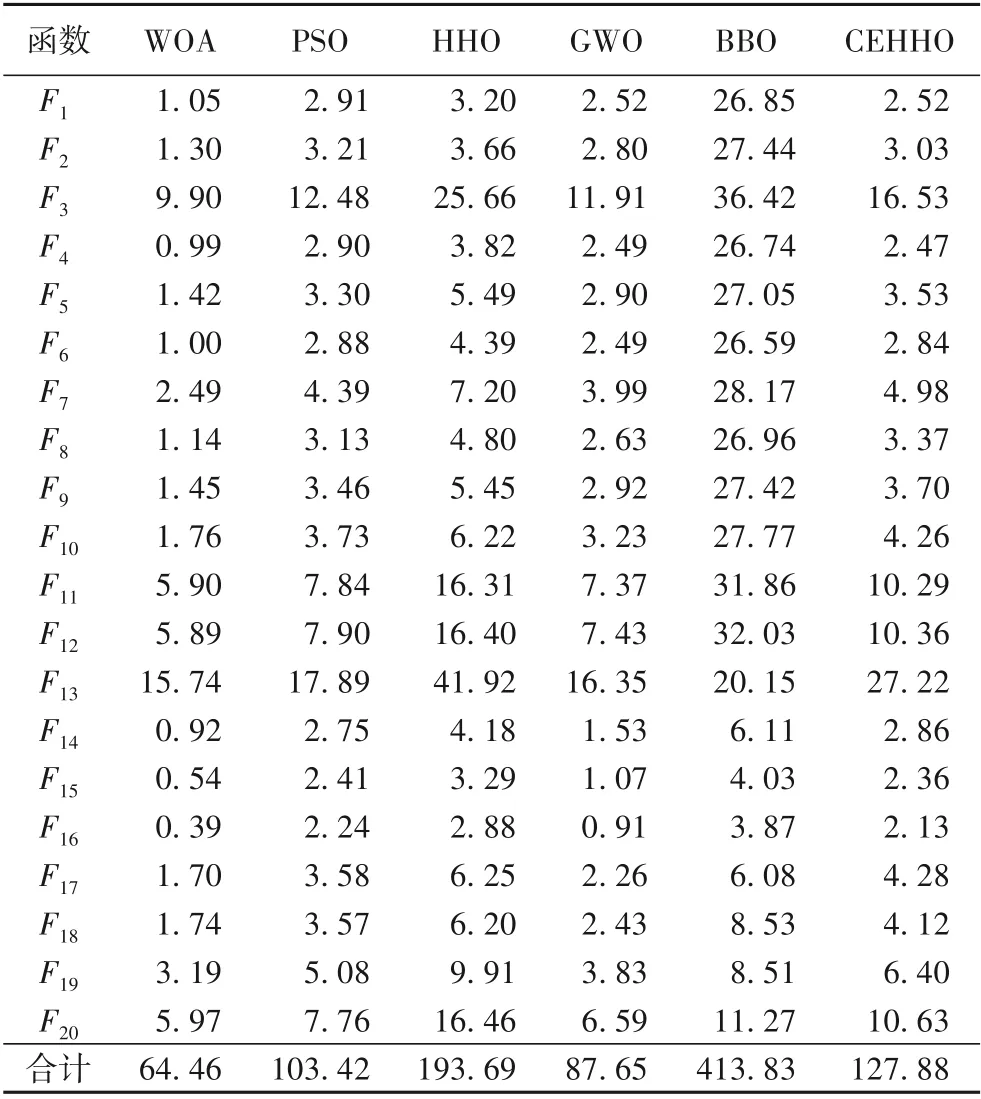
表4 不同算法的耗時對比 單位：sTab.4 Comparison of time cost of different algorithms unit：s

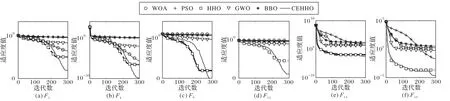
圖5 不同算法的收斂曲線對比Fig.5 Comparison of convergence curves of different algorithms

通過對30次獨立運行求解測試函數結果的平均值和標準差進行分析比較，并不能精確分析每次運行的結果，且在運行過程中仍有一定概率出現偶然，致使算法在均值上具有較好表現。因此在統計學層面上來判斷不同算法整體結果的顯著性區別，采用Wilcoxon統計檢驗。將6種算法獨立求解20個測試函數30次得到的結果作為樣本，在置信度為0.05的條件下進行檢驗，判斷5個對比算法所得結果與CEHHO所得結果的顯著性區別。當秩和檢驗的p值小于0.05時，說明兩種對比算法具有顯著性差異，否則說明兩種算法的尋優結果在整體上是相同的［19］。Wilcoxon統計檢驗p值結果如表5所示。

從表5可知，CEHHO在17個測試函數中與BBO和WOA有顯著區別，在19個測試函數中與PSO、GWO有顯著區別，在13個測試函數中與HHO有顯著區別。綜上，CEHHO在求解20個測試函數時，至少在一半以上的函數中與對比算法有顯著區別。因此基于統計學理論分析，CEHHO的尋優性能明顯優于6種對比算法。

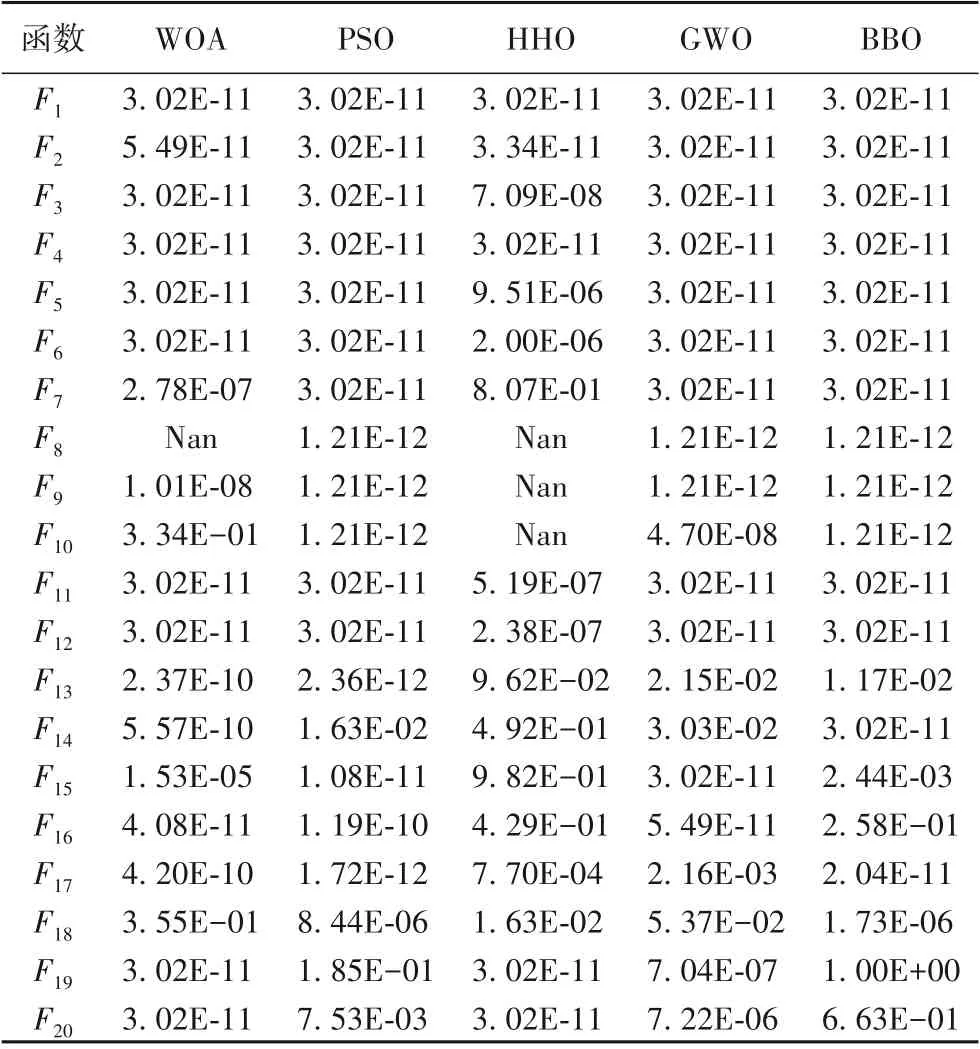
表5 不同算法的Wilcoxon統計檢驗結果Tab.5 Wilcoxon statistical test results for different algorithms

通過以上分析可知，CEHHO算法在低維函數上展現出了較強的尋優能力，但是一般算法在求解高維復雜函數問題時極易失效，而大部分實際優化問題都是大規模的復雜優化問題，因此，為了說明本文所提改進算法的實用性，將6種算法分別在50維和100維測試函數上進行對比，實驗結果如表6和表7所示。

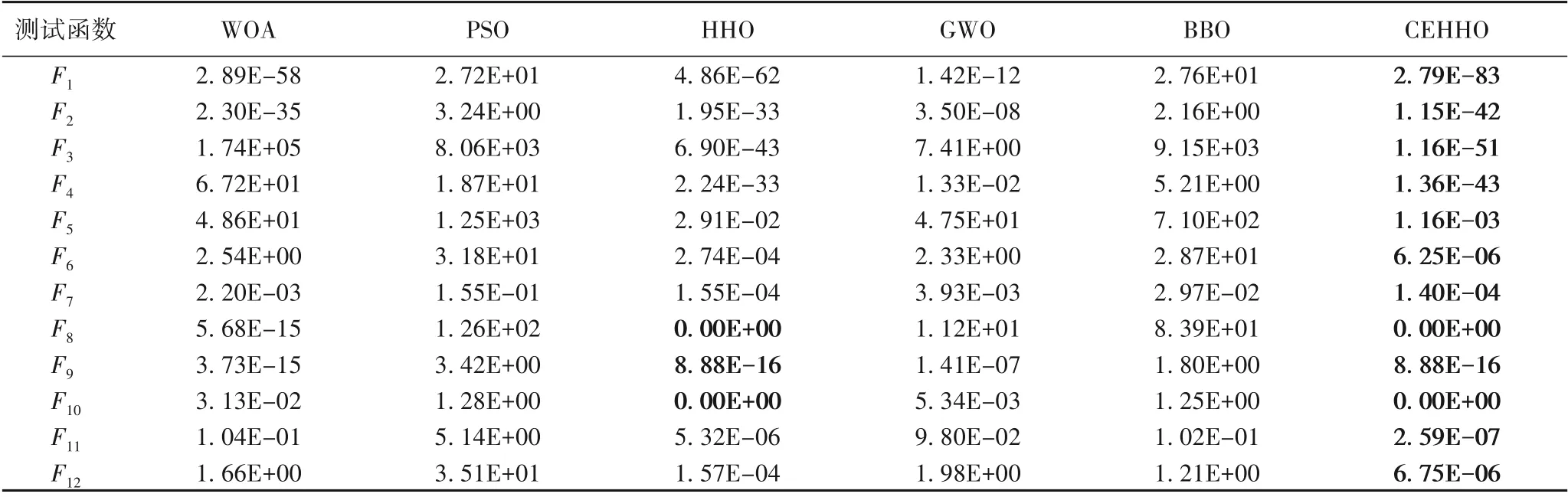
表6 求解F1～F12時不同算法測試平均值結果比較（50維）Tab.6 Comparison of mean test results of different algorithms in solving F1-F12（50D）

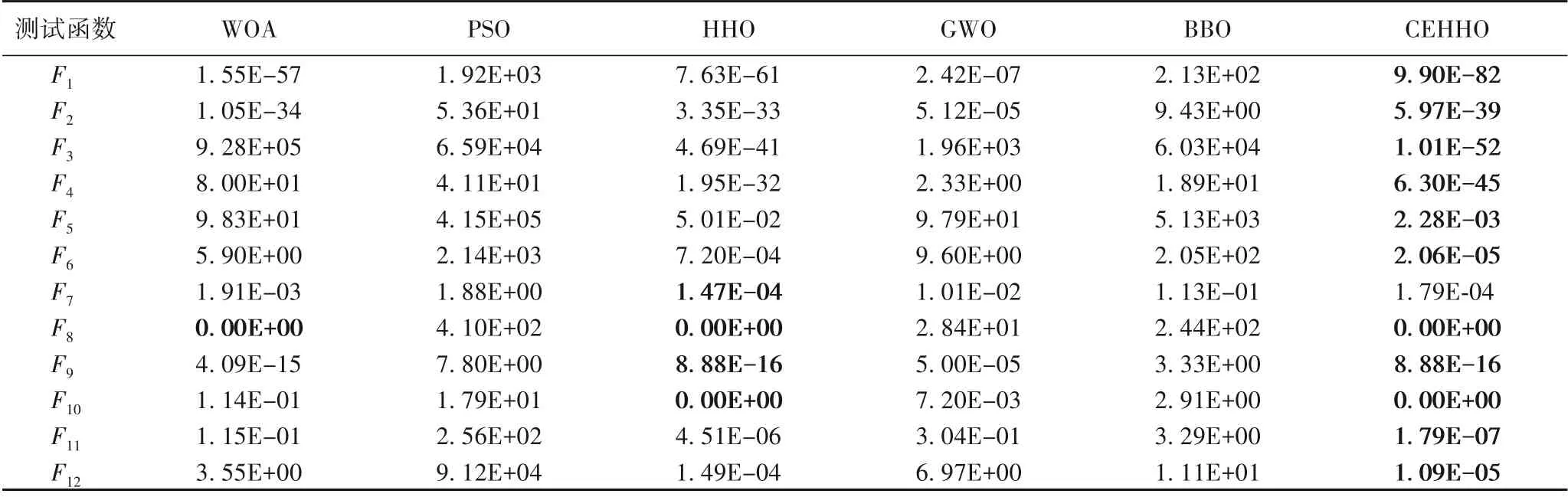
表7 求解F1～F12時不同算法測試平均值結果比較（100維）Tab.7 Comparison of mean test results of different algorithms in solving F1 to F12（100D）

綜合50維和100維測試函數平均值結果來看，在求解F8～F10時，CEHHO與HHO無明顯差異，CEHHO在求解F1～F7、F11～F12時，尋優性能優于所有對比算法，尤其是在高維條件下，對比算法尋優性能較為一般，而CEHHO能在高維條件下仍能有效進行尋優。

4 結語

本文針對基本HHO算法求解精度低、收斂速度慢以及易于陷入局部最優等問題，提出了一種融合精英等級制度策略的能量非線性更迭的混沌哈里斯鷹算法。改進算法利用精英等級制度，加強種群間信息交流，利用優勢種群估計更好的進化方向和求解范圍，增強種群多樣性，提升算法的尋優精度，避免陷入局部最優；使用Tent混沌映射控制算法關鍵參數，采用一種非線性的能量更新策略，提高算法的全局探索和局部開發能力；引入高斯隨機游走策略，在算法陷入停滯時，對種群進行隨機擾動，增強了算法在迭代后期跳出局部最優的能力；最后利用貪婪策略有效保留優勢種群，提高收斂速度。將CEHHO算法與基本HHO算法以及4種新型群智能優化算法在20個測試函數上進行實驗對比。結果表明，CEHHO在求解低維和高維函數、單峰和多峰函數優化問題時均表現出良好的尋優性能，具有較強的局部最優規避能力、更高的收斂速度和收斂精度。同時，改進算法在個別測試函數中運行時間較長，在一些固定維度測試函數上表現不是最佳。未來將針對這兩個問題進行研究，并將算法應用到無人機作戰任務規劃等實際工程領域中，驗證算法的實用性。