一類非線性混料指數模型及其最優設計

陳嘉麗, 張崇岐

(廣州大學 經濟與統計學院, 廣東 廣州 510006)

0 引 言

混料試驗設計[1-3]被廣泛應用于食品加工、化工、醫藥、農業等行業，越來越受到大家的關注. 怎樣保證估計量在精確性方面具有某種優良性質并且使試驗成本較低，從而更有效地選取設計點，是混料試驗設計的研究范疇. 目前的混料試驗設計多是建立在線性模型上，如Fedorov[4]、Cornell[5]、Mandal等[6]和 Sinha等[7]，這些模型可以用q變量系統的q階多項式模型來表示[8-9]：

β12…qx1x2…xq,

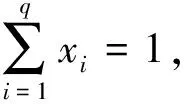
目前學者對線性混料模型研究甚多，研究手法較為成熟. 但實際應用中很多問題用線性模型去擬合總存在一定誤差. 因此，對非線性混料模型[10-11]的最優設計問題進行研究十分必要.由于非線性混料模型信息矩陣的逆求解過于復雜，從而衍生出的一種方法是將原本的非線性模型進行泰勒展開，使其轉化成常見的冪函數的線性模型. 此做法本質上解決的仍是線性問題，難免會產生一定的誤差，因此，有必要對非線性混料模型進行更為深入的探討. 2012年朱志彬等[12]基于becker模型提出了非線性分式混料模型, 并研究了二分量模型的 D-最優設計. 2015年張崇岐等[13]提出了一類含常數項的混料指數模型, 并直接在單純形格子點上研究了模型的D-最優設計. 本文提出一類特殊的混料指數模型, 通過在試驗域內多次迭代得到模型的D-最優設計，并用等價定理來證明該設計的D-最優性.

1 模型構造

實際生活中很多產品都是由多種物質混合制作而成的，如面包、藥品和飲料等. 不同成分之間占比的變化將會影響最終產品的質量. 為了生產出質量更佳的產品，得到最優的配料比例，減少成本，需要尋找最優混料試驗設計.

假設某產品有q種成分，它們在生產中的比例分別為x1,…,xq，顯然x1≥0,…,xq≥0，且x1+…+xq=1.故混料的試驗區域為

Sq-1={(x1,…,xq)|xi≥0,i=1,…,q,x1+…+xq=1}.

考慮一般的線性回歸模型,其基本形式為

y=βTf(x)+ε,

其中,y是響應變量,ε是隨機誤差,β=(β1,β2,…,βk)T是k維未知參數向量，f(x)=(f1(x),f2(x),…,fk(x))T為已知的關于設計點x=(x1,x2,…,xq)∈Sq-1的實值函數向量.一般假設

E(ε)=0,Var(ε)=δ2.

與線性回歸模型不同的是，非線性回歸模型G(x,β)的一般表達式如下：

y=G(x,β)+ε.

目前國內對非線性混料模型的研究較少，常見的非線性混料模型包括非線性混料指數模型和非線性分式可加混料模型，其中以非線性混料指數模型更為常見.

現考慮二分量非線性混料指數模型

實踐教學內容體系(表1)三個層次中，第一層次是基礎層次：通過英語聽說訓練，學生能熟練地運用英語進行簡單的英語交流；通過計算機實訓，讓學生掌握計算機的基本操作，能夠運用計算機進行單據的制作和文件處理。在學生學習專業課之前，帶領學生參觀當地的外貿企業，也可以邀請企業人士到學校為學生作報告，使學生對外貿業務流程有一個大體的認識，激發學生的學習熱情。

η=β1x1+β2eαx2+ε

(1)

其中,η是響應變量，β1,β2和α是待估參數，ε是均值為0、方差為σ2的隨機誤差，x1+x2=1.不失一般性，本文考慮當α=1時的情況：

η=β1x1+β2ex2+ε

(2)

就模型(2)討論它的D-最優性，顯然模型具有兩個未知參數，因此，必須找到一個兩點設計使其滿足D-最優性. 設在試驗區域X中的一個設計ξ為

其中，x1=(x11,x12),x2=(x21,x22)為不同的支撐點，0≤λ1,λ2≤1,λ1+λ2=1.記f(x)=(x1,ex2))T.

設計ξ所對應的信息矩陣M(ξ)為

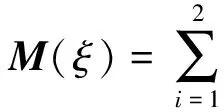
且與模型η相對應的方差函數為

d(x,ξ)=fT(x)M-1(ξ)f(x).

在混料試驗設計中，若存在設計ξ*使得信息矩陣的M(ξ)的行列式最大化，即

|M(ξ*)|=max|M(ξ)|,

稱ξ*為D-最優設計.

由等價定理可知，對連續回歸模型與緊致空間而言，ξ*稱為模型η的D-最優設計當且僅當ξ*滿足

2 主要結果

根據D-最優準則可知，D-最優設計是最小化|M-1(ξ)|或最大化|M(ξ)|的設計.首先計算出模型(2)在設計ξ下的信息矩陣

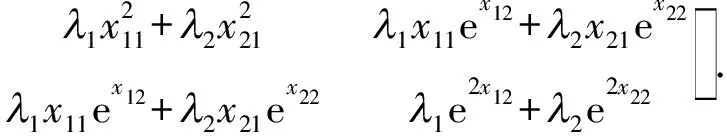
其次，計算設計ξ在模型(2)下的信息矩陣行列式

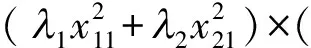
(λ1x11ex12+λ2x21ex22)2=

(λ1λ2)(x11ex22-x21ex12)2.

由約束條件λ1+λ2=1進一步可得

因此有

x21ex12)2.

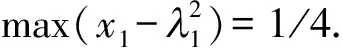
表1 f(x1,x2)函數的10組不同初始值計算結果

從表1可以知道，10組不同初始值對應的最終值都是(0,1)，且(x11ex22-x21ex12)2=1，迭代次數在20次左右，顯然另一設計點為(1,0).

此外，根據方程f(x1,x2)=(x1ex2-x2ex1)2，在區域0≤x1≤1,0≤x2≤1，用MATLAB畫出對應的三維立體圖形，從圖1中也可以得到在(0,1)和(1,0)時，max((x1ex2-x2ex1)2)=1.

圖1 f(x1,x2)函數的三維圖Fig.1 The three-dimensional graph of the function f(x1,x2)

由此可以得到模型(2)的D-最優設計

對于模型(2)，證明所得的設計ξ*是設計域上的D-最優設計.該設計的信息矩陣M(ξ)與它的逆M-1(ξ)

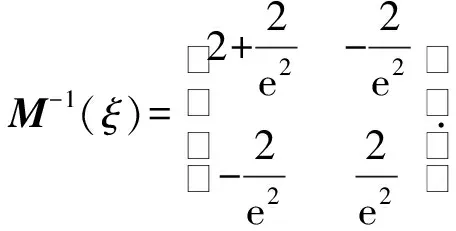
由此可得方差函數

d(x;ξ*)=fT(x)M-1(ξ)f(x)=

其中,0≤x1,x2≤1,x1+x2=1，通過MATLAB畫出d(x;ξ*)在區間[0,1]范圍的曲線圖，如圖2.

圖2 d(x;ξ*)的曲線圖Fig.2 The curve graph of d(x;ξ*)

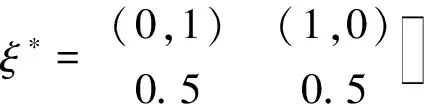
3 結束語

在各種不同的混料模型中，非線性混料模型因其在實際生活中存在廣泛的應用價值而成為當前研究熱點. 由于該模型計算非常復雜，算法效率低，沒有一套相對完善的理論，因此，需要進一步的深入研究. 本文以二分量非線性混料指數模型為基礎，通過多次迭代得到該模型的D-最優設計，并用等價定理來證明該設計的D-最優性. 在未來的研究中，可以考慮對更高階的非線性混料指數模型的最優設計問題做出進一步探討.