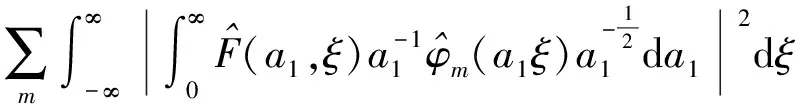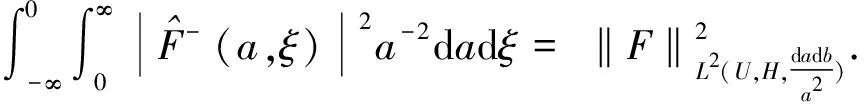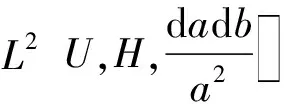Quaternionic-valued wavelet transform and orthogonal decomposition

-, -

(School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, China)

Abstract： In this paper, we study some properties of the quaternionic-valued wavelet transform in one dimension. The wavelet transform gives an isometric operator from the Hardy space (conjugate Hardy space) to L2 In addition, we obtain an orthogonal decomposition of L2 by using the properties for special functions.

Key words： quaternionic-valued function; wavelet transform; special function; orthogonal decomposition

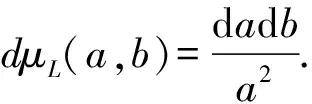
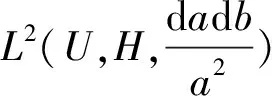
1 Preliminaries

In this section, we first recall fundamental facts of quaternions which can be found in Refs.[9-10]. Let

H={a+bi+cj+dk∶a,b,c,d∈R},

whereij=-ji=k,jk=-kj=i,ki=-ik=jandi2=j2=k2=-1.For anyq∈H, it can be written asq=a+ib+jc+kd=(a+ib)+j(c-id)=u+jv, then its conjugation is

Obviously, |q|2=|u|2+|v|2and (pq)C=qCpCfor ?q1,q2∈H,

wherefsatisfies

Letf(x)=f1(x)+jf2(x),g(x)=g1(x)+jg2(x)∈L2(R,H).The inner product·,·L2(R,H)is defined by

The quaternionic-valued function spaceLP(R,H) andL∞(R,H) is the set off(x)=f1(x)+jf2(x), wherefsatisfies

For anyF(x)=f1(x)+jf2(x)∈L2(R,H), we define the Fourier transform by

(

ξ

)

=

1

(

ξ

)+

j

2

(

ξ

),

ξ

∈

R

,

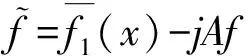
Now let us introduce natural convolution of quaternionic-valued functions. For anyf,g∈L2(R,H),

(fg)(x)=(f1*g1)(x)-(

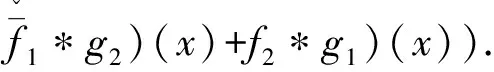
We know that it satisfies (fg)from Ref.[8]. By the above definition of quaternion convolution, we can naturally define the wavelet transform onL2(R,H).

Given an admissible waveletφ, the admissible wavelet transform is defined by

whereU={(a,b):a>0,b∈R}

Tφfis the continuous wavelet transform of a square integrable complex valued functionfonR, this definition comes from Ref.[8].

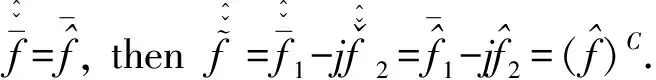
2 Some properties of quaternionic-valued wavelet transform

In Ref.[8], Akila, et al. obtained Parseval’ identity for quaternionic-valued wavelet transform. Iff,g∈L2(R,H),

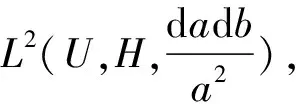
(1)

If wavelet functionφsatisfies Eq.(1), we sayφis an admissible wavelet.

Theorem 1 Letf,g∈L2(R,H),φ,ψ∈L2(R,H) are admissible wavelets. Then, we have

(1) (Linearity)

[Wφ(μf+γg)](a,b)=μ[Wφf](a,b)+γ[Wφg](a,b),

[Wμφ+γψf](a,b)=[Wφf](a,b)μC+[Wφf](a,b)γC, ?μ,γ∈H.

(2) (Translation)

[Wφf(·-x0)](a,b)=[Wφf](a,b-x0),

[Wσx0φf](a,b)=[Wφf](a,b+ax0), whereσx0φ(x)=φ(x-x0).

(3) (Scaling)

(4) (Parity)

[W](a,b)=[Wφf](a,-b), where(x)=f(-x).

Proof We only give the proof of (3), and other proofs are analogous.

[Tφ1f1(c·)](a,b)=

[TDcφ1f1](a,b)=

Lemma 1[11]Let {aj} be a sequence of positive reals, 0≤θ≤1. Then

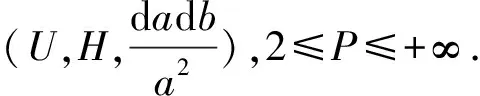
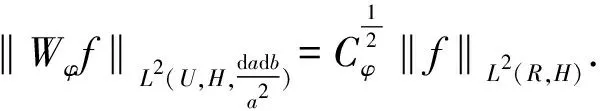
ForP=∞,

|(f

‖f1‖2‖φ1‖2+‖f2‖2‖φ2‖2+

‖f1‖2‖φ2‖2+‖f2‖2‖φ1‖2=

(‖f1‖2+‖f2‖2)(‖φ1‖2+‖φ2‖2)≤

2‖f‖L2(R,H)‖φ‖L2(R,H)(by Lemma 1).

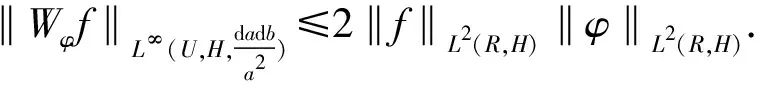
By Riesz-Thorin interpolation theorem, we obtain thatWφis of type (2,P),2≤P≤+∞.

In the following content, we define

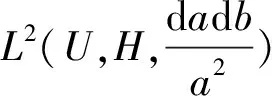
Thenτφis bounded, andτφWφis the identity onL2(R,H).

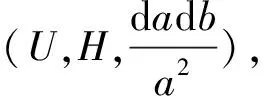
|(τφF)(x)|2=

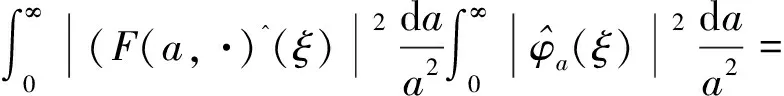
which implies

‖(τφF)(x)‖L2(R,H)=

‖(τφF)^(ξ)‖L2(R,H)≤

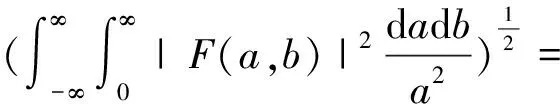
So we have

‖τφ‖≤1.

Now forL2(R,H), we can get

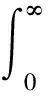
ThusτφWφis the identity onL2(R,H).

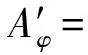
Proof Let

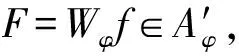
(QφF)^(a,ξ)=

Clearly,QφF=F=PφF.

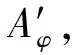
This shows

Noticing thatQφF(a,b)=(wwhere

QφF=0=PφF.

SoQφ=Pφ, we complete the proof.

Theorem 5 Forφ,Ψ∈Φand ((ξ))C(ξ) is real function,A′φis orthogonal toA′ψ, if and only if

Proof Forf,g∈L2(R,H), we have

(ξ)((g

Now we need to find an orthonormal basis forL2(0,∞).ForZ+={0,1,2…},ν>-1,m,n∈Z+,

Letφmbe functions onR, whose Fourier transforms are given by

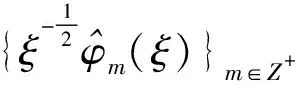
We define

H+(R,H)={f∈L2(R,H)∶supp?[0,∞)},

H-(R,H)={f∈L2(R,H)∶supp?[-∞,0)}.

Obviously,

L2(R,H)=H+(R,H)⊕H-(R,H).

We have

AW=span{φm}m≥0,

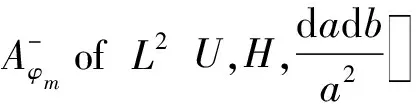
Aφm={f

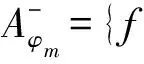
Any real wavelet functionfsatisfies Eq.(1), we have

We need only consider the following functions: Forf∈H+(R,H),

(

a

,

ξ

)=

f

(

ξ

)

g

(

a

,

ξ

)

(2)

whereg(a,ξ) is real-valued, satisfying

(3)

f(ξ) is quaternionic-valued，satisfying

Note that

(4)

Where the first equation is obtained by

(5)

the second is by

(6)

Thus by Eq.(4), we know thatt1(x) is an admissible wavelet, so

whererm∈R.Hence

By Eqs.(5) and (2), we get

So

F(a,ξ)=∑mrmWφmf(a,b)

(7)

We have a similar proof whenf∈H-.In this case, we will write the result directly,

(8)

From Formulas (7)～(8) and Theorem 5, we get

Now we give another way to prove that this orthogonal decomposition is completely decomposed.