整體規劃 分步實施

陳中峰

摘? 要：通過對課例“函數應用：停車距離問題”的賞析，闡述對中學數學建模活動的認識與看法，并就數學建模活動中“數學模型優劣的評判問題”及數學教學中學生“數學建模素養的培育問題”提出建議.

關鍵詞：數學建模活動;數學建模素養;數學模型評判

數學建模活動是基于數學思維運用模型解決實際問題的一類綜合實踐活動，是對現實問題進行數學抽象并用數學語言加以表達、用數學方法構建模型解決問題的過程，包括在實際情境中從數學的視角發現問題、提出問題，并用數學的方法分析問題、構建模型，確定參數、計算求解，檢驗結果、改進模型，最終解決實際問題. 數學建模活動是落實育人方式改革的重要載體，根據《普通高中數學課程標準（2017年版）》（以下簡稱《標準》）的要求，數學建模活動要讓學生經歷完整的解決問題的過程，培養學生數學建模素、數學運算、數學抽象等素養. 因此，整個數學建模活動不可能在一節課中完整展示. 為此，組委會規定本節課可以重點展示開題報告活動和結題交流活動.

“停車距離問題”數學建模活動課，嚴格按照組委會的相關要求，以“停車距離問題”為例，采用課題研究成果匯報的形式，讓學生結合之前所學的函數，借助信息技術手段，根據現實背景和給定的數據（數據來源于《標準》第118頁表1），分析其中的變量、常量及相互關系，明確變化的特征，構建急剎車的停車距離數學模型，再通過運算求解函數模型，利用函數模型的解說明實際問題的變化規律，實現解決問題的目的. 在這個過程中，師生共同經歷發現問題、收集數據、建立模型、計算求解、檢驗模型、解決問題等環節，展示了中學數學建模的完整過程，引導學生用數學眼光觀察世界，用數學語言表達世界，用數學思維思考世界，積累了解決實際問題的基本活動經驗.

一、本節課的優點分析

1. 合理展示，突出建模過程

本節課立足于數學活動課上進行的關于“停車距離問題”課題研究的開題報告及小組交流活動，讓三個小組的代表匯報各自的建模過程與成果，分別展示了模型假設、模型建立、模型計算、模型驗證和模型改進，獲得了解決問題的函數模型，較好地展示了數學建模的全過程. 學生的參與積極性高，過程規范、匯報流暢、條理清晰，反映了執教教師在日常教學中對學生建模思想培養的重視程度.

在學生互評環節中，執教教師組織學生以小組形式展開討論，對三種建模結果進行評價，分別從過程，結果，驗證誤差，模型優、缺點等方面進行對比，反映了學生對數學建模的掌握程度及對數學相關知識的理解水平，深化了對建模過程思維嚴謹性的認識.

2. 科學引導，深化建模認識

課堂上，執教教師對學生進行適時的科學引導，逐步深化學生對建模的認識. 例如，在展示中提出“還有其他不同的數學模型嗎”，在評價中提出“已有的三種模型的優、缺點分別是什么”，在總結中提出“回想整節課，你有哪些收獲”. 以問題為導向，科學引導學生既完善了對數學建模活動的認知，又深化了對數學建模過程、法律意識及數學運用等方面的了解，并引出了后續研究數學模型的基本方向.

3. 關注應用，揭示建模意義

本節課執教教師結合交通法規的教學，向學生滲透法律意識、安全意識教育，在課堂中融入社會主義核心價值觀教育，培養學生的法律意識. 課堂上，執教教師分別引用了《中華人民共和國道路交通安全法實施條例》和《中華人民共和國道路交通安全法》中對機動車設置警告標志距離及高速公路行車間距的規定，引導學生思考法律、法規中數據設置的依據，同學生一起挖掘發現模型的現實應用價值，讓學生體會法律、法規中數據的科學性，實現本節課內在的育人目標. 同時，在運用模型解決實際問題的過程中，也揭示了數學建模的現實意義.

此外，在各小組匯報中，還可以感受到各小組在研究過程中都能夠嫻熟地應用信息技術，特別是對Excel軟件的應用. 尤其是小組2，能借助Excel軟件模擬函數、修正函數模型. 信息技術的應用既提高了學生的實際操作能力，又為數學建模活動的有效性提供了保障，信息技術的應用與展示也成為本節課的又一亮點.

總之，本節課是一節成功的數學建模示范課，為數學建模進入課堂教學提供了一個可供參照的數學案例，起到了較好的引領示范作用.

二、關于數學建模與數學探究活動的進一步思考

數學建模與數學探究活動作為高中教學的四大主線之一，是新一輪課程改革的一個亮點. 對多數高中數學教師而言是一個新的話題，還是有許多問題值得我們進一步思考.

1. 關于模型優劣的評判問題

許多數學模型的建立，是借助對數據的分析、擬合得到的，特別是函數模型，往往是通過做出散點圖，分析散點圖的走勢，選擇函數進行擬合，從而得到函數模型. 那么，應該如何判斷這個模型的優劣呢？是不是它與這些測量數據越吻合，擬合度越高，這個模型就越好？從理論上講，對于函數模型問題，無論有多少組數據，我們總能利用牛頓插值公式，得到一個與這些數據完全“吻合”的函數. 那么這個模型是不是就是最優的模型呢？顯然不是. 因為數據的獲得是通過測量得到的，而測量往往存在誤差. 因此，“吻合度”僅僅是評判一個模型優劣的因素之一. 就本課題而言，由物理學知識可知，在剎車過程中“d”是“t”的二次函數，因此無論其他函數與這些數據的“吻合度”多高，二次函數模型才是本課題的最優模型. 評判一個模型的優劣，應該看這個模型是否能客觀地反映所要解決的問題的本質. 例如，用二次函數、三次函數刻畫“茶水最佳飲用時間”問題，無論它與測量的數據如何吻合，它們都不是適合的模型，也是這個道理.

2. 關于學生數學建模素養的培育問題

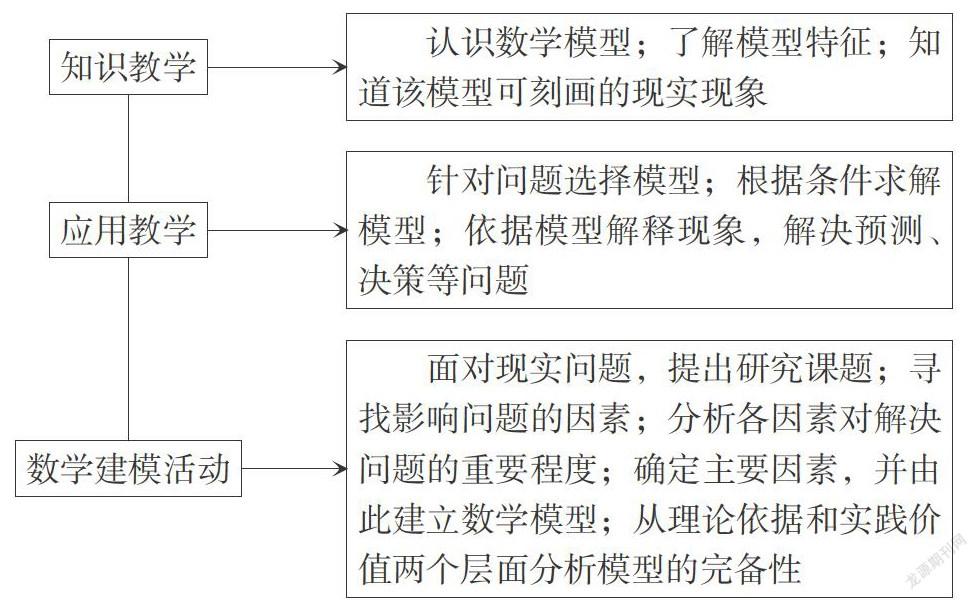
數學建模活動是利用數學知識和方法解決實際問題的應用性實踐，是學生數學建模素養的展示. 從課型的角度來講，它屬于“習作課”的范疇，僅僅是促進學生數學建模素養發展的一個環節，而不是全部. 事實上，數學建模素養的培育應貫穿數學教學的全過程，只是在不同的教學階段，其側重點也有所不同罷了，具體可用下圖表示.

對新課程的知識教學，要讓學生在理解這些知識的基礎上，根據這些知識的特點，明白這些知識反映的數學模型，明確模型的特征，知道模型可用于刻畫哪種現象. 例如，指數函數的教學不但要教給學生相關的知識，而且要讓學生理解指數函數模型的變化特點，明白指數函數可用于刻畫哪種類型的變化問題. 在習題課的知識應用教學中，要著重教授學生針對具體問題的特點，選擇合適的數學模型加以刻畫，并會根據問題給出的初始條件求解模型，根據模型解釋現象，解決預測、決策等問題. 在數學建模活動中，學生要著重解決面對現實問題如何提出切合實際的有價值的研究課題，并根據研究問題的需要尋找影響問題的因素，對問題進行理想化處理，然后根據這些主要因素建立數學模型，并從實踐和理論兩個層面分析所建立的模型的完備性，進一步優化模型.

參考文獻：

[1]中華人民共和國教育部制定. 普通高中數學課程標準（2017年版）[M]. 北京：人民教育出版社，2018.