公路平曲線加寬及其過渡方式淺析

2021-09-10 07:22:44江強興

交通科技與管理 2021年21期

江強興

摘要：本文從提高公路行車安全、減少路面病害的角度出發對公路平曲線加寬及其過渡方式提出了分車道加寬和四次拋物線過渡，雖然計算更麻煩一些但能使平曲線更加協調、順適，駕駛人員更易遵循路線行駛，提高了車輛行駛的安全性和舒適性。

關鍵詞：分車道加寬;四次拋物線;過渡方式

0 引言

汽車行駛在曲線上，前后輪會劃過不同的曲線輪跡，各輪跡半徑不同，其中以后內輪軌跡半徑最小，且偏向曲線內側，同時車輛一定轉速的前軸操縱使車身也存在一定的擺幅，故曲線內側應增加路面寬度，給車輛轉彎提供合理的空間，以確保曲線上行車的順適與安全。

根據《公路路線設計規范》二級公路、三級公路、四級公路的圓曲線半徑小于或等于 250 m時，應設置加寬。圓曲線上的路面加寬應設置在圓曲線的內側，各級公器的路面加寬后，路基也應加寬。雙車道公路在采取強制性措施實行分向行駛的路段，其圓曲線半徑較小時，內側車道的加寬值應大于外側車道的加寬值，設計時應通過計算分別確定。公路采用強制性措施實行分向行駛的比較少見，一般雙車道路面的平曲線均采用內側加寬的方式，如下圖1、圖2所示，存在著以下缺點：

（1）混凝土路面施工時按設計中線放樣，交通標線施工一般按照縱縫施工。路面雙車道的加寬值都加在曲線內側車道，內側車道就太寬造成了浪費，當采用一個板塊時增加了混凝土板應力，使路面出現縱向裂縫病害。曲線外側車道沒有加寬，滿足不了汽車行駛的寬度要求，車輛往往跨線行駛，違反了交通規則，增加了安全隱患。

（2）路面的幾何中心偏離了路線設計中線，實際路中線偏向內側，在緩圓和圓緩二點曲率不連續。

1 加寬值的方法和計算

為克服以上缺點，本文參照強制性措施實行分向行駛的路段加寬規定，提出雙車道路面平曲線加寬均實行分車道加寬，內側車道向內側加寬，外側車道向外側加寬，具體分析如下：

普通汽車行駛在曲線上如圖3、圖4所示：

當汽車行駛在曲線內側車道時：

當汽車行駛在曲線外側車道時：

式中：A——汽車后軸至前保險杠的距離（m）;

r——路中心圓曲線半徑（m）;

x——富余寬度，下列計算時以0.5 m計;

b——普通汽車的加寬值（m）。

半掛車的加寬值由圖5的幾何關系求得：

當汽車行駛在曲線內側車道時：

當汽車行駛在曲線外側車道時：

式中：A1——牽引車保險杠至第二軸的距離（m）;

A2——牽引車第二軸至后軸的距離（m）;

r——路中心圓曲線半徑（m）;

b——半掛車的加寬值（m）。

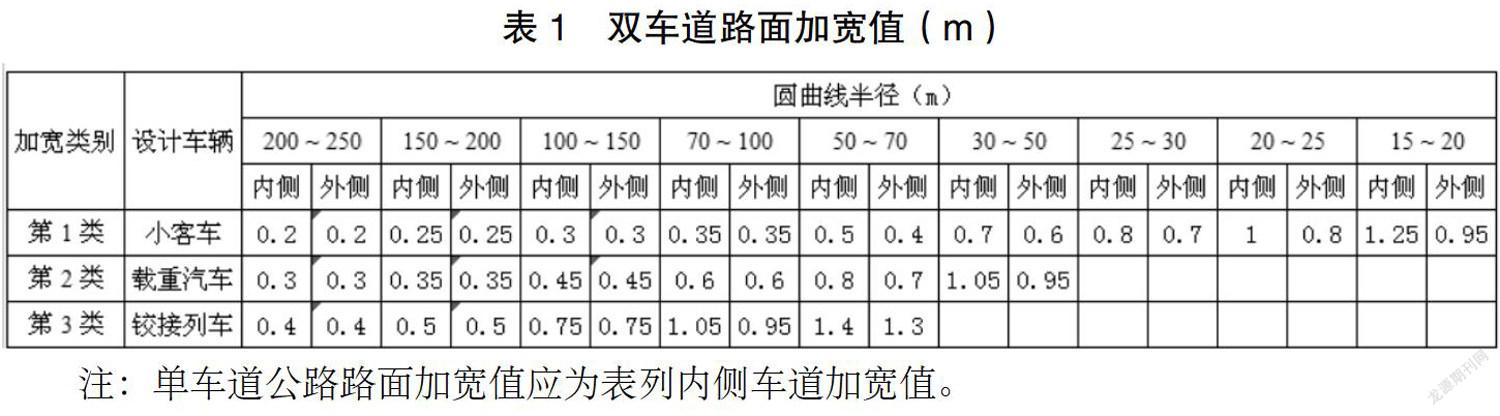
根據《公路路線設計規范》表7.6.1雙車道路面加寬值，按總加寬寬度不變，分車道加寬值計算如下：

2 加寬的過渡

根據《公路路線設計規范》規定：設置回旋線或超高過渡段時，加寬過渡段應采用與回旋線或超高過渡段長度相同的數值。

雙車道路面加寬過渡段的過渡方式主要有兩種，一種是采用長度成比例增加的比例漸變方式，一種是采用四次拋物線漸變方式，列出計算公式如下：

比例漸變方式：

四次拋物線漸變的方式：

式中：——任意樁號位置（任意點）距加寬過渡段起點的距離（m）;

——加寬過渡段的長度（m）;

b ——圓曲線上的全加寬值（m）;

——任意樁號位置（任意點）的加寬值（m）。

內側車道向內側加寬，比例過渡簡單易作，但經加寬以后的路面內側與行車軌跡不符，緩和段的起終點出現破折，于路容也不美觀;四次拋物線過渡的路面內側邊緣圓滑、美觀。外側車道加寬時是向外加寬，加寬后邊線會不會向外側凸出呢。根據回旋線切線支距法公式，曲線上該點的外側加寬值大于支距y時外側邊線向外凸出。

比例過渡：

四次拋物線過渡：

式中：——任意樁號位置（任意點）加寬值與支距y的差值（m）。

由上式可得：比例過渡當時外側車道邊線向外側凸出;四次拋物線過渡時由于公式比較復雜，較難判斷外側車道邊線是否會向外凸出，采用窮舉法進行試算，發現是否向外凸出與曲線半徑、全加寬值和回旋線長度有關，一般情況下外側車道邊線不向外凸出或凸出數值較小，不影響駕駛員正確判斷和行駛。推薦外側車道加寬過渡采用四次拋物線，為使內外一致，建議內外側均采用四次拋物線過渡。

汽車行駛在曲線上，前后輪會劃過不同的曲線輪跡，各輪跡半徑不同，其中以后內輪軌跡半徑最小，且偏向曲線內側。在雙車道路面上汽車末超車行駛時應各行其道，內側車道的汽車前保險杠外側沿路中線行駛在曲線起點處開始轉彎，其后內輪同步偏轉進入曲線，即后內輪提前A米距離進入曲線，因此內側加寬應提前A米開始加寬，A值為汽車后軸至前保險杠的距離，不通行或較少通行鉸接客車和鉸接列車可取整為10 m，通行鉸接客車和鉸接列車時可取為15 m。外側車道則相反，后內輪曲線起點處開始轉彎，汽車前保險杠已進入曲線，即汽車延遲A米才開始轉彎，與外側車道向外加寬相吻合，不需要延遲處理，考慮到外側車道延遲轉彎，建議小半徑曲線時采用較大的緩和曲線長度。

當線型為S形或C形時內側車道提前加寬后，前后二個曲線對提前加寬段都有一個加寬值;提前加寬段上任意點的加寬值如何計算，經不同線型組合試繪后，得出疊加的方法，如下式：

式中：——任意樁號位置（任意點）的總加寬值（m）。

——任意樁號位置（任意點）的前曲線加寬值（m）。

——任意樁號位置（任意點）的后曲線加寬值（m）。

3 加寬的面積

四次拋物線加寬過渡段的加寬值為四次拋物線變化，其加寬面積采用定積分計算：

求原函數：

當等于時，加寬過渡段加寬的面積：

式中：——任意樁號位置（任意點）距加寬過渡段起點的距離（m）;

——加寬過渡段的長度（m）;

b ——圓曲線上的全加寬值（m）;

——任意樁號位置（任意點）的加寬值（m）。