逆向思維在初中物理解題中的應用

湯中華

摘 要：通過運用逆向思維，初中生可以在解答物理問題的時候更活躍地探究其解答關鍵線索，迅速理性題目中不同信息之間存在的聯系，實現高效整合碎片訊息，用更方便的方法實現對于題目的求解過程.

關鍵詞：逆向思維;初中;物理;解題應用

初中生們在學習物理知識的時候，往往需要運用所學知識解決各種問題，而很多問題的解決方案相對復雜繁瑣，學生很難迅速找到解答關鍵線索.而通過運用逆向思維方式，學生們往往能夠從另一個角度進行已知條件分析，從而另辟蹊徑，順利完成解答.接下來，筆者將從多個方面簡單分析逆向思維在初中物理解題中的一些關鍵應用技巧方法，提升學生們的物理解答能力跟思維能力.

一、運動問題的逆向思維應用

跟運動相關的物理問題經常會用到逆向思維進行解答，因為對于初中生們而言，他們接觸物理這門學科的時間還不算很長，雖然有些知識都學習過了，但是在實際做題的時候，出題人一旦有所改變，將物體運動狀態進行修改，學生們就不知道該從何處下手了.而運用逆向思維能力，我們從運動狀態末端往回推導，慢慢還原到“初態”，這樣能夠更好地幫助學生理清物體所做運動的特點，也符號他們所學的知識最初形態.比如，我們將做加速運動的物體倒著看，就是一個減速運動，而作減速運動的物體按照逆向思維就變成了了加速運動，具體應用哪種方法，學生要針對題目特點以及自己的學習情況有所變通，盡可能地將復雜的物體運動過程簡化，按照自己最好理解的方式進行轉化.

例題：有一輛裝滿貨物的卡車，總重量為35000N，載著貨物以10米每秒的速度勻速行駛在水平的路面上，當卡車勻速行駛十分鐘后，已知其受到的阻力為3000N，試求在卡車行駛的十分鐘內，發動機所產生的牽引力對車作用為多少？卡車功率為多少？

我們在分析本問題的時候，如果按照常規思維進行探究，很容易就會受到卡車總重量為35000N這個數字的干擾，其實在本題目當中，并沒有用到這個數.從逆向角度出發，我們首先利用距離計算公式S=VT計算出在十分鐘內卡車行動總距離是10

m/s×60×10s=6000m.而在勻速運動下，根據“力的作用是相互的”這一定理，我們就可以很迅速推導出：卡車受到的牽引力與阻力應該是相等關系，即F=f=3000N，牽引力對卡車作用W=Fs=3000N×6000m=1.8×107J，功率P=Wt=30000W，完成解答.利用逆向思維，初中生有效規避開了題目中存在的干擾項，從所求推導已知，順利找到了牽引力、阻力、功率之間存在的必然聯系.多加鍛煉，學生們轉化思路的能力跟速度都會大大加強，準確地找到問題解決突破口提升做題效率，自我做題信心也慢慢加強.

二、磁場問題的逆向思維應用

逆向思維法就是要求寫題人從題目已經給出的條件出發一步步探索，在中間需要找到哪些條件才能滿足最后的求解問題？在解題的過程當中，我們需要不斷向自己發問：我們最終要得到怎樣的數據？在得到這樣的數據時需要怎樣的條件？如果我們已經得到了，滿足該數據的條件，那么將其當作最終結論，條件均滿足？在初中階段，雖然我們接觸到的大部分知識都是具象的生活中常見現象.但是也會存在一些我們看不見摸不著的物理現象，比如磁場，電場等等，為了探究這類物理知識，學生們更要巧妙運用物理規律之間的因果關系進行理解與學習.

圖1比如，如圖1所示，現假設在一個勻強磁場當中，我們放入一電阻不計的平行金屬導軌，導軌跟大線圈m相接，在導軌上放置裸體導線ab，要想讓m上的閉合線圈產生順時針方向感應電流，需要導線ab如何運動？

為了判斷出導線ab運動方向，可根據右手定則.這樣就可以很迅速的判斷出導線的運動狀況應該是向右運動.

三、浮力問題的逆向思維應用

在浮力問題中，最為關鍵的知識就是浮力計算公式：F浮=ρ液gV排，當物體受到浮力作用以后，如果物體本身不發生任何改變，那么在同一個g下的浮力大小自然也不會有任何改變.學生們在嘗試著解答浮力相關問題的時候，也要把握好這一知識進行逆向思維應用，盡可能地實現從反方向將最終結果的正確與否判斷出來，一步一步完成詳細答案數字的求解.

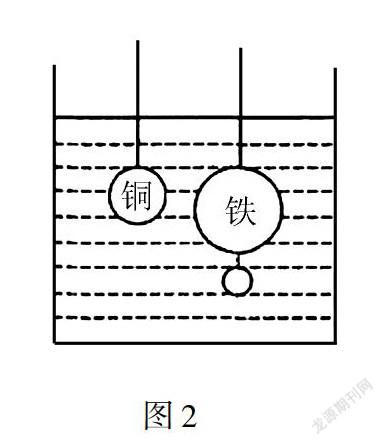
例2 現有兩個金屬實心小球，如圖2所示，分別由銅跟鐵制作而成，我們現在將這兩個小球用一個重量跟體積可忽略不計的細線系在兩個相同的測力計下面，然后將小球完全浸入水中，此時兩個測力計所顯示的數據完全相同，那么在我們將小球提出水面以后，哪個示數會更大？

本題目所描述的實驗過程還是比較清楚的，但是學生們往往不習慣這種比較兩個重新從水中拿出小球質量大小的題目，我們就可以引導學生們用逆向思維重新設計一個相反的實驗過程：假設兩個小球在提出水面以后的重量相同，那么根據浮力計算公式：F浮=ρ液gV排，體積更大的鐵球必然所收到的浮力更大一些，要想讓兩個測力計示數相同，還需要給鐵球方多加掛一些東西.故而，順勢完成了原本題目的解答：若兩個測力計所顯示的數據完全相同，那么在我們將小球提出水面以后掛有鐵球的測力計示數會更大.當我們善于運用逆向思維進行題目改裝以后，往往可以在解答一道題的時候設想出多個不同解答方法，拓展了思維的同時也能夠進一步品嘗到解答題目思考過程的樂趣所在.

四、電學問題的逆向思維應用

如果有人想要發明一種既能夠節省功，又可以節省力的機械，我們就可以告訴他這是不可能的.而為什么我們能夠迅速得出這樣的一個結論呢？這其實就是對于逆向思維最簡單而直接的應用.根據我們曾經學習過的“功的原理”，功與力的存在是相輔相成的，進而根本就不可能存在既省功又省力的新型機械.我們在解決電學問題的時候，也需要嘗試著使用逆向思維進行解答.在初中階段學生們往往都是計算在理想情況下，也就是忽略電線對于電能損耗情況的各種問題.因此，學生們在嘗試著回答問題之間，一定要從根本入手，仔細分析電路實際情況，然后找到在本題目中不會發生改變的常量.例如，在串聯電路中的電流、并聯電路中的電壓、家庭電路中的220V交流電等等，這些都是不會發生改變的常量，把握好所要求解問題與這些恒量之間的關系，再運用逆向思維，就可以很容易完成解答.

比如，當電燈的燈絲發生斷裂以后，我們再將燈絲重新接上會發現電燈泡比原先要更加明亮，這是因為什么原因的？為了回答這個問題，學生就可以試著利用逆向思維從結果入手進行分析，產生問題的根本原因是接好燈絲以后的燈泡更加明亮，那么能導致燈泡明亮的因素是因為電壓或者電流發生了改變.在家用電路中電壓已知為恒定的220V交流電，所以必然是電流增大才導致的燈泡亮度增大.我們再根據這一線索推到公式U=IR，燈絲的電阻減小了，學生很容易就可以想到了在燈絲發生斷裂以后，重新進行燈絲連接，那么燈絲長度確實是要變短，這便是電阻減小的原因.通過逆向推導，我們很順利地完成了本題解答.除此以外，學生們其實還可以從功的角度分析問題，由公式P=U2R可知，燈泡亮度變強是因為實際功率P增大的緣故，故而電阻R變小才導致了這一現象.學生們在解答實際電學問題的時候，可以采用的方法不盡相同，但是一定要在啟用逆向思維之前找好問題中存在的各種邏輯關系，這樣子才能夠順利逆向完成每一個關鍵線索的探究以及最終問題的解答.

綜上所述，在初中物理教學過程當中，教師應當在傳統教學模式之上不斷做出改進，善于引導學生用逆向思維方法分析物理問題.在初中生用常規方法解答物理問題受阻的時候，可以嘗試著從多個角度找尋題目中已經給出的關鍵因素，從未知推已知，保證物理問題求解過程始終擁有明確的目標，提升自己解題效率，增強物理知識水平.

參考文獻：

[1]王超.淺談初中物理教學中逆向思維培養[J].才智，2020（06）：148.

[2]張婭.物理教學激發學生“求異思維”之探微[J].課程教育研究，2018（02）：160.

[3]王金偉.逆向思維在初中物理教學中的應用[J].課程教育研究，2018（01）：165.

[責任編輯：李 璟]