從一道考題的多解看初中數學幾何解題能力的培養

摘 要：在各地歷年的中考數學試卷中，幾何題的份量都是很重的，大多數的壓軸題都是幾何題或與幾何相結合的綜合題.因此，加強學生幾何解題能力的培養，對提高教學質量、提升中考成績有著十分重要的意義.培養學生的幾何解題能力，要從提高對幾何基本圖形和基本結論熟悉程度、加深對定義、定理、公理、判定、性質的理解、善于發現圖中的隱含圖形、掌握基本的幾何變換和數學基本方法以及幾何證明的常見分析方法等六個方面開始.

關鍵詞：中考試題;基本圖形;基本變換;基本方法

中圖分類號：G632????? 文獻標識碼：A????? 文章編號：1008-0333（2021）02-0021-05

收稿日期：2020-10-15

作者簡介：黃江泉（1965.11-），男，廣西桂平人，大專，中學高級教師，特級教師，從事初中數學教學研究.

在2019年廣西貴港市中考的數學試題中，有下面這道題目：

已知：△ABC是等腰直角三角形，∠BAC=90°，將△ABC繞點C順時針方向旋轉得到△A′B′C，記旋轉角為α，當90°<α<180°時，作A′D⊥AC，垂足為D，A′D與B′C交于點E.

（1）如圖1，當∠CA′D=15°時，作∠A′EC的平分線EF交BC于點F.

①寫出旋轉角α的度數;

②求證：EA′+EC=EF;

（2）如圖2，在（1）的條件下，設P是直線A′D上的一個動點，連接PA，PF，若AB=2，求線段PA+PF的最小值.（結果保留根號）

這題屬于四邊形綜合題，考查了旋轉變換，全等三角形的判定和性質，相似三角形的判定和性質，三角形的三邊關系等知識，綜合性強，難度大，方法靈活，有多種不同解法.

（1）②的思路一：在EF上截取EG=EC，先證△CEG為等邊三角形，再證△CGF≌△CE A′即可.

（1）②的思路二：過C作CG∥A′D交EF于G，先證△CEG為等邊三角形，再證△CGF≌△CE A′即可.

（1）②的思路三：延長ED到G，使DG=DE，先證△CEG為等邊三角形，再證△CG A′≌△CE F即可.

（2）的思路一：連結A′F，由△CGF≌△CE A′可知CA′=CF，從而可證△A′CF為等邊三角形，進而可證A′E同時平分∠FE B′和∠F A′ B′，從而△A′EF≌△A′E B′，于是得B′與F關于A′D對稱，只要求出A B′即可.

（2）的思路二：過A′作A′M⊥B′E，得△A′ME和△A′M B′分別為含有45度和30度角的特殊直角三角形，通過計算證明B′E=EF，進而可得到B′與F關于A′D對稱，只要求出A B′即可.

（1）②的思路一、思路二用到了數學中最常用的截長法，其中思路二用到了“角平分線+平行線”得到的隱含等腰三角形，（1）②的思路三用到了數學中最常用的補短法，（2）的思路一用到了角平分線、全等三角形等基本圖形（模型），（2）的思路二用到了特殊直角三角形的基本圖形（模型），并且所有的思路中都用到了角平分線、等腰三角形、等邊三角形、直角三角形、等腰直角三角形、全等三角形等基本圖形的判定和性質.通過對本題多種解法的分析不難發現，培養和提高初中生的幾何解題能力要從以下幾方面入手：

一、熟悉幾何基本圖形和基本結論是培養幾何解題能力的前提

幾何基本圖形和基本結論是幾何知識的重要組成部分，是所有幾何解題的前提，角平分線、中線、高、點到直線的距離、動點到兩定點距離之和的最小值、等腰三角形、等邊三角形、直角三角形、等腰直角三角形、平行四邊形、矩形、菱形、正方形、垂徑定理、過圓外一點作圓的切線、全等三角形、相似三角形等基本圖形及其結論，既是考試考查的重點，也是所有解題的基本依據，我們要熟練掌握.如：

例1 （廣西貴港2016-12）如圖3，ABCD的對角線AC，BD交于點O，CE平分∠BCD交AB于點E，交BD于點F，且∠ABC=60°，AB=2BC，連接OE.下列結論：①∠ACD=30°;②SABCD=AC·BC;③OE∶AC=3∶6;④S△OCF=2S△OEF成立的個數有（? ）.

A.1個? B.2個? C.3個? D.4個

例2 （廣西貴港2017-12）如圖4，在正方形ABCD中，O是對角線AC與BD的交點，M是BC邊上的動點（點M不與B，C重合），CN⊥DM，CN與AB交于點N，連接OM，ON，MN.下列五個結論：①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2，則S△OMN的最小值是1/2，其中正確結論的個數是（? ）.

A.2? B.3? C.4? D.5

這些題目表面看起來很復雜，但實質都是考查幾何基本圖形及其結論.例1考的是角平分線、平行四邊形、等邊三角形等圖形的性質，例2考查的是相似三角形的判定和性質、全等三角形的判定與性質以及正方形的性質.只要掌握相似三角形和全等三角形的基本圖形，問題不難解決

二、理解定義、定理、公理、判定、性質是培養幾何解題能力的基礎

理解定義、定理、公理、判定、性質，就是不僅要熟記定義、定理、公理、判定、性質的結論，還要熟記定義、定理、公理、判定、性質的條件、適用范圍、注意事項等，它是幾何解題的基礎.如：

例3 （廣西貴港2019-17）如圖5，在扇形OAB中，半徑OA與OB的夾角為120°，點A與點B的距離為23，OAB恰好是一個圓錐的側面展開圖，則該圓錐的底面半徑為.

本題中，不少考生因沒有在意弧長公式中圓心角的意義，結果將120度直接代入計算，答案當然錯了.

三、善于發現圖中的隱含圖形是培養幾何解題能力的關鍵? 隱含圖形是指等腰三角形、等邊三角形、平行四邊形等特殊的圖形在整個圖形中表現出來的一部分，如“角平分線+平行線”隱含有等腰三角形，“中點+垂直”也隱含有等腰三角形，“角平分線+等腰”隱含有垂直平分，三角形含有30度和45度角則隱含可構造特殊直角三角形等等.解題中如果我們能夠充分發現這些隱含圖形，會非常有利于問題的分析和解決.如：圖6例4 （廣西貴港2019-24）如圖6，在矩形ABCD中，以BC邊為直徑作半圓O，OE⊥OA交CD邊于點E，對角線AC與半圓O的另一個交點為P，連接AE.

（1）求證：AE是半圓O的切線;

（2）若PA=2，PC=4，求AE的長.

本題中，條件出現了“中點+垂直”，隱含有等腰三角形，因而可以通過“延長AO、DC相交于M，或延長EO、AB相交于N”這樣的輔助線，幫助解決問題.例5 （廣西貴港2017-26）已知，在Rt△ABC中，∠ACB=90°，AC=4，BC=2，D是AC邊上的一個動點，將△ABD沿BD所在直線折疊，使點A落在點P處.

（1）如圖7，若點D是AC中點，連接PC.

①寫出BP，BD的長;

②求證：四邊形BCPD是平行四邊形.

（2）如圖8，若BD=AD，過點P作PH⊥BC交BC的延長線于點H，求PH的長.

本題（2）的關鍵是 “角平分型全等三角形隱含著BD是等腰三角形的高”，從而想到連結AP并延長BD交AP于E，然后過P作PF⊥AC于F 即可構造“雙垂直型相似”，利用相似列比例式即可把問題解決.

例6 （1）（廣西貴港2015-10）如圖9，已知P是⊙O外一點，Q是⊙O上的動點，線段PQ的中點為M，連接OP，OM.若⊙O的半徑為2，OP=4，則線段OM的最小值是（? ）.

A. 0 ?B. 1 ?C. 2? D. 3

（2）（廣西貴港2017-11）如圖10，在Rt△ABC中，∠ACB=90°，將△ABC繞頂點C逆時針旋轉得到△A′B′C，M是BC的中點，P是A′B′的中點，連接PM.若BC=2，∠BAC=30°，則線段PM的最大值是（? ）.A.4? B.3? C.2? D.1

上述兩題均隱含有兩邊為定長的三角形這樣的隱含圖形，因而問題實際上是“已知兩邊求第三邊的范圍”，這樣利用三角形的三邊關系即可解決.

例7 （廣西貴港2018-11）如圖11，在菱形ABCD中，AC=62，BD=6，E是BC邊的中點，P，M分別是AC，AB上的動點，連接PE，PM，則PE+PM的最小值是（? ）.

A.6?? B.33

C.26D.4.5

本題中隱含兩個最常用模型（圖形）——將軍飲馬模型和點到直線模型，因此，作E關于AC的對稱點F，過F作FM⊥AB，則FM即為所求.

四、掌握基本的幾何變換是培養幾何解題能力的橋梁

幾何變換是平面幾何的重要內容之一，是研究幾何關系的基本方法.平移、旋轉、軸對稱是初中幾何的基本變換，熟練掌握這些變換是培養和提高幾何解題能力的橋梁.

例8 （廣西貴港2018-26）如圖12，已知：A、B兩點在直線l的同一側，線段AO，BM均是直線l的垂線段，且BM在AO的右邊，AO=2BM，將BM沿直線l向右平移，在平移過程中，始終保持∠ABP=90°不變，BP邊與直線l相交于點P.

（1）當P與O重合時（如圖13所示），設點C是AO的中點，連接BC.求證：四邊形OCBM是正方形;

（2）請利用如圖13所示的情形，

求證：ABPB=OMBM;

（3）若AO=26，且當MO=2PO時，

請直接寫出AB和PB的長.

本題（2）的關鍵是進行平移變換，過B作BC⊥AO于C，即得△ABC ∽△PBM，由對應邊成比例即可;（3）的關鍵仍然是利用“雙垂直型相似”列比例式解決，只是要注意不同位置的存在，要分類討論.

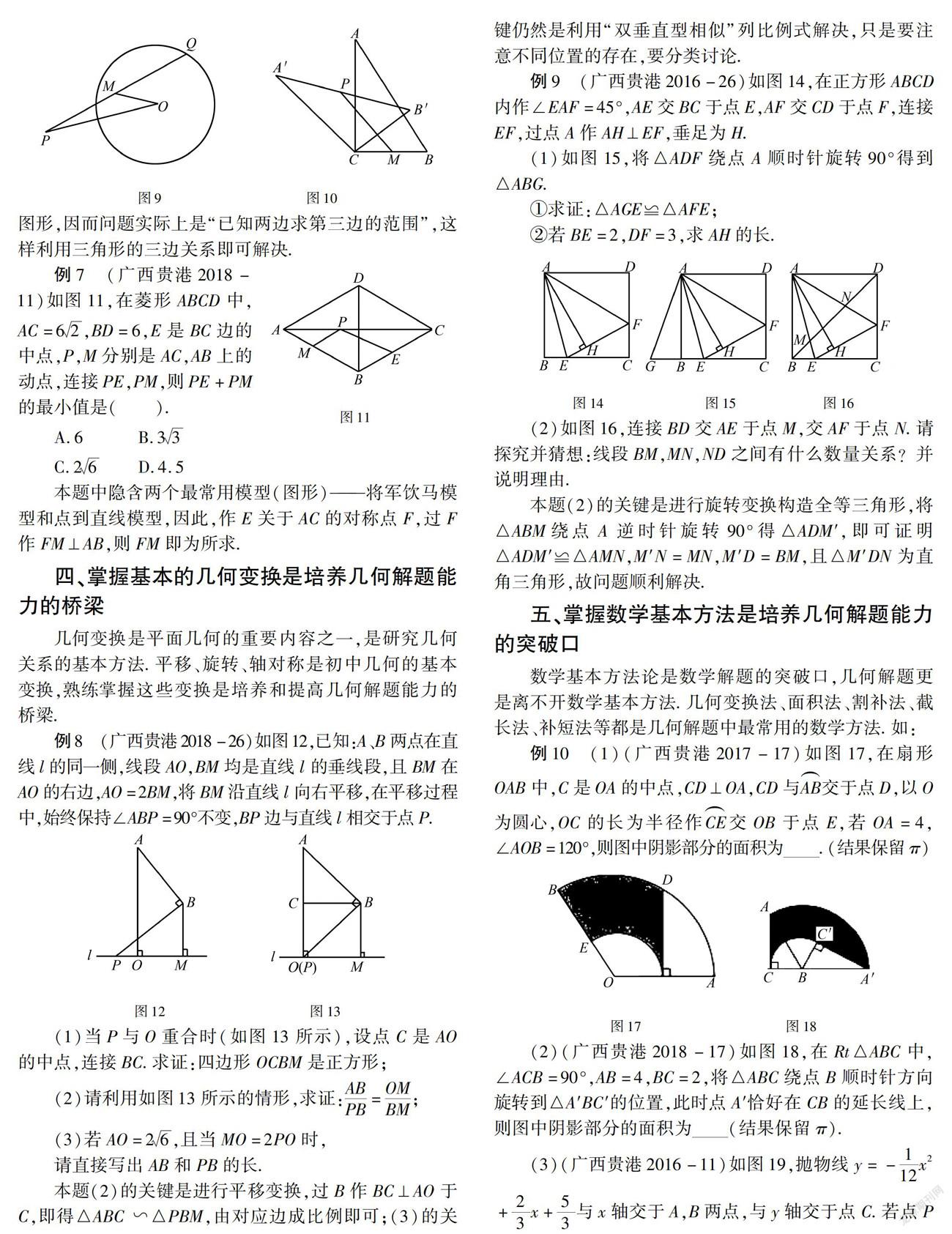
例9 （廣西貴港2016-26）如圖14，在正方形ABCD內作∠EAF=45°，AE交BC于點E，AF交CD于點F，連接EF，過點A作AH⊥EF，垂足為H.

（1）如圖15，將△ADF繞點A順時針旋轉90°得到△ABG.

①求證：△AGE≌△AFE;

②若BE=2，DF=3，求AH的長.

（2）如圖16，連接BD交AE于點M，交AF于點N.請探究并猜想：線段BM，MN，ND之間有什么數量關系？并說明理由.

本題（2）的關鍵是進行旋轉變換構造全等三角形，將△ABM繞點A逆時針旋轉90°得△ADM′，即可證明△ADM′≌△AMN，M′N=MN，M′D=BM，且△M′DN為直角三角形，故問題順利解決.

五、掌握數學基本方法是培養幾何解題能力的突破口

數學基本方法論是數學解題的突破口，幾何解題更是離不開數學基本方法.幾何變換法、面積法、割補法、截長法、補短法等都是幾何解題中最常用的數學方法.如：

例10 （1）（廣西貴港2017-17）如圖17，在扇形OAB中，C是OA的中點，CD⊥OA，CD與AB交于點D，以O為圓心，OC的長為半徑作CE交OB于點E，若OA=4，∠AOB=120°，則圖中陰影部分的面積為.（結果保留π）

（2）（廣西貴港2018-17）如圖18，在Rt△ABC中，∠ACB=90°，AB=4，BC=2，將△ABC繞點B順時針方向旋轉到△A′BC′的位置，此時點A′恰好在CB的延長線上，則圖中陰影部分的面積為（結果保留π）.

（3）（廣西貴港2016-11）如圖19，拋物線y=-

112x2+

23x+53與x軸交于A，B兩點，與y軸交于點C.若點P是線段AC上方的拋物線上一動點，當△ACP的面積取得最大值時，點P的坐標是（? ）.圖19

A.（4，3）? B.（5，3512）

C.（4，3512）D.（5，3）

這些與面積有關的問題，都要用到割補法等數學基本方法.其中（1）還要注意到圖中的隱含圖形——等邊△AOD，才能求出有關的圓心角;（2）要分割成兩個扇形和兩個三角形面積的和與差;（3）用到的是非常典型的平行軸分割的方法以及二次函數最大值的模型.

例11 （廣西貴港2019-12）如圖20，E是正方形ABCD的邊AB的中點，點H與B關于CE對稱，EH的延長線與AD交于點F，與CD的延長線交于點N，點P在AD的延長線上，作正方形DPMN，連接CP，記正方形ABCD，DPMN的面積分別為S1，S2，則下列結論錯誤的是（? ）.

A.S1+S2=CP2

B.AF=2FD

C.CD=4PD

D.cos∠HCD=35

本例可用反證法的思想，答案A明顯正確，假設B正確，很容易推導出C也正確，即B與C同對同錯，所以只能選D.

六、掌握幾何證明的常見分析方法是培養幾何解題能力的重點

幾何證明的常見分析方法很多，如綜合法、分析法、反證法、枚舉法（窮舉法）、完全歸納法、不完全歸納法……等等，但最常用的方法有綜合法、分析法和分析綜合法.熟練掌握這些常見的分析方法是我們探求解題途徑的重點和關鍵.

分析法是從求證的結論入手，以公理、定理為根據，尋求所必須的條件，再從所需條件出發，一步一步地尋求到所需的條件為已知條件時，命題即得證，這種方法也叫“執果索因”法;而綜合法是從已知條件為出發點，以公理、定理為依據，一步步推導出欲證的結論，這種方法也叫“由因導果”法;分析綜合法將分析法和綜合法結合起來，即先從結論入手看需要什么條件，再從已知出發看可導出什么結論，如果這兩者正好一致，問題即可解決，這種方法也叫“兩頭湊”的方法，通常情況下我們都用這樣的分析方法.如前面例4的（1）：

從結論（求證）入手，要證AE是半圓O的切線，就要過O作OF⊥AE于F，證OF=OB，于是要證△AOF≌△AOB，這就要證∠BAO=∠OAF（E），進而要證△ABO ∽△AOE或△ABO ∽△AFO.

再從已知出發，由∠B、∠BCD、∠AOE均為直角可得△ABO ∽△OCE，由∠AOE為直角、OF⊥AE可得△AOF ∽△AEO，由△ABO ∽△OCE得ABOC=AOOE，由△AOF ∽△AEO得AOOE=AFOF，于是ABOB=AFOF，所以△ABO ∽△AFO，這樣所需要的條件與所得到的結論就一致了，問題也就可以解決了.

這個分析問題的方法就是分析綜合法.

在培養學生幾何解題能力的過程中，除了加強學生對幾何基本圖形和基本結論的熟悉程度，對幾何定義、定理、公理、判定、性質的理解，引導學生善于發現圖中的隱含圖形，掌握好數學基本方法和基本的幾何變換以及常見的分析方法外，還要學會對幾何結論進行分類，掌握幾何難題突破的一般程序等.如對幾何結論，我們可以從線段平行、垂直、相等、不等以及角相等、不等等方面進行分類;而對幾何難題的突破，可從完善圖形（重新畫圖）、標識等量、發現隱含圖形、挖掘圖形關系（全等或相似）等方面入手.

下面通過一個具體例子來體會一下：

例12 （包頭2018-25）如圖21，在矩形ABCD中，AB=3，BC=5，E是AD上的一個動點.

（1）如圖21，連接BD，O是對角線BD的中點，連接OE.當OE=DE時，求AE的長;

（2）如圖22，連接BE，EC，過點E作EF⊥EC交AB于點F，連接CF，與BE交于點G.當BE平分∠ABC時，求BG的長;

（3）如圖23，連接EC，點H在CD上，將矩形ABCD沿直線EH折疊，折疊后點D落在EC上的點D'處，過點D′作D′N⊥AD于點N，與EH交于點M，且AE=1.

①求S△ED′MS△EMN的值;

②連接BE，△D′MH與△CBE是否相似？請說明理由.

本例中，（1）比較簡單，（2）就有難度了，如何突破呢？先標出等量：BE平分∠ABC則有∠ABE=∠CBE=45°，于是發現有隱含圖形——等腰直角△ABE，進而可得△AEF≌△DCE，從而可求得BF=1，再注意到∠CBE=45°，過G作GK⊥BC于K，則GK=BK，由相似成比例則可解決.（3）則可從折疊出發，得出相等的量有：D′H =DH，E D′=ED，D′H⊥EC等，再從所求入手，①相當于求D′MMN，而D′N∥CD，所以D′MMN=CHHD，所以，只要求出CH或HD即可.由已知可得DE= D′E=4，CD=3所以EC=5，D′C=1，設DH=x，則D′H=x，CH=3-x，由勾股定理即可求出x，問題即可解決. ②的突破則重在發現隱含圖形——等腰△D′MH和等腰△CBE（其中△D′MH為“角平分線+平行線”得出的等腰三角形，既是隱含圖形，也是典型的幾何模型），問題即可解決.

再看一例：

例13 （宜昌2018-23）在矩形ABCD中，AB=12，P是邊AB上一點，把ΔPBC沿直線PC折疊，頂點B的對應點是點G，過點B作BE⊥CG，垂足為E且在AD上，BE交PC于點F.

（1）如圖24①，若點E是AD的中點，求證：圖24

△AEB≌△DEC;

（2）如圖24②，①求證：BP=BF;

②當AD=25，且AE

③當BP=9時，求BE·EF的值.

問題（1）的思路比較具體、簡單，是一對“一線三垂直型”全等;（2）中的①只要注意到翻折隱含著角平分線，由“角平分線+平行線”即可;（2）中的 ②相當于要求PC，從何入手？只要注意到圖中含有“一線三垂直”型相似三角形，即可求得EC=20，BE=15，再注意到PG=BP=BF，用“平行”型相似（△CEF∽△CGP）即可求得BP，進而求得PC;（2）中的③則要注意到PG與BF平行且相等，連結FG即可得BPGF為平行四邊形，故GF=BP且∠EFG=∠FBP，所以△GEF ∽△EAB，由相似成比例即可解決.

當然，我們強調對數學圖形、數學結論、數學方法和幾何變換的掌握，不是簡單的把它們背下來就可以了，而是要在實際應用中去理解、去體會，學會舉一反三、觸類旁通，才能不斷形成和提高解題的能力.

參考文獻：

[1]張惠萍.初三學生解題能力突破策略[J].中學數學研究（華南師范大學版），2017（06）：30-32.

[責任編輯：李 璟]